中国股票市场效率的变迁及对市场波动性的影响
——基于Hurst指数分析法
詹奕椿
(仰恩大学 经济学院,福建 泉州362014)
资本市场的发展关乎国民经济的发展,资产市场的效率在很大程度上决定了金融作用于实体经济的效率。中国股票市场历经将近30年的变迁,其效率如何一直是国内外学者关心的问题。关于市场效率的文献数目繁多,本文基于已有研究,尝试探讨以下两方面问题:(1)市场是否有效,市场的效率是如何变动的,即研究市场效率的变迁;(2)市场效率降低是否增强了市场的波动性,即研究市场效率对市场波动的影响。
1 相关文献回顾
法玛提出了效率市场假说的三种形式:弱式、半强式及强式[1]。吕继宏、赵振全研究了涨跌停板制度对市场波动的影响,发现该制度短期会加剧市场的波动,长期有利于降低市场的波动,表明股票市场不呈弱式有效性[2]。李金林、金钰琦运用单位根检验法研究沪深两市的A股指数的日收盘价,结果表明中国A股市场为弱式有效[3]。董志勇、韩旭运用一般化资本资产定价模型研究沪深两市股票市场,结果显示市场存在羊群效应,市场无效率[4]。因此,现有文献对于中国股票市场是否有效并无定论,并且相关研究主要以某一段时间为研究对象,仅就某一段时间内作出了市场是否有效的判断。然而,中国的股票市场历经将近30年,市场每天的情况都在变动,市场的效率也随之在不断变化。从这个角度上看,前述的文献并没有回答这样一个问题:市场效率随着时间是如何变迁的,其趋势如何。
张亦春、郑振龙、林海认为,证券收益率由两部分组成,一部分是可预测的,另一部分是不可预测的。可预测的部分由无风险利率、风险大小和投资者的风险厌恶程度决定,并且随着经济周期的波动而变动[5]。由此,笔者认为:当市场有效时,市场投资者能够对可预测部分的预期收益率作出即时、一致的预期,投资者交易所引起的证券价格变动迅速地、准确地反映市场一致预期的收益率。进一步可推论,当市场无效时,投资者对证券的预期收益率存在分歧,导致证券价格变动无法准确地、迅速地体现证券内在价值的变动,由此所引发的市场博弈增强了市场的波动性,即市场效率越低,市场波动越大。
2 模型设定与估计方法及数据来源说明
2.1 模型设定与估计方法说明
2.1.1 Hurst指数
Hurst指数由英国水文学家Hurst提出并以他的名字命名(以下用“H”表示),其作为分形技术在金融量化分析领域中得到运用。H有3种形式:(1)如果H=0.5,表明时间序列可以用随机游走来描述;(2)如果0.5 本文采用R/S方法计算Hurst指数。将股票指数日收益率时间序列记为{rt},rt的计算方法为: (式1) 其中,Pt为即期市场指数价格,Pt-1为滞后一期市场指数价格,rt为市场指数收益率。 将{rt}分为A个长度为n的等长子区间。对于第a个子区间(a=1,2,…,A),计算可得: (式2) 其中,Ma为第a个区间内ru,a的平均值,Rt,a为第a个区间内第t个元素的累计离差。令极差: Ra=max(Rt,a)-min(Rt,a) (式3) 其中,若以Sa表示第a个区间的样本标准差,则可定义重标极差Ra/Sa。A个重标极差的均值为: 面向事件的中文指代语料库是在CEC的基础上,采用自动标注和人工标注的方法构建而成,以此进行事件中指代消解的研究.目前已标注完成100篇,第一期标注的语料已基本完成.本工作在已标注语料的基础上,通过对已存在要素指代、缺省要素指代和事件指代的统计,进行了初步分析,为今后的研究打下基础. (式4) 其中,子区间长度n是可变的,不同的分段情况对应着不同的(R/S)n。Hurst认为,(R/S)n与H满足以下关系: (R/S)n=KnH (式5) 对式5两边取对数可得: log(R/S)n=logK+Hlogn (式6) 式6为线性方程,因此,对log(R/S)n和logn进行最小二乘法回归分析便可以计算出H的近似值。 为求出日度Hurst指数曲线,设定Hurst指数的区间窗口为120天。为了进一步直观地分析市场效率的年度变化,本文开创性地定义年度“效率均偏指数(Mean Deviation of Efficiency Index,简记为MDEI)”。年度MDEI的计算方法如下: (式7) 其中,MDEIT表示第T年的年度效率极差,n为第T年内的交易日数量,Hurstt,i表示在第T年的第t个交易日的Hurst指数。因为市场效率线为Hurst=0.5,故,MDEIT越低表示第T年的市场效率越高,MDEIT越高表示第T年的市场效率越低。 在资本市场中,常用广义自回归条件异方差(Generalized Autoregressive Conditional Heteroscedasticity, GARCH)模型估计市场的波动。本文在研究过程中,曾以赤池信息准则(Akaike Information Criterion, AIC)最小化为选择标准建立GARCH模型,在利用样本指数收益率进行估计时,发现估计模型存在不稳定性,即方差方程的系数之和大于1。鉴于此,本文参考Parkinson(1980)的研究,用日收益极差(Range Return)作为市场波动的代理变量,其构建形式如下: (式8) 其中,PK2t为市场波动,Ht、Lt、Ot分别为t日的最高价、最低价、开盘价[6]。PK2t的分子为(ht-lt)2,不难看出,该分子隐含地反映了市场收益的振幅或者极差。根据有效市场假说,当市场有效时,市场价格能够及时、准确地反映信息,市场不存在过度交易。因此,从理论上可以说明,市场效率越高,PK2t越小(或者说日收益极差越小);市场效率越低,PK2t越大(或者说日收益极差越大)。基于以上分析,本文选择PK2t作为市场波动的代理变量。 2.1.3 线性模型 为研究市场效率对市场波动的影响,建立如下线性模型: PK2t=η+φPK2t-1+θ|Ht-0.5)|+εt (式9) 其中,PK2t为因变量;考虑到市场波动的群集特征,PK2t-1为控制变量;|Ht-1-0.5)|为解释变量。因市场效率线为H=0.5,故采用Hurst与0.5的差值的绝对值作为日度市场效率的代理变量,该值越大,市场效率越低,该值越小,市场效率越高。利用最小二乘法进行估计,预期θ的估计值为正。 利用市场指数收益率作为市场的代理变量。所用的计算市场指数收益率和Hurst指数的市场指数价格时间序列数据均来源于锐思数据库。上证综合指数(000001)的样本区间为1991年7月15日至2017年12月31日;深证成份指数(399001)的样本区间为1995年1月23日至2017年12月31日;中小板综合指数(399101)的样本区间为2005年12月1日至2017年12月31日;创业板综合指数(399102)的样本区间为2010年8月20日至2017年12月31日。每种指数均以该指数的发布日期作为样本区间的起始日期,以2017年12月31日作为截止日期。由于设定了数据窗口期,在计算MDEI时,只计算数据完整年度的MDEI。 利用样本数据得4条Hurst指数曲线(见图1)。 图1 日度Hurst曲线 观察图1可知,4条Hurst指数曲线均在数值0.6至0.8之间波动,由此可得本文的第一个结论:中国股票市场存在长期记忆性,从整体上看不具备效率。 图2 年度MDEI曲线 为进一步分析市场效率的年度变迁,利用4组市场Hurst指数时间序列数据分别计算MDEI,得出4条MDEI曲线(见图2)。 观察图2可知,4条MDEI曲线大致在0.15至0.25之间振荡波动,由此可得本文的第二个结论:市场效率随着时间的向前推移并没有显著提升。另外,结合实际发现:在2015年股票市场存在泡沫时,4条MDEI曲线同时上升,说明此时的市场效率在下降;当市场泡沫破裂之后,4条MDEI曲线同时向下,市场效率回升,曲线回归波动常态。这也为市场MDEI曲线的实用性提供了现实支撑。 利用4组MDEI时间序列数据得出的相关系数矩阵如表1所示。 表1 MDEI相关系数矩阵 由表1可知,4组MDEI的相关系数均为正,可得本文的第三个结论:中国股票各个市场的效率变动存在一定的联动性。 线性模型方程(式9)的估计结果如表2所示。 表2 线性模型估计结果 注:*、**、***表示在10%、5%和1%水平上显著。 从表2可知,4个θ的估计值均为正。其中,上证综指、深证成值及中小板综指的θ估计显著,创业板综指的θ估计值不显著。另外,φ的估计均为正且显著,说明指数收益率具有群集波动性。由此,可得本文的第四个结论:市场无效率会增强市场波动性,并且市场收益率具有群集波动性。当市场无效时,投资者对收益率的预期存在不一致性,市场存在激烈博弈且无法在短时间内达成博弈均衡,往往造成市场的过分波动。 本文以中国股票市场有效性为研究对象,通过大量的实证分析,得出了以下结论:(1)中国股票市场存在长期记忆性,整体上看不具备效率;(2)市场效率随着时间的向前推移并没有显著提升;(3)中国股票各个市场的效率变动存在一定的联动性;(4)市场无效率会增强市场波动性,并且市场收益率具有群集波动性。基于此,本文就中国股票市场的发展提出以下建议: 第一,促进机构投资者发展。中国股票市场以散户为主,容易引发羊群效应,而机构投资者的发展有利于降低市场的波动。 第二,推出切实可行的退市制度。完善的退市制度有利于加强市场竞争、降低壳资源价值以及抑制对壳资源的炒作与投机。 第三,健全股指期货交易制度。股指期货的做空机制有利于完善市场的价格发现功能,避免市场泡沫的形成。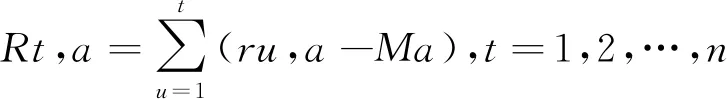
2.2 数据来源说明
3 实证检验与分析
3.1 市场效率的变迁分析

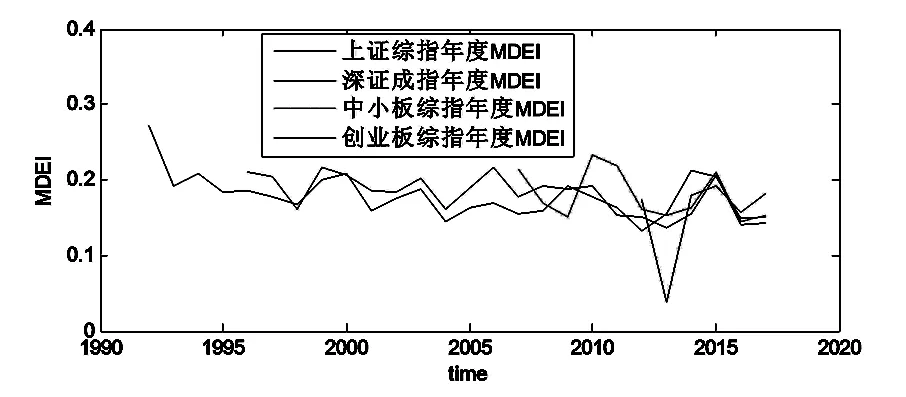

3.2 市场效率对市场波动的影响

4 结语

