颗粒尺寸对聚合釜内固-液两相流的影响
崔 锋, 董金善, 曹 宇
(南京工业大学 机械与动力工程学院, 江苏 南京 211816)
固相在液相中的悬浮操作作为工业生产中常见的工艺类型,广泛地应用于水处理、油漆及制药等行业中。利用较小的功率消耗达到理想的固相颗粒悬浮效果,可以有效降低大型聚合釜的能耗问题,提高产品的竞争力。近年来,计算流体力学(CFD)技术的发展促进了复杂搅拌器的优化设计,利用CFD技术对搅拌槽进行数值模拟,极大地解除了实验设备、实验规模、实验成本及实验周期等对研究者在两相流的混合时间预测、气液分散体系等方面研究工作的制约,因而越来越受到重视[1-4]。目前有关聚合釜固-液两相流的研究,主要集中在单层或双层搅拌器方面,而对于不同类型的搅拌桨组合下的流场研究依然匮乏[5-11]。
本文利用计算流体力学软件FLUENT对组合式搅拌器聚合釜内固-液两相流进行数值模拟,考察了在一定转速、一定体积分数下,不同固相颗粒粒径对聚合釜内固-液两相流流场及搅拌功率的影响,为实际工业生产提供一定的理论依据。
1 组合式搅拌器聚合釜模型与计算方法
1.1 聚合釜及其搅拌器结构
本文以某公司设计的30 m3聚乙烯聚合釜为研究对象,聚合釜结构简图见图1。

图1 聚合釜和搅拌桨结构示图
图1的聚合釜使用组合式搅拌器。搅拌器由搅拌轴和组合搅拌桨构成。组合搅拌桨包含3种结构的搅拌桨,分别对应图1中靠上的2个三叶翼形轴流式搅拌桨、居中的2个六半椭圆管圆盘涡轮式搅拌桨和靠下的1个三叶后掠式搅拌桨。
聚合釜中各层搅拌桨结构示意见图2。图2a中,搅拌桨直径为1 200 mm,叶片数为3,桨叶宽为400 mm,桨叶安装角度为45°。图2b中,搅拌桨直径为1 200 mm,叶片数为6,桨叶宽为220 mm,桨叶安装角度0°。图2c中,搅拌桨直径为1 200 mm,叶片数为3,桨叶宽为180 mm,桨叶安装角度为0°。

图2 各层搅拌桨结构示图
1.2 聚合釜及其搅拌桨模型
以由聚乙烯颗粒和己烷液体构成的两相流体系为研究对象。在两相流中,液相密度为600 kg/m3、动力黏度为0.000 39 Pa·s,固体颗粒的密度为950 kg/m3、粒径为0.2~0.8 mm。由于聚合釜结构较为复杂,网格划分采用非结构化四面体网格,聚合釜网格结构见图3。

图3 聚合釜网格模型
对搅拌轴、叶片等区域进行网格加密处理,搅拌桨网格模型见图4。
聚合釜及经过加密处理后搅拌桨总网格数约为220万。网格无关性检验表明,再增加网格对模拟结果已没有影响。

图4 聚合釜搅拌桨网格模型
1.3 模拟方法
应用计算流体力学软件FLUENT对聚合釜内固-液两相流场进行数值模拟。固-液两相流模拟计算采用欧拉(Euler)法,将颗粒和流体均看成连续浆液相[12-13]。此方法具有计算量小的优点,在高浓度的固-液两相流模拟中应用较为广泛。桨叶旋转区域和其他静止区域采用多重参考系法处理,湍流模型采用标准κ-ε模型,标准压力-速度耦合采用SEMPLE算法和一阶迎风差分格式。对搅拌器的搅拌轴扭矩变化情况进行监测,扭矩不再变化时表明计算收敛[14-15]。
2 聚合釜内两相流场模拟结果与分析
聚合釜内的流场分布受多种因素的影响,文中主要研究颗粒直径对聚合釜内搅拌效果的影响。采用控制变量法,模拟搅拌转速为60 r/min,固相颗粒体积分数为0.1,颗粒粒径ds分别取0.2 mm、0.5 mm、0.8 mm几种工况下聚合釜内流场的分布情况。
2.1 颗粒直径对两相流流场的影响
不同粒径条件下搅拌轴截面液相速度矢量分布见图5。由图5可知,釜内液相速度对釜内颗粒粒径的变化不敏感,不同的颗粒粒径下,液相速度分布基本一致。
不同粒径条件下搅拌轴截面固相颗粒体积分数分布见图6。由图6可知,在转速和整体固相颗粒体积分数保持不变的情况下,固相颗粒粒径越大,聚合釜内固相颗粒体积分数分布越不均匀。当颗粒粒径从0.2 mm增大到0.8 mm时,釜底最大固相颗粒体积分数从25%增大到61.6%,釜底固相颗粒沉积现象更加明显。小粒径的固相颗粒在釜内分散更为均匀,搅拌轴圆心区域和液面附近均未出现明显的分液层。

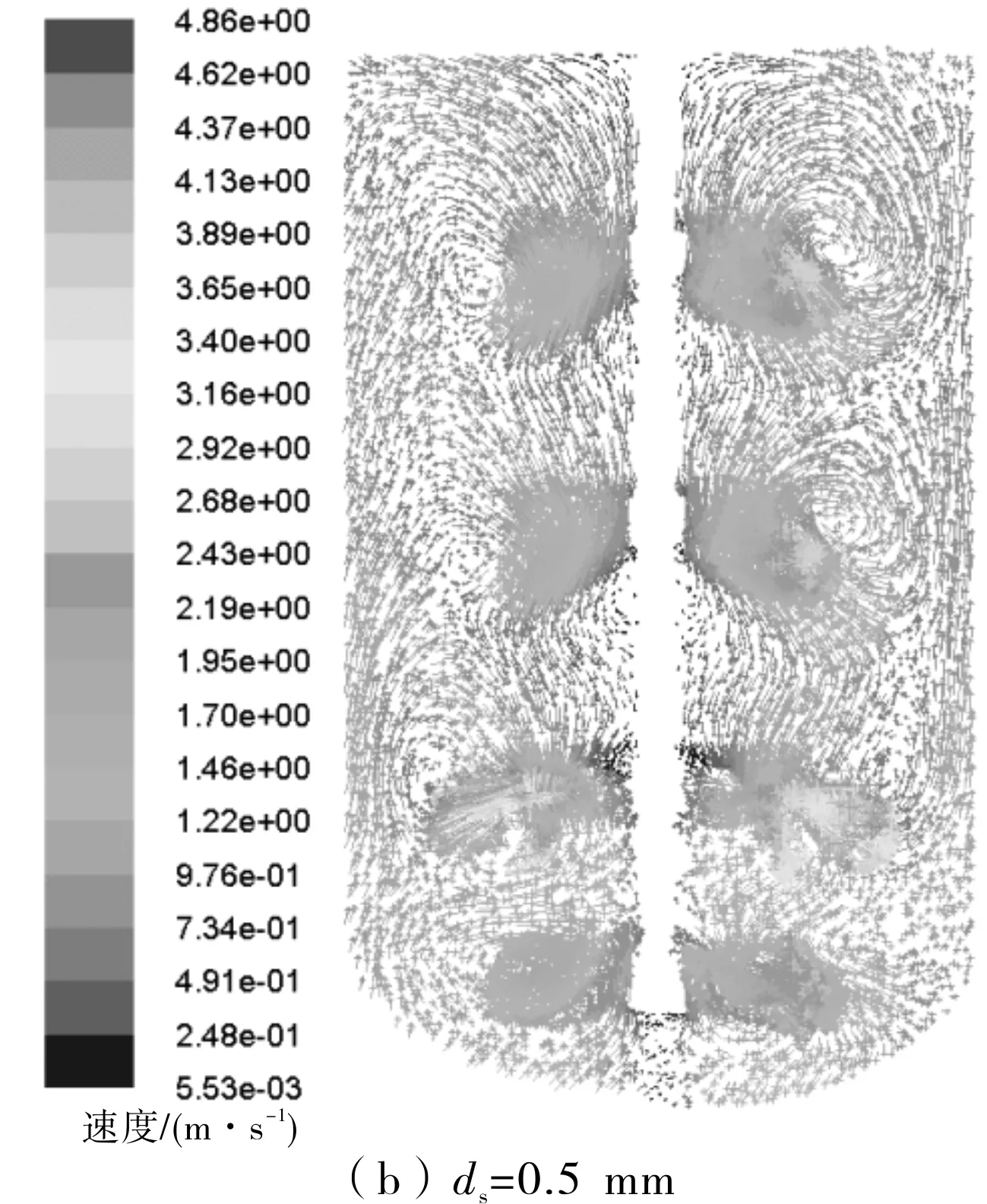

图5 不同粒径条件下搅拌轴截面液相速度矢量分布



图6 不同粒径条件下搅拌轴截面固相颗粒体积分数分布
由图6c还可知,当粒径为0.8 mm时,釜内固相颗粒分布均匀度较差,底部出现明显的固相颗粒沉积,液面附近出现明显分液层,聚合釜内混合性能较差,应该相应地提高搅拌转速,来改善釜内固相颗粒体积分数分布不均匀的情况。
为了更好地了解釜内固相颗粒的分布情况,对平行于轴线的2条线A1、A2和垂直于轴线的2条线L1、L2上固相体积分数进行分析,A1、A2、L1、L2的位置见图7。

图7 聚合釜内分析线A1、A2、L1、L2位置示图
分析线A1、A2、L1、L2固相体积分数分布见图8~图11。从图8和图9可见,颗粒粒径越小,釜内固相颗粒分布越均匀,轴向方向上固相颗粒体积分数变化趋势越平缓。粒径为0.2 mm时聚合釜内固相分布最均匀,除釜底有少量颗粒沉积外,其他区域无明显的分区现象。当颗粒粒径为0.8 mm时,釜底有大量颗粒沉积,混合性能较差,这与图6中固相颗粒体积分数分布云图基本一致。
从图10和图11可见,分析线L1处固相颗粒体积分数均随着径向距离的增大而增大,在搅拌桨顶端附近达到最大值,而后减小趋近于一定值。分析线L2处固相颗粒体积分数随着径向距离的增大而增大,聚合釜壁面处到最大值。在分析线L1处,固相颗粒粒径ds=0.8 mm时,固相颗粒体积分数由2%逐渐增大到12%,变化较大;而固相粒径ds=0.2 mm时,固相颗粒体积分数由8%逐渐增大到12%,变化趋势较为平缓。在分析线L2处,固体颗粒粒径ds=0.2 mm时固体颗粒体积分数最小值约为颗粒粒径ds=0.8 mm时固体颗粒体积分数最小值的7倍,最大值约为其2倍,表明大粒径不利于釜内固相颗粒的悬浮。

图8 聚合釜内分析线A1轴向固相颗粒体积分数分布

图9 聚合釜内分析线A2轴向固相颗粒体积分数分布

图10 聚合釜内分析线L1径向固相颗粒体积分数分布
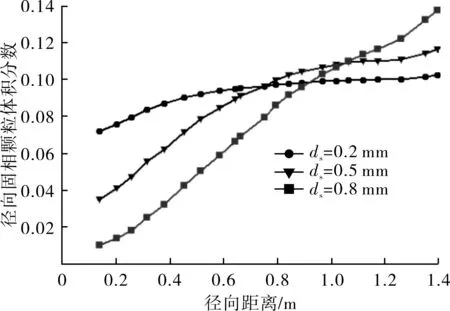
图11 聚合釜内分析线L2径向固相颗粒体积分数分布
2.2 颗粒粒径对功率的影响
由CFD得出的不同固相颗粒粒径下聚合釜内搅拌扭矩见表1,由搅拌扭矩计算得到的搅拌功率见表2。

表1 不同颗粒粒径下聚合釜内搅拌扭矩 N·m

表2 不同颗粒粒径下聚合釜内搅拌功率 kW
分析表1和表2中数据绘制的聚合釜搅拌功率在不同颗粒粒径下随着转速的变化曲线见图12。
由表1、表2和图12可知,随着釜内固相颗粒粒径的增大,功率消耗也随之增大,固相颗粒粒径ds=0.8 mm时,功率消耗最大。当颗粒粒径由0.2 mm增大到0.5 mm时,釜内搅拌功率随着颗粒粒径增大变化较大,粒径由0.5 mm增大到0.8 mm时,搅拌功率增大不显著。
3 结语
利用CFD软件对聚合釜内的流场特性进行了数值模拟。模拟结果综合分析表明,①颗粒粒径的变化对釜内液相速度的影响基本可以忽略,对釜内颗粒体积分数的分布影响显著,颗粒粒径越大,釜底颗粒沉积现象愈明显。②随着颗粒粒径的增大,组合式搅拌器的搅拌功率也增大。当颗粒粒径由0.2 mm增大到0.5 mm时,釜内搅拌功率随着颗粒粒径增大变化较大,粒径由0.5 mm增大到0.8 mm时,搅拌功率增大不显著。
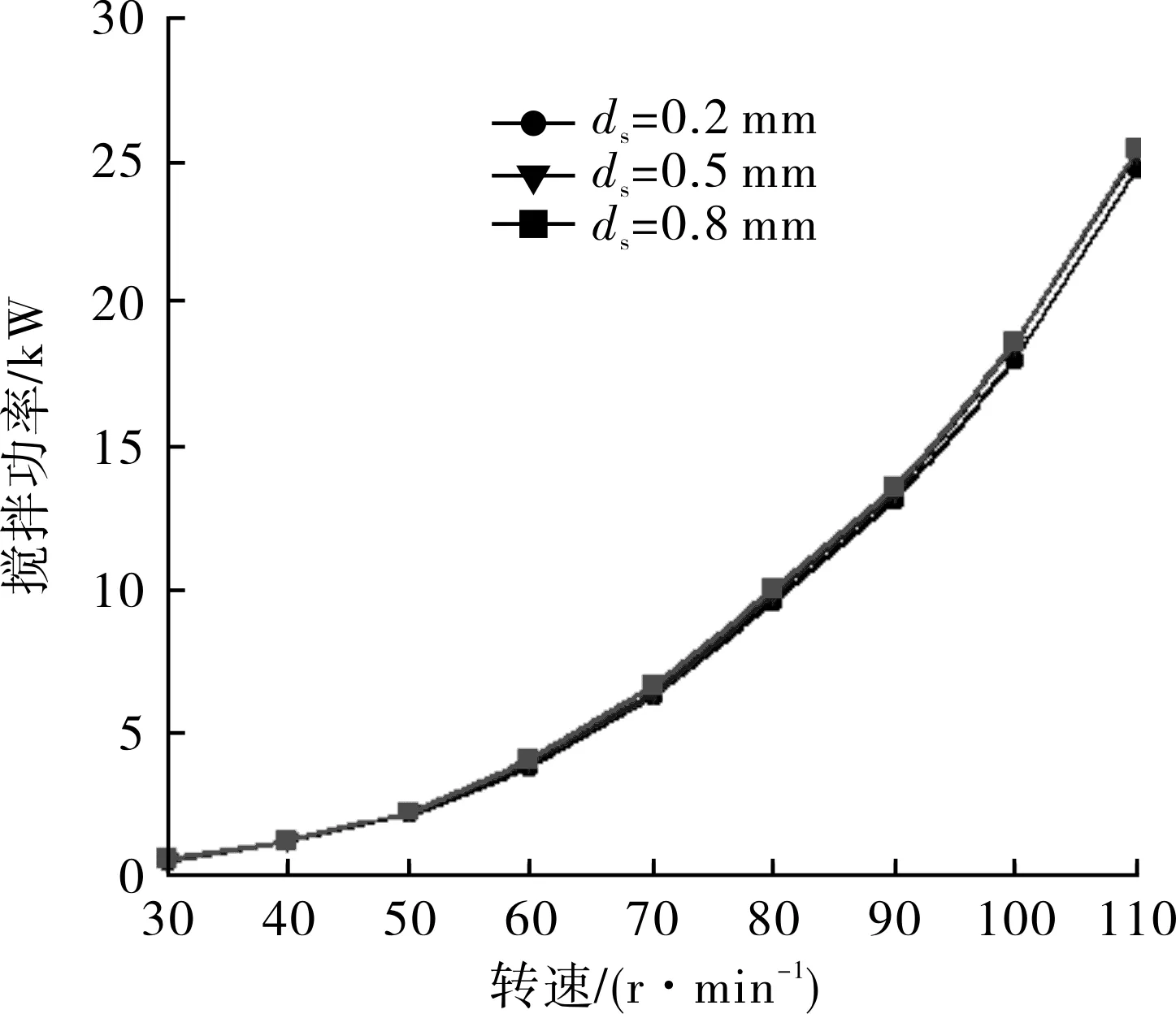
图12 不同颗粒粒径下聚合釜搅拌功率与转速关系曲线

