多个相关二分类共同终点临床试验样本量估计方法*
杨嘉莹 王诗远 李贵凡 刘 沛△
1.东南大学公共卫生学院卫生统计学系(210009) 2.北京民海生物科技有限公司
对于具有多个主要终点(multiple primary endpoints)的临床试验,当规定任一个终点成功整个研究即为成功时,可称为并交(union-intersection)试验[1],此类研究常常会带来多重性问题。与之相反,针对多个共同终点(multiple co-primary endpoints)的临床研究称为交并(intersection-union)试验[2-3],一般规定多个终点同时具有统计学意义时整个试验才记为成功。这种设计避免了多重检验所带来的Ⅰ类错误膨胀,但需要对Ⅱ类错误进行调整,为临床试验样本量计算带来了新挑战[4-6]。当试验结局为连续型终点时,已有文献对样本量估计方法进行探讨[7],而当试验结局为二分类终点时,相关研究较少且存在一些不足。在实际工作中,由于缺少方法学支持,一些研究者将各终点计算所得的最大样本量作为整个研究的样本量,该方法在各终点独立时会成倍损耗全局功效[8]。另一种较常用的方法是使用Bonferroni调整法对Ⅱ类错误进行调整,但该方法过于保守,可能过多的估计样本量[9]。Song等人[10]提出了终点为率差时非劣效试验样本量计算方法,但未探讨通过各终点率差之间的相关性估计结局统计量之间相关性存在的限制。此外,基于检验统计量的联合概率模型[11]推导的样本量计算公式要求使用者具备一定的数学和计算机编程知识,这也限制了其使用。
近年来,可同时预防多种细菌或病毒亚型的多价疫苗日渐增多,如北京民海生物科技有限公司研制的多价肺炎疫苗,其研究终点可多达23个,且各终点间存在正相关,这对样本量估计提出了新的挑战。对于连续型终点研究,一种基于“膨胀因子”的方法[9]已在多共同终点临床试验中得到较好应用。虽然该方法仅适用于7个及以下终点的临床研究,但其原理可推广至二分类终点问题。本研究将针对多价疫苗发展的实际,运用随机模拟方法探讨基于Ⅱ类错误调整的“膨胀因子”方法用于二分类终点样本含量估计的合理性,并通过反推法将该方法扩展至20个终点的多价疫苗临床试验中。
原理和方法
1.单个终点样本量计算
考虑一项以率为结局的两组平行对照设计非劣效试验,可采用下述公式[12]进行样本量估计。
(1)
其中下标T代表试验组,C代表对照组;Z1-α和Z1-β分别对应一类错误率α,二类错误率β的正态分布分位数;π代表相应组别的率;d代表非劣效界值。
2.名义错误水平调整
交并试验存在Ⅱ类错误膨胀问题,在并交试验中也存在Ⅰ类错误膨胀所带来的多重性问题。一些研究者针对多重性问题提出了名义Ⅰ类错误水平调整方法,这些方法的思想同样适用于名义Ⅱ类错误水平调整。
对于具有K(≥2)个相关终点的临床试验,Tukey 等人[13]建议调整第k个假设检验的名义Ⅰ类错误水平为:
(2)
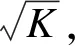
αk=1-(1-α)1/mk
(3)
其中,mk=K1-rk,若令rjk是第j个和第k个终点的相关系数,则
(4)
当各终点相互独立时,该调整方法相当于Bonferroni检验,当各终点间相关系数均为1时,该方法计算的P值相当于未调整前的P值。当各终点间平均相关系数为0.5时,该方法相当于公式(2)。尽管存在上述优点,Sankoh的研究发现该方法对α的保护水平随着终点数量的增加而下降,并提出对名义Ⅰ类错误水平增加因子c以改进整体效果,即在公式(3)中使用α’=cα替换原公式中的α。改进后的公式为:
αk=1-(1-cα)1/mk
(5)
Sankoh提供了在不同终点数和终点间相关性的情景下因子c的参考取值[16]。此类调整方法可以考虑终点之间的相关信息且无需任何分布假设。
3.改进的膨胀因子法
考虑一项具有K个终点的交并试验,当试验组和对照组间效应量相等时,各终点所需的样本量相同。以该样本量作为整个研究的样本量必然带来Ⅱ类错误的膨胀。为了达到预期的全局功效,单个研究的名义Ⅱ类错误水平应向下调整。又由于各终点间相关性差异较小,可假设各终点间具有相等且恒定的相关性,进而对计算公式简化。在公式(4)的基础上,Julious将其扩展并应用于名义Ⅱ类错误水平的调整:
(6)
其中,t=K1-ρ,K是共同终点数,ρ是各终点间的相关系数,β是名义II型错误水平。将公式(6)计算得到的βK代入公式(1),可得调整后的样本含量。膨胀因子(inflation factor,IF)则为调整后的样本含量与未调整样本含量的比值,即:
(7)
公式(6)中不同相关性和终点数目时因子c的取值详见Sankoh及Julious文献[9,16]。由已给出因子c的值可知,在相同终点个数下,该参数取值可近似于随相关系数增加而减少的直线,因此可采取插值法,参照10个终点下相关性为0.5和0.7水平下的结果补齐相关性为0.6时的因子c取值。
4.通过膨胀因子反推因子c
通过模拟试验,我们可以得到各情景下为了达到80%全局功效所需样本量。该样本量与通过公式(1)计算所得样本量的比值即为IF。通过公式(7),我们可知Z1-βK的计算公式为:
(8)
(9)
其中F(1-βK)为1-βK在标准正态分布下的累积分布函数。通过公式(8)及公式(9),我们可以计算得到βK的结果,结合公式(6)即得:
(10)
通过对因子c的反推,我们可以利用模拟方法获取20个共同终点情景下的膨胀因子,进一步补充因子c的取值,从而满足多价疫苗临床试验样本量计算的需求。
模拟试验设计
以一项具有K(≥2)个终点的非劣效疫苗临床试验为例,结局指标为抗体阳转率。试验组和对照组的样本量相同,分别用nT和nC表示;第i(i=1…K)个终点各组的阳转率分别用πTi和πCi表示;假设K个终点间的相关性相同,各组终点间平均相关性分别用ρT和ρC表示。受试者各个终点阳转率的综合反应向量,Yj=(Yj1,…YjK)T(j=1…n)服从E[Y]=πT,var[Y]=πT(1-πT)的K变量伯努利分布。由于该研究的主要目的是探讨在各终点间具有相关性的情况下,膨胀因子法用于多个终点交并试验样本量计算的效果,当试验组和对照组的组间效应存在差别时,该差别会主导样本量计算,削弱相关性的影响,因此本研究仅考虑πTi=πCi,ρT=ρC的情况,模拟试验通过SAS 9.4实现。
结论:总的来说,在日常使用pH计的过程中,一定要注重细节,规范程序,区分不同类型,注意pH计相关的校准和温度补偿等环节。
1.模拟方法
基于以上假设,该研究根据不同参数情景对各样本量对应的全局功效进行蒙特卡洛模拟。初始样本量通过公式(1)计算所得单个终点所需样本量,终止样本量采用Bonferroni调整的样本量(βK=β/K)。具体步骤如下:
(1)根据均值πTi,πCi和终点间相关系数ρT,ρC分别为试验组和对照组的n例受试者产生K对服从伯努利分布的原始数据。
(2)组间阳转率采用95%CI法进行非劣效性检验,分别计算试验组与对照组组率差的95%置信区间下限并与非劣效界值比较。
(3)若K个共同终点同时满足非劣效要求,则将该试验计为“成功”,否则计为“失败”。
(4)重复1-3步骤1000次,统计“成功”次数计为m,则在该样本量下试验的全局功效为m/1000。
(5)增加样本量,并重复步骤1-4,直至达到终止样本量。
2.参数设计
模拟试验中各参数取值见表1。结合疫苗临床试验的实际数据,终点个数考虑了四种情景,阳转率考虑了五种情景,相关系数考虑了四种情景,合计80种组合情景。分别模拟各情景下全局功效随样本量增加的变化,并以模拟结果作为参考,评价“膨胀因子”法用于各情景下二分类共同终点研究样本量计算的效果。拟采取的评价标准如下:
标准1:“膨胀因子”计算的样本量不小于模拟结果。
标准2:“膨胀因子”计算的样本量与模拟结果差异在模拟结果的5%以内。
标准3:“膨胀因子”计算的样本量与模拟结果差异在模拟结果的10%以内。
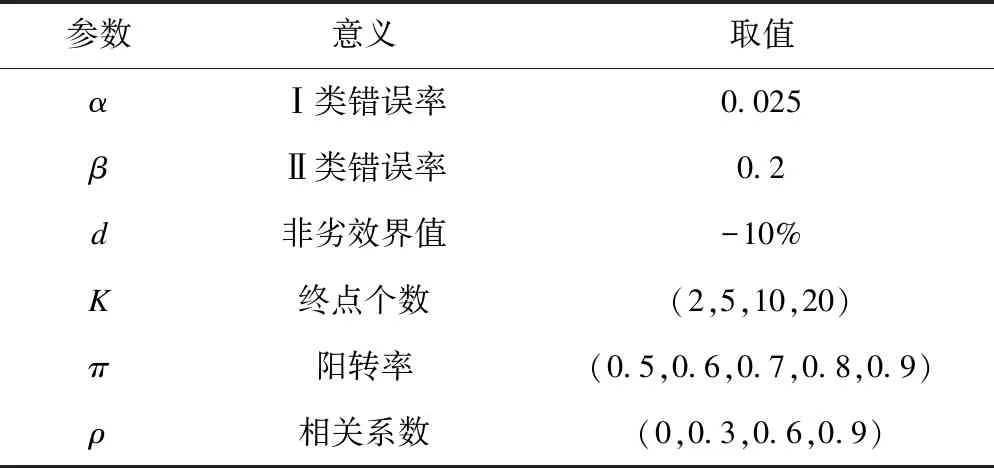
表1 模拟试验参数及取值
同时满足标准1和标准2,则认为该情景下“膨胀因子”法效果较好,满足标准3为效果适中,否则为效果较差。
结果
1.全局功效变化
以样本量为横轴,全局功效为纵轴,2、5、10和20个终点下不同阳转率及相关性组合的全局功效变化曲线见图1。
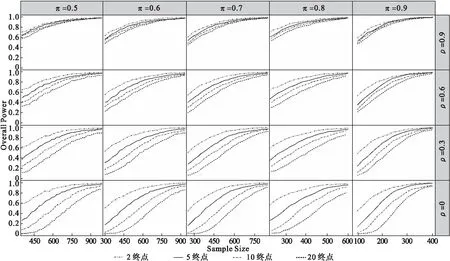
图1 多个共同终点在不同相关性,阳转率下全局功效随样本量增加的变化
图1的模拟结果显示:
(1)为达到预订的全局功效水平,共同终点的数目越多,所需样本量越大。如ρ=0,π=0.5时,为达到80%的全局功效,2、5、10及20个共同终点分别需要515、663,784及903例受试者。
(2)同一阳转率水平下,为达到预计全局功效水平,各终点间相互独立时不同终点间所需样本量差距最大。随着相关性的增加不同终点的全局功效曲线趋近,即不同终点所需样本量的差距缩小。如为达到80%的全局功效,π=0.5,ρ=0时20个终点比2个终点所需样本量多388例,而π=0.5,ρ=0.9时,20个终点比2个终点所需样本量仅多100例。
(3)同一相关性水平下,不同阳转率水平的全局功效曲线相似。如ρ=0时,2、5、10及20个终点的全局功效变化趋势相似。
2.“膨胀因子”法效果评价
Julious提供了7个及以下终点时因子c的取值[9],Sankoh文献中提及10个终点时部分情景下因子c的值[16],我们通过插值法补齐因子c的取值,并计算在本次模拟情景中2个、5个或10个共同终点时“膨胀因子”法得到的样本量,与模拟结果比较并根据上文提到的3条标准进行评价。
由表2可知,在2个终点时,除π= 0.9且ρ= 0.9情景外,“膨胀因子”法计算结果与模拟结果差异均不超过±5%;特别的,当ρ= 0.6时“膨胀因子”法效果较好;在5个终点时,除ρ= 0.9的情景外“膨胀因子”法效果适中,特别的,当ρ= 0或ρ= 0.3时,绝大多数情景下“膨胀因子”法效果较好;在存在10个共同终点的研究中,除ρ= 0.9的情景外“膨胀因子”法效果适中。
3.不同情景下的膨胀因子及参数c取值
由上可知,在ρ= 0.9时,“膨胀因子”法用于样本量计算的效果并不理想。为了改善该方法的效果,我们利用模拟得到的膨胀因子反推因子c的取值,并进一步扩展到20个共同终点的情景中。结果见表3。

表2 膨胀因子”法样本量计算结果与模拟结果比较
*:差异=(计算结果-模拟结果)/模拟结果;加粗数据表示结果较好;黑框数据表示结果较差。

表3 各情景下膨胀因子及因子c取值
由表3可知不同终点数及终点间相关性组合下使用“膨胀因子”法计算样本含量时因子c的取值。其中加粗数值由Sankoh及Julious文献提供,其他结果通过公式(8)计算。由表3中提供膨胀因子可知,各终点间相关性越高,为达到预先设计的全局功效,所需样本量膨胀因子越小。特别的,当各终点相互独立(ρ= 0)时,因子c取值为1,公式(6)可进一步简化为:
(11)
公式(11)即为Sidak调整公式[17]。
讨论
存在多个共同终点临床试验的样本量计算问题已经引起国内外研究者的注意,但传统计算方法仍存在较多问题。各终点分别计算样本量并取其最大值的方法在各终点间效应量相似时会明显低估样本量,造成整个研究的全局功效达不到预期;而通过Bonferroni调整的方法又过于保守,往往高估样本量,造成人力物力的浪费。Sankoh提出的对名义错误水平调整的程序相对宽松,而由Julious改进后的“膨胀因子”方法宽松程度介于Sankoh方法与Bonferroni调整方法之间。此外,“膨胀因子”法不依赖于特定的研究假设和检验方法,为多终点问题提供了通用的样本量计算方法。
总的来说,“膨胀因子”法可以均衡相关性对多个共同终点临床研究样本量计算的影响。存在2个共同终点研究中,“膨胀因子”法效果较好;存在5~10个共同终点的研究中,当终点间相关性小于等于0.6时,“膨胀因子”法效果适中。实际临床数据各终点间往往存在一定的正相关,相关性可低至0.2高至0.8。对于多终点临床研究,终点间相关性的存在可以节约样本量,忽略这种相关性则会造成样本量的高估。而在另一些情况中,临床试验中各终点是相互独立的,“膨胀因子”法近似于Bonferroni调整法。
本文提供了存在2、5、10、20个二分类共同终点时样本量的膨胀系数,出于保守性的考虑,介于上述终点数之间的研究可向右选择相近终点数对应的膨胀因子。超过20个终点的研究样本量建议通过模拟推算。此外,本研究关注试验组与对照组二分类指标水平相同的情况,在试验组与对照组的效应量不同的情况下“膨胀因子”法可能无法满足样本量计算需求,一些根据各组效应量差别为各终点分配不同研究功效从而达到全局功效的样本量计算方法为类似情况提供了解决办法[18]。
综上,本文通过蒙特卡洛模拟研究了“膨胀因子”法用于多个二分类共同终点临床试验样本量计算的合理性,修改了相关性较高时因子c的取值,并进一步扩展至20个共同终点的情况。

