犁体曲面离散元仿真试验与参数优化

何永强，贺俊林，杨作梅

(山西农业大学 工学院，山西 太谷 030801)

0 引言

我国是一个农业大国，耕地面积大，达1.35×108hm2[1],普遍使用铧式犁耕作，存在犁体阻力大、耗能高的问题[2]。近年来，随着电动拖拉机的发展与应用[3]，在保证铧式犁耕作质量的情况下，节能更是一种必然趋势。为减小犁体阻力，降低能耗，本文运用离散元法对犁体曲面进行仿真优化试验。

离散元法(Distinct Element Method, DEM)是用来计算散体介质系统(干散体、湿散体或两相悬浮体)中不连续问题力学行为的一种数值模拟方法[4]，可以通过单元间多种连接方式来体现土壤等多相介质间的不同物理关系，从而有效地模拟土壤的开裂、分离等非连续现象及工作部件与土壤颗粒模型间的相互作用力[5]。张青松等[6]利用离散元法对油菜直播机开沟犁进行了优化与试验，犁体牵引阻力比优化前减小了11.26%。Tsuji[7]等利用离散元法模拟了推土机铲板对土壤的开挖和推进过程，得到了土壤颗粒滚动、间歇性坍塌等运动特征。目前，对犁体曲面优化方面的研究主要运用解析法[8]、有限元[9-11]等方法，取得了一定的成果，但对利用离散元仿真试验优化方面的研究鲜见报道。

为减小犁体耕作阻力，笔者建立了EDEM离散元土壤仿真模型，对不同犁体曲面参数的铧式犁耕作过程进行仿真，得出犁体阻力动态变化趋势和最佳的犁体结构参数组合，为犁体的优化提供一种离散元分析方法，且为铧式犁的优化设计提供参考。

1 犁体曲面设计

为减小犁体阻力，以北方系列BT-30扭柱型熟地犁为例，针对其耕作阻力大、耗能高的问题，参照GB/T14225-2008，设计犁体幅宽b为300mm、最大耕深a为250mm。

1.1 导曲线的绘制

导曲线是确定水平直元线位置的引导曲线，扭柱型犁体曲面大多采用抛物线状的导曲线。本文中导曲线的直线部分长度S根据耕深取50mm，导曲线的抛物线部分采用包络线作图法[12-14]绘制，如图1所示。导曲线开度l、导曲线高度h、端点切线夹角ω分别为

l=C1b(cosΔε-sinε)

(1)

(2)

(3)

其中，l为导曲线开度；C1为常数；b为幅宽；Δε为导曲线扣垡角；ε为犁铲安装角；h为导曲线高度；ω为端点切线夹角。

为了提高犁体碎土能力，减小犁铧与沟底土壤的摩擦、降低犁体损耗，一般ε的范围为25°～30°。导曲线扣垡角Δε一般在5°～10°之间，Δε越大扣垡作用越强，可以改善碎土性能，但阻力随之会增大。C1为常数，一般在1.0～1.7之间。取小值时，碎土作用较强，但翻垡的效果减弱且阻力增大。为了保证耕作质量，本文取C1=1.3。

图1 导曲线

1.2 元线角变化规律

熟地型犁体曲面元线角变化规律分为两部分，元线角θ0～θmin的变化规律一般采用直线，所以按照直线法求出各元线角即可。元线角θmin～θmax一般的变化规律为二次曲线的一部分，方程为

(4)

式中x—笛卡尔坐标系中二次曲线的横坐标；

y—笛卡尔坐标系中二次曲线的纵坐标。

为了方便计算，现将直线部分和二次曲线部分上元线角的变化统一表达为元线角与对应元线号的函数关系，即

(5)

式中θn—元线号为n时的元线角；

θ0—初始元线角(即铧刃角)，一般取θ0=36°～45°；

n—元线号；

nmin—最小元线号，nmin=0；

nmax—最大元线号，nmax=15；

θmin—最小元线角，θmin=40°；

θmax—最大元线角；θmax=47°；

Δz—元线之间的距离,Δz=25mm。

1.3 三维模型的建立

利用SolidWorks软件建立犁体三维模型。首先，选择参考平面分别绘制出铧刃线和导曲线草图；然后，根据元线号和与其对应的元线角绘制水平直元线，并利用“边界-曲面”命令生成光滑的曲面； 最后，绘制出犁体曲面前视图，将犁体曲面前视图投影到初始光滑曲面上，得到一个封闭的空间曲线。在此基础上，利用“裁剪-曲面”命令将犁体曲面裁剪出来，再使用“加厚”命令将犁体曲面变为三维实体，结果如图2所示。

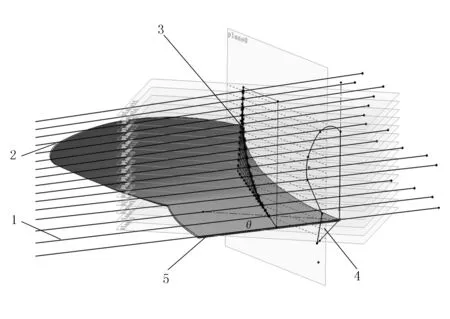
1.水平直元线 2.犁体实体模型 3.导曲线 4.犁体曲面前视图 5.铧刃线。

2 仿真模型的建立

2.1 土壤颗粒间接触模型

土壤颗粒之间具有一定的黏结作用，故采用Hertz-Mindlin黏结接触模型[15-16]。当颗粒在某时刻被黏结起来时，按照此模型计算可以得到颗粒之间法向和切向黏结力分别为Fn、Ft，法向和切向黏结力矩分别为Tn、Tt，每个颗粒法向和切向的角速度分别为ωn、ωt，每个颗粒法向和切向的速度分别为vn、vt。其中，Fn、Ft、Tn、Tt随着时步δt从0开始增加。各物理量之间的关系方程为

(6)

式中RB—颗粒间的黏结半径；

Sn—法向刚度；

St—切向刚度；

t—时间。

此模型可以阻止颗粒间切向和法向的相对运动。当法向和切向应力超过定义的临界值时，黏结关系就会被破坏，颗粒间法向和切向应力临界值满足的关系式为

(7)

式中σmax—法向黏结力定义临界值；

τmax—切向黏结力定义临界值。

为了在数学模型上体现颗粒之间的自然接触关系，接触半径应该设置大于自然中粒子实际接触半径。

2.2 离散元模型的建立

在EDEM软件中定义土壤和犁体材料属性，并设置土壤颗粒半径；然后将犁体三维模型转化为IGS格式导入EDEM软件中，赋予其犁体材料属性。设置犁体与土壤颗粒、土壤颗粒与土壤颗粒之间的相互作用的参数；然后由颗粒工厂生成土壤颗粒，设置犁体运动速度；最后，进行仿真试验研究。仿真模型如图3所示，参数设置如表1所示。

1.犁体 2.土壤

参数单位数值犁体密度ρkg/m37800犁体剪切模量GPa7.0×1010

续表1

3 仿真试验与结果分析

3.1 正交试验设计

根据水平直元线法原理和式(1)～式(5)中各参数之间的关系可知：导曲线铧刃角、犁铲安装角和导曲线扣垄角不同，犁体曲面形状就不同，可能对犁体阻力有较大影响。

为减小犁体阻力，分析了不同犁体曲面参数对犁体阻力的影响。以耕作稳定时犁体所受阻力平均值Y为试验指标，选取铧刃角θ0、犁铲安装角ε、导曲线扣垡角Δε为试验因素，运用EDEM软件进行L9(34)正交试验。为了保证犁体对土壤的滑切作用，减小犁体阻力，参照文中1.1、1.2节对以上三因素进行水平选取，如表2所示。仿真试验中，犁体作业速度设为5km/h、耕深220mm，每组试验重复3次，取平均值。

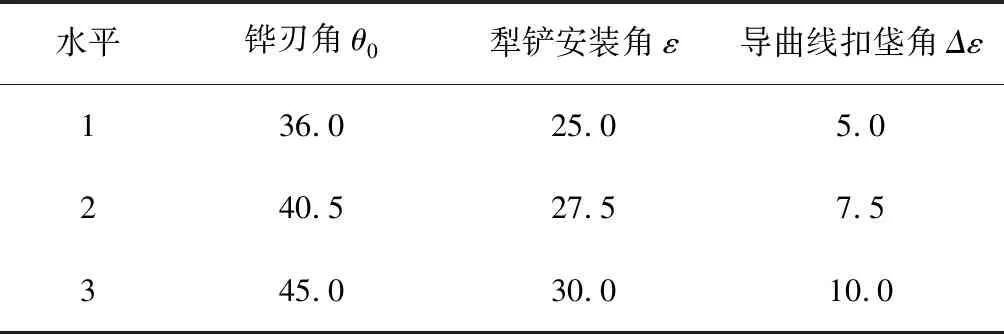
表2 试验因素水平

3.2 试验结果分析

3.2.1 犁体阻力动态变化规律

犁体耕作阻力随时间的变化曲线如图4所示。其中，AB时间段内，铧式犁铧尖开始进入土壤，随着时间变化，犁体所受阻力逐渐增加，耕作过程如图5(a)所示；之后，犁体全部进入耕作状态后，犁体所受阻力处于稳定阶段，如BC时间段所示，耕作过程如图5(b)所示。

图4 犁体阻力

θ0=36°、ε=25°、Δε=5°时的犁体阻力曲线如图4所示。

图5 犁体耕作过程

3.2.2 正交试验结果与分析

正交试验结果如表3所示。利用SAS软件对正交试验结果进行方差统计分析，结果如表4所示。

表3 正交试验方案与结果

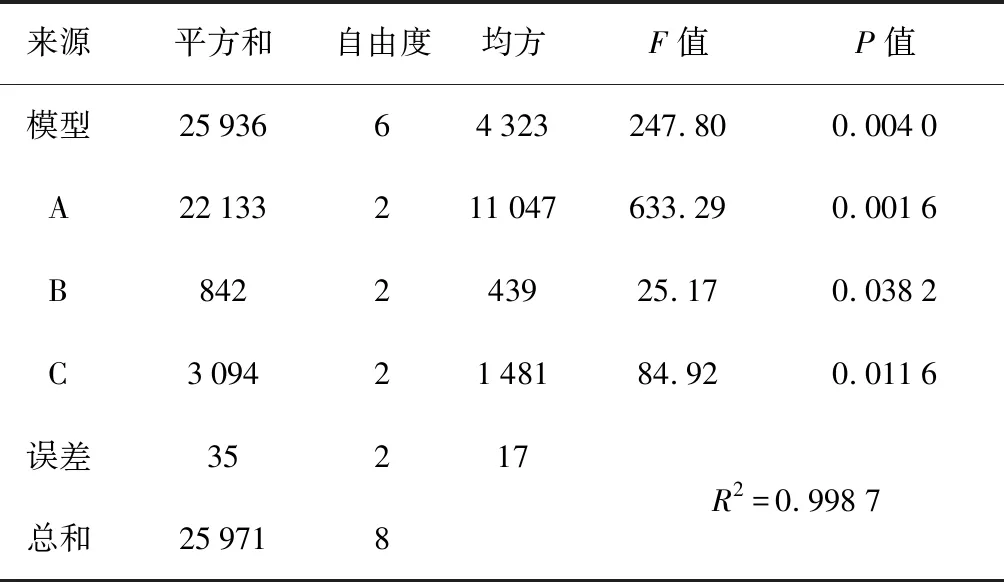
表4 正交试验方差分析

对试验结果进行极差分析，确定各因素主次影响顺序为A>C>B，其优组合为A3B1C1。模型的显著性P值为0.004 0，决定系数R2=0.998 7，方差分析结果可靠。方差分析可知：铧刃角对犁体阻力影响极显著(P<0.01),犁铲安装角、导曲线扣垡角对犁体阻力影响显著(P<0.05)。所以，在设计制造犁体曲面的过程中，应着重考虑铧刃角、犁铲安装角和导曲线扣垡角对犁体曲面的影响，以达到减小犁体阻力的目的。

选取最优水平组合A3B1C1进行试验，结果表明：当犁体完全进入耕作状态时，平均阻力为2 532N，比正交试验中9组试验结果的平均值减小了6.36%；铧刃角为45°时，犁体对土壤的推力方向在土壤颗粒与铧刃的摩擦锥外，且此时会产生剪应力最大断面，有利于犁体对土壤的滑切作用，从而减小犁体阻力；犁铲安装角越小，犁铧与沟底土壤的摩擦力越小，导曲线扣垡角越小，犁翼与土垡的摩擦作用越弱。理论分析与仿真优化结果一致，说明优化结果是有效可行的。

4 结论

1)采用水平直元线法设计了犁体曲面，运用SolidWorks软件对犁体曲面三维实体建模，且运用EDEM软件建立了犁体—土壤离散元模型。

2)仿真试验结果表明：犁体阻力随犁体与土壤接触面积的增大而增大，当犁体全部进入耕作状态时，犁体所受阻力达到2 621～2 795N，且趋于稳定。

3)正交试验表明：铧刃角对犁体阻力影响极显著(P<0.01)，犁铲安装角和导曲线扣垡角对犁体阻力影响显著(P<0.05)，且犁体结构最佳参数组合为铧刃角45°、犁铲安装角25°、导曲线扣垡角5°。该组合犁体阻力为2 532N，较9组试验结果的平均值减小了6.36%。研究结果为犁体曲面优化设计提供了一种离散元分析方法，并为犁体曲面的设计提供了参考。