遗传算法在农业移动机器人路径规划中的应用——基于矩阵二进制编码
薛文奎
(常州机电职业技术学院,江苏 常州 213164)
0 引言
农业移动机器人技术的最终目标是设计能够自主规划运动的自动机器人,因此来运动规划问题受到了该领域研究人员的广泛关注。一般而言,机器人运动规划问题是一个复杂而困难的问题。例如,真实环境中的机器人能够进行三维平移和旋转。通常,农业移动机器人的位置由与其自由度数量的多个参数来指定,运动规划的理论复杂度是机器人自由度数量的指数函数,这就是高自由度机器人难以解决的问题。为此在自然启发式遗传算法的基础上,结合矩阵二进制编码技术,探讨了一种解决自主机器人系统的路径规划与导航问题的方法。
1 矩阵二进制编码的遗传算法的实现
农业移动机器人在移动过程中没有绝对的最优路线,在对其进行路径规划过程中,一般是需要以最小代价计算出最优的路径。因此,本文采用基于矩阵二进制编码的遗传算法,用于搜索农业移动机器人路径导航和规划的最佳路径。本文提出的基于矩阵二进制编码的遗传算法,在导航和路径规划中能够对一系列的移动操作进行排序,从而使其在目标搜索中成功避障,通过该算法可以容易地实现农业移动机器人的实时决策、导航和路径优化。矩阵二进制编码的遗传算法的有效性取决于遗传染色体及其操作者。该算法通过对杂交、变异、竞争、选择和变量的分组分析,实现矩阵编码的变形及适应度的求取,从而使该遗传结构成为实现最佳适应性决策的基础。农业移动机器人采集其左边(LOD,Left Obstacle Distance)、前边(FOD,Front Obstacle Distance)和右边(ROD,Right Obstacle Distance)的障碍物距离作为数据输入(见图1),然后以航向角(HA,Heading Angle)的形式给出输出,从而实现避障的过程。该转换过程的核心主要包括生成编码、适应度函数、交叉和变异等4部分。
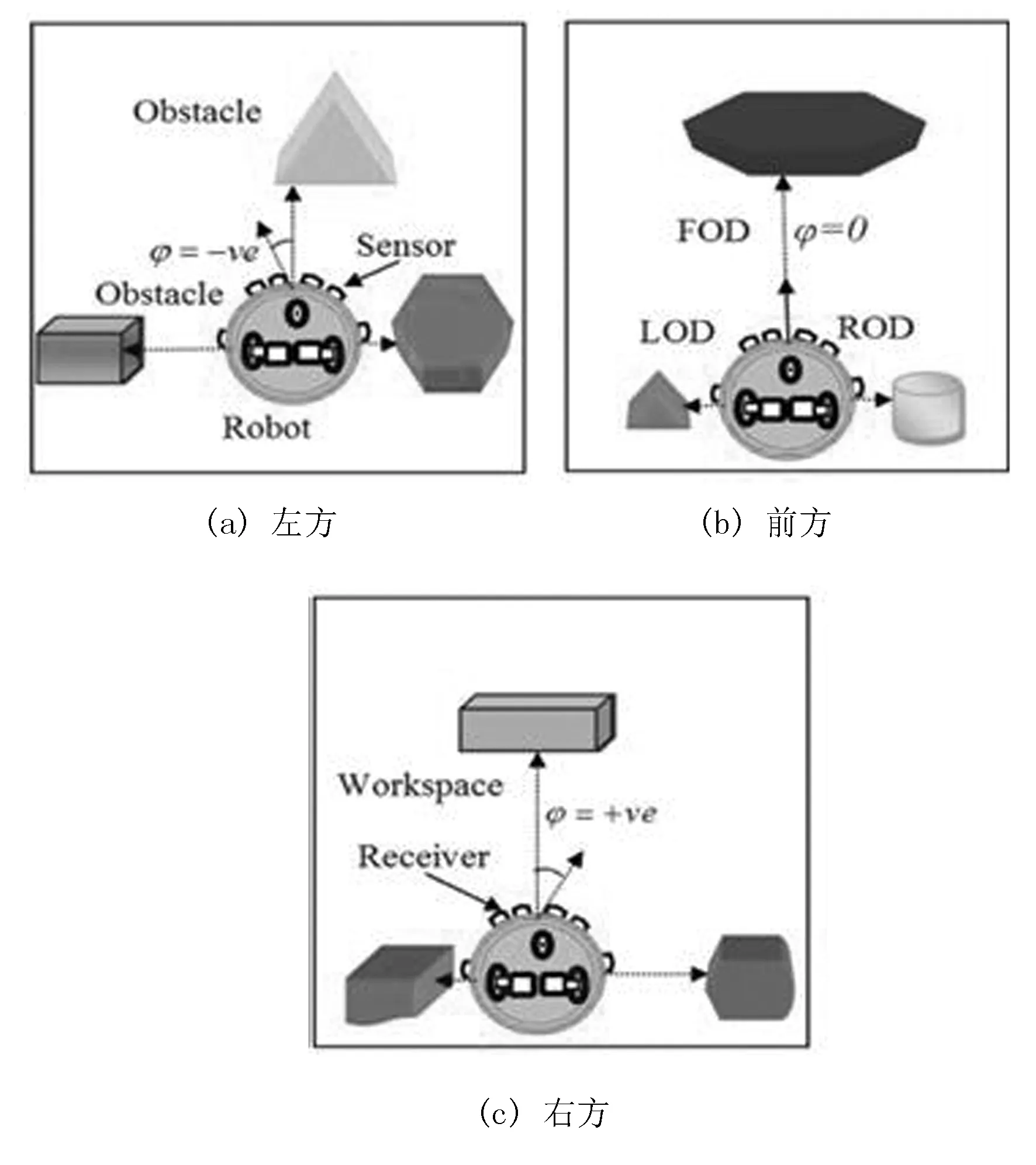
图1 障碍物位置示意图
1.1 矩阵二进制编码的生成
设置矩阵二进制编码的总集合P={P1,P2,…,Pn}。其中,Pi中染色体数目为5,元素结构为(i,j),则该二进制编码的矩阵为
(1)
其中,矩阵P的各列表示遗传算法结构的各个特征,具体为
(2)
其中,SC为转换符号。矩阵二进制编码的生成层的数学分析方法为:设定一个如下所示的新集合,即
S={FOD,LOD,ROD,HA,SC}
(3)
在公式(3)中,线性独立性是必需的,该集合避免了具有线性相关特性的元素。假设集合中的矢量都不能被表示为其他矢量的线性组合,则称该集合是线性无关的,因此FOD、LOD、ROD、HA和SC组成的集合S被称为线性无关。
Pi,jFOD+Pi,jLOD+Pi,jROD+
Pi,jHA+Pi,jSC=0
(4)
假如一组矢量不是线性独立的,那么它们被称为线性相关。
1.2 矩阵二进制编码的适应度函数
适应度函数是遗传算法进化的关键,适应度函数的生成和合理性对于实现导航和路径规划的最佳决策至关重要。农业移动机器人的避障机制和最优路径生成的效率取决于适应度函数的精度。该控制算法遵循最佳功能为
fTotal=(c1,c2,c3,c4,c5)Tr(p)
(5)
其中,Tr(p)为迹线,即p的对角元素之和。
Tr(p)的表达式为
(6)
(7)
假设目标角度是TA,航向角度是HA,那么最适合的群体为(cFOD-pci,1)、(cLOD-pci,2)和(cROD-pci,3)。
矩阵二进制编码的适应度函数数学分析方法为:基于FOD、LOD和ROD的线性无关集合主要由以下相应的向量建立,即
S={cFOD,cLOD,cROD}
(8)
若集合中的矢量都不能被表示为其他矢量的线性组合,则称该集合S是线性无关的;反之,则称为线性无关。
Pci,jcFOD+Pi,jLOD+Pi,jROD=0
(9)
如果一组矢量不是线性独立的,那么它们被称为线性相关。
1.3 矩阵二进制编码的交叉
矩阵二进制编码的交叉主要是对概率分布进行研究,在该过程中,最初从选择的群体中选择染色体,按某种方式单点交叉两个父亲染色体,产生两条后代染色体。基于矩阵二进制编码的遗传算法在农业移动机器人路径规划中,主要是对到达新位置航向角的决策变量进行判断。二值向量{0,1}及语言变量为FOD、ROD及LOD编码的交叉为
进行矩阵二进制编码的交叉层的数学分析,交叉表达式为
如果一组矢量不是线性独立的,那么它们被称为线性相关。
1.4 矩阵二进制编码的变异
基因组合负责着每一个遗传操作,染色体的变化率常由变异算子测量和引用,变异算子为农业移动机器人避障行为提供参考。一般而言,一对一对应的序列校正被称为突变操作,突变的过程被描述为一个随机数。具体解释如下:
假设变异向量集为λ={λ1,λ2,...,λn},染色体集合为c={c1,c2,...,cn}。令f(λ)为一个变异算子,其映射从λ到c,如图2所示。

图2 变异向量和染色体向量映射示意图
chromosome vector mapping
在分析时,域为λ,共域为c,f的范围为f(λ)。从遗传基因的观点来看,该假设是根据基因的自然行为来执行操作。对于该突变过程,染色体的位置可以由以下矩阵表示,即
(10)
(11)
因此,变异算子向量为
D={D1,D2,…Dn}
(12)
进行矩阵二进制编码的变异层的数学分析,采用式(12)中的元素向量来定义新集合为
S={D1,D2,…Dn}
(13)
若集合中的矢量都不能被表示为其他矢量的线性组合,则称该集合S是线性无关的;反之,则称为线性无关。
λiD1+λiD2+…λiDn=0
(14)
如果一组矢量不是线性独立的,那么它们被称为线性相关。
根据基于矩阵二进制编码的遗传算法,任何农业移动机器人的工作环境都可以从混沌转变为一个个阵列,然后实现导航和路径规划。
2 农业移动机器人路径规划问题分析
本章将详细阐述农业移动机器人运动路径规划问题。假设农业移动机器人的运动环境为E,也就是将障碍物和机器人运动环境视为E,E中的所有障碍物集合为O,其定义为
O={o1,o2,…,om}
(15)
其中,oi为农业移动机器人运动环境中的第i个障碍物。另外,农业移动机器人禁止移动的空间被定义为
(16)
其中,Sforb为E中所有障碍物的结合体。
农业移动机器人能够自由移动的空间用S自由表示,其定义为
Sfree=ESforb
(17)
农业移动机器人运动环境和Sfree集合如图3所示。其中,白色区域为Sfree,灰色区域为Sforb。

图3 农业移动机器人障碍物和自由区域示意图
agricultural mobile robots
前面介绍农业移动机器人运动规划问题的符号含义,具体定义为
(18)
其中,T(pstart,ptarget)为开始(pstart)和目标点(ptarget)之间的最佳路径;集合Γ为Sfree集合中pstart与ptarget之间的所有可行路径。此外,d(p)表示路径P的长度,其计算公式为
(19)
其中,‖pi-pi-1‖为点pi和pi-1之间的欧氏距离。
(20)
其中,(xi,yi)为pi的坐标。
通过上述要点,能够将机器人运动规划优化问题转换成建模问题。
3 农业移动机器人路径规划仿真分析
前文介绍了矩阵二进制的遗传算法在农业移动机器人路径规划中的潜力。本章在具有I7处理器(3GHz)、8GB RAM、500GB硬盘、Windows7(64位)OS和NVIDIA(1GB)图形卡的PC上进行了MatLab仿真分析。在模拟过程中,农业移动机器人不知道环境中障碍物的位置。最初,农业移动机器人仅提供了有关其起始位置和目标位置的信息。在模拟过程中,农业移动机器人显示为一个小圆圈,并装载有传感器模块来计算FOD、LOD、ROD和HA。农业移动机器人作业环境如图4所示。其中,黑色部分为障碍物。试验中,二维空间的作业区域的起点位置为start,终点位置为target。

图4 农业移动机器人作业环境示意图
机器人开始移动直到达到目标,且在环境无障碍时无需激活矩阵二进制编码的遗传算法;但当障碍物进入机器人的路径时,它会激活二进制编码的遗传算法以避免障碍物。农业移动机器人在静态环境中各种初始位置和目标位置的路径规划,通过反复迭代学习,不断逼近,求出了两种不同模型区域的最优运动轨迹。仿真求最优轨迹的实验结果如图5所示。农业移动机器人通过激活矩阵二进制编码的遗传算法作为智能机制来观察路径中存在的障碍物并产生无障碍轨迹。
仿真结果显示了农业移动机器人在存在复杂障碍物的情况下的路径规划与导航。当农业移动机器人观察其路径上的移动障碍物时,会调整速度,有时会停下来做出决定。采用矩阵二进制编码的遗传算法进行路径规划中,其迭代次数如图6所示。

图5 Matlab仿真实验结果

图6 农业移动机器人路径规划迭代次数
图6显示了本文采用的矩阵二进制编码的遗传算法对图4中移动环境迭代次数的行为。其中,x为迭代次数,y轴为100次实验中的平均值和最佳适应值。
由图6可以看出:针对两种障碍物与路径不同的模型区域,农业移动机器人成功地求解出从开始到结尾并成功躲避障碍物的最优轨迹规划。根据多次实验对比,所求路径是该条件下机器人穿过障碍物耗时最少、运动代价最小的路线。
4 结论
基于矩阵二进制编码的遗传算法,通过采集左边、前边和右边的障碍物距离作为数据输入,输出追踪最佳路径长度和导航时间,形成最优矩阵决策,实现农业移动机器人和目标之间的映射关系。仿真实验结果表明:农业移动机器人在存在复杂障碍物的情况下能够实现路径规划与导航,且所求路径是该条件下机器人穿过障碍物耗时最少、运动代价最小的路线。

