甘蔗收获机切刀负载压力影响因素试验研究
麻芳兰,丁 翔,任晓智,郭衍超,赵 静
(广西大学 机械工程学院,南宁 530004)
0 引言
甘蔗在我国南方热带地区广泛种植,成为该地区的主要经济作物之一。作为中国最大的蔗糖生产基地,广西产糖量基本稳定在全国总产量的60%左右,甘蔗已成为该地区主要经济收入来源[1]。由于蔗地地势起伏变化较大,切割器切割甘蔗时出现过切或漏切现象,导致甘蔗收割时出现收割损失大的情况[2]。由于国外联合甘蔗收获机体型大,不适合我国南方地势起伏大、面积小的丘陵地区,因此研发制造出成熟的适于我国国情的甘蔗收获机具有重要意义。
根据课题组前期研究,王增等[3]在对甘蔗收割机入土切割甘蔗进行试验研究及理论分析的基础上,拟合出切割入土深度与负载压力的关系曲线,从而为甘蔗入土切割试验研究提供数据支持。杨望等[4]采用ANSYS/LS-DYNA软件利用反求技术建立了土壤-甘蔗-切割器系统的动力学模型,进行单因素仿真试验,建立相关数学模型。Candelabrum等[5]运用响应曲面设计中的Doehlert设计方法建立了液-液系统中三因素和提炼铀含量的函数关系模型,得出最优的参数组合。Yesim Qguz等[6]利用Doehlert设计方法优化发光纺织结构,拟合实验数据,建立较优的数学模型,求出最优解。赵静和蔡力等[7-8]通过研究土壤特性对切刀负载压力的影响,综合采用正交试验和神经网络预测,分析出各因素影响刀盘负载压力的规律,找出了各个影响因子的主次顺序,为最终实现通过切割系统负载压力控制切刀入土深度的目标提供了数据支撑。
本文通过课题组自主研制的甘蔗收割机实验平台,通过ANSYS软件仿真分析和试验研究的方法来探讨刀盘倾角、刀盘转速、入土深度、甘蔗密度和进给速度对甘蔗收割机出现收割损失大的影响,最终建立切刀负载压力与入土切割深度关系的数学模型,从而利用这些关系使得甘蔗收割机在切割过程中能够自动控制入土切割始终处在负载压力较小的深度。
1 甘蔗入土切割负载压力影响因素分析
通过实地调研及理论分析得出:影响甘蔗收割机负载压力的因素为刀盘倾角、刀盘转速、入土深度、甘蔗密度和进给速度。由于前课题组[9]已对刀盘转速、入土深度、甘蔗密度和进给速度进行了物理单因素试验分析,因此本文将不再赘述。
根据库伦定律,土壤对切削土壤器械工作表面的摩擦阻力,是土壤对切削土壤器械工作表面法向压力的函数[10],公式表示为
F=fcNcosθ+A
(1)
式中F—摩擦阻力;
fc—滑动摩擦因数,fc值取决于相对运动速度、接触物体的材料及表面光滑程度等;
N—法向压力;
θ—刀盘倾角;
A—接触表面间的附着力。
随着刀盘倾角的减小,刀盘受到法向压力N增大,刀盘和土壤接触面积增大使接触表面间的附着力A增大,不仅土壤对切割器的摩擦力增加,且会引起刀盘自动提升需要更大的提升力。
2 入土切割单因素仿真试验研究
2.1 切割器-甘蔗-土壤几何模型的建立
为了与甘蔗地实际切割甘蔗条件相符,本文采用的切割器仿真模型与第2台物理样机的切割器尺寸一致;同时,为了缩短仿真周期,本文做了相应的简化。建立的甘蔗-土壤-切割器如图1所示。

图1 甘蔗-土壤-切割器仿真模型Fig.1 Simulation model of sugarcane-soil-cutter
2.2 切割器-甘蔗-土壤仿真模型的建立
2.2.1 单元类型与材料选择
刀盘、甘蔗与土壤模型的单元类型选择3D SOLID164单元类型,土壤材料模型使用MAT147材料模型,模型采用Mohr-Coulomb屈服准则[11-13]。根据前课题组[14]的仿真试验研究,甘蔗模型材料选用Orthotropic(线弹性正交各向异性材料模型)材料,甘蔗密度1.09g/cm3。材料参数如表1所示。
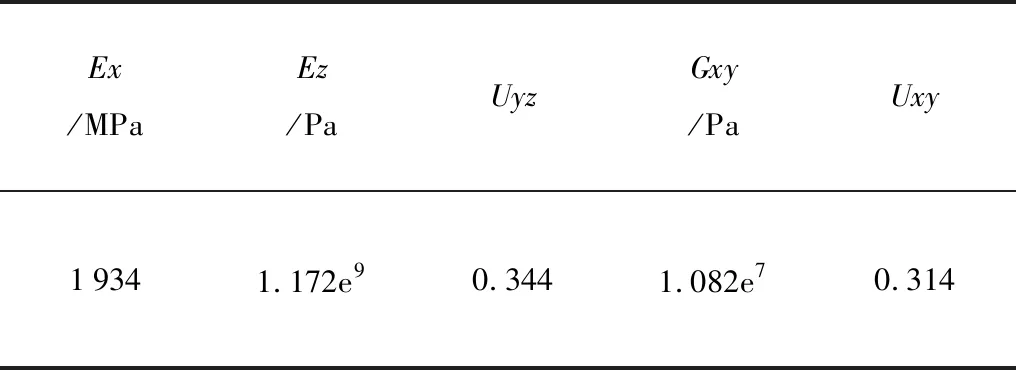
表1 甘蔗材料参数Table 1 Parameters of sugarcane material
2.2.2 刀盘倾角仿真与分析
仿真条件:入土深度由0逐渐切深至60mm,甘蔗株数为1株,切割器进给速度为0.4m/s,土壤硬度设置为6.4kg/cm2,土壤含水率24.1%,刀盘转速设置为700r/min。仿真试验方案如表2所示。
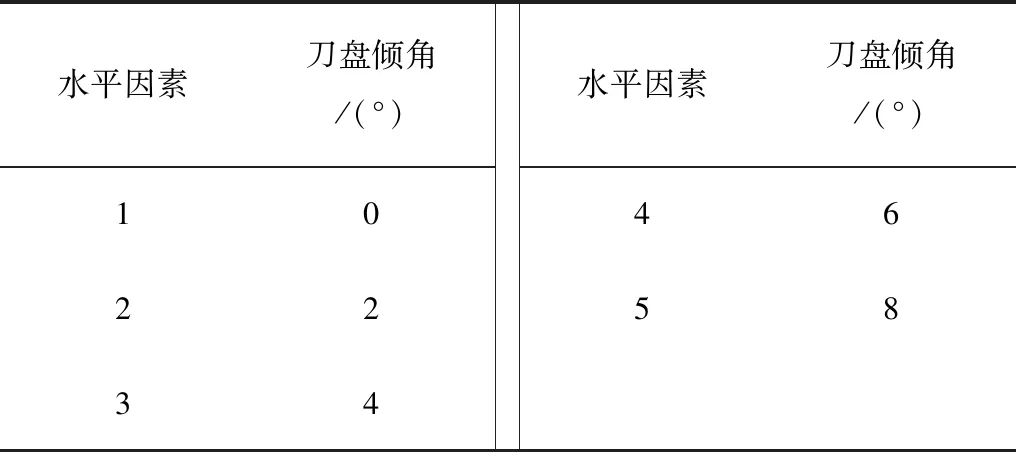
表2 仿真试验方案Table 2 Simulation test scheme
2.2.3 不同刀盘倾角的甘蔗切割受力分析
刀盘倾角为0°时,得到的切割器入土切割甘蔗的最大切割力3.896 8kN;刀盘倾角为2°时,得到的切割器入土切割甘蔗的最大切割力2.923 1kN; 刀盘倾角为4°时,得到的切割器入土切割甘蔗的最大切割力2.320 3kN;刀盘倾角为6°时,得到的切割器入土切割甘蔗的最大切割力2.562 9kN;刀盘倾角为8°时,得到的切割器入土切割甘蔗的最大切割力2.715 3kN,不同倾角对切割力受力的影响如图2~图6所示。
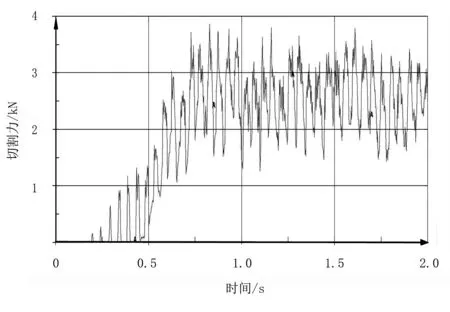
图2 刀盘倾角为0°切割器受力变化情况Fig.2 The force of the cutter angle of the 0 degree cutter
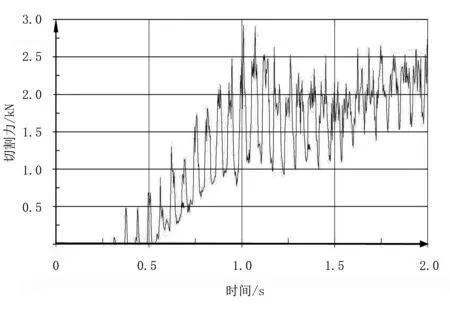
图3 刀盘倾角为2°切割器受力变化情况Fig.3 The force of the cutter angle of the 2 degree cutter
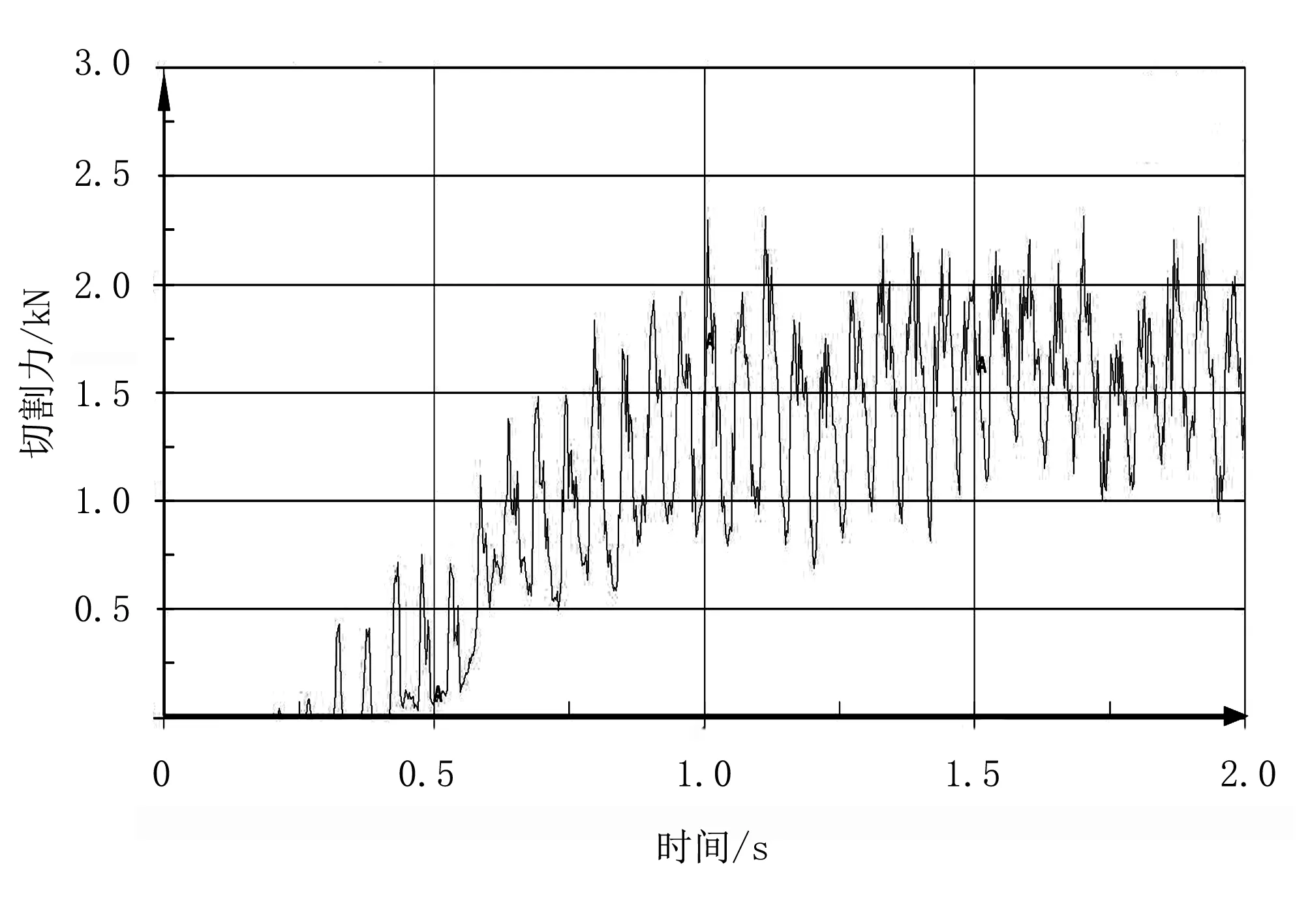
图4 刀盘倾角为4°切割器受力变化情况Fig.4 The force of the cutter angle of the 4 degree cutter
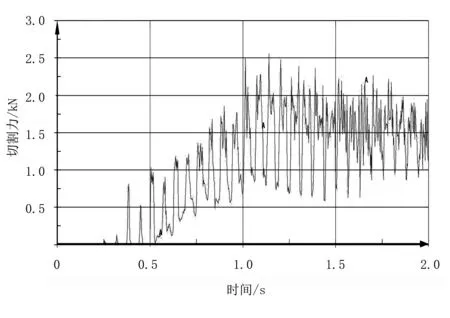
图5 刀盘倾角为6°切割器受力变化情况Fig.5 The force of the cutter angle of the 6 degree cutter
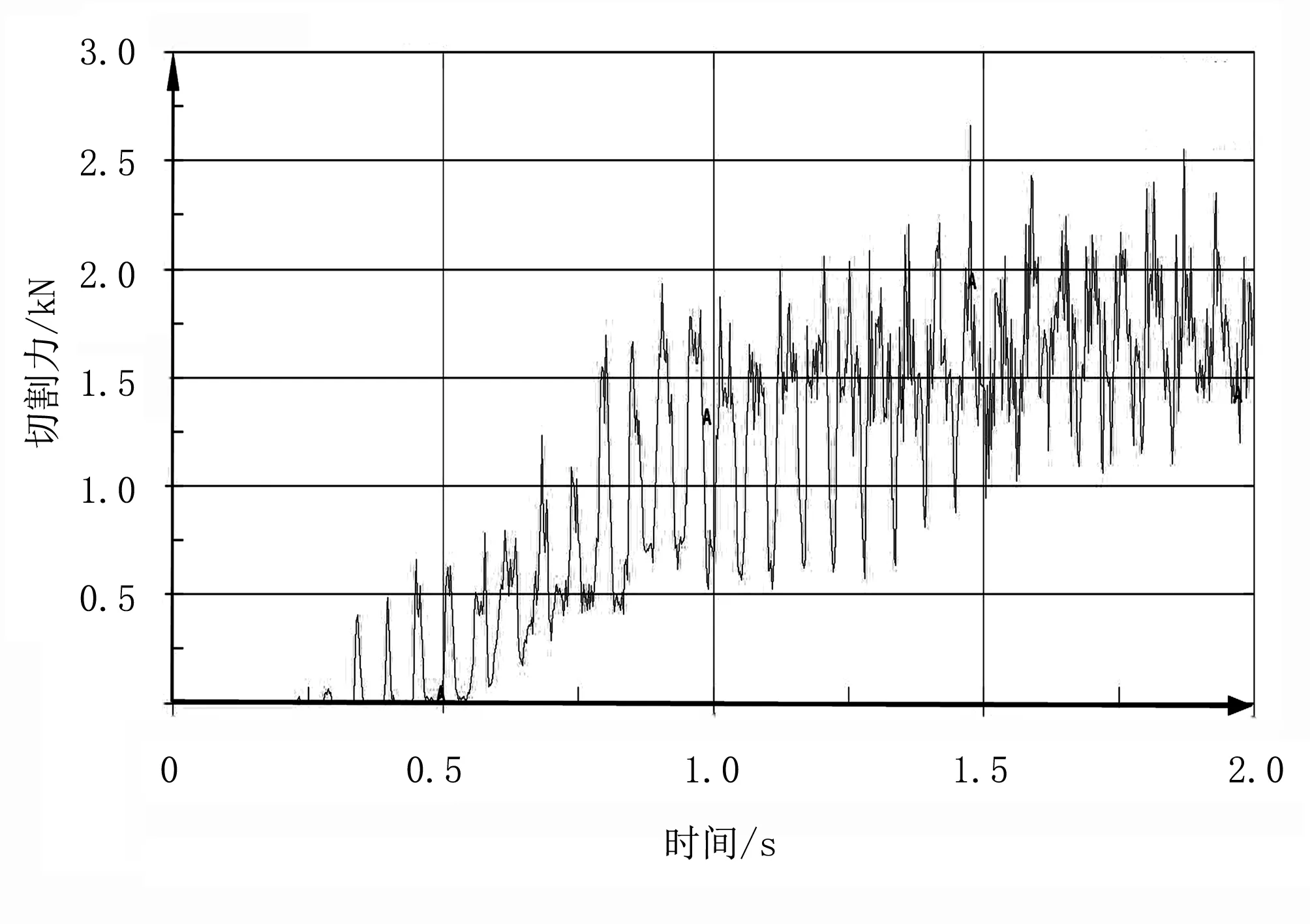
图6 刀盘倾角为8°切割器受力变化情况Fig.6 The force of the cutter angle of the 8 degree cutter
综合以上在不同刀盘倾角下的切割力值,可以看出:随着刀盘倾角的增大,切割器入土切割甘蔗的切割力先减小后增加;刀盘倾角较小时,切割力达到稳定状态所需的时间短,切割器入土切割受到冲击力大,需要切割器及刀架的刚性好,因此研究不同的刀盘倾角对负载压力的影响是有必要的。由曲线可知:在甘蔗入土切割仿真试验中,切割曲线具有波动,这是因为切割器入土切割时会产生振动,土壤生成的SPH粒子也会脱落,导致土壤对切割器的阻力有一定的变化规律[15]。
3 入土切割试验研究
3.1 试验仪器
本试验在课题组自主研制的液压驱动甘蔗切割实验平台上进行。切割系统实验平台主要由切割支架、液压马达、砍蔗刀盘、提升液压缸、土壤模型、数字变频器 、行位继电器 、减速器及电机等组成。甘蔗夹持器和土槽装置采用本课题组赵静[6]设计的试验设备,该设备根据甘蔗种植农艺参数设计,模拟甘蔗田间生长状况,一次可以切割两簇甘蔗,试验指标主要是采集驱动刀盘转动的液压马达进口处的负载压力。需要的试验设备有:CT涡轮流量传感器、压力传感器、LERO智能测试仪和笔记本电脑。
3.2 试验方案
在课题组自主研制的实验平台上进行切割甘蔗试验,研究各因素对试验指标的影响效果。DM设计的区域位于球形上,其试验点均匀分布在球形上。矩阵的排列由试验的因素和水平数目及其设计矩阵编码值确定[16]。
总的试验次数N可由公式N=k2+k+C0算出。其中,k为因素的数目;C0为中心点的数目(试验次数)。本试验选取刀盘倾角x1、入土深度x2、刀盘转速x3、进给速度x4、甘蔗密度x5, 每个因素按照Doehlert matrix设计矩阵选取,得到的试验方案与试验结果如表3所示。
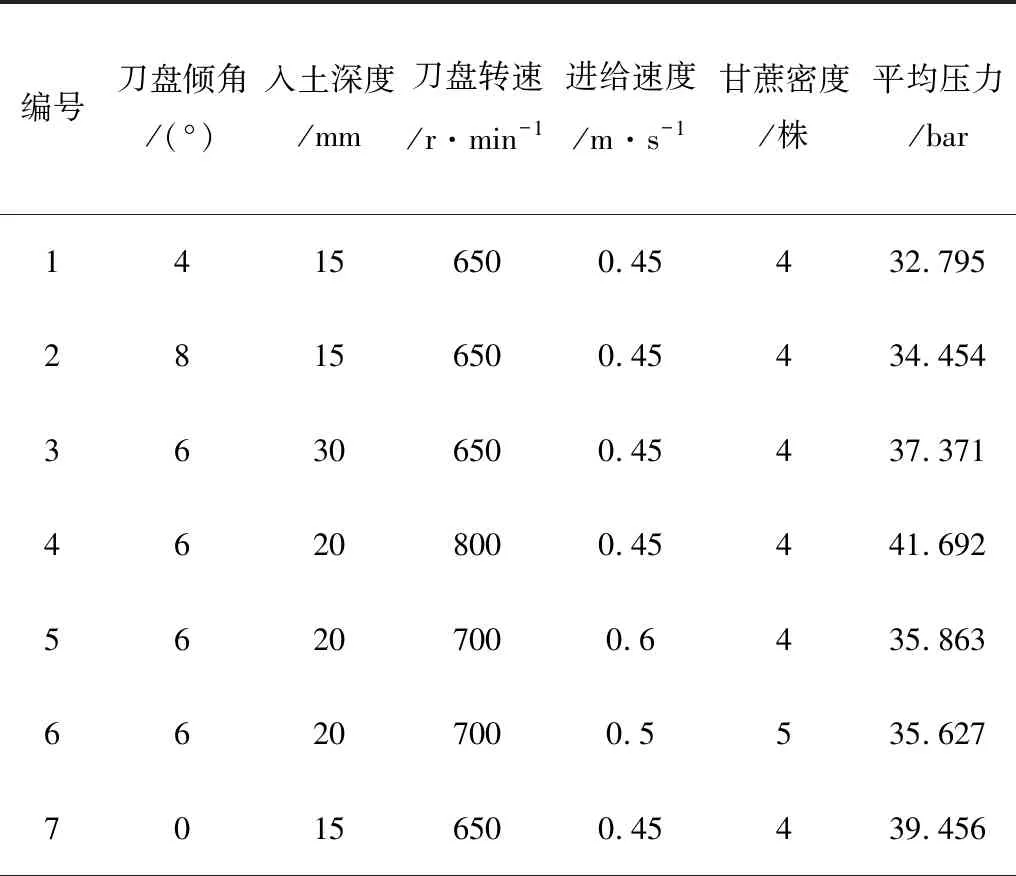
表3 Doehlert matrix设计试验结果Table 3 Doehlert matrix design test results
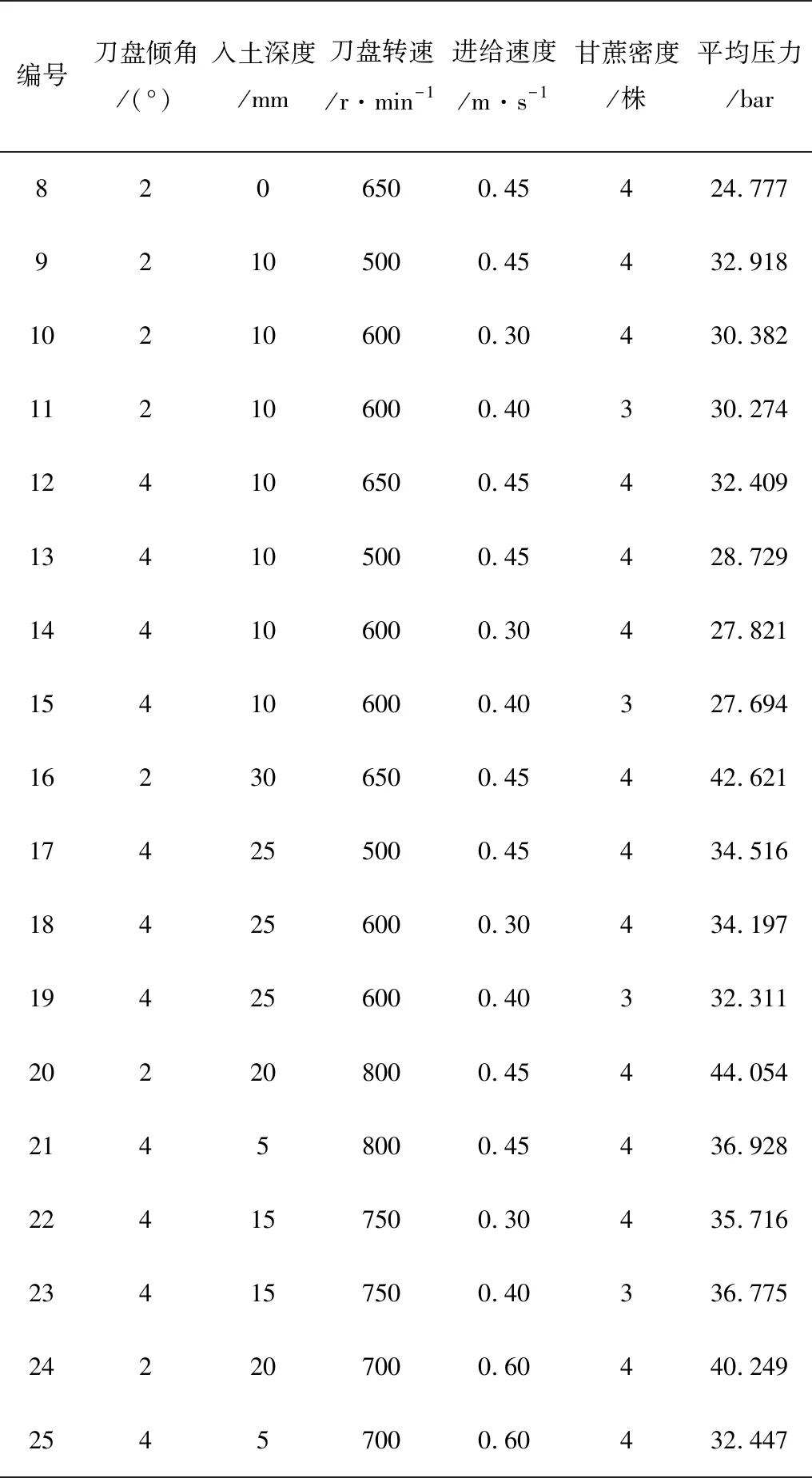
续表3
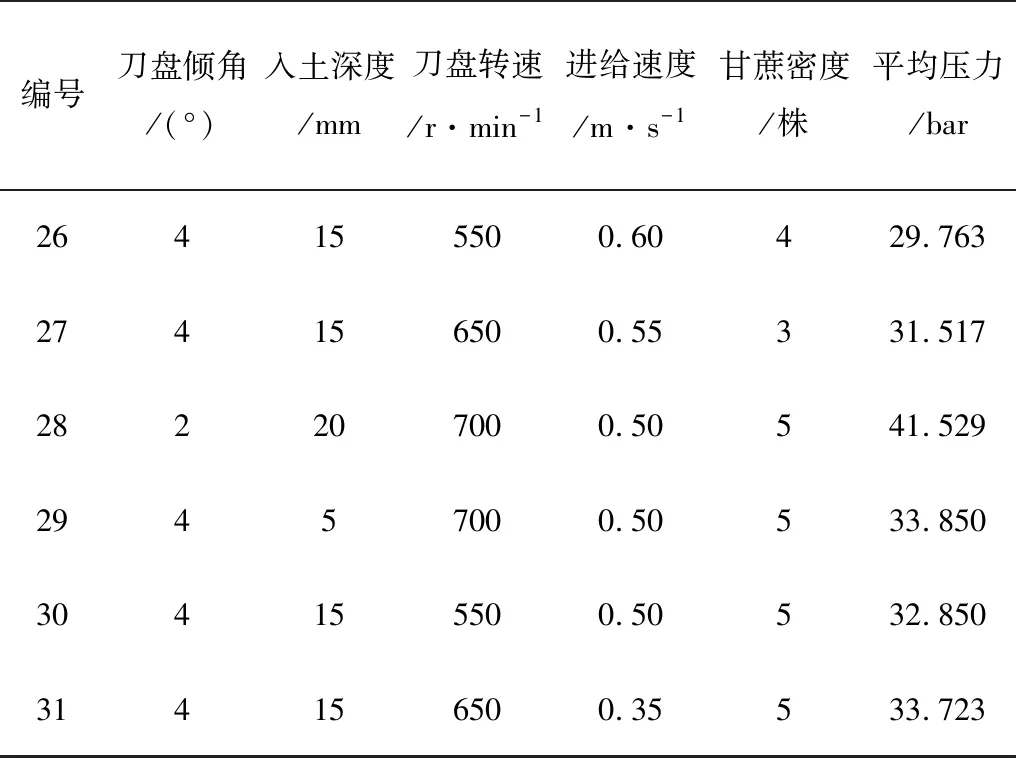
续表3
3.3 试验数据回归分析
本试验研究的因素较多,试验数据结果分析时,只考虑两两因素的交互作用。设其二次回归方程一般形式为
其中,p为变量个数;j=0,1,2,3,…,p;i=0,1,2,3,…,p-1。
向后剔除法是让所有的自变量回归方程逐个删除。在删除过程中,与因变量之间最小的偏相关系数的自变量将会首先考虑被删除,过程直到回归方程中再也没有符合删除条件的自变量时终止[17]。
经过计算机计算后得出12个回归模型,根据模型的假设检验水平值相比较,最终选择第12个的回归模型最优,模型参数如表4所示。
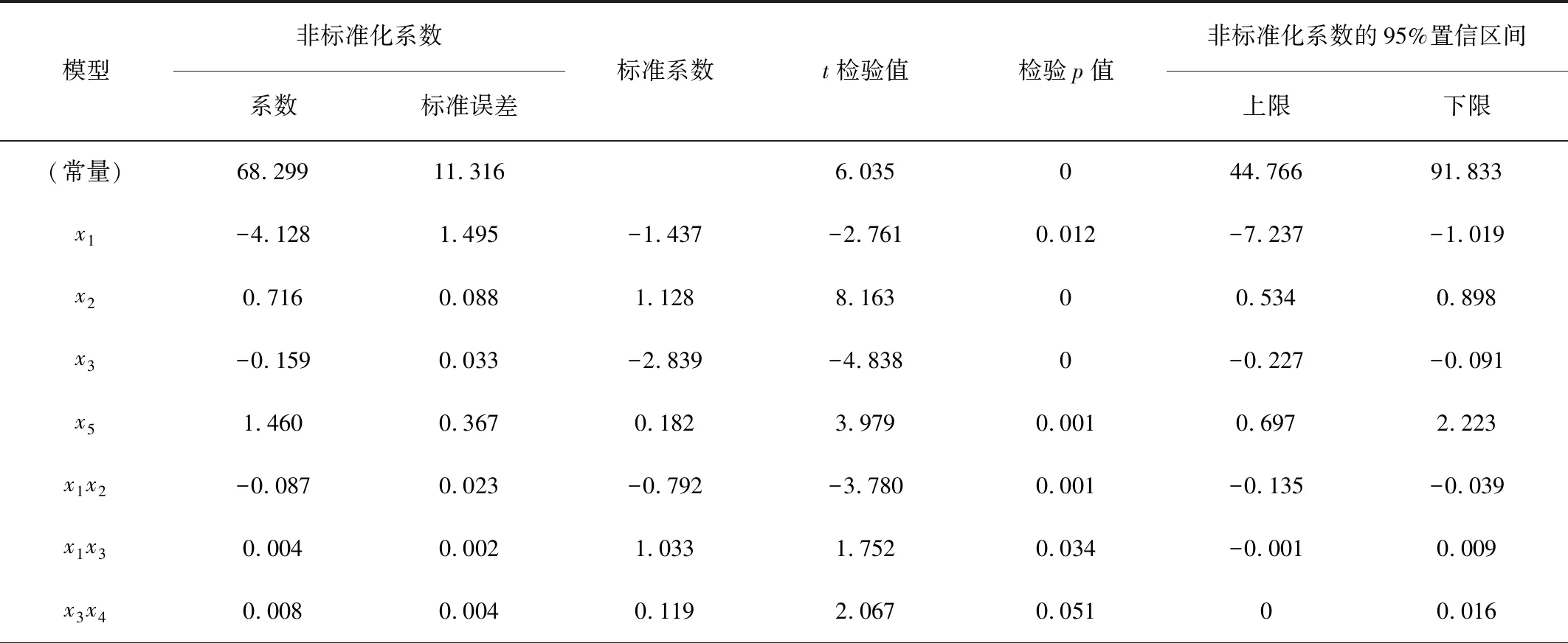
表4 模型参数Table 4 Model parameters

续表4
x1为刀盘倾角,x2为入土深度,x3为刀盘转速,x4为进给速度,x5为甘蔗密度。
由表4得出回归方程为
y=768.299-4.128x1+0.716x2-0.159x3+
1.460x5-0.087x1x2+0.004x1x3+0.008x3x4+
3.4 检验回归及其系数的显著性
试验数据应用统计分析,检验回归方程和回归系数显著性,结果如表5和表6所示。
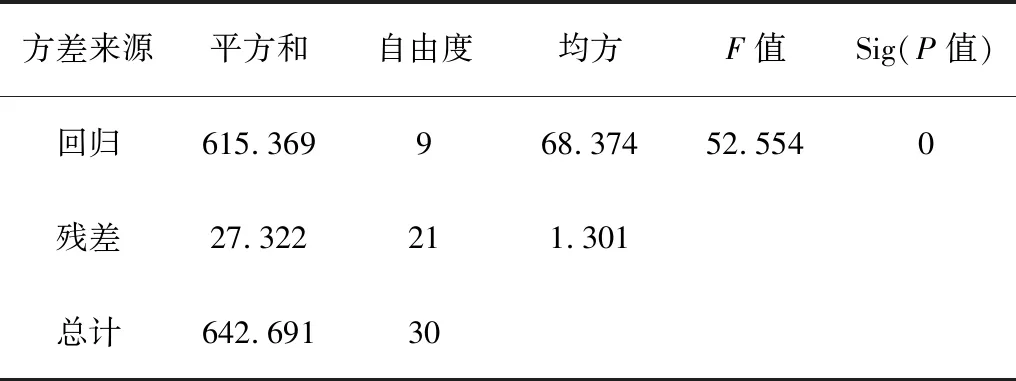
表5 方差分析表Table 5 Variance analysisTable
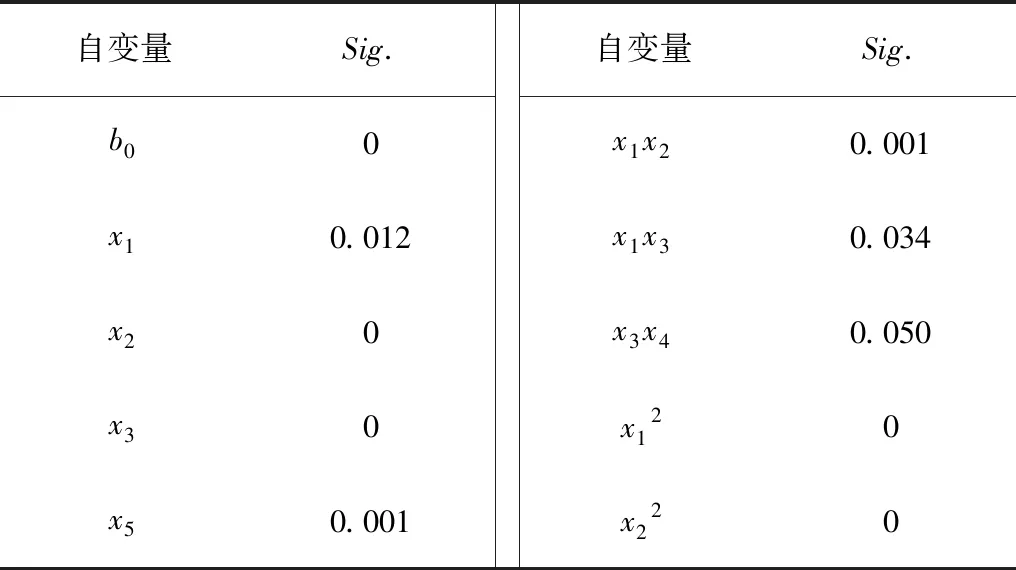
表6 回归系数显著性Table 6 Regression coefficient saliency
由表5可知:回归方程的sig=0水平上高度显著。由表6可知:回归方程的各个系数都小于等于0.05,表明回归方程具有较高的精确度。
4 结论
1)查阅相关资料理论分析出甘蔗收割机切割系统负载压力的主要影响因素,对影响因子的水平进行实地调研,找出其影响因子的取值范围。
2)利用课题组前期实地调研收集到的蔗地土壤参数及甘蔗力学特性参数数据,在ANSYS/LS-DYNA软件中,建立切割器-甘蔗-土壤模型的动力学模型,对不同的刀盘倾角进行仿真试验,并将仿真试验结果与理论分析结果相互验证,检验仿真试验的正确性。
3)通过Doehlert matrix设计进行物理试验,建立切割负载压力与影响因素之间的数学模型,为甘蔗收割机的刀盘入土切割深度自动控制信号的获取提供数据支撑。

