基于SVM的RBF网络在农机总动力预测中的应用
吴志辉,王福林,董志贵
(东北农业大学 工程学院,哈尔滨 150030)
0 引言
农机总动力水平是农业机械化水平的重要指标,也是政府部门指定农业机械化发展规划的重要依据,因此对农机总动力的预测具有重要意义。目前,关于农机总动力的预测有多种方法:人工神经网络的效果较好,但大多数研究都是与BP神经网络有关的[1-3];径向基函数(Radial Basis Function,RBF)神经网络[4]结构简单、学习速度快。其核心思想就是在低维空间非线性相关关系通过基函数映射到高维空间后可能成为线性相关的,这样就可以用线性方法解决原问题。在RBF神经网络中,确定基函数中心的数量、位置以及宽度是RBF神经网络的关键[5]。因此,人们一直试图将各种高效的聚类算法应用在计算RBF神经网络的基函数中心的过程中,最常用的一种做法是采用k-means聚类法来确定基函数中心,但需要预先设定希望得到的聚类数,这在复杂的实际情况中是很难做到的。针对K-means聚类的不足[6],潘琪等人提出利用系统聚类的方法来确定基函数的中心的方法,但系统聚类和K-means在本质上都是贪心算法的一种,也就具有了贪心算法的缺点,算法在每一步所做的决策对当前状态来说都是最优的,这样得到的最终解很可能不是全局最优解,且系统聚类法受异常值的影响较大[7],算法结构不稳定。为此,提出了一种支持向量机聚类来确定基函数中心的方法,具有很强的普适性和鲁棒性,弥补了K-means和系统聚类在确定RBF神经网络基函数中心过程中的不足,且把改进的RBF神经网络应用到黑龙江省农机总动力的预测中,得到了很好的效果。
1 RBF神经网络基本原理
RBF神经的结构如图1所示。
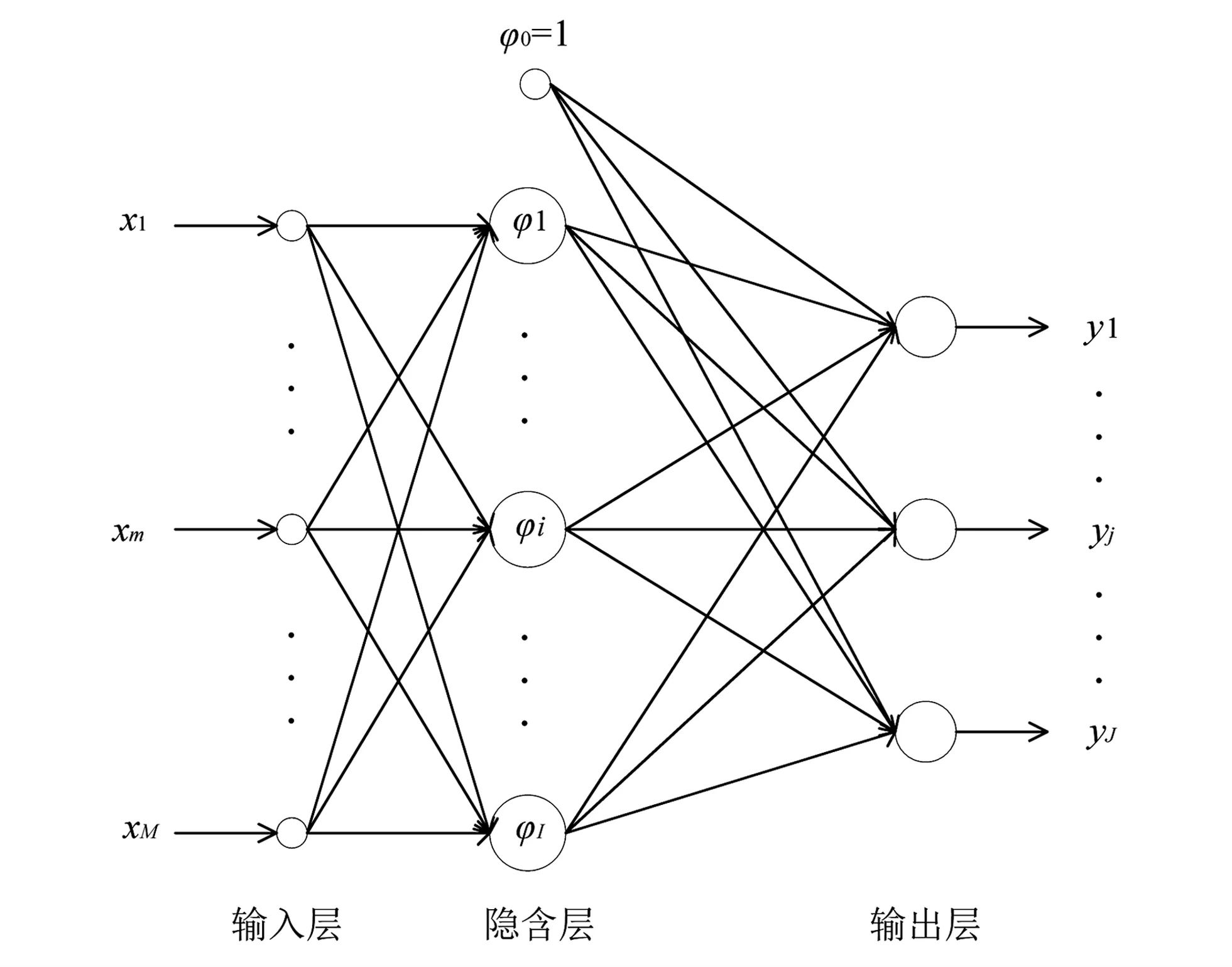
图1 RBF神经网络结构图Fig.1 RBF neural network structure
第1层为输入层,用来接收外界信号;中间层为隐含层,将输入信号进行非线性转换;第3层为输出层,将对输入信号的响应传递出去。
该网络输入层的神经元个数为n,隐含层神经元的个数为h,输出神经元的个数为m。设RBF网络的第i个输入向量为Xi=[x1,x2,…,xn],基函数中心为[C1,C2,…,Cj,…,Ch]T,且有Cj=[c1,c2,…,cn],即每一个基函数中心的维度要与输入向量的维度相同,b=[b1,b2,…,bm]T为阈值。隐含层与输出层之间的非线性映射为φ(‖Xi-Cj‖),则第i个输入的输出为
(1)
令w0=-1,φ0=b,则有
(2)
设输入向量的个数为P,则有
(3)
令φij=φ(‖Xi-Cj‖),i=1,2,…,p;j=1,2,…,m,那么可将上述方程组改写为
(4)
进一步可以表示成
ΦW=D
(5)
其中,Φ为映射矩阵;W为系数矩阵;D为输出矩阵。
RBF思想的核心是核方法的思想:低维空间的非线性相关关系经过核函数映射到高维数据空间很可能成为线性相关的。在映射过程中,离基函数中心的距离越近的位置对响应的影响越大。在RBF神经网络中,基函的宽度就是基函数的探测区间,基函数的数量就是隐层节点的数量。RBF神经网络的构造过程就是确定基函数中心及连接权值的过程,确定基函数中心需要考虑中心的数量、位置及宽度等几方面。
2 基于SVM的RBF神经网络学习算法
一般来讲,RBF神经网络的构建有两个阶段:首先,利用某种聚类方法把样本集合划分为h类,将每个类的中心作为RBF基函数的中心;其次,根据聚类结果确定和基函数中心相关的参数,并确定隐含层与输出层之间的权值。从RBF的原理可以看出:基函数的中心及其相关的参数是设计RBF网络的关键。针对传统聚类方法的不足,本文提出利用支持向量机(SVM)来确定基函数的中心。
SVM与其他机器学习方法不同,过去的机器学习方法大多都是基于经验风险最小化原则(ERM),而SVM是一种基于结构风险最小化(SRM)原则的学习算法;而基于SVM的聚类方法继承了SVM算法的所有优点。
本文中,使用高斯核函数将数据点从数据空间映射到高维特征空间。在特征空间中,寻找包围同类所有样本的最小球体,这个球体被映射回原数据空间,在那里它形成一个围绕数据点的轮廓,这些轮廓称为聚类边界,每个单独轮廓所包含的点就属于同一类别。随着高斯核的宽度减小,数据空间中断开的轮廓的数量增加,此时分类的数量就越多。同时,该方法还可以通过采用松弛变量(SVM中的软间隔常数)来处理异常值[8]。
接下来,详细介绍支持向量机聚类算法:
设{xi}⊆X是N个实例点的数据集,X⊆Rd为原数据空间。使用从X到某些高维特征空间的非线性变换φ,寻找半径为R的最小包围球体。由以下约束条件来描述,即
‖Φ(xj)-a‖2 (6) 其中,‖·‖为欧几里得范数;a是球体的球心。通过加入松弛变量ξj来结合SVM中的软间隔,则 ‖Φ(xj)-a‖2 (7) 其中,ξj≥0。为了解决这个问题,引入拉格朗日乘数,即 (8) 其中,βj≥0和μj≥0是拉格朗日乘子;C是一个惩罚因子,可以平衡球半径和松弛因子比重,通常取[0-1];Cξj是一个惩罚项。 将L分别对R、a和ξj求导得 (9) (10) (11) 由KKT互补条件可得 ξjμj=0 (12) (13) 下面根据方程式(13)进行如下讨论: 1)ξi>0且βi>0,由式(12)得此时μi=0,点xi位于特征空间球体的外部;又因为βj=C,所以该点对构造超球体有影响,此时,这个点被称为受限支持向量(BSV)。 2)ξi>0且βi>0,此时μi>0,且‖Φ(xj)-a‖2=R2成立,所以对应的xi位于高维特征空间的超球体表面,又因0<βi 3)若βi=0,对应的xi位于高维特征空间的超球体内部,这样的样本点称为内点,它们对于构造超球体或者支持函数并不起任何作用。 利用以上这些关系,可以消除变量R、a和μj,将拉格朗日变成对偶形式,它是变量βj的函数,即 (14) 由于变量μj不出现在拉格朗日函数中,可以用以下约束代替,即 0≤βj≤C,(j=1,…,N) (15) 加入核函数后的拉格朗日W,写成 (16) 本文的核函数选择高斯核函数,则 K(xi,xj)=e-q‖xi-xj‖2 (17) 其中,q为宽度参数。 义特征空间中样本点x距球体中心的距离为 R2(x)=‖Φ(x)-a‖2 (18) 鉴于式(10)和核函数的定义,有 (19) 高维特征空间球的半径为 R={R(xi)|xi是支持向量} (20) 则边界轮廓上的点可以由如下集合定义,即 {x|R(x)=R} (21) 由式(20)可得:支持向量位于类边界上,受限支持向量(BSV)位于类的外部,其它点位于类内。 接下来需要确定每个样本在高维特征空间的类标号,本文采用构造完全图的类别标定方法。具体算法如下: 1)计算特征空间中球体内或球体上的点对xi和xj之间的邻接矩阵Aij,它的元素取值规则如式(22)。其中,i,j=1,…,N。采样方法为随机采样,为了提高算法的速度,一般连续采样10~20个,则 (22) 2)计算Aij对应数据集的联通状态,每个连通分量代表一个类别,采用深度优先算法遍历全部样本,确定每个类别的标号。 3)由于受限支持向量在超球体的外部,因此无法通过以上方式确定它们的类别标号,本文把它们标记为未分类状态。 在构造最优超平面时,决策函数可以看成是支持向量关于核函数的展开式,因而算法的复杂度只与支持向量的个数有关,而与特征空间的维数无关。 数据空间中封闭轮廓的形状由两个参数决定:高斯核的尺度参数q和惩罚因子C。 关于这两个参数选取的问题,一直没有一套全面而系统的理论作为指导,这也一直是支持向量机聚类的一个研究方向,目前在实际应用中多采用经验法或实验法。 由前面的分析可知:在实际操作中,必须要考虑受限支持向量的个数。轮廓分裂点由参数C控制。从式(9)和式(15)可得 (23) 其中,nbsv是BSV的数量。因此,1 /(NC)是BSV数量的下限,设 (24) 当样本数量N比较大时,异常值的比例倾向于p。即当存在不同的类别时,异常值(如由于噪声)会阻止轮廓分离,所以使用受限支持向量(BSV)是非常有用的。由式(23)可得,当C值越小时得到的BSV数量越多。 下面利用支持向量机聚类的方法计算基函数的中心,构造一个RBF神经网络。假设网络的输入样本为X=[X1,X2,…,Xk,…,Xn]T,任意一个训练样本为Xk=[xk1,xk2,…,xkm,…,xkM],k=1,2,…,N。其中,xkm表示第k个样本的第m个输入,RBF神经网络所对应的网络实际输出为Yk=[yk1,yk2,…,ykj,…,ykJ],k=1,2,…,N。 根据得到的基函数中心计算径向基函数的宽度:设其它聚类中心到与第i个聚类中心距离的最小值di,即di=min(‖Ci-Cj‖),按照公式σi=λdi计算各基函数的宽度σi。其中,σ称作重叠系数,用来控制各个径向基函数的平滑程度,重叠系数的值越大,基函数的图像就越平滑。 用梯度法确定RBF神经网络隐含层与输出层之间的权值,其具体实现过程如下: 1)计算核函数矩阵,使用高斯核函数; 2)查找给定约束条件下的拉格朗日乘数、支持向量与异常值,并更正受限支持向量与支持向量的值; 3)计算球体的表达式,采用深度优先搜索算法对对每一个样本点进行类别分配; 4)根据SVM的聚类结果计算每个聚类中心并把它作为每个基函数中心; 5)计算各基函数的宽度σi; 6)训练RBF神经网络,得到网络隐含层与输出层之间的权值。网络权值的计算可以选择代数方法,也可以采用监督训练法,本文采用监督训练法。支持向量聚类的流程图如图2所示。 图2 支持向量聚类流程图Fig.2 Flow chart of clustering based on SVM 基于支持向量机聚类的RBF神经网络的流程图,如图3所示。 图3 基于SVC的RBF神经网络的流程图Fig.3 Flow chart of RBF neural network based on SVC 针对一般神经网络在非线性时间序列预测问题中收敛速度慢的问题,使用基于支持向量机确定基函数中心的方法来改进径向基神经网络实现的动态的建模与预测,并使用该方法对一系列非线性时间序列进行仿真预测。 为了验证改进算法在非线性时间序列预测中的准确性,本部分对黑龙江省1980-2014年的农机总动力进行非线性时间序列预测,并与系统聚类法构建的神经网络的预测结果进行对比。黑龙江省这35年的农机总动力数据如表1所示[9]。 为了避免不同量纲对训练网络的影响,需要对数据进行标准化处理,把原始数据映射到区间[0.2,0.8]上,按照式(25)进行数据的标准化工作。则 (25) 其中,xmin为数据中的最小值;xmax为数据中的最大值。 表1 黑龙江省1980-2014年农机总动力Table 1 The total power of agricultural machinery in Heilongjiang Province from 1980 to 2014 构建训练集数据,假设有M个样本,每个样本的维度为M-N,则一共可以构建N个时间序列。初始化输入维度为6,即以连续6年的实例作为一个输入,第7年的实例作为输出值。按照这种方式构建时间序列,共可以构成35-6=29组数据。选取前25组数据作为训练集,指定后4组数据为测集,让它们与网络的预测效果进行比较。 分别用改进算法和系统聚类的方法训练神经网络,用其预测2011-2014年黑龙江省的农机总动力,然后将预测值与实际值进行比较。预先径向基神经网络的初始参数如下:输入神经元个数为6,输出神经元个数为1,初始权值W0=[1,1,…,1]T,初始阈值b0=1,网络学习精度0.001,重叠系数ε=1,学习率是0.1,支持向量机聚类时的C=1,q=300。采用系统聚类训练径向基神经网络时,网络的各项参数均与改进方法相同。网络的观测值和实际输出值的曲线对比图如图4所示,两种方法具体的输出情况如表2所示。 图4 黑龙江省1986-2014年农机总动力趋势图Fig.4 Trend of agricultural machinery total power in heilongjiang province from 1986 to 2014 表2 实验结果Table 2 Experimental results Table 提出了用支持向量机聚类来确定径向基函数中心的新方法,并给出了这种方法的计算方法及相关模型。将这种方法与系统聚类方法进行对比,分析给出了这种方法的优越性。该方法也不需要预先给出基函数中心的初始点,也不需要预先确定径向基函数的个数,有效提高了神经网络的稳定性和泛化性。通过实验验证了改进的神经网络在提高网络稳定性和提高预测精度等方面的性能。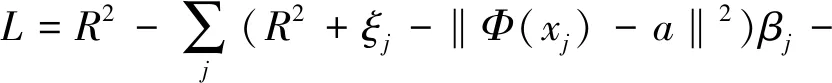
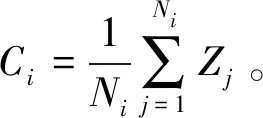
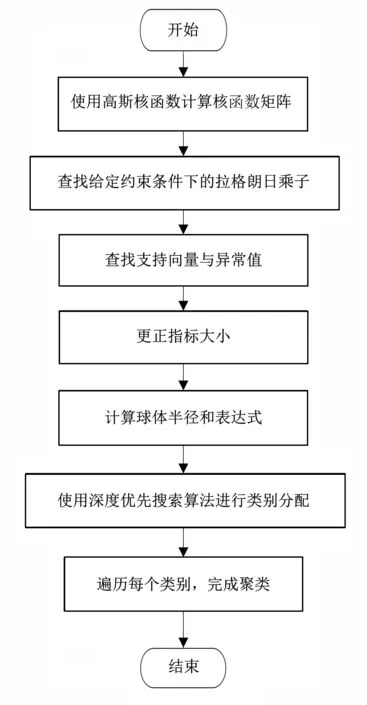
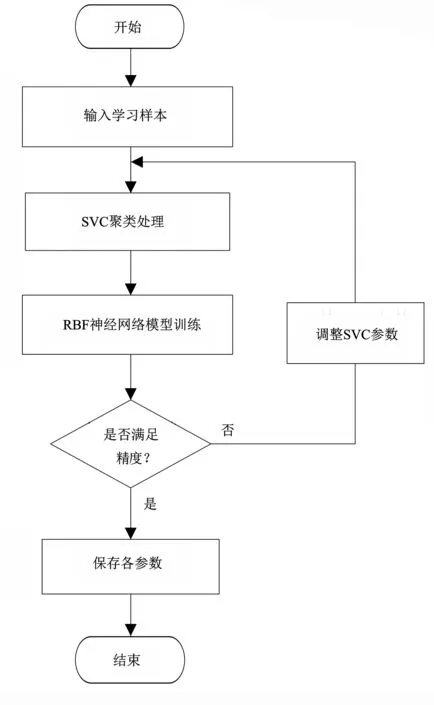
3 农机总动力预测实验
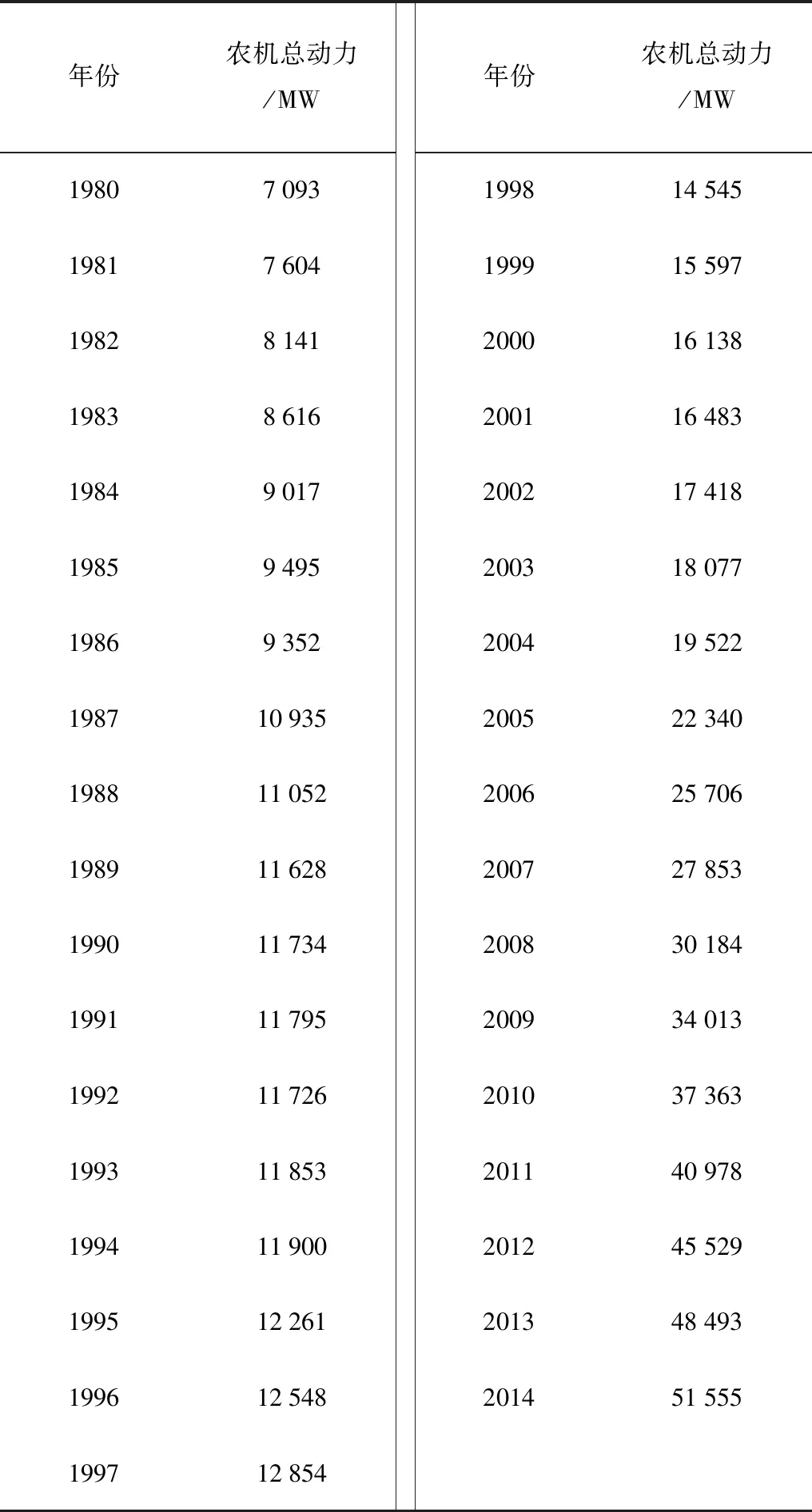
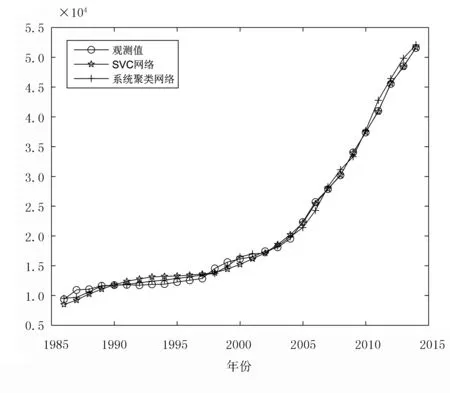

4 结论

