考虑剪胀性的含结构面软岩渐进破损规律研究

刘甫平，周 峙，罗 易

(1.安徽省交通规划设计研究总院股份有限公司，安徽 合肥 230088；2.公路交通节能环保技术交通运输行业研发中心，安徽 合肥 230088；3.中国地质大学(武汉) 工程学院，湖北 武汉 430074)

软岩在漫长的沉积历史过程中，伴生许多弱胶结的原生结构面(带)，是一种具有显著塑性变形的非均匀介质。其峰后塑性应力应变特征一直是岩土工程关注的焦点，提出适用于软岩的力学本构模型，不仅有利于其结构参数确定和峰后应变软化规律的预测，也能指导软岩地区巷道支护、井壁稳定性等工程的设计。

传统塑性力学理论框架内，对于连续均匀介质的剪切屈服只考虑服从德鲁克塑性公设[1-2]，其球张量只产生球应变，偏张量只产生偏应变。而在岩土塑性力学范围内，岩土是一种不均匀的多相颗粒体，其球张量和偏张量存在交叉影响，宏观上表现为剪胀或剪缩。因此，严格来讲，对于不均匀介质的材料微元不宜采用连续材料微元，而宜采用更能反映变形过程中颗粒相互影响的细观力学模型更为合理[3](P8)。

沈珠江院士在岩土破损力学框架下提出的二元介质模型[4]，将不均匀介质微元抽象为胶结元和摩擦元，前者表现为脆弹性，后者则表现弹塑性特征。当单元体受外部荷载作用时，黏聚力和摩擦力并非同时发挥作用[5]，而是前者破坏后，后者才逐步发挥抗力，在此过程中会出现岩土材料的应变硬化-软化，破坏过程也可以抽象的认为胶结元逐步转化为摩擦元的过程，该过程能够考虑被结构带切割的体元之间的摩擦咬合作用对材料整体强度的贡献，比传统的塑性力学研究更接近于实际。

自二元介质模型提出以来，刘恩龙、陈铁林等学者通过二元介质模型在超固结黏土、黄土、堆砌体、冻土等结构性土的研究[6-9]，验证了模型可以较好地反映结构性土的应力应变特征。而软岩材料与结构性土具有相似的应力应变行为，但是目前在岩土破损力学理论框架内，有关软岩在加载进入塑性状态后的变化规律研究却较少，多数岩样的二元介质模型均以硬质岩为例进行验证[10-12]。文献[11]提出单元体在破损前后弹性模量、泊松比均相同，只是单元体的破裂强度满足Weibull分布探究了砂岩破损函数的演化规律，并分析了参数选取对峰值强度、应变软化的影响，模型能定性的反映砂岩的峰后软化规律，研究主要集中于破损函数的演化规律。随后刘恩龙在沈珠江院士的研究基础上，将硬化参量引入破损过程中摩擦元的应力应变关系[12]，基于剑桥模型给出了摩擦元的流动规则，并基于常规砂岩的三轴试验验证模型的合理性，研究虽然基于剑桥剪胀方程考虑了摩擦元的塑性流动规律，但是从p-q平面上看，对于颗粒类材料的剪胀线应该是非线性的，那么这就会导致模型对岩样在塑性屈服后的剪缩-剪胀反映不足。而对于软岩而言，其相比硬岩更易在塑性屈服阶段表现剪胀(扩容)现象，因此如何提出适用于软岩变形特征的二元介质模型十分重要。

基于此，本文在岩土破损力学的理论框架内，将含结构面的软岩中胶结强的结构单元抽象为弹脆性元，满足广义虎克定律。将软弱结构面抽象为摩擦元，在满足Mohr-Coulomb准则基础上，确定塑性剪应变为塑性内变量，采用非关联流动法则获取摩擦元的剪胀角，并引入剪胀比表征摩擦元剪胀规律，以此建议了一个能反映含结构面软岩的应变软化过程的增量型二元介质本构模型，最后在MATLAB中进行增量计算，并与含结构面的粉砂质泥岩进行三轴试验结果对比，表明所建立的本构模型能合理的描述含软弱结构面软岩的应力应变特性。

1 基本假定与二元介质模型一般关系

1.1 基本假定

2002年，基于结构性土的细观破损机理，沈珠江院士提出了岩土破损力学的理论框架[13]，并提出了以下假定：

1)准连续介质假定，即在二元介质中任意选取一个代表性单元(RVE)，其包含多个胶结块和结构面；

2)脆弹性破损假定，即结构脆弹性元一旦满足破坏准则立即发生破碎。

3)共同分担假定，宏观应力由结构块胶结应力和软弱带的摩擦应力共同分担，满足以下关系式

其中[σ]i、[σ]f分别为平均胶结应力(弹脆性元)与平均摩擦应力(弹塑性元)，[ε]i、[ε]f分别为平均胶结应变、平均摩擦应变、ζv为体积破损率。

1.2 二元介质模型一般关系

非均匀介质的均匀化理论根据参数关系不同，可以分为单参数均匀化理论和双参数均匀化理论。单参数均匀化理论认为RVE中的胶结元破损过程中转化为摩擦元时，其球应力与体应变均按体积平均。而含结构面的软岩在进入软化塑性状态后，常沿某一结构面发生破坏，那么局部应变会在结构带附近出现，因此比较合理的将球应力与体应变按体积平均，剪应力与剪应变按面积平均，定义双参数表征均匀化，即体积破损率ζv、面积破损率ζs。

分别定义[σ]m、[σ]s分别为球应力和剪应力，分别用下标i表示胶结元、下标f表示摩擦元。

软岩进入塑性变形阶段，由于加载、卸载时的规律不一样，其应力-应变不再具有唯一对应关系，因此，对弹脆性元和弹塑性元分别采用增量型应力应变关系表述：

由式(2)、(4)可知RVE的平均应变增量主要由弹脆性元的应变增量、弹塑性元的应变增量及弹脆性元破损转变位弹塑性元引起的应变增量组成，后文对此进行详细阐述。

2 考虑剪胀特性结构面软岩的二元介质破损模型推导

2.1 弹脆性元(胶结元)本构关系

假定胶结元破损前为理想弹脆性体，则其满足广义虎克定律：

Ki、Gi分别为弹脆性元的体积模量和剪切模量。

2.2 考虑剪胀角弹塑性元(摩擦元)本构关系

对于摩擦元，根据脆弹性破损的基本假定，当结构块一旦满足破损准则，那么将胶结元丧失胶结强度立即转化为无黏性颗粒，表现为滑移特性(摩擦强度发挥阶段)。

此时胶结元转化为摩擦元过程可以用理想塑性材料的弹塑性的应力应变特性进行描述，对于常规三轴试验，屈服函数可按Mohr-Coulomb屈服准则，其应力点在π平面应该为两条棱线[14]，因此可以表示为：

其中，Nφ为内摩擦角的函数，Nφ=(1-sinφ)/(1+sinφ)。

在颗粒受剪切过程中，会出现颗粒的翻转、破损从而导致显著的剪胀现象。目前常用剪胀角表述剪切变形过程的体胀过程，但是在考虑剪胀的过程中存在两种较为常见方式，其一采用非关联流动法，使得Ψ=0，其实是忽略了颗粒的剪胀性，其二是采用屈服函数作为塑性势函数的关联流动法则，使内摩擦角与剪胀角为定值，这就高估了材料的剪胀性。基于此，本文采用非关联法则，同时将屈服函数的内摩擦角替换为剪胀角Ψ来研究摩擦元的剪胀特性。将内摩擦角替换为剪胀角Ψ塑性势函数可以得到：

式中Nψ为剪胀角Ψ的函数，Nψ=(1+sinψ)/(1-sinψ)。由于岩土材料一般发生剪切屈服，本文以等效塑性剪应变为内变量，采用非关联流动法则，求出剪胀摩擦角Ψ的表达式，

(16)

当胶结元破损形成摩擦元过程中出现剪胀时，会出现临胀特征点，定义剪胀应力比Md表示，该点对应的摩擦角Ψ0定义为临胀摩擦角。采用剪胀比(塑性体应变与塑性剪应变的比)表示摩擦元塑性流动规律，即：

式中dg为剪胀比，υ为剪胀模型常数，与材料性质相关，η=σs/σm，其变化范围为(0，1)。

可以用文献[12]关于岩石的二元介质模型表征结构面软岩摩擦元的增量型应力-应变关系：

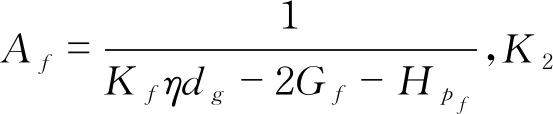
那么有

将式(21)与(22)代入(11)、(12)式，并定义胶结元和摩擦元的刚度系数分别为D1、D2，则有

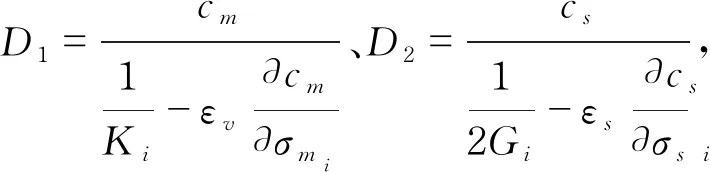
将式(23)、(24)联立式(11)、(12)，可得

将式(27)、(28)代入(25)、(26)，整理可得

那么式(19)、(20)可以写成

根据式(27)、(28)、(31)、(32)分别代入式(7)、(9)可以得到含结构面软岩的二元介质模型如下：

含结构面软岩的二元介质本构模型中有5组参数需要确定，对于胶结元，分别为弹性体积模量Ki、弹性剪切模量Gi；对于摩擦元，分别为弹性体积模量Kf、弹性剪切模量Gf；结构破损参数中体积破损率ζv、面积破损率ζs，局部应变系数cm、cs；临胀特征点的剪胀摩擦角Ψ；后文将分别阐述模型参数的演化规律。

3 二元介质模型渐进破损过程及参数确定

3.1 结构面软岩二元介质模型渐进破损过程分析

结构面软岩渐进破损可以划为三个阶段，分别为弹性变形阶段、硬化-软化阶段(胶结元转化摩擦元)、残余阶段(胶结元完全破损摩擦元滑移)，如图1所示。

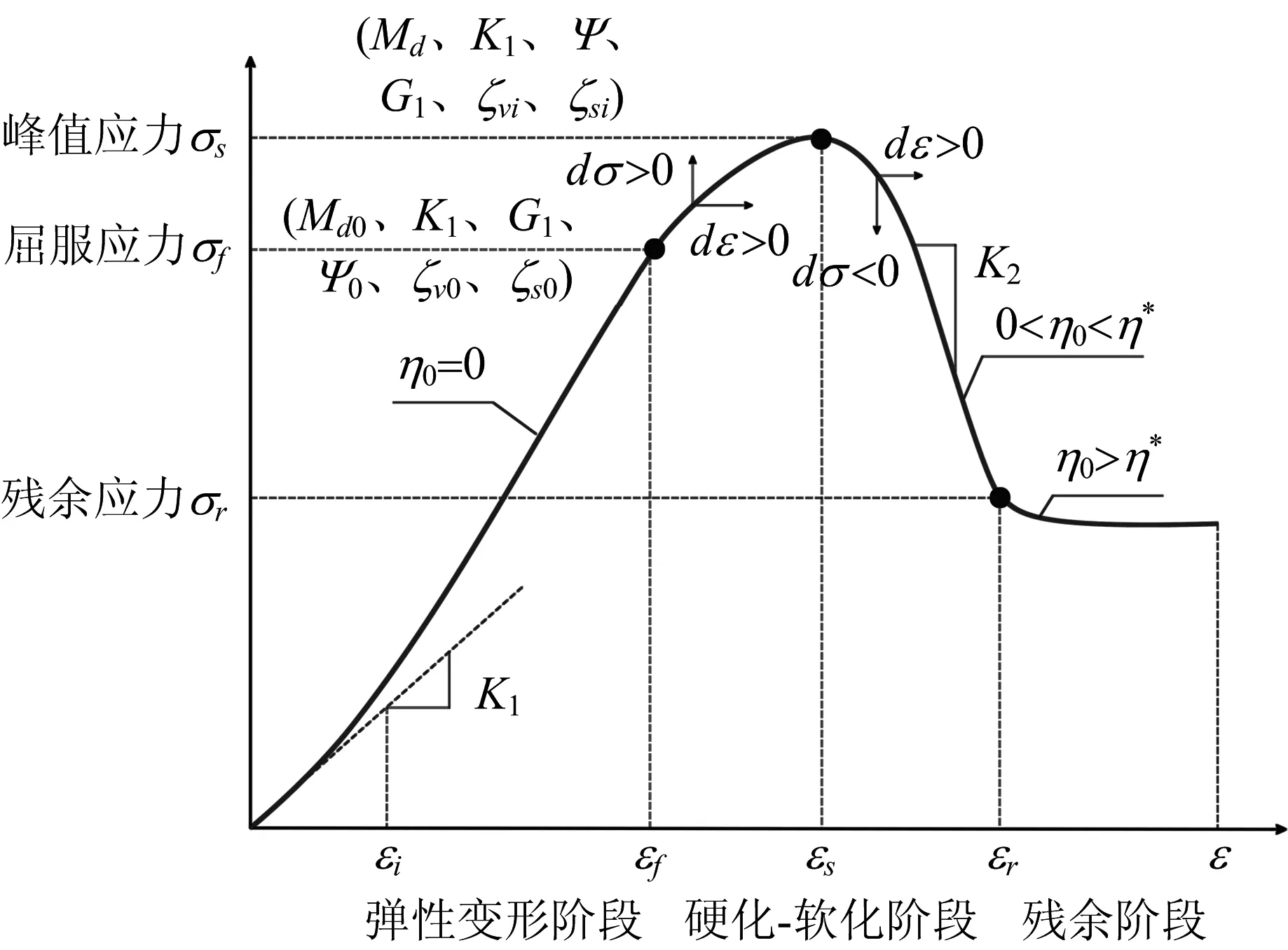
图1 二元介质模型渐进破损过程

当试样达到屈服应力σf之前，η=0时，该阶段认为外部荷载主要由胶结应力承担，处于线弹性变形阶段；

当0<η<η*时(η*为胶结元从应变软化转变到残余阶段的临界软化参数，由残余应变与峰值应变的比确定)，表示胶结元达到初始破损门槛值(即为屈服应力)后，试样开始表现出剪胀(缩)现象，该阶段胶结元开始转化为摩擦元，外部荷载由胶结应力及摩擦应力共同承担，该阶段在应力-应变曲线上表现为应变硬化-软化(剪缩-剪胀)；

当η>η*时，无胶结强度的摩擦元滑移，表征胶结元完全转化为摩擦元的残余阶段。

3.2 弹性参数确定

胶结元Ki、Gi可以用不含结构面的岩样的三轴剪切试验应力应变曲线(σ1-σ3)-ε1的初始斜率获取。

摩擦元的弹性体积模量和剪切模量根据峰后应力-应变曲线按下式确定：

式中μf为摩擦元的泊松比，Pa为标准大气压强，为101 Kpa，σc为残余强度。

3.3 破损参数确定

3.3.1 初始破损门槛值变化规律

结构面软岩不同于结构性土，单纯围压作用下不会引起胶结元的破损，因而胶结元的破损应达到其初始破损应力门槛值才会发生。随着轴向荷载的增加，应力应变关系开始呈非线性变化，应变变化较快，在应力差的对数坐标中显示尤为突出。在结构面软岩峰前应力-应变曲线中存在应变陡增转折点，即为结构面软岩的初始破损点，对应初始破损门槛应力。

限于篇幅，本文仅列出σ3=1.0 Mpa的ln(σ1-σ3)-ε关系图，如图2所示，对应的不同围压的初始门槛应力值见表1。

图2 初始破损应力差对数-轴向应变关系曲线

σ3(MPa)qe(MPa)σ3(MPa)qe(MPa)0.510.51.514.21.011.62.016.4

3.3.2 结构破损参数变化规律

岩石内RVE单元体的胶结元的局部应力达到破损门槛值时即发生破损，胶结元逐步转化为摩擦元，这个过程中体积发生膨胀，同时会出现破损带，因此，破损率范围值从0逐渐变化至1[15]，如图3所示。

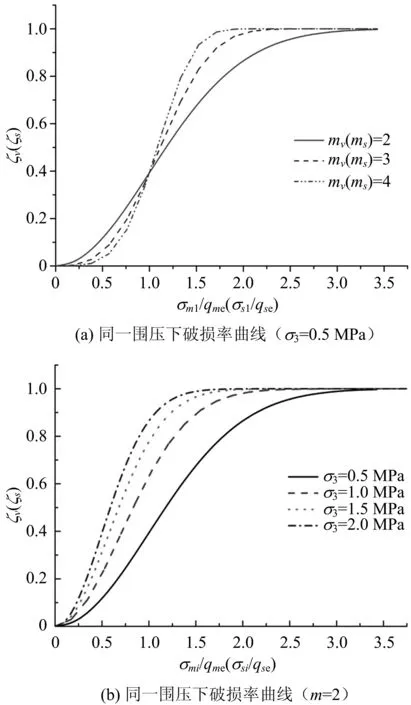
图3 破损率曲线

对于岩石而言，假设破损率满足Weibull分布[14]，按如下关系式表示：

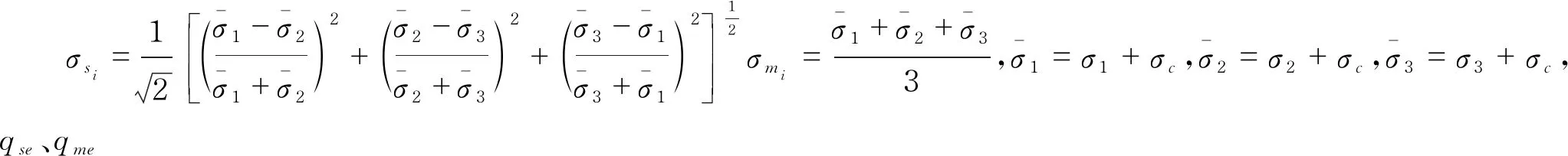
m值的选取与结构面软岩的材料性质和结构面胶结程度有关。m值愈大，破损率变化愈快，峰值强度愈低，岩石更易发生破损，本文建议胶结强度高的岩石模型m值取小值，对于弱胶结的岩石取大值。局部应变系数cm、cs也是无法直接量测，可通过先假设，后试验验证的方式间接确定。cm、cs为应力的函数，那么可以构造下列表达式，

其中αv、αs分别为模型参数，通过选取拟合可以求得。此处通过将式(35)、(36)、(37)、(38)代入(33)、(34)中通过与试验曲线对比可以确定m、αv、αs参数值。

3.4 剪胀参数规律

根据三轴试验εv-ε1曲线进行整理，获取塑性体积应变与轴向塑性主应变与等效塑性剪应变的曲线最优化拟合关系，并分别对塑性体积应变、轴向塑性主应变微分，给定一个等效塑性剪应变的增量步，可以求得不同等效塑性剪应变下的剪胀角Ψ，以此获得胶结元转化摩擦元过程中的剪胀比。

以1.0 MPa围压下的塑性体积应变与轴向塑性主应变与等效塑性剪应变的曲线最优化拟合关系为例进行阐述，如图4所示。塑性体应变增量和塑性轴向应变增量可以用等效剪应变增量表示为：

代入式(16)可知

图4 塑性轴向应变、体积应变与等效塑性剪应变关系图

屈服应力对应的等效塑性剪应变可以得到临界剪胀角，代入公式(17)、(18)及本构关系(33)、(34)确定dg并与试验曲线进行对比，选取最优模型参数υ。

表2 本文计算采用临胀角

根据式(18)分别计算应力比与剪胀比的关系，同时与Rowe剪胀方程和剑桥剪胀模型计算结果对比，以1.0 MPa下的试验数据为例进行对比分析，不同剪胀参数规律如图5所示。

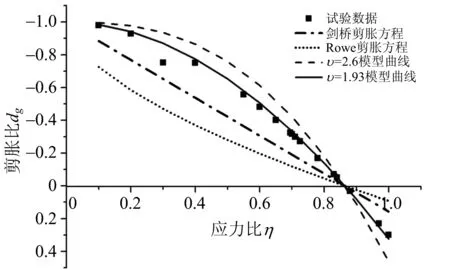
图5 不同剪胀参数规律(σc=1.0MPa)

摩擦元在破损过程中应力比与剪胀比的关系应该是非线性的[16]，而剑桥剪胀方程为线性关系，并不能很好的反映剪胀性。而Rowe剪胀方程所表述的剪胀关系则明显低估了摩擦元的剪胀性。采用本文的剪胀比模型与试验结果拟合较好。同理可以求得其他不同围压下的剪胀比和最优的剪胀模型参数υ。

4 模型的验证

试验岩样为弱风化含青色泥质结构面的紫红色粉砂质泥岩，天然密度2.63 g/cm3。试样尺寸为∅50 mm×100 mm的圆柱形岩样，常规三轴试验采用中国地质大学岩石力学实验室的INSTRO微机控制岩石伺服三轴压力试验机，采用位移控制加载方式，加载速率0.002 mm/s，分别对试样进行围压为0.5 MPa、1 MPa、1.5 MPa、2.0 MPa的三轴剪切试验，破坏形式如图6所示，并与理论计算结果进行对比。

计算采用的模型参数Ki=4.197 GPa、Gi=1.800 GPa，μf=0.18， 改变围压的情况下可求得不同围压下的Kf、Gf，mv=2，ms=2，αv=0.001，αs=200，围压为0.5 MPa、1 MPa、1.5 MPa、2.0 MPa的剪胀模型参数υ分别为1.93、1.51、1.34、0.92，η=0.7，在MATLAB中编程实现模型增量计算，首先设定一个加载步，给定一个微小的dεv、dεs、dζv、dζs，在摩尔-库伦准则下判定是否屈服，满足屈服条件后记录当前应力状态，并根据非关联流动法则计算等效塑性剪应变增量和剪胀角，由于破损率ζ本身是局部应力函数，局部应变系数cm、cs也是局部应力的函数，如若考虑每个增量步中两者相互转化，求解非常复杂，本文假定每个增量步中cm、cs不变，按上一步ζv、ζs增量计算ζ，以此求得每个单元弹性应变增量和塑性应变增量，如此不断给定加载步，即可求出不同围压下的偏应力-轴向应变曲线和体积应变-轴向应变曲线，对比计算曲线与试验曲线后迭代给出ζv、ζs、cm、cs，不断优化计算结果，数值计算结果与试验结果对比如图7所示。建议的模型与试验曲线拟合较好，可较好地反映含结构面软岩屈服后的应力-应变关系，在低围压下，随着应变的增加，试样表现较强的应变软化现象(剪胀)，随着围压的增大，剪胀逐渐变弱。

图7 模型计算结果与试验结果对比

5 结论

1)在岩土破损力学理论框架内，将含结构面软岩抽象为胶结元和摩擦元的非均匀介质，认为两者在破损规律下相互转化，相互影响，能反映岩石单元体体应力与剪应变、偏应力与体应变的交叉影响关系。

2)基于摩尔-库伦准则和非关联流动法则，并以塑性剪应变为内变量，将剪胀比引入二元介质破损模型中考虑摩擦元破损过程中的剪胀性，从而更能反映单元体渐进破损过程中的应变硬化-软化特征。

3)结构面软岩的破损不同于黄土、松砂、结构性土，单纯围压作用下不会引起胶结元的破损，因而胶结元的破损应达到其初始破损应力门槛值才会发生。

4)增量计算结果与常规三轴试验结果进行对比分析，发现建议的模型可以较好地反映含结构面软岩的应力-应变特征。提出的模型是在试验基础上建立的，为类似性质岩石提供借鉴。

本文仅对低围压水平下的软岩进行了试验和模型验证，以后需加强模型在高围压应力水平下的剪胀特性验证。