典型姿势下上肢操作力限值与关节角的研究
陈汉青,郝建平,李智猛
(陆军工程大学石家庄校区,石家庄 050000)
1 引言
人类工效学是研究如何统一考虑工作效率、人的职业健康、工作安全和舒适性等问题的学科[3]。论文以维修操作力量为对象,进行了侧蹲姿势下维修人员上肢操作力量限值实验;分析了不同关节角对于上肢最大力的交互作用关系;通过正交实验结果的分析,筛选了上肢最大力的显著性影响因素;在此基础上,测量出显著性影响因素组合下的力量限值;建立了具有可信性的侧蹲姿势下上肢维修操作最大力回归模型,获取维修操作力的基础数据以及不同工效因素对于人体力量的影响关系,为设备的维修性设计提供参考。
2 对象与方法
2.1 维修姿势的一般分类方法
姿势可理解为人在作业时身体部位所呈现的一种几何状态组合[4]。维修人员姿势是影响维修工效的一个重要因素,这不仅包括躯干的状态,还包括直接操作装备的身体部位(通常为上肢)的状态,本文主要选择上肢的姿势。
上肢动作由上肢关节的运动来完成的,包括肩关节、肘关节和腕关节。根据人体解剖学对于关节自由度的描述,人体上肢可以简化为一个七自由度的刚体模型[4],其中,α 为肩关节内收/外展角、β 为肩关节屈/伸角、γ 为肩关节外旋/内旋角、δ 为肘关节屈伸角、θ 为肘关节旋角(小臂旋角)、μ 为腕关节内收/外展角、ρ 为腕关节屈/伸角。
但由于肩关节的内收和伸展并不符合维修中的人体操作习惯,因此,在实验中,α 指肩关节外展的角度,β 指肩关节屈曲的角度。
在GJB/Z 131 -2002《军事装备和设施的人机工程设计手册》[5]中处理上肢关节角最大活动范围如表1 所示。
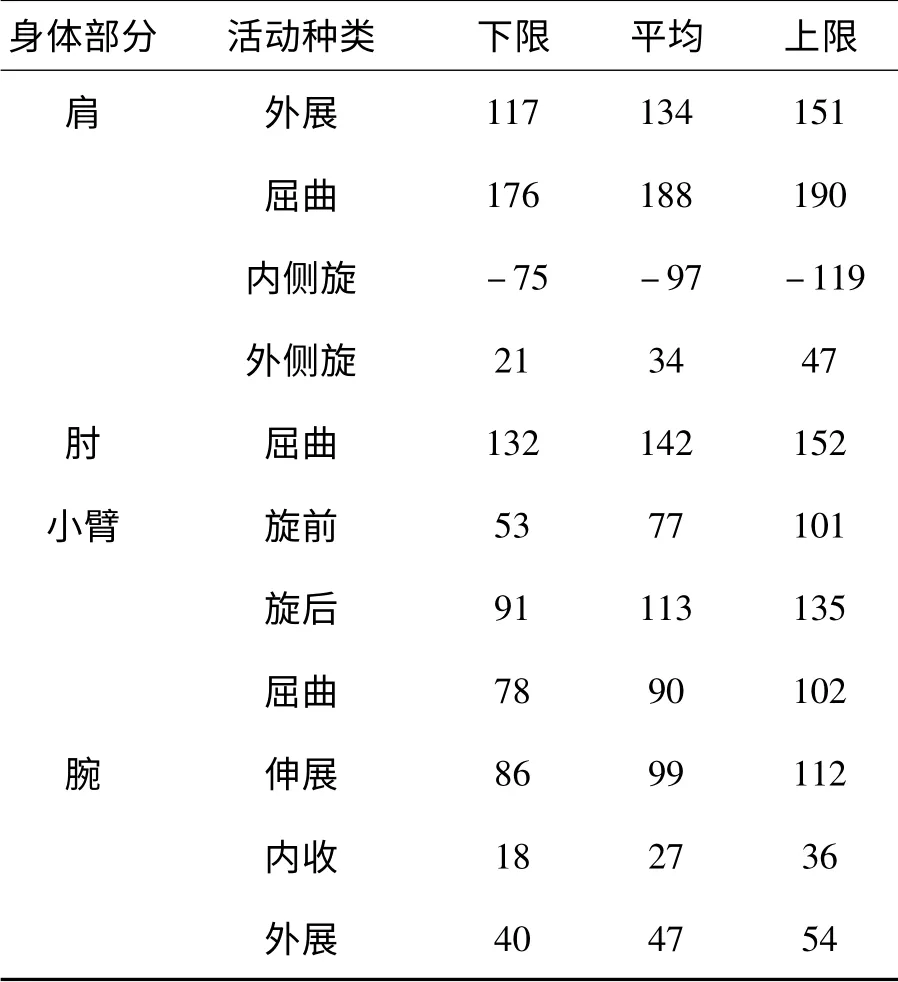
表1 上肢关节角最大活动范围
上述最大活动范围为裸体人员的测量结果,该标准里额外指出,在方便操作和维修时,应该采用下限,因此,本研究中取下限活动范围角度作为七个关节的最大活动范围,整理如表2所示。
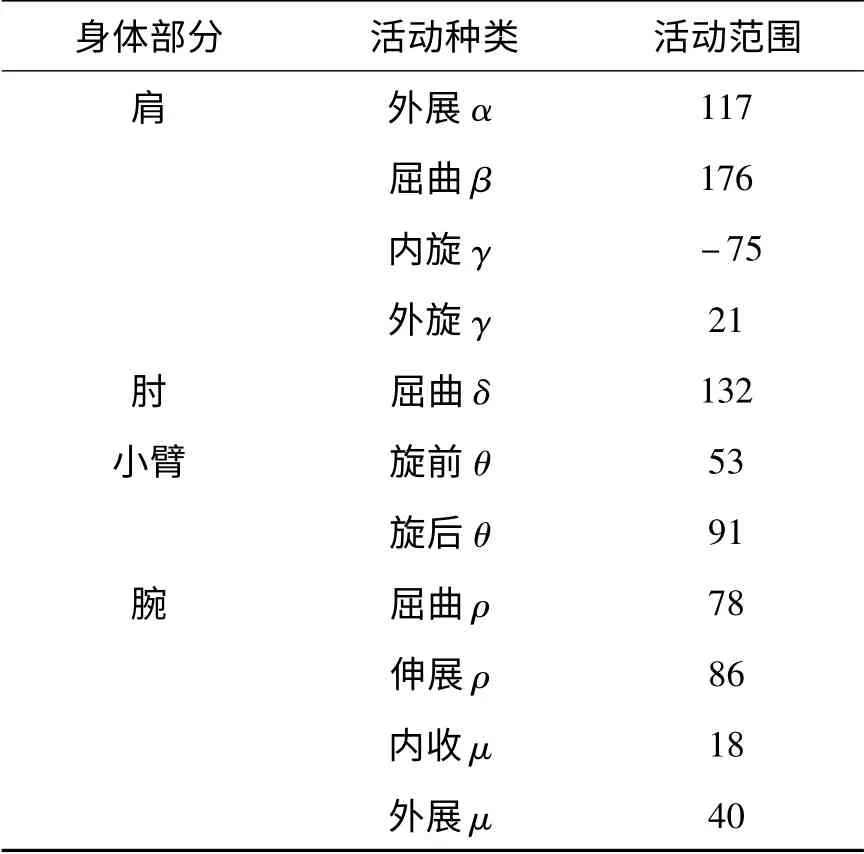
表2 维修操作上肢关节角最大活动范围
2.2 试验关节角的选取
首先按照维修工效分析表,结合实际维修动作,挑选出几个对于操作施力影响不大的关节角,并使用测量设备对其进行筛选性最大力测量,最终确认出对于上肢最大力的影响不明显的关节角,并将其剔除,从而将显著影响维修操作力量的上肢关节角划定为五个,分别是肩关节内收/外展角α、肩关节屈/伸角β、肩关节外旋/内旋角γ、肘关节屈伸角δ、腕关节屈/伸角ρ 见图1。

图1 手臂七自由度关节模型
2.3 试验设计
2.3.1 试验设备
实验力量测量设备采用BTE Primus RS 运动测量评估系统,该系统可实现对各类复杂动作的模拟,实现实际作业情况与实验室的对接,采集作业活动中的力量数据,用于对维修工效中力的测定以及力的时间关系的测量,其外形如图2所示。

图2 BTE Primus RS 运动测量评估系统
2.3.2 侧蹲姿势上肢最大力显著性影响因素筛选实验
在对维修操作影响因素水平筛选之前,首先要考虑筛选的方法,方法本身应该既要工作量适中,又能给影响因素水平筛选带来便利。本次显著性影响因素筛选实验采用正交实验。
(1)正交实验因素及其水平
由于实验的目的是研究侧蹲姿势下的工效问题,我们选取侧蹲姿势所提供的最大力。根据人类工效学原理,本文将人体划分为一个刚体模型。侧蹲姿势下上肢的复杂多变决定了各个关节角组合较多,而且各个角度的变化范围不统一,本部分就这5 因素给出水平划分值。各因素水平表如3 所示,其中为了方便表示,肩关节的内旋角度取正值,外旋角度取负值;腕关节伸展角度取正值,屈曲角度取负值;腕关节内收角取正值,外展角取负值。

表3 特殊姿势下最大力显著因素筛选正交实验因素与水平
(2)在因素间交互作用显著性判断实验中,因素自身对于实验结果有各自不同的影响,如果因素与因素之间结合后对实验结果还会产生影响,那么这种结合后的影响就称之为交互作用。在正交实验设计时,因素之间的交互作用会影响到正交表头的设计,影响实验结果。因此,在设计正交表头时,必须对因素之间交互作用的有无作出判断,如果交互作用显著,则该交互作用作为一个额外的因素考虑,如果不显著,则不予考虑。
在多个因素的实验中,交互作用的显著性主要依靠经验进行判断,当主观经验不能确认交互作用的显著性时,则需通过实验来进行分析[6]。
为使交互作用关系的结果更为准确,本实验专门针对因素之间交互作用的影响关系做了实验分析。本次实验采用控制变量法,固定三个角度,研究其他两个角度在相互作用时,最大力量变化规律。
此外,需要指出的是,实验中固定三个角度时,如果没有特殊说明,采用这个角度的中间水平,而没有遍历所有的角度范围,原因就在于所需要得到的交互作用关系为定性关系,如果其余两个因素之间存在交互关系,那么就可以在这种设计的结果中体现。这样的设计方案能解决所研究问题,且工作量相对较少。
实验中共涉及5 个因素,因素间两两结合,共有C2
5 = 10 种。每种组合下测量最大拉力,最终形成交互作用判断数据及相应的直观分析图,现选取其中有交互作用和无交互作用各一例作说明。

表4肩关节外展角和肩关节屈曲角组合下的拉力统计表
将表4 中数据利用Excel 绘制成折线图,作为交互作用判断的直观分析图。按照统计学理论,如果图中的三条线存在明显交叉,则可判定两个因素之间是存在交互作用的。图3 中,三条线存在明显交叉,因此,肩关节外展角和肩关节屈曲角对于上肢最大拉力存在交互作用,在正交实验中,应当增加α 与β 的交互作用列。
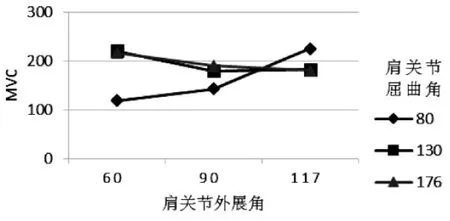
图3 肩关节外展角和肩关节屈曲角组合下的拉力折线图
在直观分析图中,当表中的折线平行或近似平行时,可认为两个因素之间不存在交互作用或交互作用不明显,可以忽略,例如,肩关节外展角α 和肩关节旋角γ 组合下的拉力结果如表5 所示。
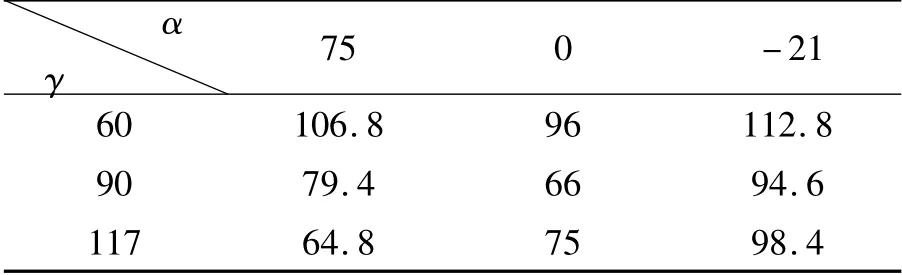
表5肩关节外展角和肩关节旋角组合下的拉力统计表
将其结果绘制成折线图,如图4 所示。交互作用列(α × β)1和(α × β)2。
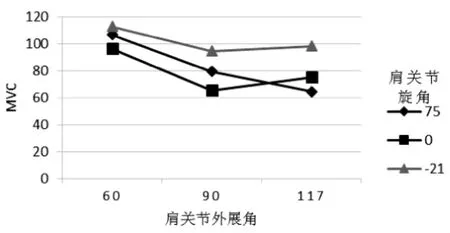
图4 肩关节外展角和肩关节旋角组合下的拉力折线图
3 试验结果
按照正交表的实验号,共有二十七个测试点,其中每个测试点对应一个上肢姿势。每个测试点进行扭力最大力量的测试,最终的实验方案及结果如表6。

表6 最大力显著性影响因素筛选实验方案记录
(1)极差分析。首先进行不同因素水平影响下最大推力的极差分析,结果如表7 所示。其中Kj表示因素列中水平号为j 的所有实验结果之和;kj= Kj/s,其中s 为与每个因素中各水平出现的次数;Rj称为极差,在不同因素列上:
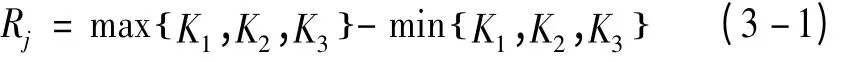

表7 侧蹲姿上肢关节角最大拉力的极差分析
通过对侧蹲姿中最大拉力的极差分析,可以直观的看出五个影响因素的主次关系排序为α>δ >ρ >γ >β,且β 因素的极差要明显小于其他因素,为显著性较差的因素。
(2)方差分析。由于极差分析没有将因素引起的改变与实验误差引起的改变作对比,也没有对因素影响的显著性进行分析,存在不足,因此继续用方差分析筛选出显著性影响因素。
设正交实验的水平数为r,列数为m,总实验次数为n,实验结果为yi(i = 1,2,3,…n),下面按照方差分析的步骤对侧蹲姿最大拉力进行分析:
1)计算偏差平方和
①总偏差平方和

总偏差平方和

②各因素的偏差平方和

其中ki为因素所对应的k 值。
③交互作用的偏差平方和

④实验误差的偏差平方和
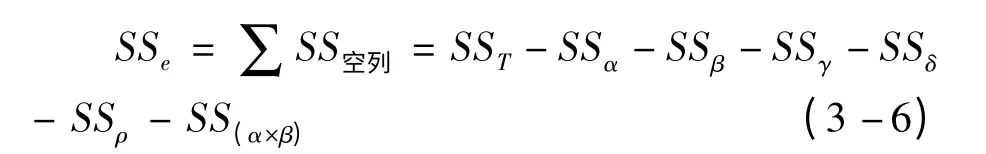
2)计算自由度
总自由度:

各因素自由度:

α 与β 交互作用自由度:

误差自由度:
dfe= dfT-(dfα+dfβ+dfα×β+dfγ+dfδ+dfρ)(3 -10)
3)计算均方

4)计算F 值

借助数据分析软件Minitab 对上述关节角度对于最大拉力的影响因素进行方差分析,结果如表8 所示。根据F 值计算结果对于显著性水平0.05,肩关节外展角α,肘关节屈曲角δ、腕关节屈伸角ρ、肩关节旋角γ 对于最大力有显著性影响;肩关节屈曲角β 对于最大力没有显著性影响,各因素显著性排序为α >δ >ρ >γ >β,与极差分析结果相一致。
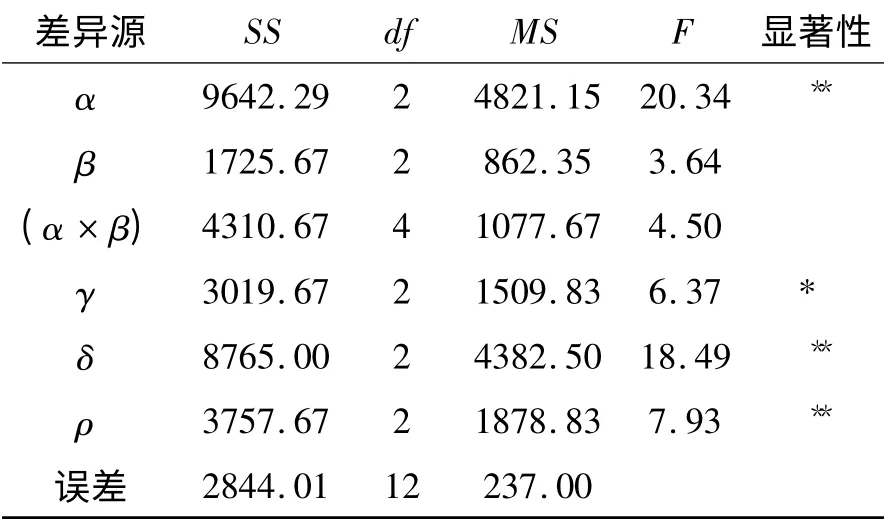
表8 侧蹲姿上肢关节角最大拉力方差分析
综上所述,侧蹲姿中最大旋力显著性影响因素筛选结果为肩关节外展角α,肘关节屈曲角δ、腕关节屈伸角ρ、肩关节旋角γ。
(3)侧蹲姿上肢最大拉力全面实验数据分析
根据全面实验的结果,借助SPSS 软件进行回归分析,假定回归关系为多元线性回归,进行回归拟合,分析结果界面如表9,表10,表11所示。

表9 模型汇总
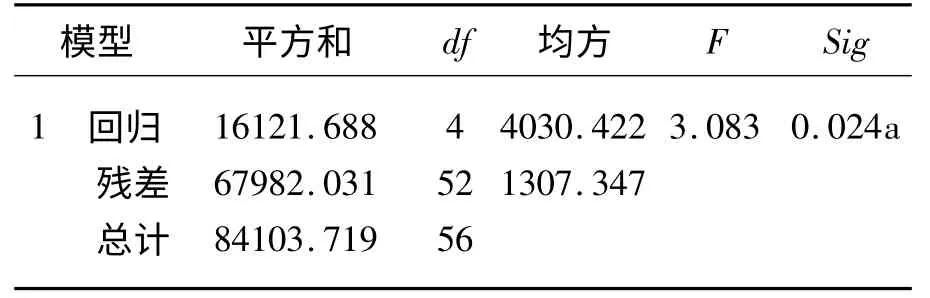
表10 Anovab

表11 系数a
根据SPSS 拟合系数的结果,确定最终四个关节角度对于最大推力的四元线性回归方程:
F拉力max= 159.453 + 0.190α - 0.293δ -0.206γ -0.025ρ
为了判断上述回归方程的可信性,对上述回归方程进行F 检验,对回归系数进行t 检验。
(4)回归方程F 检验
最终的方差分析结果如表12 所示。
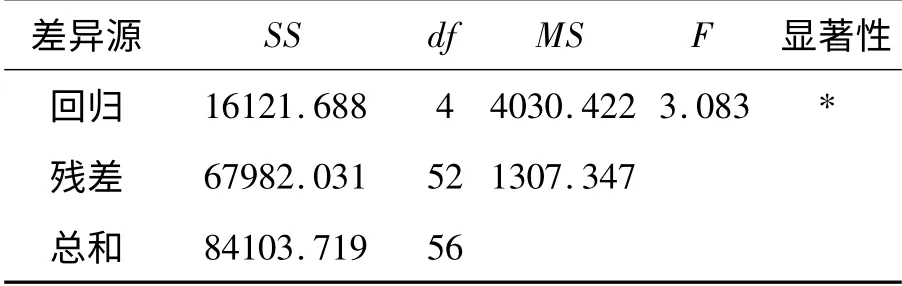
表12 侧蹲姿最大拉力实验多元线性回归方差分析表
对于显著性水平0.05,通过Excel 软件中的FINV 函数生成F 分布表,得出F0.05(4,52)= 2.54,F >F0.05(4,52),因此,上肢最大拉力与四个关节角度间具有显著的线性关系,回归方程可信。
(5)回归系数t 检验
为了判断回归方程中自变量对于因变量影响的显著性程度,对方程中的回归系数进行t 检验。
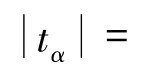
4 讨论
(1)针对关节角众多且对于极限力量影响显著性存在差异的特点,首先使用正交实验的方法,进行模拟侧蹲姿的维修操作力量限值测量,筛选出显著性影响因素;而后,使用全面实验方法,对于力量限值作进一步测量,得到了不同因素组合下上肢极限力量数据。在此基础上,建立力量限值与关节角度之间的回归方程,经过检验,回归方程具有显著的线性关系,回归方程中的因素对于实验结果都有显著性影响,回归方程具有较高可信度。
(2)丰富装备维修性关于工效的基础数据
工效学基础数据的应用几乎涉及人类活动的所有领域,与人们的生活息息相关,所有供人使用的产品和环境都应考虑“人”的生理特点和能力限制,因此,工效学基础数据不仅是工效学研究的基础,也是一个国家的基础性数据资源,对国家的科技进步、经济与社会发展具有重要的支撑作用。在我国装备维修领域,维修工效基础数据十分缺乏,对于一些装备非典型姿势的维修数据基本没有,对于维修工效模型的研究缺少必要的工效基础数据支持,因此本研究可以丰富装备维修性关于工效的基础数据。
(3)提高数字样机维修性技术的应用效果
针对当前国内基于Jack 等商业软件研制的人机工效仿真分析应用系统的基础人机工效数据与标准不符合国内人体情况,利用本研究中工效试验的基础数据结果,可以对维修工效仿真分析工具进行改进,维修典型动作基础数据可以作为虚拟仿真软件的输入,更加符合维修实际情况,从而提高数字样机维修性技术的应用效果。
(4)为装备维修性设计准则制定、设计分析、设计核查等提供数据参考
装备的维修性设计要考虑维修人员在给定工况下的操作力量限值因素以及重复操作产生的疲劳因素,尽量提供人体更容易施力的工况,避免一些不良姿势,保证维修人员的操作负荷能力满足拆卸、安装的力量要求,本研究中的工效基础数据就可作为设计过程中的参考,避免由于高估人体操作负荷能力,造成维修人员完不成给定作业,或者低估人体操作能力而投入多余的设计。
5 结论
从关节角的显著性因素筛选到利用SPSS 分析得出结论一致,对于上肢侧蹲姿最大拉力影响程度分别为:肩关节外展角、肘关节屈曲角、肩关节旋角、腕关节屈伸角。本结论可以对维修性设计时提供参考,在进行设计某些维修活动时,可以按照影响程度进行设计,充分考虑关节角对上肢最大力的制约,从而更好的分析功效数据。同时在对维修人员的保护上也可以按照影响因素进行设计,对影响因子较大的关节角提供更好的保护,从而达到维修工作效率、健康与安全以及舒适程度的有机统一。

