基于ATSUKF算法的卫星姿控系统故障估计

陈雪芹，孙瑞，吴凡，蒋万程

哈尔滨工业大学 卫星技术研究所，哈尔滨 150080

增广状态估计法常用于故障估计，该方法将故障视为系统状态进行增广，然后进行卡尔曼滤波处理。随着系统及偏差维数的增加，增广状态估计法的计算负荷急剧增加，计算速度和估计精度都会下降。基于偏差分离原理的故障估计算法同样源于增广状态估计的设计思路，但能有效避免该状况的发生。偏差分离原理的基本思想是：先分别估计无偏状态和偏差，然后利用两者之间的耦合关系得到最优状态估计结果，也被称为二阶卡尔曼滤波(Two-Stage Kalman Filter, TSKF)算法。文献[1]中给出的偏差分离估计算法是TSKF算法最早的形式。此后，Keller等给出了TSKF标准形式[2-3]，并被广泛引用。

Mendel[4]首次将该方法扩展到非线性系统中，提出二阶扩展卡尔曼滤波(Two-Stage Extended Kalman Filter, TSEKF)算法。针对偏差维数较大的情况，Mendel和Washburn提出多阶卡尔曼滤波(MSKF)算法[5]，并将其推广到了系统动态估计中。Ignagni[6-7]对文献[1]中的公式进行优化完善，给出了TSKF的一般通用形式，但给出的滤波器只能得到次优的估计结果，此后，Ignagni又提出了TSKF最优和次优结果对应的一般形式[8]。

此后，为了得到TSKF的最优解，大量学者进行了深入研究。Alouani等用一个代数约束条件表示偏差噪声和系统噪声的相关性，给出了一种最优的二阶卡尔曼滤波(OTSKF)算法[9]，OTSKF算法在约束条件下等价于扩展状态卡尔曼滤波(EKF)算法[10]。同样为了得到最优的估计结果，通过对TSKF中的无偏状态估计器进行优化。2013年，Keller和Sauter针对随机离散线性系统中包含间歇未知输入的情况，通过最小化状态均方误差矩阵的迹，解耦当前时间的未知输入和状态估计，利用TSKF算法得到间歇未知输入和系统状态的最优估计结果，该算法虽然有一步延迟，但计算量小[11]。Hsieh等基于TSKF算法进行了深入系统的研究，提出了OTSKF算法的2种表示形式[12-13]，并提出了GTSKF[14]、RTSKF[15]、HTSKF等算法。

TSKF算法最早由Friedland[1]提出时，并没有针对故障估计的应用进行描述，但实际系统模型中的偏差可以准确地描述控制系统的执行机构故障和敏感器故障。因此，从理论上看来，可认为该算法一经提出就是适用于线性系统故障估计的算法，即TSKF算法可直接应用于线性系统故障估计。

在应用TSKF算法处理非线性系统故障时，通常的做法是利用EKF的思想，通过计算雅可比矩阵将非线性系统模型进行线性化，然后对线性化后的系统模型应用TSKF算法进行故障估计，这是TSEKF算法的基本思想。在此基础上，很多学者又推导了TSEKF的各种形式，使滤波器具有鲁棒性[16]、自适应性[17]等特性。

近年来，笔者将TSKF、TSEKF算法应用于卫星姿控系统执行机构/敏感器故障估计，经过前期研究发现[18-19]：当姿控系统中飞轮等执行机构、星敏感器等角度测量敏感器出现加性或乘性故障时，基于TSEKF的故障估计算法可以正确估计出故障的幅值；然而光纤陀螺等角速度测量敏感器出现故障时，该算法虽然能在一定程度上估计出故障的幅值，但估计结果中会出现周期性偏差项，且无法通过调整卡尔曼滤波参数得到改善。出现该偏差的原因是：在TSEKF算法中使用EKF的思想对系统进行了线性化处理，导致二次及以上高阶项被忽略，从而引起角度测量故障估计结果的不准确。而UT变换在处理非线性项时，能够保持以至少三阶泰勒精度逼近任何非线性高斯系统状态的后验均值和协方差，因此基于UT变换的无损卡尔曼滤波(UKF)算法的理论估计精度优于EKF算法。

因此，本文针对该问题提出了一种使用UKF思想的二阶无损卡尔曼滤波(Two-Stage Unscented Kalman Filter, TSUKF)算法，用以解决TSEKF中线性化处理造成估计不准确的问题。不同于EKF将非线性模型线性化的技术手段， UKF直接处理非线性模型，目前在处理非线性系统状态估计问题时应用广泛，如导航系统定位[20-21]、航天器姿态确定[22]、电源状态估计[23]等问题。将UKF算法与TSKF算法相结合，能够在将非线性项与线性项分离之后有效地处理非线性模型的估计问题。相较于文献[24-25]中提出的类似TSUKF算法，本文算法完全不需要非线性系统模型的线性化。同时，为解决过程噪声和量测噪声协方差等统计数据不准确导致的滤波器收敛过慢问题，在TSUKF的基础上提出了一种使用量测数据进行自适应的故障估计算法——自适应二阶无损卡尔曼滤波(Adaptive Two-Stage Unscented Kalman Filter, ATSUKF)算法，实现参数的自适应调节。对本文算法进行对比仿真，验证有效性。

1 ATSUKF算法

1.1 基本TSUKF算法

考虑如下非线性离散随机系统：

(1)

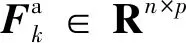
其中：Qx为系统噪声方差阵；Qb为故障噪声方差阵；R为量测噪声方差阵；δk,j为Kronecker符号。

根据UKF算法的一般形式，可知UKF与EKF具有相同的算法结构，只是UKF算法直接使用了系统模型，避免了线性化带来的误差。为解决TSEKF算法对姿态角测量故障无法准确估计的问题，直接将UKF思想引入TSKF滤波器中，得到与TSEKF[19]形式类似的TSUKF算法。

TSUKF算法给出的TSUKF滤波器如下：

(2)

(3)

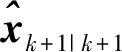
i=0,1,…,2n

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

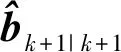
(14)

(15)

(16)

(17)

(18)

式中：Ep为p阶单位矩阵。状态与偏差的耦合关系式为

(19)

(20)

(21)

(22)

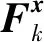
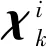
λ=α2(n+κ)-n

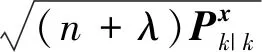
1.2 自适应改进

TSUKF算法能够估计出卫星姿控系统中执行机构和敏感器故障的大小，但统计参数(Qx、Qb和R)的选取对故障估计的精度和速度影响较大，而实际系统中往往存在系统模型的统计参数无法准确已知的情况。针对这一情况，在TSUKF算法的基础上提出ATSUKF算法，在滤波过程中对以上参数进行自适应调整，保障故障估计结果的准确性对仿真参数的变化不敏感。

受Hajiyev和Soken提出的鲁棒自适应卡尔曼滤波器[26]启发，本文对噪声协方差乘以一个多维的自适应因子矩阵，使用测量数据实现对噪声协方差矩阵的自适应，用于系统模型参数未知情况下的卫星姿控系统故障估计。

ATSUKF的系统模型与TSUKF相同，基本滤波器设计也与其相同，通过引入标度矩阵S来实现对量测噪声协方差的自适应。系统量测方差表示为

Sk+1R

(23)

同时，根据实际测量数据可以得到

(24)

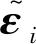
(25)

因此，有

Sk+1R

(26)

进而可以算得

(27)

理想情况下，噪声方差和系统模型匹配，那么标度矩阵即为单位阵。实际上，通过式(27)计算得到的标度矩阵可能并非一个对角阵，并且对角元素可能小于等于0(数学仿真计算时可能出现这种情况，但实物系统不存在)。为了避免数学仿真计算中这种情况的发生，需要对标度矩阵进行处理：

Sk+1=diag(s1,s2，…，sn)

(28)

式中：

si=max{1,Sk+1,ii}i=1，2,…，n

(29)

在对量测噪声方差中的R进行自适应处理后，同样可以对系统噪声方差阵Qx和Qb求取相应的自适应矩阵。

对于Qx的自适应矩阵Λx，对式(26)进行处理可以得到

(30)

式中：

(31)

从而得到自适应矩阵为

(32)

与标度矩阵S一致，Qx的自适应矩阵Λx同样是对角线元素≥1的对角矩阵，因此定义

(33)

式中：

(34)

(35)

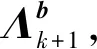
(36)

从而有

(37)

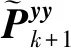
(38)

同样对其进行处理，得到

(39)

式中：

(40)

(41)

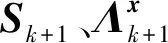
2 快速机动卫星姿态/故障估计

2.1 卫星姿控系统建模

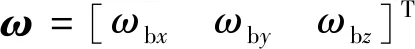
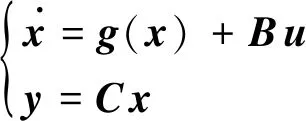
(42)

式中：

C=E6

φ1=Φ(x)

φ2=Φ(x)Abt(x)

Abt(x)=Cy(θbt)Cx(φbt)Cz(ψbt)

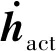
(43)

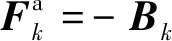
对于卫星姿控系统而言，当卫星处于姿态稳定状态下，通过姿态角的小量化假设可以将系统模型当作线性系统处理，进行常规的姿态滤波估计。另外，卫星姿态稳定时，控制器传输给执行机构的指令力矩近似为0，执行机构的乘性故障不会对系统姿态造成影响。

然而，当卫星处于姿态机动状态时，一方面，系统模型经过线性化处理后往往无法准确描述机动过程中的系统动态特性。另一方面，执行机构接收到的控制力矩指令实时变化，此时必须考虑执行机构的乘性故障对卫星姿态造成的影响。

因此，在接下来的卫星姿控系统故障估计过程中，设置卫星姿态始终处于快速机动状态，在系统具有强非线性的条件下，对比验证TSUKF算法和ATSUKF算法的估计效果。

2.2 仿真分析

对TSUKF算法和ATSUKF算法进行数值仿真对比，仿真条件与所需的初始值如下。

1) 卫星的转动惯量矩阵为

J=diag(17,12,10) kg·m2

跟踪目标姿态角φt为

2) 反作用飞轮最大输出力矩为0.1N·m，最大角动量为2N·m。

3) 系统仿真周期为0.01s，飞轮控制周期为0.1s，滤波采样周期为0.05s。

4) 对于非线性的航天器姿控系统(43)，设计控制律如下：

式中：

KD和KP为控制器参数，在仿真时分别取：KD=0.54E3,KP=0.09E3。

2.2.1执行机构故障

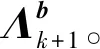
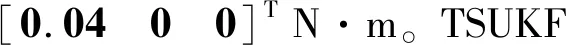
Qb=(2×10-5N·m)2E3

仿真结果如图1所示。由于自适应因子的变化过于剧烈，因此在图中以对数形式指出其数量级的变化。

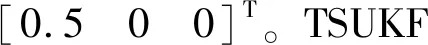
Qb=(2×10-4)2E3

Qx=

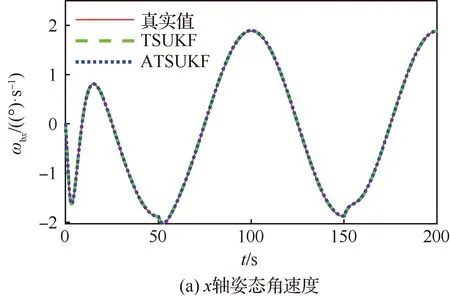
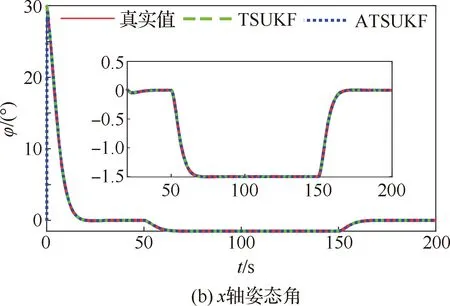
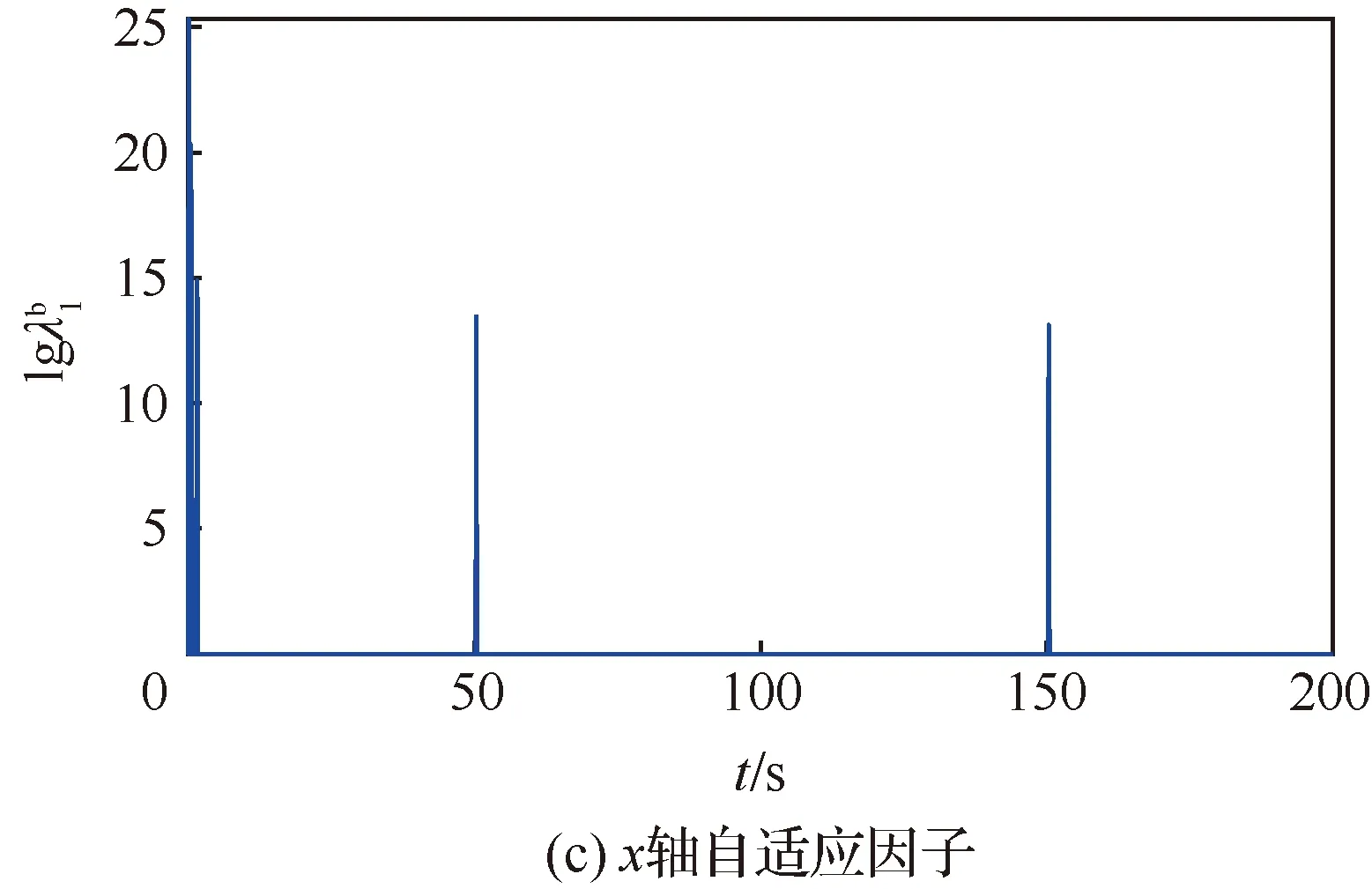
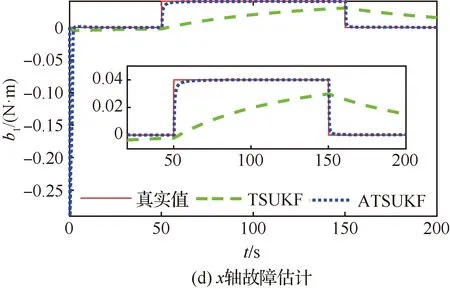
图1 飞轮加性故障下ATSUKF与TSUKF仿真结果Fig.1 Additive faults simulation results of reaction wheels by ATSUKF and TSUKF

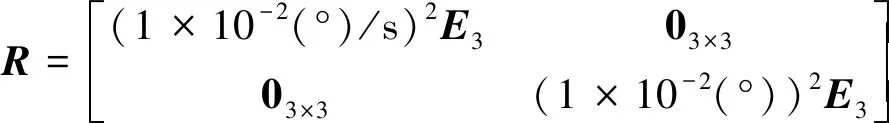
仿真结果如图2所示。

图1(a)、图1(b)和图2(a)、图2(b)分别给出了对于x轴姿态角速度和姿态角的估计结果，可以发现，TSUKF算法和ATSUKF算法对于姿态信息的估计结果区别不大。

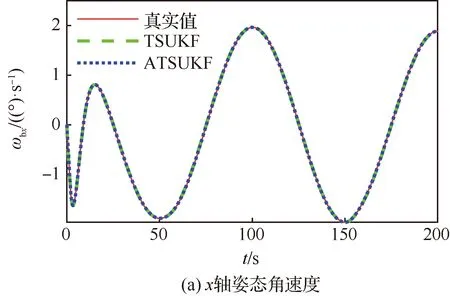
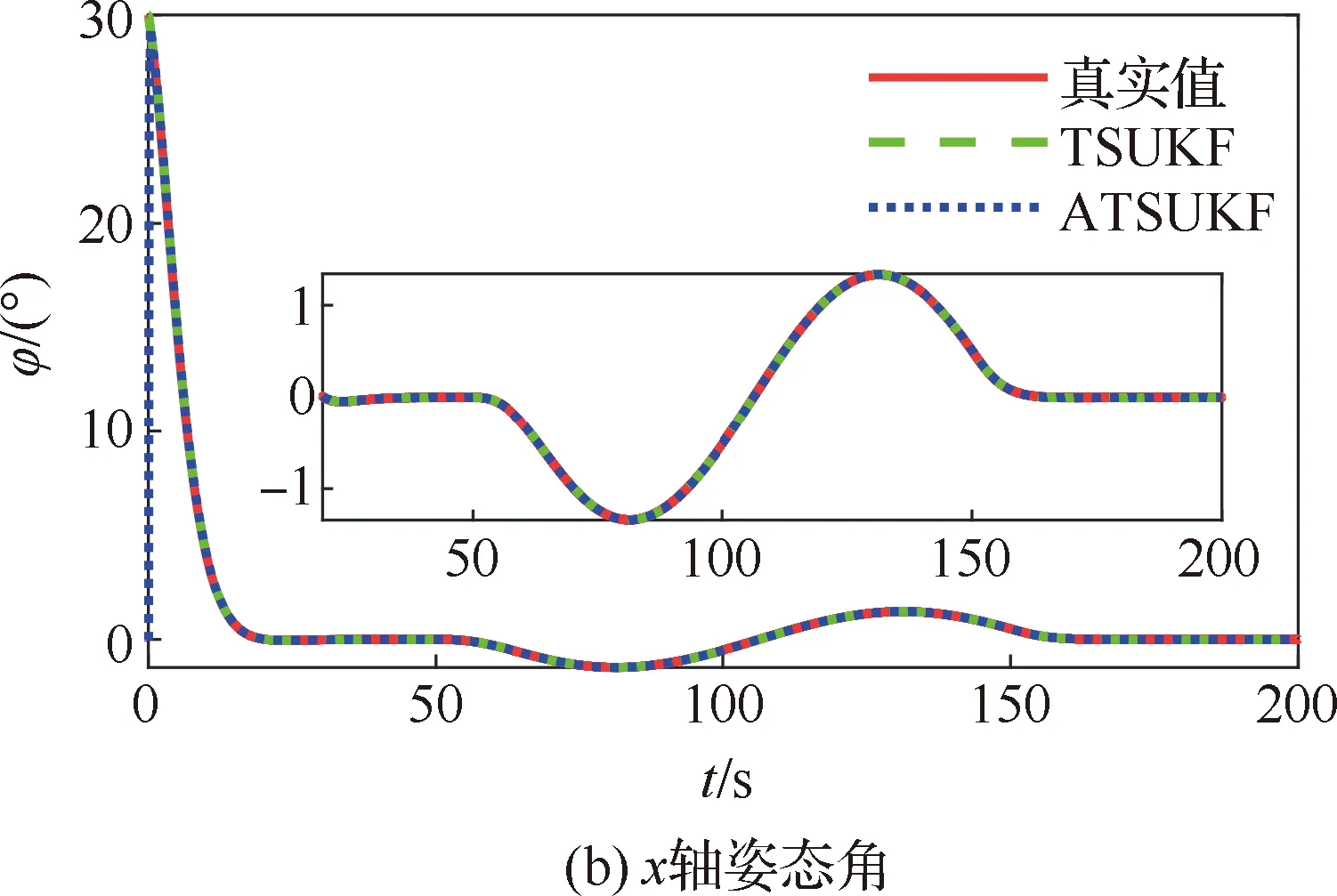
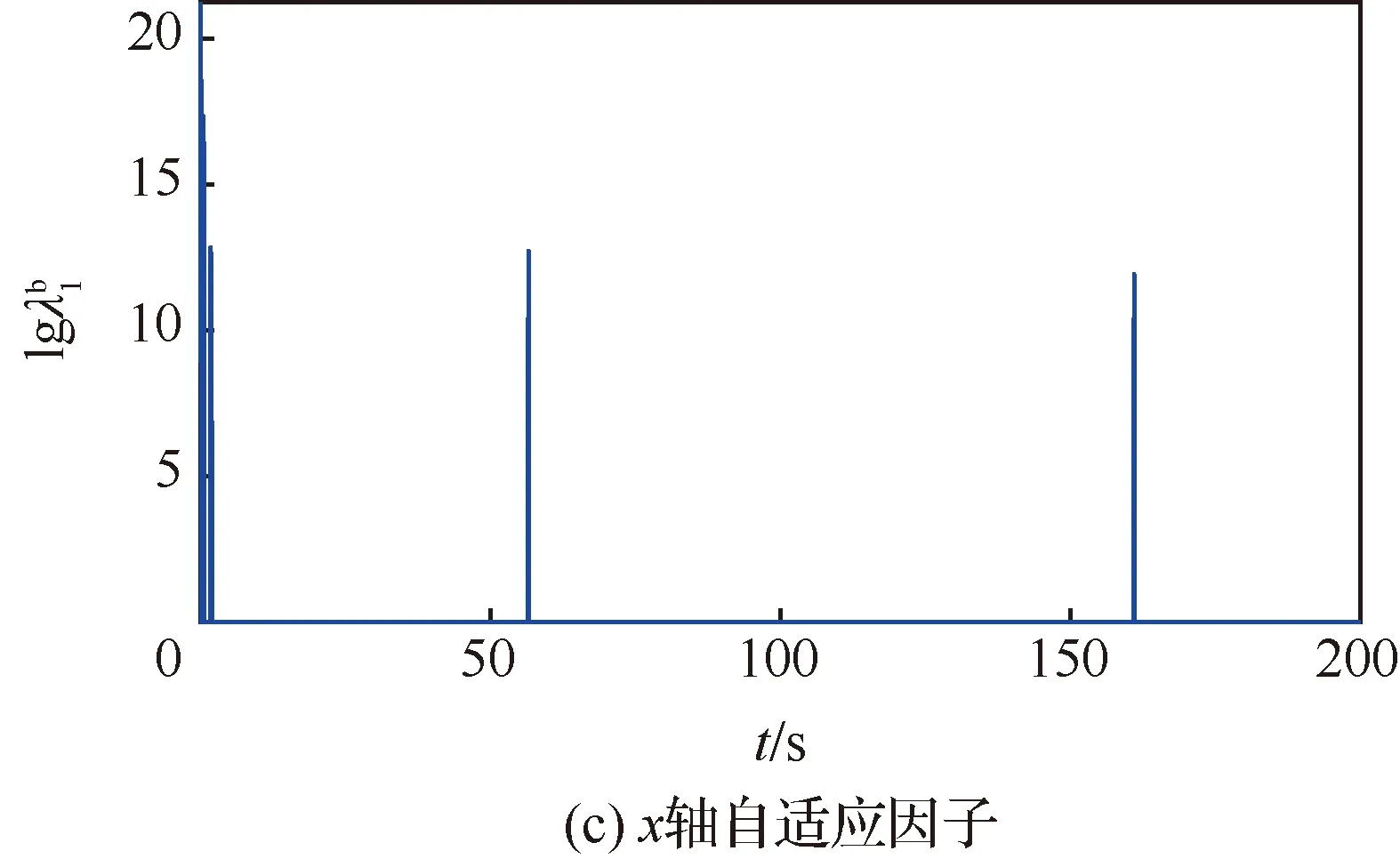
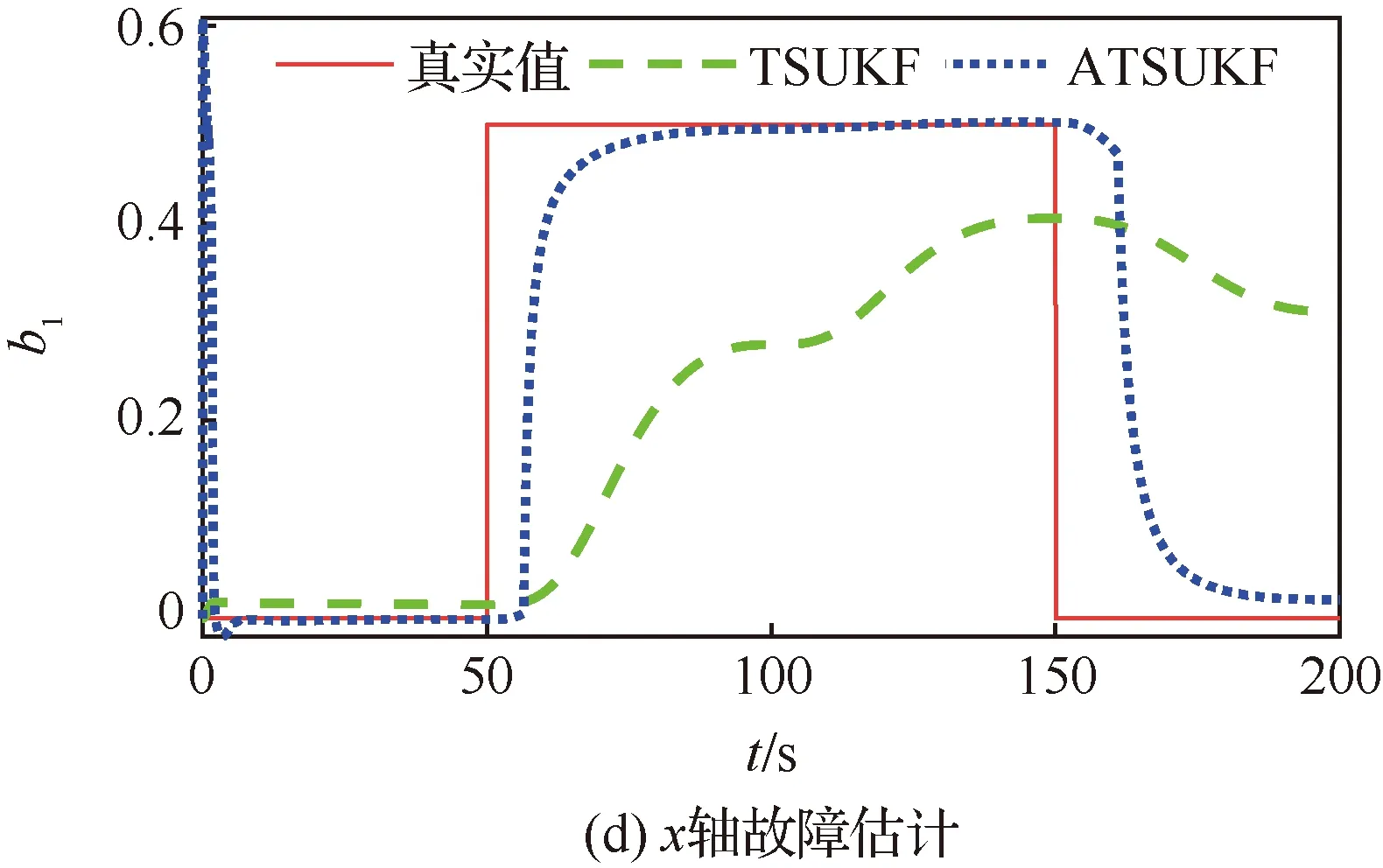
图2 飞轮乘性故障下ATSUKF与TSUKF仿真结果Fig.2 Multiplicative faults simulation results of reaction wheels by ATSUKF and TSUKF

从图1(c)可以看出，第50 s和第150 s时自适应矩阵中对应x轴的对角线元素发生了巨大的变化。故障信号发生变化之后，其数值的数量级从100增加到了1013。第50 s发生故障和第150 s故障消失时，故障发生了变化，量测数据与估计值不再匹配，通过计算可以得到自适应因子突然变大，增大了方差噪声矩阵，从而使算法快速收敛。而在其他区段，由于未发生故障或者故障稳定，自适应矩阵不会发生突变，对角线上的自适应因子均为1。而对于乘性故障，故障发生和消失时控制器发给执行机构的指令力矩幅值极小，此时乘性故障对系统的影响过小，因此从图2(c) 可以发现对于故障发生时间的检测有一定的延迟。从图1(d)和图2(d)可以发现，故障估计结果与自适应因子变化结果可以得出相同的结论，在第50 s和第150 s开始发生变化。

另外，从仿真结果可以看出，自适应矩阵在故障发生变化时自适应因子的突变可以直接用于判断故障是否发生变化。

从图1(d)和图2(d)可以看出，TSUKF算法在卡尔曼滤波参数过小的情况下滤波收敛过慢，无法正常估计出故障幅值。而ATSUKF算法因为自适应矩阵的存在，可以根据量测数据调整噪声方差矩阵的大小，从而实现对故障的快速估计，效果优于TSUKF算法。

2.2.2 敏感器故障

考虑测量姿态角速度的光纤陀螺发生故障，仿真时间200 s，故障设置为50 ～150 s陀螺发生故障，x轴测量存在0.1 (°)/s的常值偏差。TSUKF算法和ATSUKF算法中的噪声方差参数均设置为

Qb=(2×10-7(°)/s)2E3

仿真结果如图3所示。

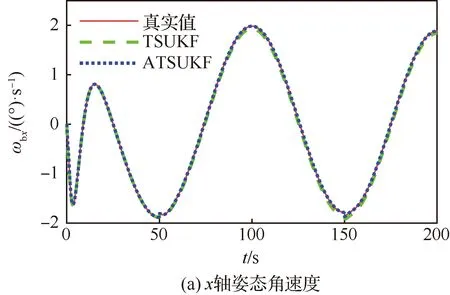
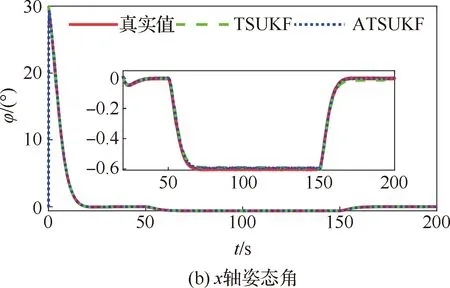
图3 ATSUKF与TSUKF估计陀螺故障结果Fig.3 Faults estimation results of gyros by ATSUKF and TSUKF

从数学仿真结果可以看出，与飞轮故障类似，在系统参数设置不准确的情况下，相比TSUKF算法，ATSUKF算法对姿控系统中光纤陀螺角速度测量故障的估计效果更好，能够更快速地估计出故障的幅值。当故障发生后自适应因子变大，增大方差，加速滤波收敛。从对故障估计的结果可以看出，对于光纤陀螺故障，ATSUKF算法能够很好地进行估计。

综合执行机构和敏感器故障的仿真结果可以看出，在统计特性不准确的情况下，通过引入自适应矩阵，ATSUKF算法对故障的估计效果优于TSUKF，算法收敛更快，对故障的跟踪效果更好。

3 结 论

1) 本文在TSKF中融入UKF思想，首先得到TSUKF算法用于系统故障估计，并在此基础上考虑系统噪声统计信息不确定的情况下结合自适应因子提出了ATSUKF算法。

2) 针对先验信息不足或故障发生变化等系统噪声协方差无法准确已知的情况，ATSUKF算法使用测量数据和残差信息来自适应地调整噪声方差阵，与TSUKF算法相比，ATSUKF算法的估计结果收敛速度更快，避免了传统TSUKF算法需要不断调试滤波器参数的麻烦。