液体火箭发动机推进剂泵诱导轮与离心轮的匹配

杨宝锋，李斌，陈晖，刘占一

1. 西安航天动力研究所 液体火箭发动机技术重点实验室，西安 710100 2. 航天推进技术研究院，西安 710100

作为液体火箭发动机核心部件之一，涡轮泵主要用于推进剂的输送及增压。随着中国大推力补燃循环火箭发动机的研制以及发动机性能提升的迫切需求，涡轮泵的性能以及运行稳定性受到越来越多的重视。

与普通民用离心泵相比，火箭发动机推进剂泵转速较高、结构更为复杂，在叶轮入口处容易发生汽蚀，通常采用加装前置诱导轮来改善泵组的汽蚀性能，然而诱导轮与离心轮匹配不佳将会引起泵性能恶化以及流动不稳定现象的发生，对发动机工作的可靠性产生威胁[1]。近年来，针对离心泵性能及流动不稳定问题，国内外学者已做了大量的研究工作，主要集中在不同工况及结构参数对离心泵性能及压力脉动的影响，获得了丰富的研究成果。郭晓梅等[2]对有无诱导轮以及诱导轮结构变化对离心泵汽蚀性能的影响进行了研究，得到了诱导轮汽蚀严重性与离心叶轮汽蚀严重性并非成正比的结论。王洪杰等[3]对涡轮泵0.75倍额定流量工况下的压力脉动特性进行了研究，指出诱导轮与离心轮间隙为5 mm左右时能改善该工况下的异常振动。Stel等[4]采用数值方法研究了不同流量以及转速对两级离心泵性能的影响，并给出了扬程与转速、流量之间的关系式。Al-Qutub等[5]试验研究了叶轮叶片V型出口对压力脉动的影响，指出采用V型出口叶片后压力脉动降低30%以上，而扬程降低5%；Barrio等[6]利用数值方法研究了叶轮蜗壳间隙大小对离心泵压力脉动以及径向力的影响，表明间隙减小使得压力脉动及径向力显著增加。Zhang等[7-9]采用数值及试验方法对某型低比转速离心泵内不稳定流动与压力脉动关系进行了研究，并对不同叶片尾缘形状对压力脉动影响进行了分析，指出压力脉动幅值与涡量分布密切相关。Long等分别采用数值[10]和试验[11]方法对非均匀入流下核反应堆冷却泵非定常特性进行了研究，表明入口不均匀流动对泵扬程以及压力脉动具有显著影响，在离心泵的设计中应当给予考虑。然而上述研究主要集中在低转速普通离心泵，对高速离心泵尤其是时序效应对其性能及稳定性方面的研究还比较匮乏。

时序效应的研究始于涡轮及压缩机领域，主要研究转子-转子或静子-静子之间周向相对位置变化对涡轮以及压缩机气动性能的影响，获得了较多的研究成果[12-14]。然而时序效应在水力机械领域的研究起步较晚，主要集中在导叶/隔舌时序效应[15-19]以及多级泵级间叶轮时序效应这两方面的研究[20-22]，对离心泵诱导轮与离心轮周向匹配产生的时序效应研究很少见到。徐成波[23]和潘中永[24]等对高速离心泵诱导轮离心轮匹配关系进行了研究，但其针对的是能量匹配以及叶片安装角的汽蚀性能的影响，并未对两者周向相对位置变化引起的时序效应进行研究。卢金玲等[25]对诱导轮离心轮时序效应进行了初步研究，但其研究模型较为简单，且转速较低，对于复杂高速离心泵(如火箭发动机涡轮泵)，其参考价值不高。

本文以中国某型液体火箭发动机涡轮氧泵为研究对象，基于计算流体力学(CFD)全流道数值仿真结果，对诱导轮离心轮匹配的时序效应对泵外特性及压力脉动的影响进行了研究，研究结果可为高速离心泵减振以及性能提升提供指导。

1 计算模型和数值方法

1.1 物理模型

本文研究模型为全尺寸涡轮氧泵，其几何参数如表1所示，转速为18 000 r/min，流体介质为低温液氧，温度为90 K，密度为1 086.9 kg/m3，黏性系数为1.5×10-4Pa·s。为保证仿真结果准确可靠，考虑前后泄漏流域，建立离心泵全流场仿真模型如图1所示，共包含入口域、诱导轮域、叶轮域、扩压器域、蜗壳域和前后泄漏域以及出口管道8个流域。此外，为消除进出口边界扰动的影响，将泵入口及出口管道沿直线延长一段距离。

表1 泵几何参数Table 1 Geometrical parameters of pump

图1 计算域Fig.1 Computational domain

为研究诱导轮离心轮时序效应的影响，定义诱导轮叶片尾缘与离心轮主叶片前缘夹角沿轴向投影为匹配角度θ。考虑到周向匹配的循环对称性，在60°对称周期内，平均选取8个周向位置(θ=0°, 7.5°, 15°, 22.5°, 30°, 37.5°, 45°, 52.5°)研究时序效应对泵外特性的影响，其中0°、 15°、 30°和45°这4个角度用于研究时序效应对非定常压力脉动的影响。

1.2 网格生成与计算设置

利用ICEM软件对各流域进行六面体结构化网格划分，以提高计算精度及收敛性，最终获得的离心泵全流域如图2所示。对各壁面区域进行加密，使得离心轮叶片以及扩压器叶片等关键壁面平均y+<10，其余壁面平均y+<300，以满足计算要求。采用4套网格方案进行网格无关性验证，各流域网格数见表2。额定工况下，各方案下泵效率计算结果如图3所示，可以看出，当网格数超过3 000万时，计算效率基本一致，其中方案2与方案4计算结果误差仅0.25%。为能够更为准确地捕捉流场细节，最终选取方案3网格(网格数为6 655.65万)进行非定常仿真计算。

图2 全流域网格轴向截面图Fig.2 Grid of whole domain in axial cross-section

表2 各流域网格数Table 2 Grid number of each part

流域网格数/106方案1方案2方案3方案4入口0.62810.93131.37822.2114诱导轮2.76146.798011.096116.7832离心轮7.13939.913322.326432.1822扩压器2.10854.79709.533914.2709蜗壳2.81663.426411.128118.3977前泄漏1.72352.25414.22208.9803后泄漏2.44253.16126.571213.3173出口管0.30060.30060.30060.3006总计19.920531.581966.5565106.4436

图3 网格无关性验证Fig.3 Grid independence validation

采用商业软件ANSYS CFX 17.2对三维全流道进行数值计算。对于定常仿真，采用雷诺平均Navier-Stokes(RANS)方法进行求解，湍流模型选取SST (Shear Stress Transport)k-ω模型，壁面处采取Automatic Wall Function进行处理，动静耦合交界面采用Frozen Rotor模型进行数据传递，收敛精度设定为1×10-5。针对复杂模型难收敛现象，首先以一阶格式进行计算，控制物理时间尺度使计算结果收敛；以收敛结果为初值，选取高精度格式继续计算，直至结果收敛。对于非定常仿真，以定常收敛结果作为初始边界，采用DES (Detached Eddy Simulation)方法进行求解，壁面处采用RANS方法求解，以避免实际工程问题中LES (Large Eddy Simulation)方法在壁面处网格量要求过大的限制，主流区域采用LES方法进行求解，以更好地模拟复杂流动，捕捉流场细节，动静耦合面采用Transient Rotor Stator模型进行模拟。为保证非定常仿真结果的可靠性，时间步设置为Δφ= 1°，即每个旋转周期对应360个时间步，计算进行20圈以获得可靠的收敛结果，取最后5圈结果用于非定常结果分析。边界条件根据涡轮泵真实工作状态测量值分别定义为总压入口和质量流量出口，各壁面给定无滑移边界条件。

仿真计算在航天推进技术研究院高性能仿真平台进行，每个算例使用5个节点共80个 CPU核数，非定常仿真每个算例耗时约1 000 h。

1.3 仿真结果验证

仿真结果通过两部分试验进行验证。其中泵外特性仿真结果通过涡轮泵水力试验结果进行对比验证；非定常压力脉动仿真结果与发动机热试车相应测点(图1测点)测量结果(采样频率为25 600 Hz)进行对比验证，其中诱导轮离心轮安装角度接近30°。

涡轮泵水力试验在西安航天动力研究所水力试验中心进行，试验对象为全尺寸涡轮泵，试验介质为常温水，水试转速为9 000 r/min，测量7种不同流量下泵的扬程及效率，并通过相似准则转换到额定转速下与仿真结果进行对比。

仿真与试验获得的氧泵外特性曲线如图4所示(图中Q/Qd为泵内流量与额定工况下的流量之比)。可以看出，整个流量范围内，仿真结果与试验结果吻合较好，总体上仿真结果高于试验结果，在低工况时误差较大，在额定工况附近误差较小，其中额定点扬程、效率误差分别为1.52%和2.73%，表明额定工况点泵外特性仿真结果的可靠性。

图5给出了仿真以及试验中氧泵出口管道测点(OD1)压力脉动时域结果。其中仿真结果为5个周期数据，试验结果为50个周期数据，可以看出两者时域结果吻合较好，压力系数峰-峰值误差<5%。对压力信号进行快速傅里叶(FFT)变换，其频域结果如图6所示(图中f为频率,fr为转子转频)。由图6(a)可以看出，仿真结果中压力脉动由6倍频和12倍频主导，这两个频率由离心轮扩压器之间动静干涉效应引起，其中6倍频为离心轮主叶片的通过频率(fMBPF)，12倍频为离心轮总叶片的通过频率(fBPF)。而热试车由于环境复杂，其所得压力频谱组成也较为复杂，除了动静干涉的主导频率外，还出现了1倍频(fr)、3倍频(3fr)等其他幅值相对较高的频率。其中1倍频是由于真实产品装配误差导致转子偏移轴线从而破坏转子轴对称性导致；3倍频的出现可由本文后续分析解释，是由于诱导轮离心轮匹配引起。总体来说仿真结果能够准确地捕捉动静干涉主导频率及幅值，其中6倍频幅值误差为60.4%，12倍频幅值误差为30.9%，考虑到试车测量环境复杂性，该误差可以接受。证明本文后续研究匹配效应对动静干涉压力脉动的影响具有可靠性。

图4 数值与试验结果对比Fig.4 Comparison between numerical and experimental results

图5 出口管道测点压力脉动时域结果Fig.5 Time-domain pressure pulsation of monitor point at outlet duct

图6 出口管道测点压力频谱Fig.6 Pressure spectrum of monitor point at outlet duct

2 外特性分析

2.1 匹配角度对泵性能的影响

图7给出了额定工况下诱导轮离心轮不同匹配角度下泵扬程系数以及效率的变化曲线。可以看出，周向匹配产生的时序效应对泵扬程及效率具有一定的影响，随着匹配角度的增加，扬程、效率均呈现先降低后缓慢增加的趋势，两者变化幅度分别为0.8%、1.2%。其中0°时具有最高的扬程及效率，30°时达到最低值，这表明当诱导轮叶片尾缘与离心轮叶片前缘相对时，可获得最高的扬程及效率。

图7 不同匹配角度下泵性能变化情况Fig.7 Pump performance variation at different matching angles

2.2 熵产分析

为阐释匹配效应对泵性能的影响，引入熵产理论对泵内部能量损失进行分析。流场熵产分析方法由Kock和Herwig[26]提出，近两年来才逐渐应用到水力机械领域中，取得较好的效果[27-28]。其将湍流流场损失分为湍流平均运动引起的损失以及脉动运动引起的损失两大部分(湍流耗散损失)，两者的计算表达式为

(1)

(2)

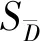
泵内各部件能量损失可通过对式(1)和式(2)进行体积分来获得，即

(3)

式中：V为流体体积。

由熵产理论获得各部件损失随匹配角度变化曲线如图8所示，可以看出，叶轮及扩压器流域损失远大于其他流域损失，随着匹配角度增加，呈现出先增加后减小的趋势，这与外特性曲线变化趋势相对应。其他流域随匹配角度变化损失变化不大，由此可以得出，诱导轮离心轮匹配的时序效应对外特性的影响主要来自离心轮及扩压器流域流动状态的变化。

图9给出了诱导轮、离心轮Blade to Blade (B2B)中截面的局部熵产率(Local Entropy Production Rate, LEPR)以及流线分布图。由图9(a) 可以看出，离心轮内损失远大于诱导轮内损失，当匹配角度θ为0°和15°时，高熵产区域主要分布在靠近诱导轮叶片的3个流道内(图中椭圆标注)，而在匹配角度为30°和45°时，其余3个流道也出现较高熵产分布，因此也导致更高的损失的发生，这与图8的损失变化趋势相符。由图9(b) 流线分布可知，较高的熵产分布区域对应较强的流动分离以及由此产生的分离涡，在匹配角度为0°和15°时，靠近诱导轮的3个叶片通道出现明显的流动分离，其余3个通道流动状态相对较好，而在匹配角度为30°和45°时，6个叶片通道均出现不同程度的流动分离以及相应的分离涡，几乎堵塞了整个流道，最终导致扬程效率的下降。此外，由离心轮内流动状态可知该离心轮具有较大的优化空间。

图8 不同匹配角度下各流域的能量损失Fig.8 Energy loss of each domain at different matching angles

图9 诱导轮、离心轮B2B中截面LEPR及流线分布Fig.9 Distribution of LEPR and streamlines in B2B cross-section of inducer and impeller

图10给出扩压器内熵产率及流线分布图，由图10(a)可知，不同匹配角度下熵产分布模式相似，其中高熵产区域主要分布在扩压器入口处叶轮尾迹区域以及靠近隔舌处的叶片通道内(通道A，虚线椭圆标注)。随着角度变化，高熵产区域也在变化，θ=30°时扩压器入口处以及叶片通道A中高熵产区域显著增大，对应着较大的损失产生。由图10(b)可以看出，在通道A中出现明显的回流现象，匹配角度为0°时，回流现象不明显；在θ=30°时，回流现象显著增强，并发展成较强的回流涡，堵塞了整个通道A，这也是高熵产区域增大，损失增加的一个重要原因；此外，在其他通道也出现流动分离等不稳定现象(图10(b)中实线椭圆标注)，然而此区域能量损失很小，这表明传统的利用流线分析确定流场损失的方法存在一定的缺陷。

通过熵产分析可知，诱导轮离心轮匹配对外特性的影响主要由离心轮及扩压器内流动状态决定，其形成机制为：不同匹配角度下，叶轮通道内分离涡、叶轮尾迹效应以及靠近隔舌的扩压器叶片通道内回流涡的变化共同作用导致。

图10 扩压器B2B中截面LEPR及流线分布Fig.10 Distribution of LEPR and streamlines in B2B cross-section of diffuser

3 压力脉动分析

3.1 压力脉动强度分布

为了对离心泵整个旋转周期内流场的压力脉动强度进行评估，通过引入压力脉动标准差与叶轮出口处动压进行无量纲化，定义相应的压力脉动强度系数Cpsd如式(4)所示，其优势在于能够获得流场内压力脉动强度分布情况，准确定位流场内高压力脉动发生的位置。

Cpsd=

(4)

式中：N为一个计算周期内时间步数，即压力采样数；p(x,y,z,ti)为节点(x,y,z)在第i个时间步的静压大小；U2为叶轮出口圆周速度。

图11为诱导轮流域B2B平面内压力脉动强度分布，可以看出诱导轮内压力脉动水平较低，较高的压力脉动主要分布在叶片出口压力面处；此外，不同匹配角度下压力脉动强度分布相同，表明时序效应对诱导轮内压力脉动影响较小。

图12给出了离心轮、扩压器以及蜗壳中截面压力脉动强度分布情况。与图11相比，这3个流域的压力脉动强度水平远高于诱导轮流域。此外，高压力脉动区域主要集中在动静干涉区域以及扩压器导叶入口吸力面附近。由图12可知，不同匹配角度对压力脉动强度分布影响显著，当匹配角度为0°时，压力脉动水平最高，各导叶入口处高压力脉动区域大小相当；随着匹配角度变化，压力脉动水平开始下降，尤其表现在扩压器导叶入口处。当匹配角度为30°时，即诱导轮叶片尾缘位于离心轮相邻主叶片中间位置时，压力脉动水平达到最低状态，主要表现为扩压器导叶入口处高压力脉动区域以及蜗壳区域压力脉动的显著减小，并且越远离隔舌的导叶入口处高压力脉动区域减小幅度越大。

图11 诱导轮B2B中截面压力脉动强度分布Fig.11 Distribution of pressure pulsation intensity in B2B surface of inducer

图12 离心轮、扩压器、蜗壳中截面压力脉动强度分布Fig.12 Distribution of pressure pulsation intensity in impeller, diffuser and volute domain at mid-span section

3.2 压力脉动频谱分析

根据压力脉动强度分析结果，对压力脉动水平较高的动静干涉区域以及扩压器导叶附近压力脉动频谱进行分析。图13给出了相应的压力脉动测点分布，在动静干涉区域沿周向平均布置10个 测点，各测点位于导叶叶片前缘附近；在靠近隔舌处的导叶布置4个测点，分别位于导叶前缘吸力面处(DF1)、导叶吸力面(DF2)与压力面(DF4)中部以及导叶尾缘吸力面(DF3)处。此外，在出口管道处设置测点如图1(b)所示，该测点与热试车测点保持一致，用于数值结果与试验结果的对比。

对各测点压力信号进行FFT变换，为了评估压力脉动能量在特定频域变化趋势，定义不同频率离散幅值的RMS值[8]为

(5)

式中：Ai为不同频率下压力脉动幅值。

表3给出了匹配角度为0°和30°时动静干涉区域各测点在0～20 760 Hz频域内压力脉动RMS值(无量纲结果)。可以看出，靠近隔舌的测点RS1压力脉动水平最高，远离隔舌的测点压力脉动水平显著下降，这与3.1节压力脉动强度分析结果相符。当匹配角度为30°时，动静干涉区域压力脉动水平显著降低，各测点RMS幅值均下降10%以上，平均下降14.50%。其中测点RS10降幅最大，达到18.87%。

表4给出了扩压器表面测点在0～20 760 Hz下的压力脉动RMS值(无量纲结果)。可以看出压力脉动最大水平出现在DF1测点，这与3.1节压力脉动强度分析结果高脉动区域分布在导叶入口吸力面附近相符。当匹配角度为30°时，压力脉动水平显著降低，RMS幅值平均下降16.7%。其中测点DF2降幅最大，达到34.76%。

图13 压力脉动测点设置Fig.13 Arrangement of pressure pulsation monitor points

表3 动静干涉区域压力脉动RMS值Table 3 RMS values of pressure pulsation in rotor-stator interaction region

表4 扩压器叶片表面压力脉动RMS值

Table 4 RMS values of pressure pulsation on diffuser blade surface

匹配角度/(°)压力脉动RMS值DF1DF2DF3DF405.28581.27873.30062.4459304.86610.83422.86022.1784Difference/%7.9434.7613.3410.94

根据RMS值分析结果，选取脉动水平最大以及降幅最大的测点(动静干涉区域RS1、RS10；扩压器表面DF1、DF2)进行频谱分析。

图14给出了4种不同匹配角度下测点RS1压力脉动频谱。可以看出，由于动静干涉效应，4种 匹配角度下离心轮叶片通过频率(fMBPF、fBPF)及其倍频起主导作用。此外，由于诱导轮3个 叶片的影响，在0°时，3倍转频(3fr)非常突出，其幅值与主叶片通过频率幅值相当；随着匹配角度变化，3倍频逐渐较小，在30°时，3倍频基本消失，而其他频率幅值基本保持不变。

图15为RS10测点在不同匹配角度下的压力脉动频谱。可以看出，各匹配角度下，叶片通过频率及其倍频起主导作用，当匹配角度为0°时，3倍频较大，其幅值已超过叶片通过频率幅值，随着匹配角度变化，3倍频逐渐减小，并在30°时消失，这与RS1测点变化规律一致。

图14 不同匹配角度下RS1测点压力脉动频谱Fig.14 Pressure pulsation spectra of RS1 at different matching angles

图15 不同匹配角度下RS10测点压力脉动频谱Fig.15 Pressure pulsation spectra of RS10 at different matching angles

图16给出扩压器叶片前缘吸力面附近DF1测点压力脉动频谱。该测点靠近动静干涉区域，因此其频谱呈现出与前述RS1、RS10相似的频谱特性。但由于其位于较高压力脉动区域(如图12所示)，因此各主导频率幅值显著高于RS1、RS10测点。

图17给出了扩压器吸力面中心DF2测点压力脉动频谱。该测点在不同角度下主导频率为主叶片通过频率(fMBPF)，其谐频成分逐渐消失。同样当匹配角度为0°时，3倍频成分也起到主导作用，30°时，3倍频成分消失。由此可以得出结论，诱导轮离心轮周向匹配参数对离心泵动静干涉效应影响显著，当诱导轮出口叶片位于离心轮相邻主叶片中间位置时，能够显著降低压力脉动水平，其本质为降低了压力脉动的3倍频成分。

为对诱导轮与离心轮周向匹配引起的压力脉动3倍转频成分的出现与抑制现象进行解释，图18(a)和图18(b)给出了周向匹配角度为0°以及30°时离心轮内部流线分布情况。由图18(a)可以看出，当匹配角度为0°时，靠近诱导轮叶片出口吸力面的3个流道出现了严重的流动分离(图中椭圆标注部分)，几乎堵塞了整个叶片通道，而其余3个叶片通道流动状态相对较好，整个离心轮流域被平均分成3股循环对称流动。因此在离心轮出口与扩压器入口区域的动静干涉过程中，这3股对称流动引起了较高的3倍转频成分。而当诱导轮叶片尾缘位于离心轮相邻主叶片中间位置，即匹配角度为30°时，这种对称效应被破坏，离心轮6个主叶片通道出现了不同程度的分离现象，因此在随后的动静干涉过程中，3倍频消失，离心轮叶片通过频率(6倍频)及其倍频起到主导作用。

图16 不同匹配角度下DF1测点压力脉动频谱Fig.16 Pressure pulsation spectra of DF1 at different matching angles

图17 不同匹配角度下DF2测点压力脉动频谱Fig.17 Pressure pulsation spectra of DF2 at different matching angles

图18 叶轮流域瞬时流线分布Fig.18 Distribution of instantaneous streamlines in impeller

4 结 论

本文采用基于DES的离心泵三维CFD全流道数值仿真方法对中国某型液体火箭发动机涡轮泵诱导轮离心轮周向匹配产生的时序效应进行了研究，得到以下结论：

1) 诱导轮离心轮周向匹配的时序效应对泵外特性有一定的影响。随着匹配角度的增加，泵扬程及效率均呈现先减小后缓慢增大的趋势，两者变化分别达到0.8%和1.2%。当诱导轮叶片后缘与离心轮叶片前缘正对时，可获得最大的扬程及效率。

2) 通过熵产分析可知，诱导轮离心轮时序效应对能量损失的影响主要集中在叶轮以及扩压器流域。时序效应对外特性的影响机制由叶轮通道分离涡、叶轮叶片尾迹以及靠近隔舌处扩压器叶片通道回流涡的变化所决定。

3) 诱导轮离心轮时序效应对叶轮扩压器动静干涉效应影响显著。当诱导轮叶片后缘位于离心轮相邻主叶片中间位置时，可有效消除3倍频成分，显著降低泵内压力脉动水平。其中动静干涉区域以及隔舌处扩压器叶片表面压力脉动幅值平均下降14.5%和16.7%。