带有临界指数和奇性的椭圆方程正解的存在性
林美琳
(莆田学院数学与金融学院, 应用数学福建省高校重点实验室, 福建 莆田 351100)
0 引言
考虑一类带权的椭圆方程多重正解的存在性问题:
(1)

那么,u∈Ha是方程(1)的一个弱解.
由Sobolev嵌入定理和Hardy不等式, 方程(1)实际上是可变的. 寻找方程(1)的弱解等价于寻找下列函数的临界点.
很多学者对方程(1)这类方程做了大量的研究, 特别是当a=b=0的情况. 文献[1]证明了在0 定理1假设0<λ<Λ且0 以上问题主要采用变分方法来进行研究. 鉴于文献[1-3]的工作, 主要面对的问题如下: 1) 函数I不满足(PS)条件; 2) 方程的解不属于L∞(Ω); 3) 由于非线性u-q的奇性, 函数I是不可微的, 这些需要文献[2-5]的一些思想和方法来解决. 接下来, 看一个极小问题 可以知道S(a,b,μ)的一组达到函数为 易得: 命题1假设0≤λ<Λ, 那么对方程(1)的任意正解u∈C2(Ω{0}), 都存在着正的常数M1,M2, 有 对任意x∈Br(0){0},r充分小都成立. 接下来, 将这个问题的Nehari流形进行分割, 然后在适当的子集上考虑极小问题. 定义 同时定义极小问题 (2) (3) 且令 μ*=min{μ3,μ4} 引理1设u是方程(1)的一个正解, 则对ε>0充分小, 有 此引理的证明见文献[7]. 此引理的证明见文献[7]. 引理3对每一个0≤φ∈Ha, 有 1) 存在ρ0>0, 使得I(ω+ρφ)≥I(ω), 0≤ρ<ρ0. 引理的证明见文献[2]中引理3. 引理4对每一个0≤φ∈Ha, 有ω-qφ,v-qφ∈L1(Ω), 且 (4) (5) 特别地,ω,v>0几乎处处在Ω{0}中. 证明 接下来只证明式(4), 而式(5)可以类似得证. 令φ≥0且ε>0, 由引理3的方程(1)和简单的计算, 有 由于对每一x∈Ω{0}, 当ε→0时, 不等式的右边都趋于有限值, 可以得到当ε→0时,ε-1((ω+εφ)1-q-ω1-q)是单调增加的且 由单调收敛定理知ω-qφ∈L1(Ω), 从而得到式(4). 引理5在定理1的假设条件下: 证明 首先, 从文献[2]知道, 存在t*>0, 使得ω+t*vε∈M-. 剩下的就是证明 由于ω是方程(1)的解, 可以通过直接计算得到: 从文献[2], 有下面的不等式: 另外还有一个不等式: 由以上的不等式可以得到 当t→0或t→∞时,I(ω+tvε)→0. 因此, 对于上面不等式右边的式子, 只考虑t∈[t0,t1]的情况, 其中0 由引理1可以得到 这一部分将证明定理1. 定理1的证明关键是解决极小问题(2)和极小问题(3). 定理1的证明需要分成两步来完成. 第一步将证明, 若存在ω∈M+使得d+=I(ω), 且存在v∈M-使得d-=I(v), 那么ω和v是方程(1)的两个正的弱解; 第二步将证明极小值d+和d-分别是可达的. 第一步: 令ω∈M+使得d+=I(ω);v∈M-使得d-=I(v). 命题2ω和v是方程(1)的两个正的弱解. 证明 对任意φ∈Ha,ρ>0, 定义ψ=(ω+ρφ),ψ+=max{ψ, 0}, 则ψ+∈Ha. 由于ω∈M, 从式(4)可以得到 由φ的任意性知ω是方程(1)的解. 类似可以证明v也是方程(1)的解. 第二步: 极小值d+和d-是可达的. 下面只证明存在v∈M-, 使得d-是可达的.d+可类似得证. 在这里指出vε和ω(命题1)的局部精确估计起到必要的作用. 从命题1还可以知道存在m>0使得对x∈suppω{0}, 有ω(x)≥m. 命题3极小值d-是可达的. 存在v∈M-, 使得I(v)=d-. 证明 令{vn}n∈N⊂M-, 使得I(vn)→d-.易得{vn}在Ha中是有界的. 假设弱vn→v在Ha中, 令zn=vn-v, 假设 由于vn∈M, 由Brezis-Lieb引理和Sobolev嵌入定理, 得到 这和引理5矛盾. 从假设μ∈(0,μ*), 有0 现在, 考虑下面的情况: ①t-<1. ②t-≥1且f>0. ③t-≥1且f=0. 1) 从t-<1,g′(1)=0,g′(t-)>0, 可以得到g在[t-, 1]上是递增的.从而有 由μ∈(0,μ*), 得到g(1)≥g(T0). 若T0≤1, 有 同样和引理5矛盾. 那么由命题2~3就可以直接证明定理1.

1 预备知识


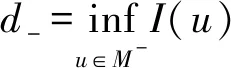

2 几个引理
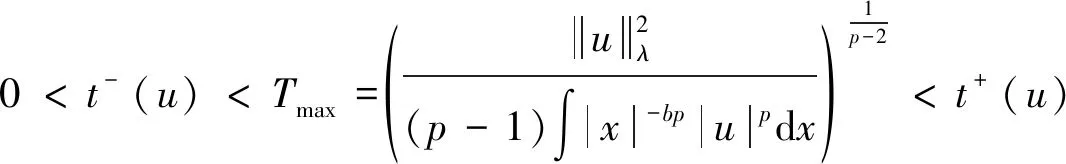




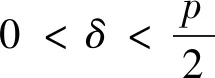
3 定理1的证明









