局部T-凸空间中的不动点定理
陈治友
(贵阳学院数学与信息科学学院, 贵州 贵阳 550005)
0 引言
文献[1]用可缩性代替凸性定义了具有H-凸结构的H-空间, 该空间将先前的线性凸结构进行了推广. 文献[2]指出任何Hausdoff拓扑线性空间、 凸空间、 可缩空间、 伪凸空间都是H-空间. 文献[3]对可缩性与H-凸性的性质进行了深入的研究. 相关学者又研究了一般拓扑空间中的凸结构, 如: 半格凸、 G-凸、 B-凸、 Van de Vel凸、 Michael-凸、 L-凸、 超凸等等. 文献[4-5]发现上述一系列凸结构有一个共性特征, 即都满足H0-条件. 借助文献[1-6]的思想, 文献[7]利用连续映射的延拓性质构造了具有T-凸结构的T-凸空间, 该空间的T-凸性是H-空间的H-凸性的推广, 并且还证明了T-凸空间满足H0-条件. 文献[8-12]在不具有线性结构的广义凸空间中对非线性分析中的一些问题进行了研究. 本研究将在这些工作的基础上, 借鉴文献[13]的思想, 首先引入局部T-凸空间的概念, 然后在局部T-凸空间框架下, 不依赖KKM技巧, 建立了两个新的连续映像的不动点定理, 并且这两个定理分别以局部H-凸空间中的Schauder不动点定理和Browder不动点定理为其特例, 从而将Schauder不动点定理和Browder不动点定理推广到不具线性结构的T-凸空间.
1 预备知识
定义1[7]设X,Y为拓扑空间,A⊂X为X的任意子集,f:A→Y连续, 若存在连续映射f*:X→Y, 使得f*(x)=f(x), ∀x∈A, 则称f可以从A延拓(或扩张)到X.
定义2[7]设X,Y为拓扑空间, 若对X的任意子集A⊂X及任意连续映射f:A→Y,f可以从A延拓到X, 则称A关于X具有延拓性质.
定义3[7]设X为拓扑空间, {TA}为X中给定的一族非空的且关于X具有延拓性质的子集, 以X中一切有限子集A编号, 且当A⊂B时,TA⊂TB, 则称二元对(X, {TA})为T-空间. 集D⊂X称为T-凸的, 如果对任意有限集A⊂D, 都有TA⊂D.
设(X, {TA})是T-凸空间, 定义A⊂X的T-凸包为:coTA=∩{D⊂X:A⊂D且D是T-凸集}.
易验证, 若A⊂X为T-凸当且仅当coTA=A, 记T={A⊂X:coTA=A}.
注1由于拓扑空间中的可缩子集族一定是具有延拓性质的子集族, 而反之不然. 因此H-凸空间是T-凸空间, 而T-凸空间未必是H-凸空间; H-凸集是T-凸集, 而T-凸集未必是H-凸集.
定义4设(X, {TA})是T-凸空间, 若B⊂X,C⊂X, 且对任意有限集A⊂C, 都有TA⊂B, 则称集B关于集C是T-凸的. 特别地, 当C=B时, 据定义3知,B是T-凸的.
定义5设(X, {TA})是T-凸空间, ∀x∈X, 若对x的任一个开邻域U(x), 存在x的另一个开邻域U1(x), 使得U(x)关于U1(x)是T-凸的, 则称T-凸空间(X, {TA})是一局部T-凸空间.
注2由注1知, 局部H-凸空间是局部T-凸空间, 反之不然.
定义6设(X,d, {TA})为T-凸度量空间, 称X的一非空子集B为T-凸度量空间(X,d, {TA})的一致局部T-凸子集, 若∀ε>0, ∃δ>0, 使∀x∈X, 有Uε(x)关于Uδ(x)为T-凸的. 特别地, 当X=B时, 就称X为一致局部T-凸空间, 其中Ur(x)={y∈X:d(x,y) 引理1[7]T-凸空间(X, {TA})满足H0-条件. 即T-凸空间(X, {TA})的T-凸结构{TA}有下面性质: 对每个有限集{x1, …,xn}⊂X, 存在连续映射:f:Δn-1→coT{x1, …,xn}. 使得:f(ΔJ)⊂coT{xj:j∈J}(∀φ≠J⊂N). 其中:Δn-1=e1, …,en是n-1维标准单纯形,e1, …,en是Rn中的标准正交基. 定理1设(Y,d, {TA})为一局部T-凸度量空间,X为(Y,d, {TA})的非空紧T-凸的子集,F:X→X为一连续映像, 则F必有不动点. 显然g:X→Δn-1连续. 另据引理1知T-凸空间满足H0-条件. 因此, 对有限集{F(xi):i=1, 2, …,n}⊂X, 存在连续映像:f:Δn-1→coT{F(xi):i=1, 2, …,n}⊂X, 使得:f(ΔJ)⊂coT{F(xj):j∈J} (∀φ≠J⊂N). 其中:Δn-1=e1, …,en是n-1维标准单纯形,e1, …,en是Rn中的标准正交基. 显然复合映像g∘f:Δn-1→Δn-1为一连续映像, 因此据Brouwer不动点定理, 存在e∈Δn-1, 有g∘f(e)=e. 设f(e)=xe, 故xe∈X, 且xe是f∘g的不动点. 另外, ∀x∈X, 设I(x)={i∈{1, 2, …,n}:βi(x)>0}, 因此有 由于i∈I(x), 因此βi(x)>0, 则x∈Uδxi(xi), 然后据Uδx(x)的取法可知:F(Uδxi(xi))⊂Uη(F(xi)). 所以 F(x)∈F(Uδxi(xi))⊂Uη(F(xi)) (∀i∈I(x)) 再由F(x)∈Uη(F(xi)), ∀i∈I(x)得F(xi)∈Uη(F(x)), 又因Uε(F(x))关于Uη(F(x))为T-凸的, 于是有 f(g(x))∈coT{F(xi):i∈I(x)}⊂Uε(F(x)) 定理1证毕. 由注1~2, 再据定理1, 立即得: 推论1设(X,d)是一度量空间, (X, {ΓA})为一局部H-凸空间,D为(X, {ΓA})中的非空紧子集, 且D为H-凸的. 设P:D→D连续, 则P在D中有不动点. 注3据文献[13]知, 推论1就是著名的Schauder不动点定理在局部H-凸空间中的推广形式, 而定理1是推论1在局部T-凸空间中的推广形式, 因此, 定理1是Schauder不动点定理在局部T-凸空间中的推广形式. 定理2设(Y, {TA})是T-凸空间,X⊂Y为非空紧T-凸子集,F:X→2X为集值映射. 如果∀x∈X,F(x)为非空T-凸的且F-1(x)是开的, 则F必有不动点. 对于X的有限开覆盖{F-1(yi):i=1, 2, …,n}, 一定存在对应的连续单形分解{βi(x):i=1, 2, …,n}:X→[0, 1]. 现构造映像如下: 显然g:X→Δn-1连续. 另据引理1知T凸空间满足H0-条件, 因此, 对有限集{yi:i=1, 2, …,n}⊂X, 存在连续映像 f:Δn-1→coT{yi:i=1, 2, …,n}⊂X 使得 f(ΔJ)⊂coT{yj:j∈J}⊂X(∀φ≠J⊂N) 其中:Δn-1=e1, …,en是n-1维标准单纯形,e1, …,en是Rn中的标准正交基. 显然复合映像g∘f:Δn-1→Δn-1为一连续映像, 因此据Brouwer不动点定理, 存在e∈Δn-1, 有g∘f(e)=e. 设f(e)=x0, 故x0∈X, 且x0是f∘g:X→X的不动点. 最后, 只需证f∘g:X→X是集值映射F:X→2X的一个连续选择即可. 事实上, 对∀x∈X, 设I(x)={i∈{1, 2, …,n}:βi(x)>0}, 则有 于是对每一个i∈I(x), 由βi(x)>0知,x∈F-1(yi), 即yi∈F(x), ∀i∈I(x). 又因为F(x)是T-凸的, 故coT{yi:i∈I(x)}⊂F(x). 因此有∀x∈X,f∘g(x)∈F(x). 定理2证毕. 由注1, 据定理2, 立即得: 推论2设(X, {ΓA})是一H-凸空间,D为(X, {ΓA})中的非空紧子集, 且D为H-凸的,T:D→2D为一集值映像, 若对每一个x∈D,T(x)为非空H-凸的且T-1(x)是开的, 则存在x0∈D, 使得x0∈Tx0. 注4据文献[13]知, 推论2就是Browder不动点定理在H-凸空间中的推广形式, 而定理2是推论2在T-凸空间中的推广形式, 因此, 定理2是Browder不动点定理在T-凸空间中的推广形式. 定理1~2分别是Schauder不动点定理和Browder不动点定理在T-凸空间中的推广. 感谢贵阳学院数学建模及其应用研究中心为本研究提供的基金支持!2 主要结果



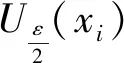






3 结论

