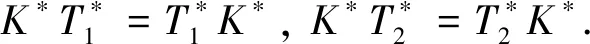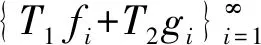Hilbert空间中两个K-框架的算子组合

贾 曼, 朱玉灿

(福州大学数学与计算机科学学院, 福建 福州 350108)

0 引言

1952年, Duffin等[1]在研究非调和Fourier级数问题时正式引入Hilbert空间中的框架概念, 从此国内外众多学者开始对框架理论及其应用进行深入的研究, 并取得了一系列成果. 框架理论的研究成果请参见文献[2-3], 框架也被应用于许多领域, 比如: 信号和图像诊断[4], 采样理论[5]等领域.

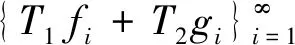
1 预备知识

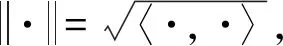
I是H中的恒等算子.B(H1,H2)表示H1到H2的所有有界线性算子的集合, 取H1=H2=H,B(H1,H2)记为B(H), 令K∈B(H)且K≠0, 用R(K)和NK分别表示算子K的值域和核.

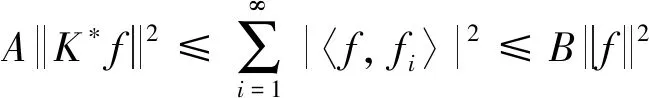
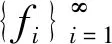
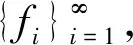
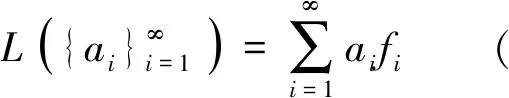
称L为合成算子， 其伴随算子L*:H→l2如下：

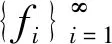
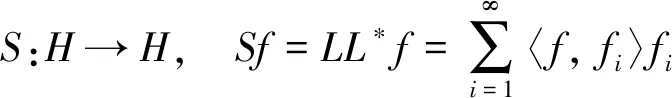
注1特别地, 当K=I时,K-框架就是一般的框架.

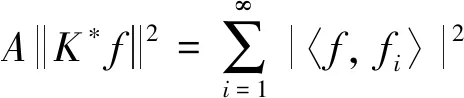
引理1[15]设H1,H2是两个复Hilbert空间,T1∈B(H1,H),T2∈B(H2,H), 则下列叙述等价：

1)R(T1)⊆R(T2).

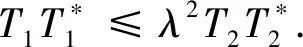
3) 存在X∈B(H1,H2), 使得T1=T2X.

2 主要内容及结论

首先, 给出K-框架和的等价刻画, 该推论修正了文献[9]中命题3.1.

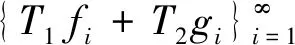
II)R(K)⊂R(T1L1+T2L2).

III) 存在α>0, 使得T1L1(T1L1)*+T2L2(T2L2)*+T1L1(T2L2)*+T2L2(T1L1)*≥αKK*.

同理, 存在正数D, 使得对∀f∈H1

由闵可夫斯基不等式可知, 对∀g∈H2有

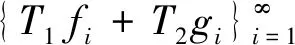
由引理2可知, I)⟺II).

由引理3可知, I)⟺III).

注2在定理1中取H1=H2=H,K=I, 得到推论1, 其修正了文献[9]中的命题3.1(引言中已给出说明).

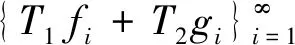
II)T1L1+T2L2为满的.

III)T1L1(T1L1)*+T2L2(T2L2)*+T1L1(T2L2)*+T2L2(T1L1)*>0.

下面给出K-框架和的充分条件.

证明 因为R(K)⊂R(T1L1)且R(K)⊂R(T2L2), 由引理1可知, 存在λ1，λ2>0使得对任意f∈H, 有

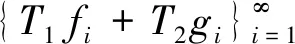
注3在定理2中取T1,T2=I, 得到推论2, 其条件相对于文献[12]中定理4.1的条件更一般了. 在定理2中取T1,T2=I,K=I, 得到推论3, 其推广了文献[9]中定理3.2 (引言中已给出说明).

下面给出紧K-框架和的充分条件.