非正态分布面板数据客观赋权方法对比——基于保险企业社会责任动态综合评价

唐 勇，殷姝婷

（石河子大学 经济管理学院，新疆 石河子 832003）

一、引 言

在多指标综合评价问题的求解过程中，指标的权重举足轻重，被用来反映各指标的相对重要性，如何科学、合理地为指标赋权，关系到多指标评价结果的可靠性与正确性。现有的赋权方法种类繁多，除定性评价外大体可以分为两类，即主观赋权法和客观赋权法。主观赋权法是根据决策者(专家)的主观判断来确定指标权重，包括层次分析法（AHP）、专家打分法（Delph 法）、模糊综合评价法等，其评价结果的主观性较强，在应用中有很大局限性。

客观赋权法主要根据原始数据之间的数量关系来确定权重，其评价结果具有较强的数学理论依据，常用的客观赋权法主要有主成份分析法、熵值法、Topsis 法和投影寻踪模型等，其中主成份分析法、因子分析法等多种赋权方法皆要求数据服从正态分布，其适用性受到影响。以熵值法、Topsis法为代表的线性赋权方法的研究已较为成熟，在各领域应用较广，而以投影寻踪模型为代表的非线性赋权方法的起步相对较晚，起初大量应用于工程学科领域，近几年在经济类领域也得到了广泛的应用。那么多指标、多年份的非正态面板数据如何得到其动态综合评价值，线性赋权方法和非线性赋权方法以及各线性赋权方法间得出的结果是否存在差异，其排名结果是否存在一致性，各赋权方法得出的实证结果是否具有稳定性？都是需要研究和解决的问题。

保险企业通过将风险集中再分散，在灾难降临时给予客户经济上的补偿，从而减轻创伤等机制服务社会，起到了维护社会稳定的作用，同时作为国家医疗保险、养老保险的重要补充，其地位和功能决定了保险企业需要承担更多的社会责任。因此，在根据我国保险企业的特点，参考企业社会责任评价体系的基础上，以我国保险企业社会责任水平为样本进行本文的实证研究，具有重要的现实意义。

二、文献综述

目前国内外学者对投影寻踪综合评价模型、Topsis 模型、熵值法的原理，以及它们在面板数据综合动态评价上的应用都有了大量的研究，对不同赋权方法，部分学者也对其进行了比较，为本文的研究提供了极大的参考和借鉴。

作为本文选取的非线性赋权方法的代表，投影寻踪等级评价模型最早由Kruskal[1]42-48在1972 年提出，他将高维数据投影到低维空间，发现了数据的聚类结构，并用其解决化石分类问题，随后我国学者也对投影寻踪等级评价模型的原理开始研究，陆续证明了其收敛性、极限分布和稳定性，发现该模式十分适用于非正态、非线性高维数据的综合评价（成平，1986）[2]8-12。起初的投影寻踪模型多用于评价环境问题（杨万平，2018）[3]58-67等理工科领域，近年来，其在企业可持续发展能力（苏屹，2018）[4]130-139等经济类领域也得到了广泛的应用，而周一凡（2016）[5]76-83以1994 年至2013 年全国30个省、市、自治区的数据为样本建立电力发展水平动态综合评价模型，为使用投影寻踪模型进行多指标、多年份的面板数据动态综合评价问题提供了思路。

本文选取的线性赋权方法包括Topsis 模型和熵值法模型，其中Topsis 模型是C.L.Hwang 和K.Yoon[6]85-93于1981 年首次提出，对其研究至今已经较为成熟，并于公共服务（朱梅新，2013）[7]110-114、工程（陈为公，2018）[8]7-14等多领域得到广泛应用，并已经在企业社会责任研究领域得到应用（刘梦瑶，2015）[9]116-121，而石宝峰（2015）[10]137-142建立基于矩阵距离修正Topsis 的动态赋权模型以确定截面数据的时间权重，弥补了现有Topsis 模型仅能确定指标或者评价对象的权重,无法对不同年份截面数据进行赋权的不足。熵值法模型的应用也已经较为成熟，在企业社会责任研究领域使用广泛（许恒，2018）[11]218-222，而对于赋权方法对比问题，俞立平（2009）[12]154-161分别采用主成分分析、因子分析、TOPSIS 法、秩和比法、灰色关联法、熵权法六种客观赋权法进行排序,然后比较了各种评价结果,为本文的赋权方法对比提供了参考。

关于我国保险企业社会责任表现也有许多实证方面的研究。熊丹丹（2013）[13]24-41采用层次分析法对影响保险企业社会责任绩效评价的因素进行了分析；蔡月祥、王丹丹（2017）[14]58-60通过DEA 模型衡量和比较我国30 家保险企业在2012—2015年的企业社会责任效率，得出我国保险行业企业社会责任效率处于比较低的水平，这也反映了对我国保险企业社会责任进行研究的重要性。

通过梳理相关文献可以发现，无论是投影寻踪模型、Topsis 模型、熵值法模型，还是保险企业社会责任的实证研究，都已有相关文献对其进行论述，这些文献都对本文的研究起到了重要的参考作用。但现有研究仍存在些许不足：一是现有文献并没有对非线性赋权方法和线性赋权方法间的联系与差别进行实证分析，其权重是否存在差异、综合评价值排名有何异同、其结论是否具有一致性和稳定性，这些问题都还没有得到研究；二是现有的对保险企业社会责任进行评价的实证研究都是按年度或仅用平均值之类较为简单的赋权方法得出保险企业社会责任水平值，无法通过给予各年份客观可靠的权重，用一个数值对保险企业多年来的社会责任表现进行评价。基于此，本文关于非线性赋权方法与线性赋权方法间的对比，以及我国保险企业社会责任动态多指标综合评价的实证研究具有重要的理论意义。

三、方法与数据

（一）模型介绍

本文样本数据为涉及企业、时间和评价指标的复杂多维面板数据，需要同时对时间和指标在综合评价中赋权。为了得出各保险企业社会责任的时间、指标权重及最终表现值，本文选取投影寻踪等级评价模型、Topsis 模型和熵值法模型分别作为非线性和线性赋权方法的代表进行对比，以此观察非线性、线性赋权方法是否会造成权重和企业排名的差异。

1.投影寻踪等级评价模型

投影寻踪等级评价模型不要求传统评价方法基于正态分布的假设，通过建立以权重为优化变量的复杂非线性优化模型，在满足总体投影点间尽可能分散且局部投影点间尽可能密集的前提下，寻优获得目标函数最大化的最佳投影方向。运用Matlab 软件的遗传算法工具箱，并采用基于实数编码的加速遗传算法（RAGA）进行优化计算求得最优解。具体步骤如下：

设面板数据有m 个时间长度，n 个指标个数，p 个企业个数，时间段Ti(i=1,2,…，m)，指标为Pj(j=1,2,…，n)，其中效益型指标取原始值，成本型指标取负值，同时假定企业S1(1=1,2,…，P)为有效解，其数据矩阵表示为：X1=（Xij1）mxn，其中某企业l 在i 时间的第j 指标的值表示为Xij1(i=1,2,…，m;j=1,2,…，n)。则面板数据矩阵可以表示为：X=(X1…X1…XP)T。

对面板数据矩阵X 采用规范化方法进行处理：

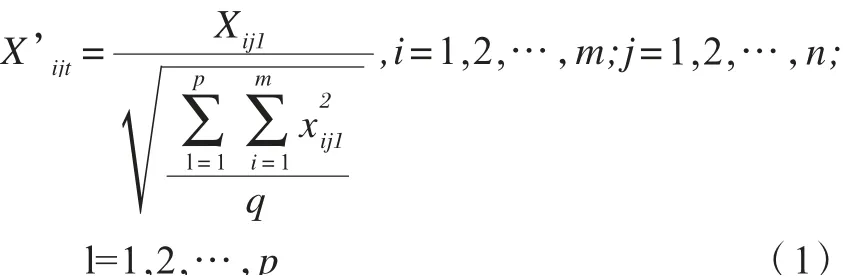
得到规范化矩阵：X'=(X'ijl)mxn，并分别生成最优、最劣方案矩阵，X'+=max｝。 规范化矩阵X'和最优、最劣矩阵X'+、X'-的投影方向：α=（w1,w2,…，wj,…wj,…wn，λ1，λ2…，λi…，λm），并组成向量其一维投影值为：

其中wj(j=1,2,…，n)为第j 个指标的权重；λi(i=1,2,…m)为第i 个时间的权重，构造投影寻踪目标函数：

其中Ez{z(1)|1=1,2,…，q}为投影值序列的平均值，最终建立如下约束非线性优化模型：max Q(α)=Sz,,且wj＞0,λi＞0

2.Topsis 模型

Topsis 模型在找出最优方案和最劣方案的基础上，分别计算各评价对象与最优方案和最劣方案的距离。具体步骤如下：

对截面数据分企业进行评价时，第l 个企业与最优、最劣矩阵的距离分别为：，第l 个企业与最优方案的接近程度Z1 为：。对其时间权重进行赋权时，建立第i 年的评价矩阵Mi，则最优、最劣矩阵即为，则Mi与M+距离为：，与M-距离为的=，则第i 年数据与最优矩阵M+的相对贴近度为

3.熵值法模型

熵的概念源于热力学，是对系统状态不确定性的一种度量。根据此性质，可以利用评价中各方案的固有信息，通过熵值法得到各个指标的信息熵，信息熵越小，信息的无序度越低，其信息的效用值越大，指标的权重越大。具体步骤如下：

（二）数据来源

基于上述模型，由于大部分保险企业公布的年度信息披露报告和社会责任报告集中在2010 年之后，出于数据的可获得性，本文选取时间窗为2010—2016 年的30 家保险企业8 项指标数据为评价样本，构成本文用于分析的面板数据集。本文数据来源于各保险企业年度信息披露报告及年度社会责任报告。本文样本企业特征见表1。

表1 样本选取情况表

四、实证分析及结果对比

（一）保险企业社会责任评价指标体系

本文基于利益相关者理论，结合已有的研究成果，在综合考虑保险企业社会责任特殊性和数据可得性的基础上，基于股东、客户、员工、政府4 个方面①在环保方面的投入只有三家企业有具体数字，因此在本文的研究中，环境方面的因素未纳入。、8 个指标构建了多指标综合评价体系对保险企业社会责任进行评价。具体指标计算见表2。

表 2 保险企业社会责任评价指标体系表

（二）描述性统计

Kolmogorov-Smirnov 检验用来检验单一样本是否来自某特定分布(如正态分布)的一种非参数检验。描述性统计表3 可以看出，从均值、标准差来看，除偿付能力充足率外各指标内部数值差异较大，所有指标的偏度为正，说明样本数据概率密度分布右偏，即低分值部分数据较少，高、中分值数据较多，从峰度看，所有指标都是尖峰的，可以看出中国保险企业社会责任各指标表现总体较好。所有数据的Kolmogorov-Smirnov 检验的p 值均小于0.05，说明数据不符合正态分布，其主要原因为各指标表现较好的数据数量远超于表现较差数据数量，即不论各保险企业具体排名，其社会责任的总体表现都是较为优秀的。

表3 规范化数据描述性统计表

（三）权重对比

按照上述三种模型进行实证研究，结果显示的各指标和时间权重具体见表4①Topsis 模型只能得出综合评价值，不能得出具体指标的权重值，因此表4 中所列仅有Topsis 模型得出的时间权重值没有指标权重值。，从指标权重来看，投影寻踪模型各指标权重较为平均，熵值法模型指标权重较为集中，股东责任（C1+C2）占总权重的一半以上，员工责任（C3+C4）和顾客责任（C5+C6）占比很少；从时间权重来看，除个别年份外，投影寻踪模型的时间权重值随年份m 的增加而表现出较为明显的增长趋势，但两种线性赋权方法却未显示出明显的时间趋势，即不随年份m 的增加而增长。

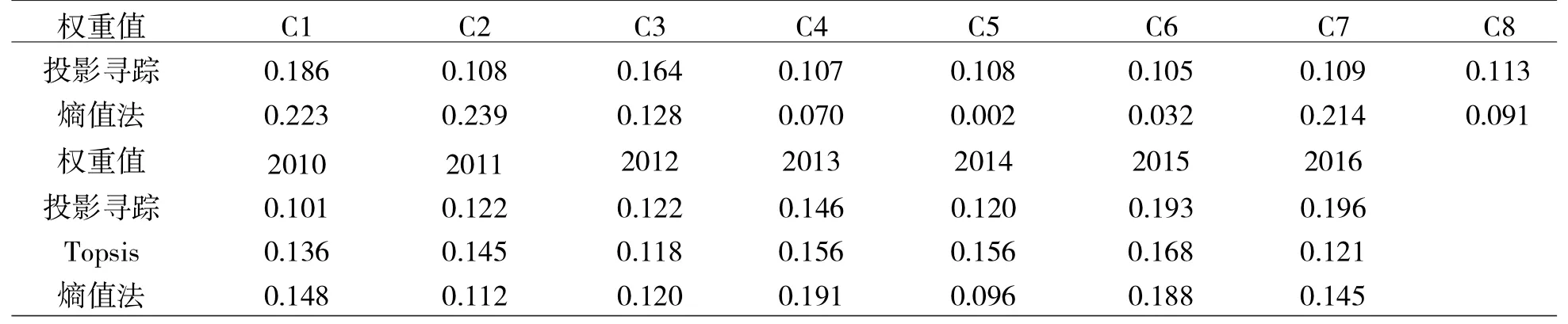
表4 三种模型各指标、时间权重对比表

（四）综合评价值对比

将各指标及时间权重代入数据能得到30 家保险企业社会责任的综合评价值，并通过排序可以得到具体企业名次，如表5 所示，总体上看，三种赋权方法排名之间存在差异，且社会责任表现较好企业的排名差异较大，表现中下的企业排名较一致，这可能由于在特别好与特别差的情况下，评价对象间数据相差较大，容易取得一致的评价结果（俞立平，2009）[12]，说明我国保险企业社会责任表现较好企业间差距不大，表现较差企业与之相比差距较大。但对于三种赋权方法得出的排名是否有分布状态差异，仍需检验证明。

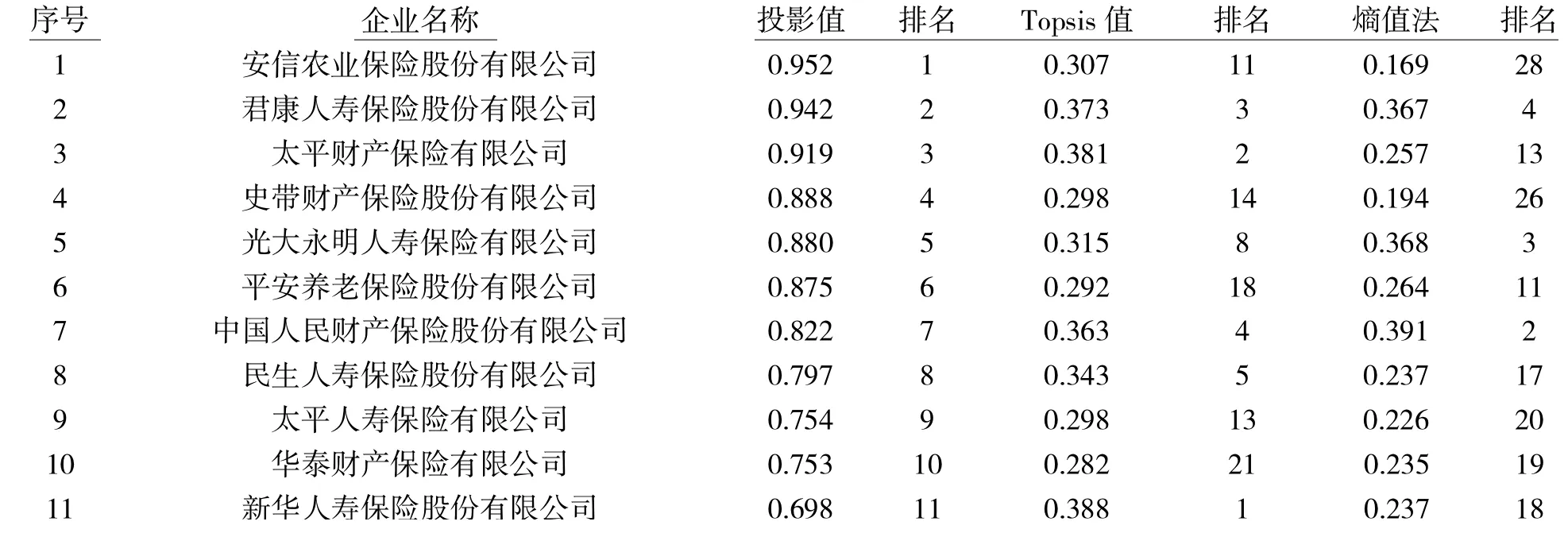
表5 中国保险企业社会责任表现及排名表

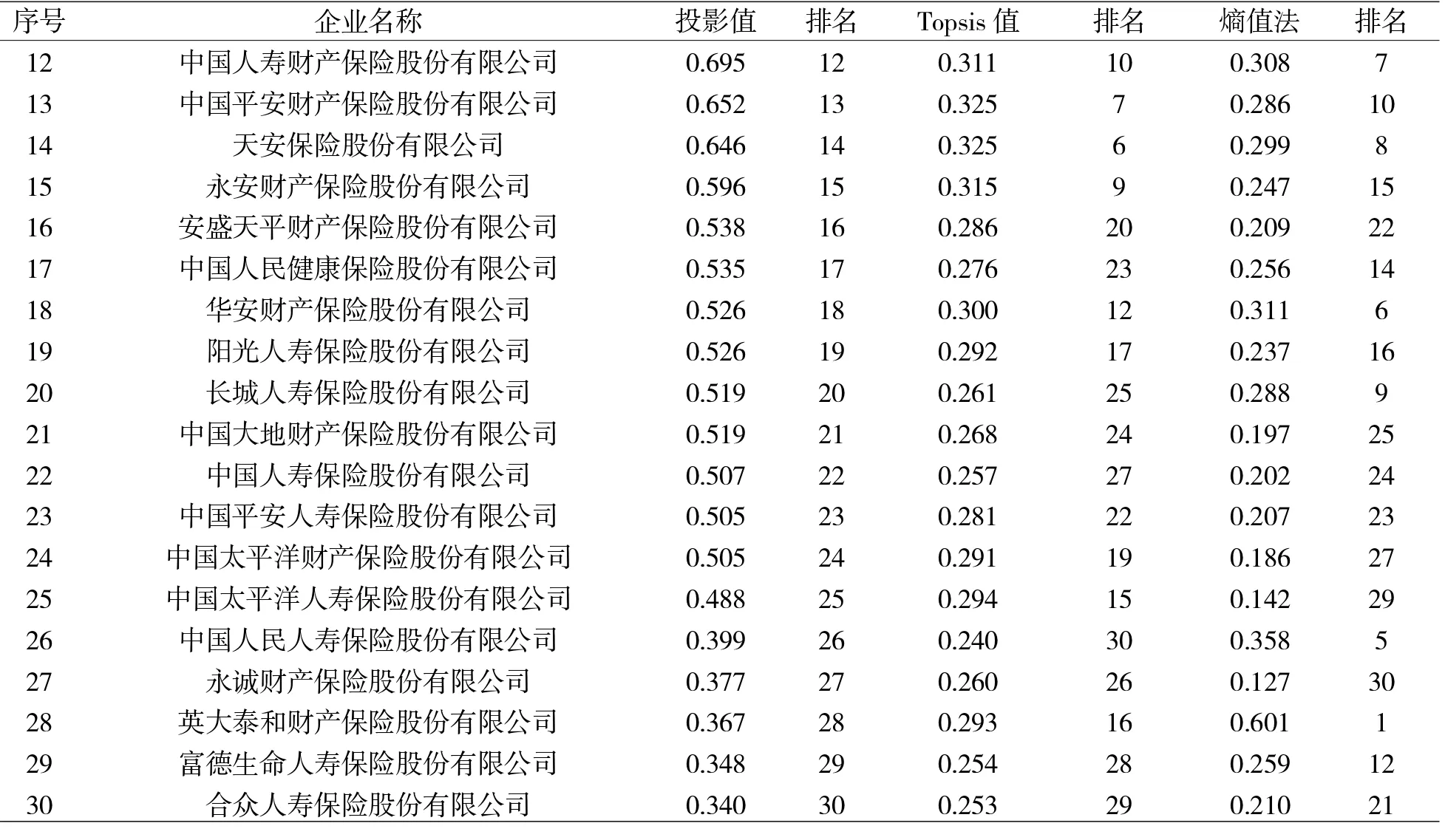
续表5

分别将三种模型得出的排名前15 的保险企业按企业特征进行比例计算，并将结果与全样本比例（表1）相减得出差值，以此分析何种企业特征的保险企业社会责任表现较好。如表6 所示，从企业类别看，国有控股类、外资类及已上市的保险企业社会责任表现较好，非国有控股类、合资类及非上市的保险企业表现稍差；从模型对比来看，三种模型仅在企业性质、股权结构和是否上市这三个企业特征方面得出相同结论，而在险种类别这一企业特征方面存在分歧，Topsis 模型与熵值法模型在险种类别方面得出的结论相反；尽管各类企业特征的保险企业在社会责任方面表现有所差异，但总体差异不大，差值都在10%以内。

表6 排名前15 企业与全样本企业比例差值表

（五）一致性检验

1.Friedman 检验

为了对三种赋权方法的结果进行总体比较，利用SPSS 软件对三种赋权方法得出的排名进行Friedman 检验。Friedman 检验是利用秩实现对多个总体分布是否存在显著差异的非参数检验方法，检验结果Friedman 值为0.475，p 值为0.789，大于0.05 的显著性，不能拒绝3 种评价方法无差异的原假设，即三种评价方法总体上是没有差异的，排序先后都能大致反映出各保险企业社会责任表现差异。但由于各种评价方法实际上相差较大，可以说Friedman 检验在这种情况下是相对粗糙的。

2.Kappa 检验

为了进一步准确比较各模型排名的一致性程度，必须进行Kappa 一致性检验，Kappa 检验是评价两者之间一致性的统计量，将30 家保险企业根据各排序结果按照 2∶3∶5 的比例分为3 个档次，各档次保险企业数量分别为6 家、9 家、15 家。表7 给出了三种模型的二维列联表、Kappa 检验值和一致率。从一致率来看，投影寻踪模型与Topsis模型间一致率最高，而两种线性赋权方法间的一致性最差；从Kappa 值来看，投影寻踪模型与Topsis 模型间的Kappa 值最高，投影寻踪模型与熵值法模型间、Topsis 模型与熵值法模型间的Kappa值都较低，但即使是Kappa 值最高的投影寻踪模型与Topsis 模型，两者的一致性也仅为一般，投影寻踪模型与熵值法模型间、Topsis 模型与熵值法模型间的一致性甚至较差，说明即使三种赋权方法评价出的排名总体分布上无差异，但两两对比下差异仍然很明显，而从二维列联表对角线看，一致的主要集中在第三档次，即排名后15 家的企业，与前文分析一致。

表7 Kappa 检验二维列联及结果表

五、稳定性检验

为了对三种赋权方法进行稳定性分析，本文首先利用聚类分析，将保险企业分为两类；在排除掉企业数目较少的一类企业后，对另一类企业运用原模型分析社会责任评价的排名和得分，并与原来的排名进行比较，从而得到保险企业社会责任排名的稳定性分析。

（一）聚类分析

为了便于剔除企业和提高分析结果的有效性，首先运用聚类分析方法将30 家保险企业分为两类。投影寻踪模型的聚类分析结果将前15 家保险企业归入类别一，后15 家保险企业归入类别二；Topsis 模型将除了第2、3、7、11 家保险企业归入类别一，其余保险企业归入类别二；熵值法模型除了将第1、2、4、5、16、17 家保险企业归入类别一，其余保险企业归入类别二。由于类别二中的保险企业对于保险企业整体的代表性更高，因此本文使用类别二的保险企业数据重新运用原模型进行评价。

（二）模型前后对比

在表8 中，第Ⅰ列表示剔除类别一中的保险企业后类别二中保险企业社会责任的评价排名；第Ⅱ列表示第Ⅰ列和剔除掉类别一的保险企业后，类别二的保险企业在原来30 家保险企业中的相对排名差的绝对值。可以看出，除了极个别企业外，在去掉类别一保险企业后，运用原模型进行评价保险企业的社会责任排名变化不是很大。

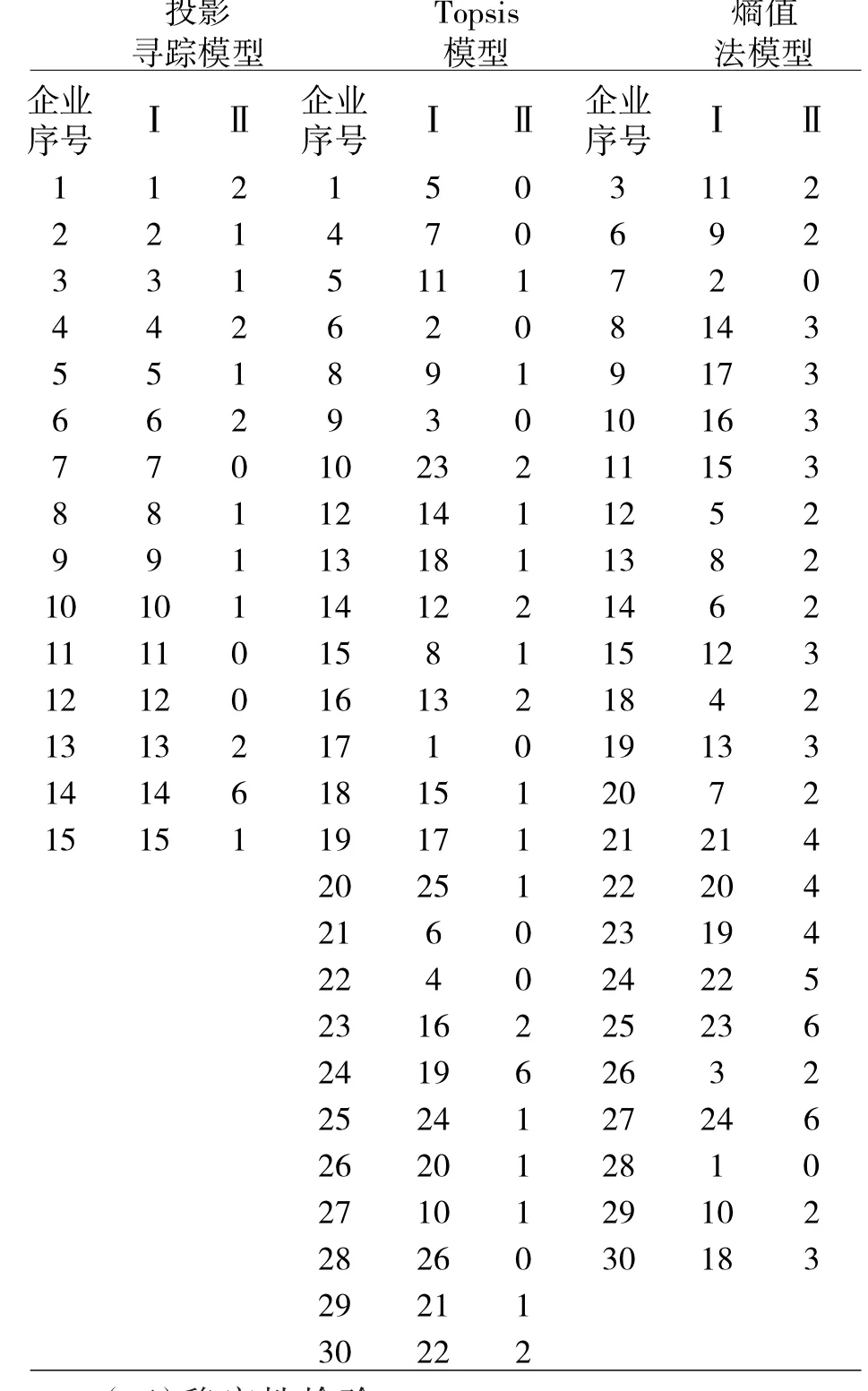
表8 三种模型聚类前后对比表

（三）稳定性检验

运用Wilcoxon 符号秩检验对保险企业社会责任评价结果的稳定性进行检验。由表9 的结果可得：双侧显著性水平均为0，即类别二中原模型保险企业排名的结果与剔除掉类别一的企业后，类别二的企业在原来30 家企业中的相对排名属于同分布，证明三种赋权方法得出的保险企业社会责任评价结果皆通过了稳定性检验，具有稳定性。

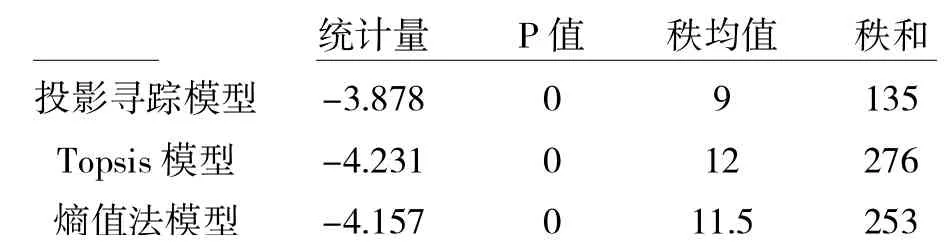
表9 模型聚类前后的稳定性检验

六、结 论

本文基于2010—2016 年中国30 家保险企业社会责任表现的面板数据，按照利益相关者理论，通过建立综合评价指标体系对其进行动态多指标综合评价，并分别运用投影寻踪模型、Topsis 模型和熵值法模型作为非线性与线性赋权方法的代表进行实证分析与方法对比，显示出不同赋权方法得出的权重及排名间的差异，并通过Friedman 检验、Kappa检验和聚类后再评价、Wilcoxon 符号秩检验的方法分别对三种赋权方法进行一致性检验和稳定性检验，证明其排名是客观稳定的。具体结论如下：

首先，三种赋权方法对于本文样本数据来说确实是客观而稳定的，其排名结果虽然在总体上无分布差异，但三种赋权方法两两对比来看差异还是较为明显，具体来看，投影寻踪模型与Topsis 模型间的一致性相对较好，投影寻踪模型与熵值法模型间、Topsis 模型与熵值法模型间的一致性相对较差，在这一点上，并不存在线性赋权方法结论一致，线性赋权方法与非线性赋权方法结论不一致的现象，甚至在部分结论上，还存在两种线性模型得出的结论相反的情况。

其次，社会责任表现较好企业的排名在不同赋权方法下差异较大，表现中下企业排名较一致，可能由于在特别好与特别差的情况下，评价对象间数据相差较大，容易取得一致的评价结果，这一方面，三种赋权方法得出的结论较为一致。

再次，从指标权重来看，投影寻踪模型各指标权重较为平均，熵值法模型指标权重较为集中；从时间权重来看，除个别年份外，投影寻踪模型的时间权重值随年份m 的增加而表现出较为明显的增长趋势，但两种线性赋权方法却未显示出明显的时间趋势，即不随年份m 的增加而增长，在这一点上，出现线性赋权方法结论一致，线性赋权方法与非线性赋权方法结论不一致的现象。

最后，从样本结果来看，我国保险企业社会责任存在总体表现较好，表现好者之间差异小，与表现差者差异大的特点。从企业特征看，我国保险企业社会责任表现出国有控股类企业强，非国有控股类较弱；外资类企业强，合资类较弱；上市企业强，非上市企业较弱的特征。

总而言之，非线性赋权方法与线性赋权方法间得出的结论既存在差异，也有一致之处，线性赋权方法间得出的结论也是存在差异的。此外，本文在赋权方法的选择上只是选择了三种模型作为非线性赋权方法与线性赋权方法的代表进行实证研究，对其他同类评价方法并未涉及，可能使本文结论不很全面，希望本文能为以后学者的相关研究提供方向和借鉴。