膨胀腔类超材料的传递损失∗

邢 拓 李贤徽 盖晓玲 蔡泽农 王 芳 关淅文

(北京市劳动保护科学研究所 环境噪声与振动北京市重点实验室 北京 100054)

0 引言

声学超材料及结构因其良好的声学性能，或其较小的结构尺寸等受到学者广泛关注。声学超材料一般是由人工微单元构成的复合材料或复合结构，从而实现自然材料不能实现的功能。声学超材料的常见微单元包括：薄膜型[1]、Helmholtz 共振型[2]、Mie 共振型[3]、卷曲空间型[4]、五模式型[5]等。其中复合背腔的薄膜型、卷曲空间型、Mie 共振型和Helmholtz 共振型及其组合结构中通常都包含膨胀腔或类似结构。以近期的研究为例，Jia 等[6]设计的宽带卷曲路径声学超材料，实现了1400∼2860 Hz的宽带隔声，其中卷曲路径设计中包含膨胀腔和收缩腔结构。Krushynska 等[7]设计了卷曲通道的迷宫声学超材料，用于低频噪声控制。Noguchi 等[8]对声弹性耦合系统中负体积模量的声学超材料进行了优化设计。Long 等[9]利用Helmholtz 腔结构在373 Hz 实现了完美吸声，并使用多Helmholtz腔实现了拓宽带宽的目的，Jiménez 等[10]也利用Helmholtz 共振腔实现了超薄的完美吸声和准全向吸声。该类超材料设计中都含有膨胀腔结构或类似结构，同时超材料因其复杂的结构或较小的尺寸，通常使用3D 打印技术实现。由声固耦合所导致的声学效果与设计效果不符的情况时常存在。因此本文针对含有膨胀腔类的超材料，研究了声固耦合对其声学性能的影响。

另一方面，在实际应用中膨胀腔常见于抗式消声器结构中。膨胀腔结构分为简单膨胀腔和复合膨胀腔，其中简单膨胀腔结构如图1所示。膨胀腔消声器及其扩展结构已被广泛研究。Selamet等[11]用频域分析方法研究了穿孔管消声器。Middelberg等[12]将二维对称时域方法引入到消声器计算中。康钟绪等[13]研究了膨胀腔消声器一维声学仿真中的修正方法，对管道末端修正系数进行了研究。刘晨等[14]利用CFD 方法对有流的穿孔管消声器进行了三维计算，结果表明，随着气流增加，传递损失(Transmission loss, TL)向低频移动。方智等[15]利用数值模态匹配法，研究了插管结构对膨胀腔消声器声学性能的影响，结果表明该方法的结果与有限元仿真结果基本吻合。苏胜利等[16]利用CFD时域仿真和实验的方法，研究了双级膨胀腔消声器的声学性能。赵晓臣等[17−18]研究了鼓型消声器(膨胀腔加膜结构)的声学性能理论计算，通过计算膜结构的振动速度，得到鼓型消声器的传递损失。孟贝[19]针对车用消声器的声固耦合进行了研究和分析，结果表明声固耦合可能导致的减噪量曲线出现了明显的突变点。

图1 简单膨胀腔结构Fig.1 Simple expansion chamber

无论对于超材料结构还是广泛使用的膨胀腔消声设备，一般理论计算都是从声学基本方程出发，将结构看成刚性结构，而在实际结构中声固耦合问题完全存在，特别是对小、薄和复杂的超材料结构的影响更大。因此需要考虑声固耦合对结构声学性能的影响，为了简化研究内容，仅将超材料结构简化为膨胀腔结构。以膨胀腔结构为研究对象，定义传递损失来评价该结构的声学性能，利用有限元方法分析刚性结构和考虑声固耦合结构的传递损失现象，讨论了声固耦合对于结构隔声性能改变的优缺点。

1 膨胀腔的传递损失分析

简谐声场在膨胀腔内的控制方程为

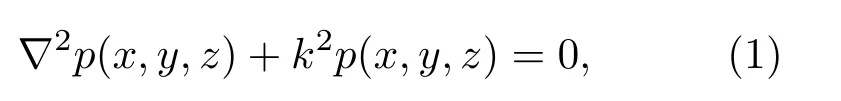
其中，∇2=∂2/∂x2+∂2/∂y2+∂2/∂z2是笛卡尔坐标系下的拉普拉斯算子，p为声压，k=ω/c0为波数，ω是角频率，c0为声速。

利用有限元方法可以将方程(1)的解表示为

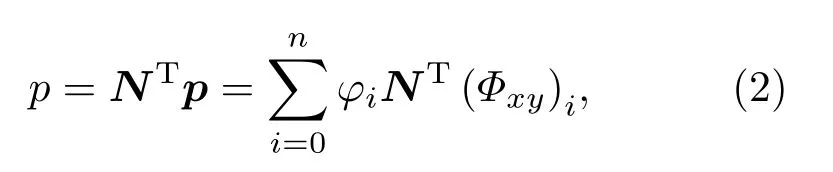
其中，N是广义形函数的列向量，p是节点水平方向声压分量的列向量，φi是第i阶模态的幅值系数，(Φxy)i代表第i阶横向本征波数。

当考虑声固耦合作用时，其对应膨胀腔壁面处的边界条件为

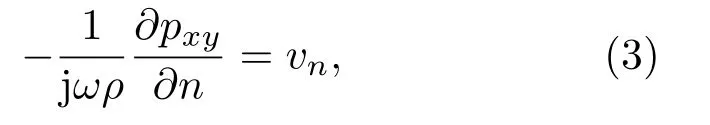
其中，∂pxy/∂n表示沿外法线方向的导数，ρ为介质密度，vn是壁面边界的法向振动速度。

结合边界条件式(3)，应用伽辽金加权残数法可以得到如下有限元方程[20]：

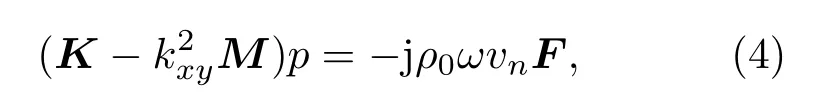
结构固体域的控制方程可以写为[21]

其中，ρs为固体密度，u是节点位移场，S是结构应力，S=C(E,ν):ε，E是杨氏模量，ν为泊松比，“:”代表张量积，是结构的应变，kz为平面外波数，λ是Lamé参数。声-结构耦合边界的耦合方程：

其中，n是表面法向方向，utt代表结构加速度，FA为结构载荷。

当背景压力场选择平面波入射时，可具体表示为

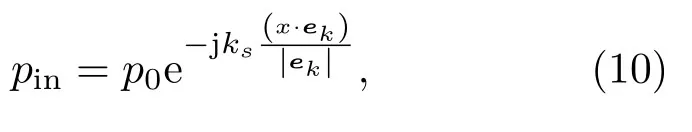
其中，pin入射平面波声压，p0是声压振幅，ks为波数，x是边界位置，ek为方向波矢量。

因此，该膨胀腔的传递损失可以写成：

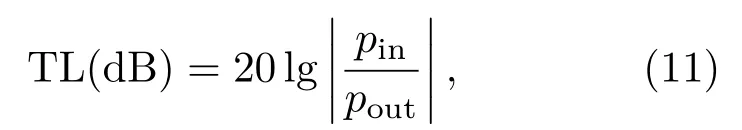
其中，pout为声波通过结构后的输出声压。

2 模型建立及实验方案

针对声固耦合问题通常采用有限元的方法计算，将模型剖分后把网格节点的振动和声压联系起来，把结构振动作为边界激励条件，将边界振动转化为声压的波动，再用边界振动矩阵去修正结构的刚度矩阵，达到求解目的。

2.1 模型建立

二维简单膨胀腔结构如图1所示，其实际结构采用3D 打印技术制成，其原材料为低黏度光敏树脂。该结构的密度是1200 kg/m3，杨氏模量为2×109Pa，泊松比为0.41。空气密度为1.2 kg/m3，声速340 m/s。有限元模型利用COMSOL Multiphysics 建立，共包含两种模型，一种是未考虑结构振动的原始设计模型，另一种是考虑结构振动的声固耦合模型。其中声固耦合模型如图2所示，该模型分为固体域和压力声学域两部分。对于固体域部分，结构的上下端口处，采用固定约束处理。压力声学域部分包括：完美匹配层、背景压力场和空气层构成，具体见图2中标示。背景压力场选择振幅为1 Pa的垂直向下入射平面波。完美匹配层采用六面体网格剖分，膨胀腔和其他空气层均采用自由四面体网格剖分，共计求解自由度数为728409。

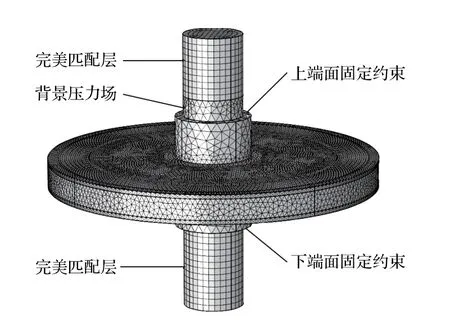
图2 膨胀腔消声器的有限元模型Fig.2 Finite element model of expansion chamber silencer

2.2 实验方案

该膨胀腔结构的主要设计隔声范围为800∼1200 Hz，其实际结构如图3所示，其中左边为加厚结构，右边为普通结构。利用B＆K公司4206型阻抗管系统，测试该样品的传递损失。所有结构的管道直径为29 mm，管道伸出长度为20 mm，结合膨胀腔的设计要求，确定膨胀腔内部直径为150 mm，膨胀腔内部空气层厚度为10 mm，普通结构壁厚为2 mm，加厚结构壁厚为6 mm。该测试系统采用四通道传递函数法测试，选择小管(直径29 mm)测试系统，将3D 打印样品与阻抗管系统连接，如图4所示。

图3 膨胀腔3D 打印结构Fig.3 3D printing expansion chamber

图4 实验测试系统Fig.4 Experimental test system

3 结果及讨论

3.1 结果

膨胀腔结构的传递损失测试结果如图5所示，其中普通膨胀腔结构出现了明显的声振耦合现象，该结构在设计频段(800∼1200 Hz)并未实现良好的隔声效果。为了分析其声固耦合现象，对普通膨胀腔结构进行了声固耦合的有限元仿真，其传递损失结果与普通膨胀腔的测试结果基本吻合。通过加厚膨胀腔的侧壁，结构的传递损失与设计结果基本吻合，达到了目标频段的隔声目的。具体而言，普通膨胀腔测试结果出现了两个明显的峰值，分别是654 Hz 和1170 Hz，其中在829∼1070 Hz 的范围内，传递损失低于10 dB。加厚膨胀腔的传递损失在983 Hz 附近达到34 dB，其中传递损失在810∼1220 Hz 的频段内，传递损失不低于15 dB，与刚性结构仿真结果基本一致。仿真结果与实验结果存在差别的主要原因是，仿真计算中是完全固定约束，而在实际测试中不可能实现完全的固定约束。除此之外，在实验测试中连接处的结构振动也可能导致实验结果与仿真结果存在差别。实验测试的传递损失实际包括三种能量损耗：结构的真实传递损失、由密封性所导致的能量损耗和侧壁与外部空气的振动耦合导致的能量损耗，其中侧壁与外部空气振动耦合所导致的能量损耗一般可以忽略。测试结果的峰值小于仿真结果的峰值，主要是由于结构密封性能导致的。

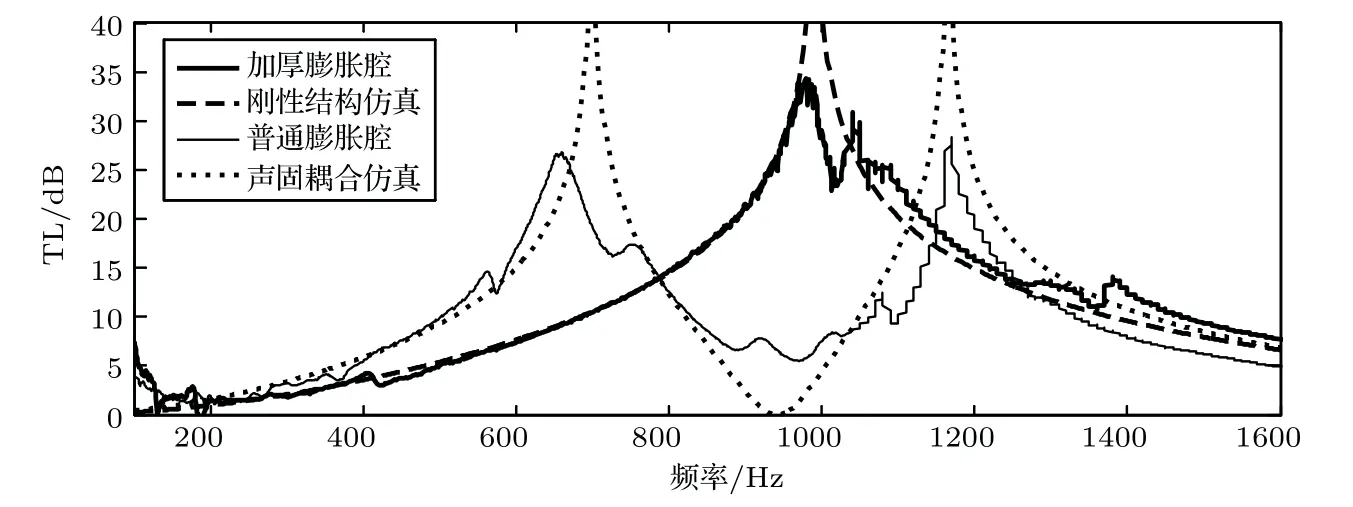
图5 实验与仿真结果Fig.5 Experiment and simulation results

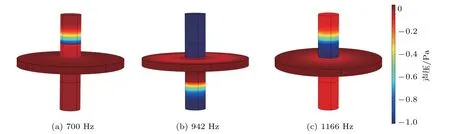
图6 声场结果Fig.6 Sound field results

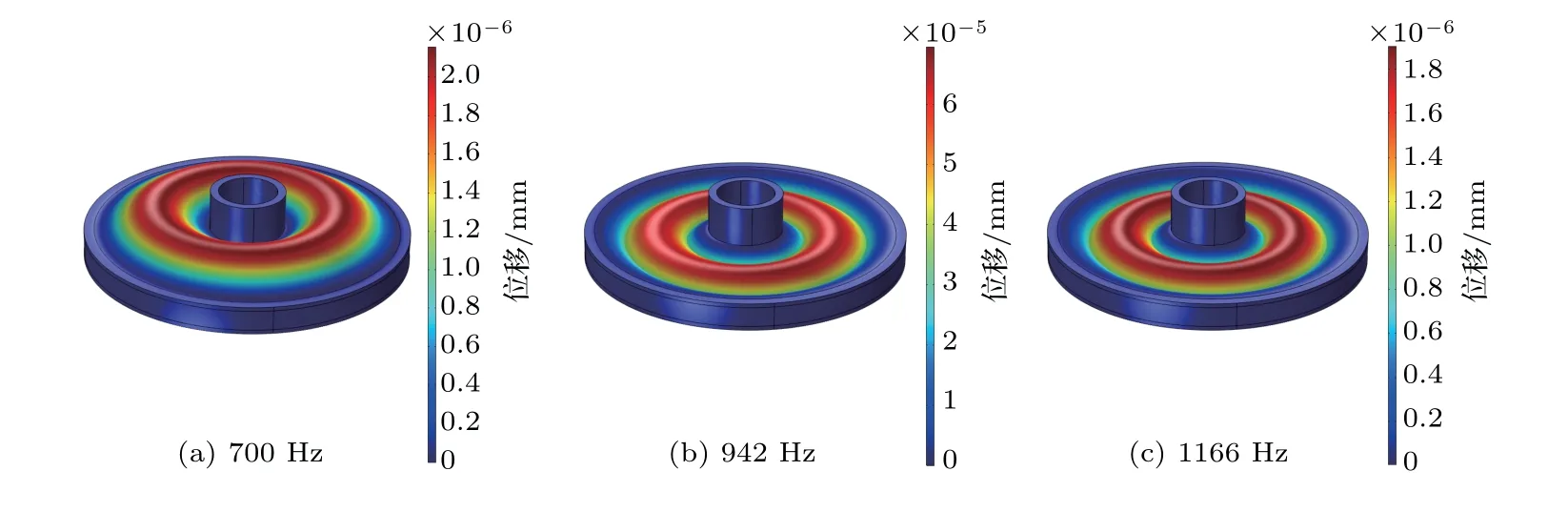
图7 膨胀腔位移Fig.7 Displacement of the expansion chamber

从图5可知，对于普通膨胀腔的声固耦合仿真结果的两个峰值所对应频率为700 Hz 和1166 Hz，谷值所对应频率为942 Hz，在该峰值和谷值频率下的声场如图6所示，与之对应的膨胀腔的总体位移如图7所示。从图6可知，声波在700 Hz和1166 Hz处，表现出了明显的反射现象；声波在942 Hz 处完全透射过结构，传递损失为零。同时，声波在700 Hz和1166 Hz 处反射现象所产生的驻波位置并不相同，其中1166 Hz 处的反射声波所形成的驻波在管口处。从图7可知，结构在942 Hz 处的最大位移达到了约7×10−5mm，而结构在峰值处的最大位移达到了约2×10−6mm，说明结构在谷值处与声波发生完全共振，结构作为媒介传递了声波能量。同时在700 Hz 处的位移方式与另外两个频率下的位移方式不同。

3.2 讨论

膨胀腔的侧壁厚度变化对传递损失的影响如图8所示，通过增加其侧壁厚度可以有效减小声固耦合现象对传递损失的影响。随着侧壁厚度的增加，传递损失的第一、第二峰值向高频移动。当壁厚达到6 mm 时，传递损失的第一峰值所对应频率与设计结果的第一峰值所对应频率基本一致。另一方面，声固耦合现象也可以被设计作为一种低频隔声结构，特别是对于强声固耦合作用的引入，如：弹性板或者膜类结构，从而突破刚性结构的设计频段范围，实现更低频隔声效果。

通过改变原薄壁膨胀腔的内径尺寸，研究其声固耦合对结构的传递损失影响，其结果如图9所示。分别选择了内径为120 mm 和90 mm 的膨胀腔结构进行声固耦合分析和单声场分析。结果表明：当膨胀腔内径为120 mm 时，结构的声固耦合对传递损失影响较大；当膨胀腔内径为90 mm 时，结构的声固耦合对传递损失影响较小。在不考虑声固耦合影响时，120 mm 内径的膨胀腔的传递损失峰值在1370 Hz；当考虑声固耦合影响时，其传递损失的峰值分别在1211 Hz 和1670 Hz，两者传递损失峰值的出现位置差别明显。在不考虑声固耦合影响时，90 mm 内径的膨胀腔的传递损失峰值在2149 Hz；当考虑时，其传递损失的峰值为2113 Hz，两者差别较小。因此缩减内径可以减小声固耦合对传递损失的影响。但一般声学超材料结构是针对低频噪声源，缩减内径会导致结构的隔声峰值向中高频移动，所以该策略的使用需要权衡考虑。

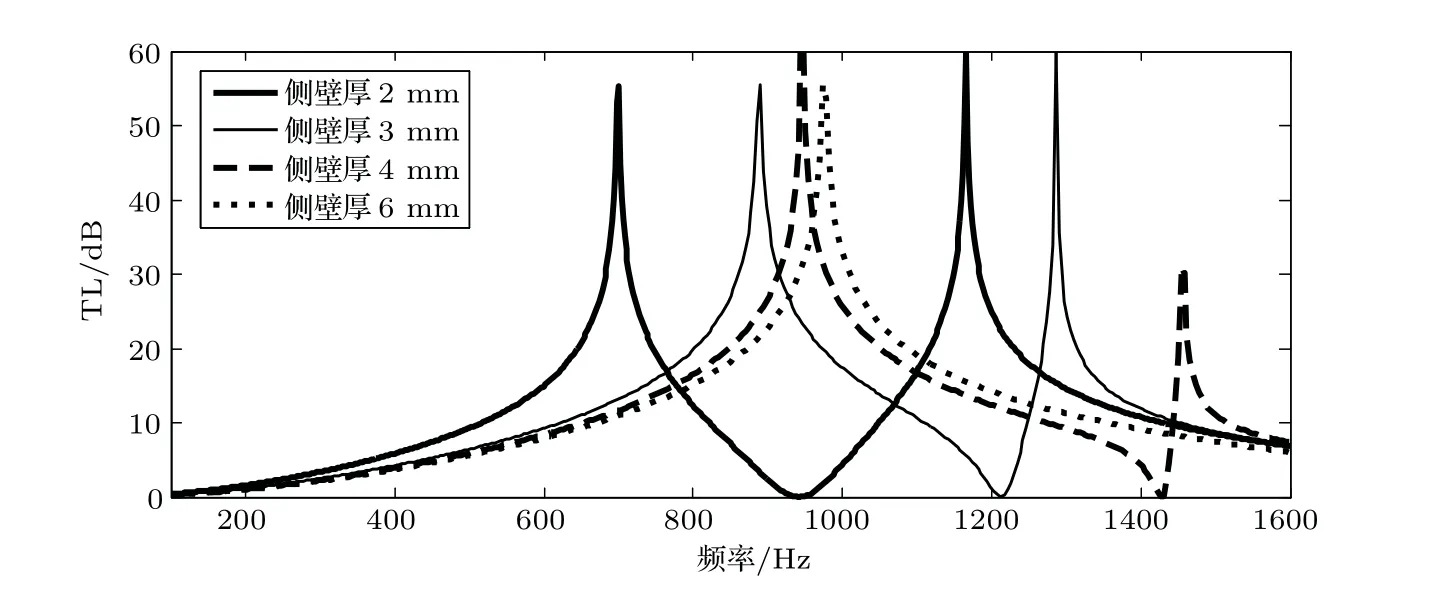
图8 不同侧壁厚度对传递损失的影响Fig.8 Influence of sidewall thickness on TL

图9 不同内径对传递损失的影响Fig.9 Influence of inner diameter on TL

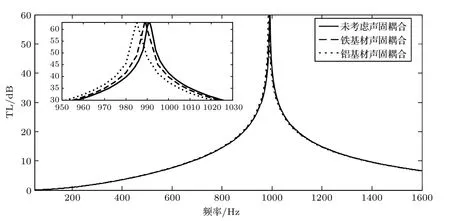
图10 不同材料对传递损失的影响Fig.10 Influence of materials on TL

另一方面，改变膨胀腔的加工材料也可以减弱声固耦合对其传递损失的影响，其结果如图10 所示。选择与原薄壁膨胀腔相同的结构尺寸，分别选择铁和铝作为3D 打印基材，分析其声固耦合对传递损失的影响。结果表明：当铝和铁作为基材时，声固耦合对结构传递损失的影响较小。在大部分工业使用场合选择这两种金属基材时，该尺寸下结构的声固耦合基本可以忽略不计。同时也表明，材料的刚度越大，声固耦合对结构的影响越小。

4 结论

膨胀腔类超材料结构的声固耦合现象广泛存在，采用有限元计算结合阻抗管实验的方法，得到了其传递损失，分析了该现象对传递损失的影响。研究结果表明：2 mm 厚3D打印膨胀腔结构存在明显的声固耦合现象，增加结构厚度后，声固耦合对其传递损失的影响减弱；通过增加膨胀腔的壁厚，其传递损失与设计结果完全吻合；采用声-结构耦合仿真计算方法得到的传递损失与未加厚膨胀腔消声器的实验结果基本吻合；采用增加壁厚、缩小内径或选择金属材料的方式，都能使得声固耦合对传递损失的影响减弱。以上结果说明，当刚度较小或者面积较大时，对超材料结构进行声固耦合分析是完全必要的。