基于聚焦换能器的超声透射CT技术∗

蒋 剑 王月兵 沈 超 郑慧峰

(中国计量大学计量测试工程学院 杭州 310018)

0 引言

超声透射CT是一种利用超声波对被测物体进行不同角度的投影测量而获取物体横断面信息，并通过相应的算法重建物体内部结构的成像技术。由于该技术具有无电离辐射、价格便宜、分辨率高、成像结果直观等优点，被广泛应用于医学诊断和工业检测等领域[1−2]。

当物体一侧的超声发射器发出一个脉冲信号后，另一侧的接收器可在一定时延后接收到该脉冲信号，这个时延就是物体存在时的超声波走时，若将物体移去，可得另一超声波走时。利用各角度超声波穿越有物体的走时与穿越无物体的走时之差，可以重建物体断面上的声速分布图像，而获得精准的走时差是重建出高质量图像的前提[3]。Mitsui 等[4]采用峰值法提取发射信号至接收信号的走时；Li 等[5]开发了AIC 自动时间采集器，并采用加权平均模型的方法获取走时，但上述方法只适用于信噪比较高的情况。在图像重建算法方面，目前主要有变换法和迭代法两大类[6−7]，已有的研究多通过数值仿真去对比两类算法的优劣[8]，很少从成像实验的角度加以分析。

鉴于此，本文利用弧形线聚焦换能器作为发射器和接收器对物体进行CT 检测，证明其能够提高信噪比，进而可以高效地获取较精确的投影数据，并采用滤波反投影(Filter back projection,FBP)和最小二乘正交分解(Least squares QR-factorization,LSQR)两种算法重建物体横断面图像，对比确定更优的检测方法。

1 原理与方法

1.1 弧形线聚焦换能器焦域分析

如图1所示，弧形线聚焦换能器的辐射声场在焦域处具有足够的能量密度，且聚集在一定大小的薄切片内，该聚焦切片内的声束近似于平行波束，与X 射线CT 相仿[9]。当聚焦切片厚度极小且被测物体恰好处于切片之内时，声波穿越物体所得到的投影数据能够真实地反映物体横截面的情况；同时，由于波束平行且聚集性能好，在物体另一侧用同样的聚焦换能器所接收到的直达波信号是由诸多聚焦波束同相叠加的结果，相比发散波束而言，其信号幅值更大，信噪比更高。但若被测物体大小超出聚焦切片的范围，如图2所示，则会适得其反，因为声波在进出物体的前后，波束不够平行，散射现象较为严重，获取的投影数据会有较大偏差。因此，充分利用聚焦切片区域对物体进行CT 成像，可以提高成像质量。但由于聚焦换能器的几何尺寸影响着聚焦切片的尺寸大小，同时聚焦切片在Z轴方向上的宽度zw决定着适用的被测物体的尺寸；在Y轴方向上的宽度yw决定着投影数据的精确度，故选择合适的聚焦换能器尺寸进行超声CT检测至关重要。

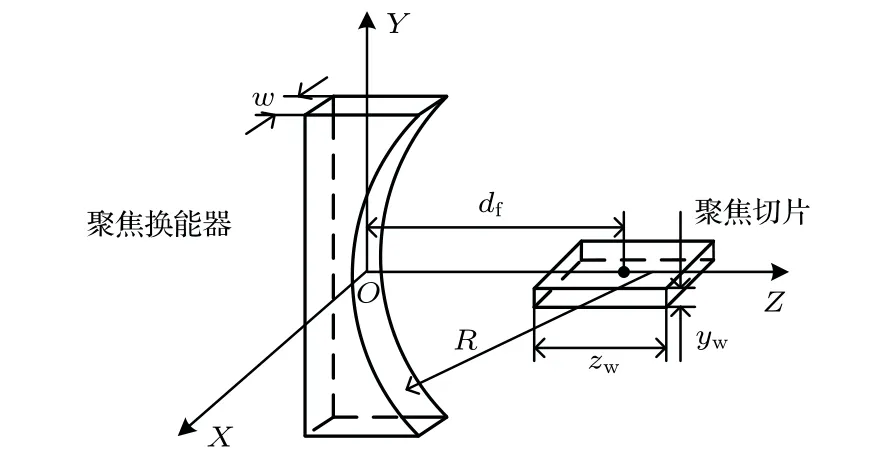
图1 弧形聚焦换能器及其焦域示意图Fig.1 Schematic diagram of the arc focused transducer and its focal region

图2 被测物体所处位置示意图Fig.2 Schematic diagram of the measured object position

为了探究聚焦切片尺寸与聚焦换能器几何尺寸的关系，对上述弧形聚焦换能器进行声场计算，如图3所示。计算中取换能器的张角α= 70◦，宽度w= 6 mm，曲率半径R= 35 mm，工作频率f= 1 MHz，水中声速c= 1500 m/s。从Rayleigh积分公式出发，在积分计算时，把被积函数中的简单球面波函数亦即无限介质中点源的Green 函数，按波分解的方法变换为各角谱分量的迭加，也就是Sommerfeld 积分，那么，空间中场点Q(x,y,z)的速度势函数ϕ(Q)可表示为[10]

式(1)中，J0(uξ)为第一类零阶贝塞尔函数，u为Sommerfeld 积分公式中引用的一个积分变量，其具体形式参见文献[11]和文献[12]，L为发射面元S点到场点Q的距离，ζ是场点Q到G点的距离(G点为垂直于平面X=X0并经过S点的直线与平面X=X0的交点)，满足关系式：为波数，A为换能器表面S点面元到X轴的距离，v为换能器表面质点振动速度，而声压p(Q)的表达式为

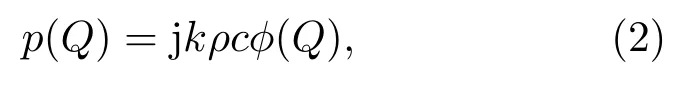
式(2)中，ρ为介质密度。

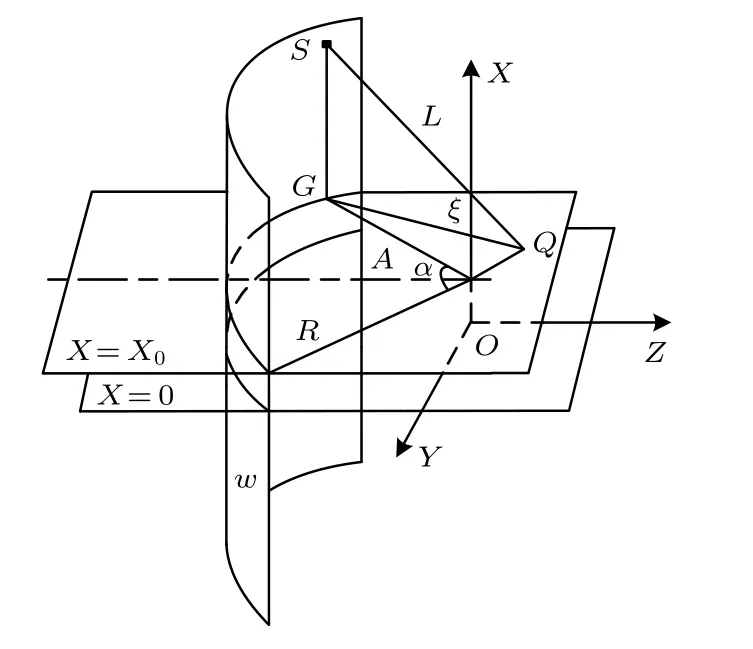
图3 弧形聚焦换能器坐标系Fig.3 Coordinate system of the arc focused transducer

通过式(2)能够计算聚焦换能器水下声场中任意位置的声压分布，如图4所示，为聚焦换能器焦点处各方向线上归一化后的声压分布。从图4中可以看出：Y轴与Z轴方向上的声压仅有一个主峰值，其中，Y轴方向上峰的宽度很窄，峰值之外声压下降很快，展现出了良好的聚焦性能，表明声场在焦域处形成了聚焦切片，声能量主要集中在该切片内，切片越薄，对检测越有利；Z轴方向上峰的宽度较宽，正是这个宽度决定着超声CT能够检测的物体尺寸大小；而X轴方向上的声压从中心往两侧逐渐减小，速率较慢，波束宽度很大，表明声能量不集中，较为发散，但在超声CT检测过程中，接收端只是在某一位置接收直达波信号，该方向上声束的发散对检测结果的影响并不大，故不对X轴方向上的波束宽度作讨论。

为了求解聚焦切片的尺寸大小，计算各方向上主瓣最大幅值下降6 dB 的声能量主要集中的范围大小即可[13]。计算得到聚焦切片Y轴方向上的宽度yw为1.5 mm，Z轴方向上的宽度zw值为9.7 mm。通过改变聚焦换能器的张角α和曲率半径R，探寻以下关系：

(1) 当曲率半径R为35 mm 一定时，聚焦换能器张角α与换能器声焦距df、聚焦切片Z轴方向上的宽度zw和Y轴方向上的宽度yw的关系，如表1所示；

(2) 当张角α为70◦一定时，聚焦换能器曲率半径R与换能器声焦距df、聚焦切片Z轴方向上的宽度zw和Y轴方向上的宽度yw的关系，如表2所示。

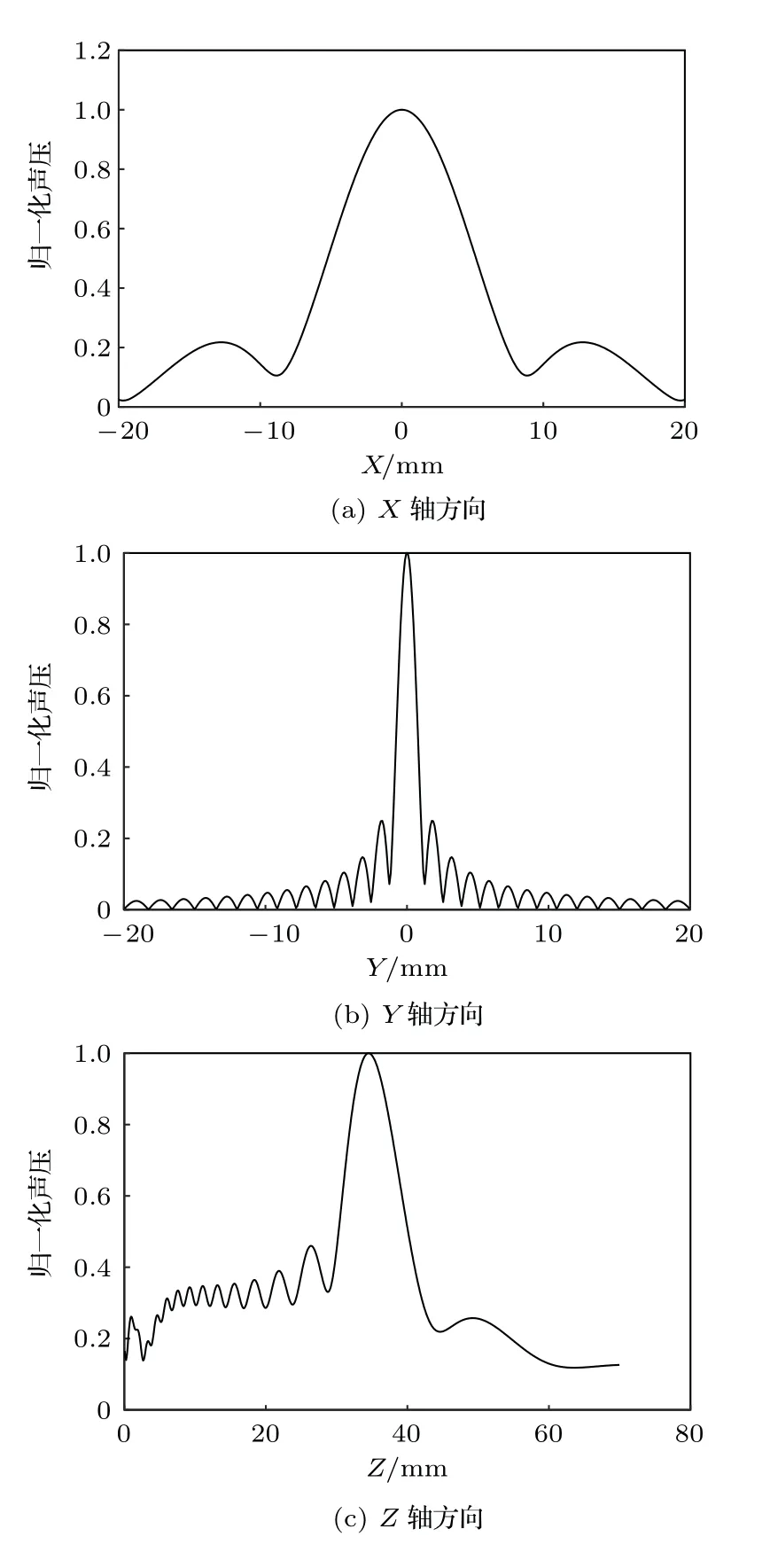
图4 不同方向上归一化声压分布图Fig.4 Normalized sound pressure distribution in different directions

从表1和表2可以看出，该弧形聚焦换能器曲率半径一定时，其张角越大，聚焦性能越好，但是在焦域处波束的平行性越差，使得检测的准确性降低；而在换能器的张角一定时，其曲率半径越小，聚焦性能越好，但是在焦域处的平行波束范围越小，可以用于检测的物体尺寸较小，故在选择聚焦换能器时需要权衡zw和yw两个焦宽取值，才能取得理想的成像结果。

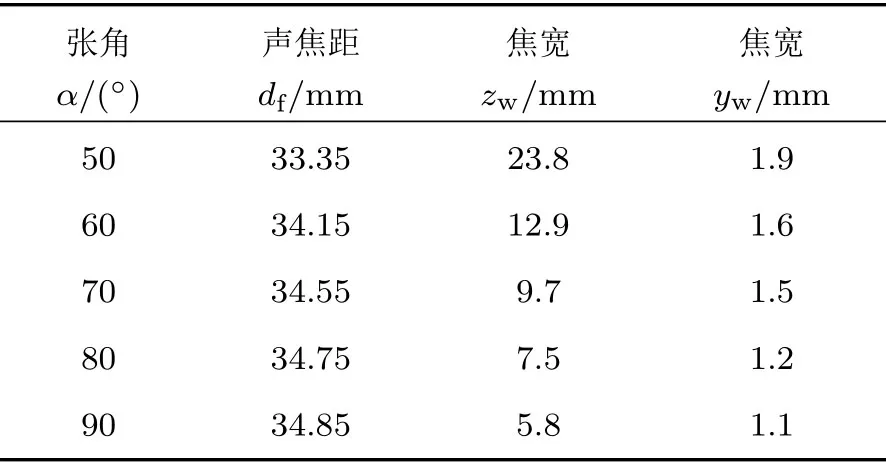
表1 张角大小与聚焦切片尺寸的关系Table1 The relationship between open angle and focused slice size

表2 曲率半径与聚焦切片尺寸的关系Table2 The relationship between radius of curvature and focused slice size

1.2 超声透射CT检测方式

为了获得足够多的投影数据，采用等角扇形束并模拟“单发多收”的扫描方式进行检测。如图5所示，考虑到聚焦换能器的声场特性并利用其焦域对物体进行检测，设计发射换能器与接收换能器到旋转中心O点的距离均为声焦距df。检测时，将被测物体放置于旋转中心O点处，发射换能器以β角为旋转步长发射信号，接收换能器以γ角为旋转步长接收信号，当发射换能器发射一个脉冲信号后，接收换能器通过旋转依次接收多点信号，直至完成一个覆盖角为θ的扇形束扫描，进而实现“单发多收”，相比传统的平行束等扫描方式，能够提高检测效率[14]，节约成本。通过扫描，能够获取(θ/γ)×(2π/β)个投影数据，若旋转步长足够小，则获取的投影数据越多，重建图像的质量越高。

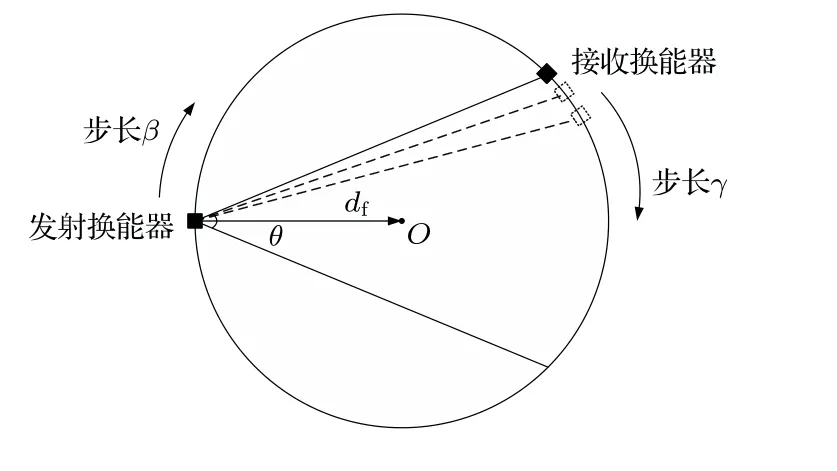
图5 扫描检测示意图Fig.5 Schematic diagram of scanning detection

2 实验研究

2.1 实验系统及条件

选取内径4 mm、外径6 mm的环状笔芯作为被测样品，为了保证被检样品处于聚焦切片之中，且能够获取较高准确度的投影数据，由表1和表2可知，利用张角α为70◦，宽度w为6 mm，曲率半径R为35 mm 的弧形聚焦换能器进行检测实验是合适的。实验系统如图6所示。水箱的大小为50 cm×50 cm，用来浸泡样品，且水介质有助于信号的传输。为了减少声波反射等干扰，需要在箱体边缘放置吸声材料。收发换能器能够在旋转台0、1 的驱动下做360◦的旋转，其中发射换能器以1◦的旋转步长发射信号，接收换能器以1◦的旋转步长接收信号，扇形束的覆盖角为58◦；信号发生器发射频率为1 MHz 的正弦填充脉冲信号，经过功率放大器后产生两路信号，一路驱动发射换能器工作，另一路作为同步信号被采集，后期用来提取超声波的走时；接收换能器接收到的携带物体断层信息的超声信号经前置放大器后，由计算机控制采集并进行数据处理。由于本实验所用超声波信号的频率为1 MHz，对应的波长为1.5 mm，而声衍射的强弱是同障碍物的大小与声波波长的比值密切相关的，一般采用ka= 2πa/λ的值来描述，其中，k为声波的波数，λ为声波的波长，a是代表障碍物相对尺度的量。ka的值越小(ka ≪1)，声衍射现象越强；ka的值越大(ka ≫1)，声衍射现象越弱。若取被测样品的尺度a= 3 mm，可计算出ka= 12.57≫1，说明声波衍射效应较弱，那么，接收换能器接收到的声波信号中，无用的干扰信号较少，波形结果更能准确反映被测样品截面的信息。

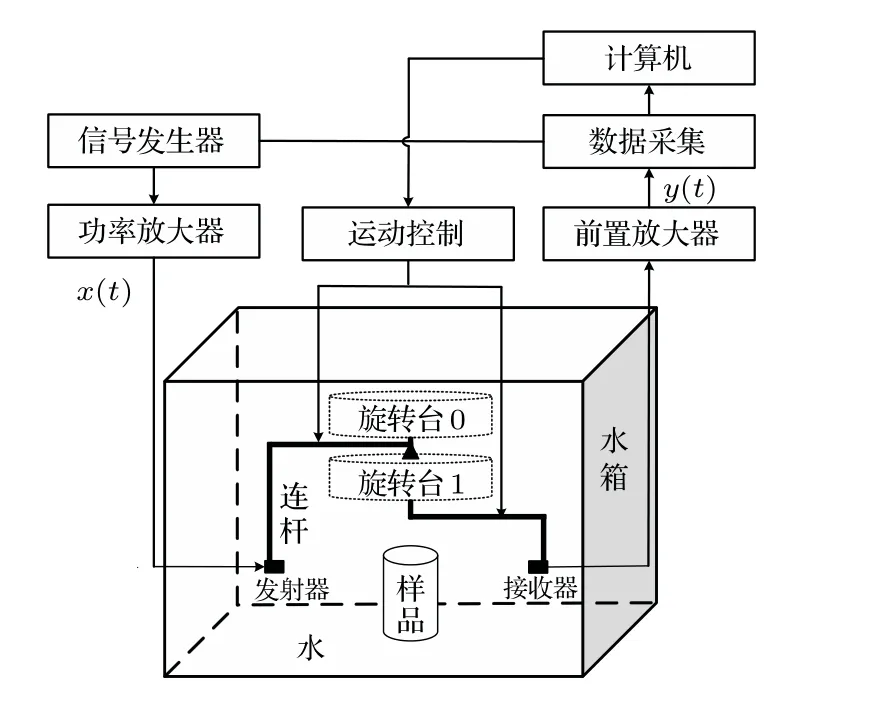
图6 实验系统示意图Fig.6 Schematic diagram of the experimental system

2.2 实验结果及分析

2.2.1 获取走时数据

为了重建样品的横断面图像，需要获得两组数据，一组为样品浸没在水中，获得相应的走时数据T0；一组为移除水箱中的样品，获得相应的走时数据T1，从而计算得到走时差数据∆T：

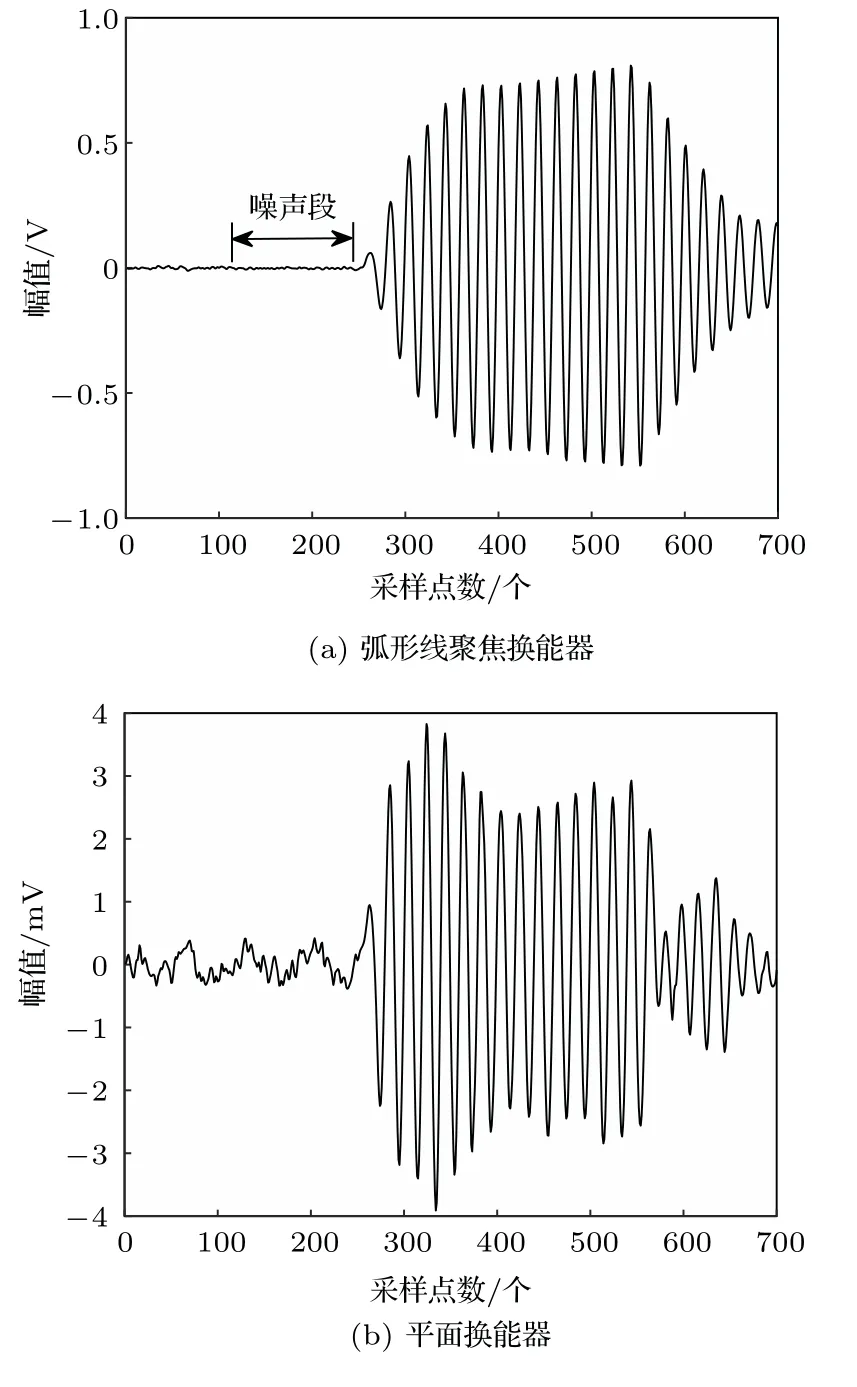
图7 聚焦与非聚焦换能器接收信号波形Fig.7 Receiving signal waveforms of focused and non-focused transducer

如图7所示，由于采用了聚焦换能器发射和接收信号，其声束聚集性能好，声能量高，声压幅值大，相较于声束无法聚焦的平面换能器，能够带来更高的信噪比，接收信号的波形质量更好。由于接收信号的信噪比较高，通过拾取直达波信号未到达之前的某一噪声段信号的最大幅值umax，并依据实际接收到的透射波形，再设定一个合适的微小增量δ，将(umax+δ)作为阈值，采用峰值检测法，拾取第一个大于该阈值的峰值点，即可轻易地获得发射信号与接收信号的第一个波峰值，对其作差便可很快获取走时数据，不仅保证了数据的精确度，而且提高了超声CT数据处理的效率。如图8所示，为采用弧形线聚焦换能器进行检测而获得的走时差数据，发射点位置代表360 个不同信号发射点的位置，接收点位置代表每一个发射点所对应的59 个不同信号接收点的位置，故可组成大小为59×360 的走时差数据矩阵。观察该数据矩阵图形可以发现，奇异点极少，说明在使用聚焦换能器获得较高信噪比的信号之后，采用上述峰值检测法来获取走时差数据较为可靠和稳定，其抗干扰性能较好。

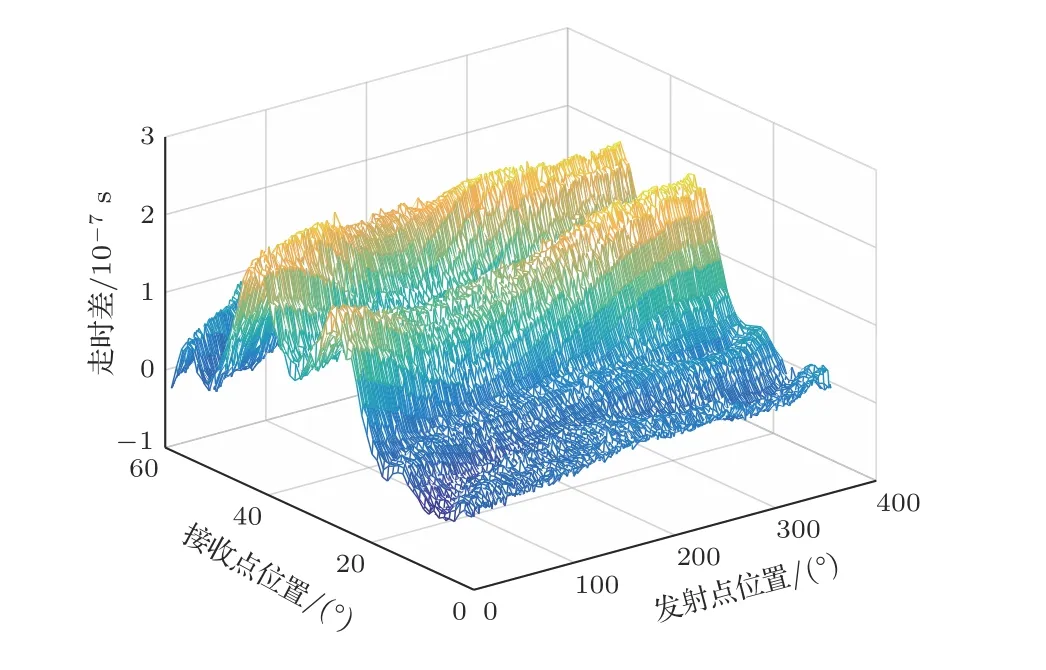
图8 走时差数据Fig.8 Travel time difference data

2.2.2 重建断层图像

关于CT 图像重建的方法主要分为两大类：一类是变换法[15]，以滤波反投影算法(FBP)为代表；另一类是迭代法[16]，以最小二乘正交分解法(LSQR)为代表。为了通过实验对比分析出两者在使用过程中的优劣，分别对图8中的走时差数据矩阵进行反向求解，重建被测样品断层的声速分布图像，归一化后如图9所示，中间箭头所指示的小黑圈表示环状笔芯的管壁，里面白色点状部分为笔芯的空洞。需要注意的是，本文在采用FBP和LSQR这两种算法进行图像重建时，是将声波传播路径视为直线形式的，而依据声波的传播特性，聚焦声束只有在均匀且各向同性的弹性介质中，才可认为是直线传播的。因此，必须保证所处于聚焦切片中被测对象的介质特性尽可能地均匀且各向同性，且声阻抗与周围其他介质尽可能相同，否则易发生散射等现象，从而影响重建结果。

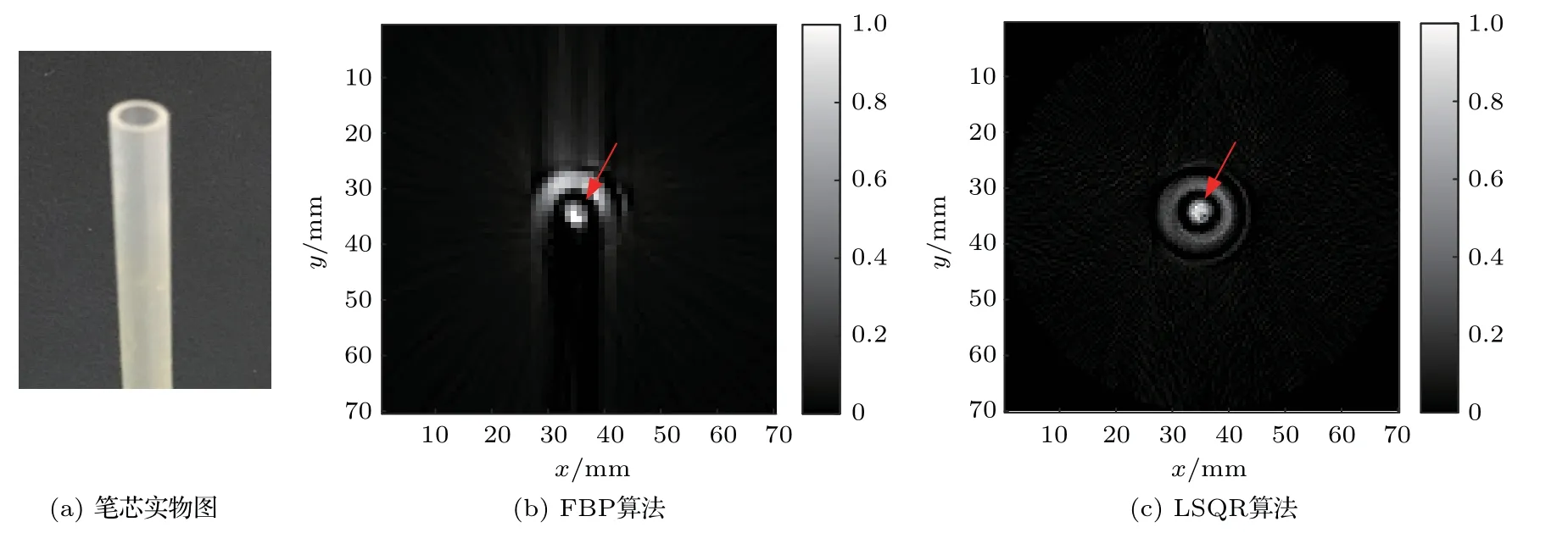
图9 图像重建结果Fig.9 Image reconstruction results

由于FBP 算法的理论依据是傅里叶中心切片定理，它对投影数据的完备性要求高[17]，即只有获得被测试样的完全投影数据后才能较好重建其断层图像，所以要保证被检样品完全被360 个扇形束所覆盖。因此，扇形束的覆盖角度θ大到可以满足覆盖条件即可。然而，换能器的声学特性限制了角度θ不能太大，如图10 所示，为实验所用弧形聚焦换能器Z轴上两倍声焦距处X轴方向上归一化后的声压分布，若最大声压值降低6 dB，对应的扇形束开角θ仅为60◦。这样，在实际放置样品时稍有偏差，就会使得部分扇形束无法覆盖整个样品，进而导致投影数据不完全，正如图11 所示，计算出的走时差数据有一小块的异常，加之该算法涉及一个滤波处理，若处理不当，很容易导致图像模糊且不完整，如图9(b)所示。

与之相反，LSQR算法克服了FBP算法的缺点，它是利用最小二乘法解决一个超定问题，并基于双对角矩阵的迭代算法和QR 分解[18]，去寻求一个最优解。主要思路是先把成像区域网格离散化，再把任意稀疏矩阵方程化为系数矩阵为方阵的方程，最后利用Lanczos 处理方法，求解方程组的最小二乘解。对于反演方程组

图10 两倍声焦距处X 轴方向上声压分布图Fig.10 Sound pressure distribution in the X-axis direction at twice the focal distance

图11 异常数据Fig.11 Abnormal data

对本文所述的超声CT检测系统而言，式(4)中的b为走时差参数，它的每个元素对应为实验所获得的走时差数据；x为慢度(速度的倒数)参数；A为系数矩阵，它的元素由每一条射线在每个网格中的长度构成，由于每一条射线只能经过某一部分网格，因此式(4)属于大型稀疏病态方程组。对此，可通过双对角化来求解式(4)，以下给出基本公式，具体的求解方式参见文献[19]。若Uk=[u1,··· ,uk] 和Vk=[v1,··· ,vk] 为正交阵，且Bk为(k+1)×k的下双角阵

运用迭代法实现矩阵A的双对角分解

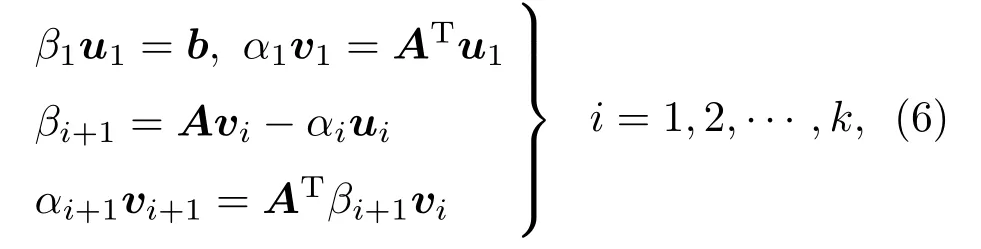
其中，eTk+1表示n阶单位矩阵的第k+ 1 行，设xk=Vkyk,rk=b −Axk,tk+1=β1e1−Bkyk，可知

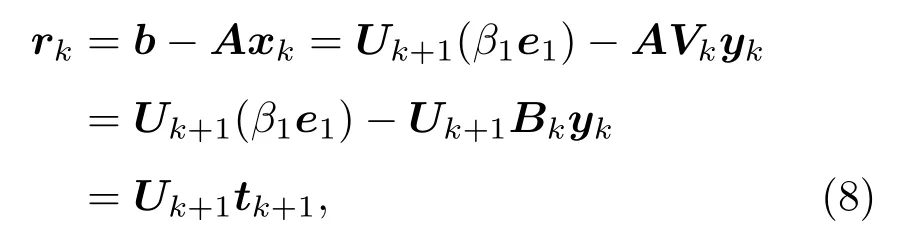
当满足给定精度时，停止迭代。由于Uk+1是正交阵，若要求∥rk∥最小，可取适当的yk使∥tk+1∥最小，解出方程组后，慢度值便可用于成像输出。由于QR 分解具有良好的稳定性，使得算法抗噪能力强，重建出的图像比较完整，清晰度也更高。图9(c)的结果表明，采用聚焦换能器并结合LSQR 算法对物体进行超声CT检测，不仅重建图像质量更佳，而且检测分辨力可达毫米量级。

在图像重建领域中，常用均方误差(Mean squared error, MSE)和峰值信噪比(Peak signal to noise ratio, PSNR)对原始图像和重建图像进行比较，来评价重建效果。MSE 主要用于比较原始图像与重建图像之间的差异程度，MSE 越小，说明重建图像越接近原始图像，而PSNR 可以对图像的质量进行评估，PSNR 越大，说明重建图像的质量越高[20]。设f(x,y)和f′(x,y)分别表示原始图像和重建图像中点(x,y)的灰度值，M和N分别表示灰度图像的长度和宽度，L为数字图像的灰度级数，则MSE表示为

PSNR表示为

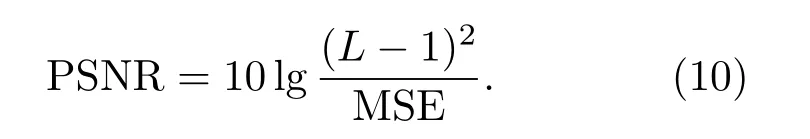
为了对比FBP算法和LSQR算法的优缺点，依据式(9)和式(10)，取L为256，分别计算使用两种算法重建图像的MSE与PSNR，同时计算出两种算法的程序运行耗时，结果如表3所示。

表3 算法对比Table3 Comparison of algorithms

由表3可以看出，与FBP算法相比，LSQR算法虽然运算时间较久，但能够重建出较高质量的图像。为了进一步对比出采用LSQR 算法重构出的图像与笔芯实际形状特征的偏差情况，取重构的二维幅值图像中−6 dB 的等高线作为笔芯的环状轮廓，如图12 中实线所示。而笔芯的实际环状边界如图12中虚线所示，对比发现吻合度较高，依据相对误差的计算公式：

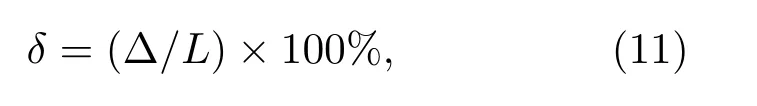
图12 重构图像与实际图像对比Fig.12 Comparison between reconstructed image and actual image

式(11)中，∆为绝对误差，L为真值。以横截面图像中外轮廓曲线为例，重构图像的外轮廓曲线近似圆形，求得平均直径为6.21 mm，计算出重构图像中外轮廓曲线的直径偏差仅为0.21 mm，相对误差为3.5%，表明利用弧形聚焦换能器并结合LSQR 算法对壁厚为1 mm的环状笔芯横断面进行CT检测，能够取得理想的成像效果，检测分辨力可达毫米级。

3 结论

本文从换能器的角度出发，分析了采用弧形线聚焦换能器作为信号发射器和接收器时，利用其焦域切片对物体进行CT 检测能够获得较高的信噪比和较精准的投影数据。同时，分析了聚焦切片大小对成像的影响，配合旋转半径为一倍声焦距的扫描机构对物体进行投影测量，不仅能够提高信噪比，为获取走时数据提供便利，提高超声CT 的检测效率，而且能够保证走时数据的精确度。通过FBP和LSQR两种图像重建算法对实验所获得走时差数据进行反向求解并成像，对比了两者的优劣。结果表明，FBP 算法计算效率高，但由于对投影数据完备性要求高，图像重建结果不理想；LSQR算法虽然计算时间较长，但是通用性好，抗噪能力强，重建出的图像质量更佳，结合适当几何尺寸的弧形线聚焦换能器进行使用，检测分辨力可达毫米量级，具有较高的工程参考价值。

为了保证被测样品能够处于聚焦切片之中，本文依据被测样品的尺寸，设计了相对应的弧形线聚焦换能器和扫描检测机构，使得成像区域的声束近似为平行声束，从实验角度研究了利用聚焦切片进行CT检测的可行性，但对于实际检测，仍需研制一种灵活多变、可适用于大多数检测对象的检测系统。此外，文中仅用了频率为1 MHz 的超声波信号对壁厚为1 mm 的环状笔芯进行了检测实验，考虑超声波在介质中传播时会发生衰减，从而降低信噪比，且衰减的强弱与信号发射频率，以及介质属性有着密切的关系，故在今后的超声透射CT技术研究中，还应当结合信号频率和被测物体声学特性进行全面研究。