棋盘洲长江公路大桥锚碇基坑施工性状数值分析

李潮

(长江大学城市建设学院，湖北 荆州 434023)

近年来，随着桥梁工程建设规模越来越大，锚碇基坑也向超大、超深的方向发展，为了深入了解锚碇基坑的受力变形性状，更好地为设计施工服务，一些学者采用数值方法对锚碇基坑开展了研究。刘化图等[1，2]介绍了武汉阳逻长江大桥南锚碇基坑内衬及支护结构的计算方法。李劭晖等[3]采用数值方法结合实测数据，总结了嵌岩地下连续墙的受力与变形特征。刘春原等[4]对不同工况下圆形地下连续墙结构内力进行了分析。王琨等[5]对珠江黄埔大桥锚碇基坑施工过程进行仿真计算，分析了圆形嵌岩地下连续墙的拱效应及开挖深度对墙体受力变形的影响。任丽芳等[6]采用三维有限元结合实测数据，分析了基坑开挖过程中的地下连续墙水平位移及坑底隆起情况。陈希等[7]、段坚堤等[8]采用有限元法模拟某双圆环形锚碇基坑开挖支护过程，认为双圆环形基坑具有明显的空间效应和拱效应。凌晓等[9]建立了有限元强度折减法评价圆形地下连续墙加内衬支护结构的安全系数。栗小祜等[10]通过有限元软件分析地下连续墙在考虑内衬收缩时的应力与位移变化情况。崔剑锋等[11]采用里兹法对圆形地下连续墙进行受力分析，并与有限元法计算结果对比，验证了里兹法的准确性。靖振帅等[12]对重庆驸马长江大桥锚碇基坑开挖施工过程进行三维模拟，分析了支护结构的应力与变形。肖景平等[13]针对岳阳洞庭湖大桥锚碇葫芦形基坑，探讨了围护结构深层水平位移、墙体钢筋应力和墙顶变形等实测值的变化规律。张军等[14]分析了降水对地下连续墙受力与变形的影响，提出增大墙体厚度可在一定范围内提高地下连续墙的自稳能力。徐江等[15]对非洲马普托大桥南侧锚碇深基坑进行模拟计算，预测了支护结构墙体的变形及周边地表沉降。

从现有文献资料看，由于深大锚碇基坑数量较少，累积的资料数据还不多，对锚碇基坑结构内力与变形研究不够充分。为此，笔者结合现场实测数据，运用数值方法对棋盘洲长江公路大桥锚碇基坑开挖及内衬施工进行全过程数值模拟，分析支护结构的受力变形及周边地表沉降变化特征，以期对类似工程的设计与施工提供参考。

1 工程概况

棋盘洲长江公路大桥项目起点位于湖北省阳新县大冶湖南岸朱唐埠村，终点位于湖北省蕲春县马家咀，南锚碇位于东湖新村居民区内。锚碇基础开挖深度为49.8m，采用内径61m，壁厚1.5m，深度59.5～64m的圆形地下连续墙加钢筋混凝土内衬进行支护，内衬从上往下依次为0～15m深、厚1m，15～30m深、厚1.5m，30～49.5m深、厚2.5m。地下连续墙嵌入中风化泥质粉砂岩深度不小于3m，嵌入微风化岩深度不小于1.5m。采用逆作法岛式开挖施工，分层开挖土体、施工内衬，内衬及土体分层厚度为3m，共有34个施工步。

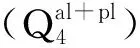
2 数值模型

2.1 计算模型

考虑到计算效率，采用平面轴对称计算模型，模型几何尺寸：水平向取5倍基坑开挖、深度200m，竖向取120m，地下连续墙深度取为61m。边界条件为侧面水平约束，底面竖向约束。墙顶标高以上土体等效为40KPa均布荷载，距离基坑开口线20m范围内施工荷载为20kPa。有限元网格以四边形为主，密度采用Single方式控制，在支护结构附近处网格划分较密，距支护结构越远，网格划分越稀疏，最小网格尺寸0.5m，最大网格尺寸8m。不同于四节点线性完全积分单元，模型采用四节点线性减缩积分单元，只在单元的中心有一个积分点[16]，如图1所示，网格划分时未出现沙漏问题。计算模型及有限元网格划分如图2所示。

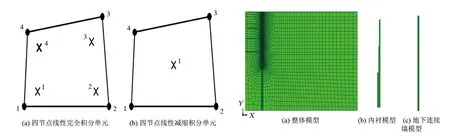
图1 单元类型 图2 计算模型

2.2 材料模型

基于勘察报告[17]所提供资料，采用总应力计算方法，材料采用Mohr-Coulomb本构模型，地层计算参数如表1所示。混凝土的c、φ值按照李云安等[18]提出的公式进行换算取值，混凝土参数如表2所示。

2.3 计算方法与步骤

1)计算方法 数值模型基于ABAQUS平台构建，采用拟静力方法，自适应时间步长，每一增量步采用隐式迭代，自动阻尼及非对称求解器，采用单元生死法模拟基坑开挖及施工内衬。

2)计算步骤 第1步为地应力平衡，第2步施加施工荷载，第3步至第36步模拟锚碇基坑开挖支护过程，依次开挖3m土体，施工3m内衬，直至开挖第17层土体，施工第17层内衬。

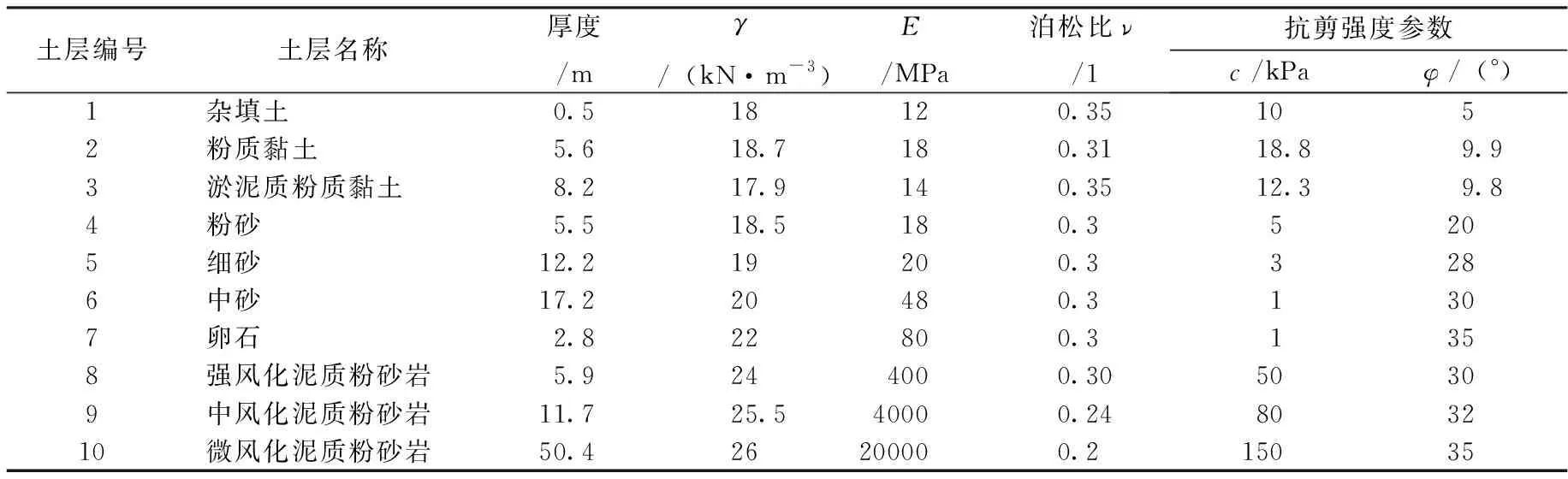
表1 地层参数

表2 混凝土参数

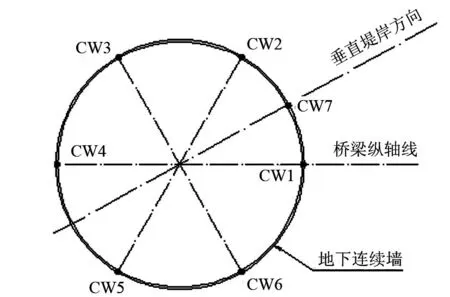
图3 地下连续墙径向位移监测点示意图

2.4 模型验证

地下连续墙径向位移监测点布置如图3所示。根据现场监测数据，监测点CW1、CW3及CW6数据未出现异常，选取其进行数值模型验证。

现场实测的锚碇基坑初始开挖及开挖完成时的地下连续墙径向位移数据与模拟结果对比曲线如图4所示。图4(a)施工工况为锚碇基坑开挖完第1层土，添加第1道内衬。图4(b)施工工况为基坑开挖至基底处，即开挖完第17层土，添加第17道内衬。由图4可知，模拟结果与实测数据符合度较好，模拟计算与监测数据对比说明数值模型较为合理，能够较好地模拟锚碇基坑开挖施工过程。

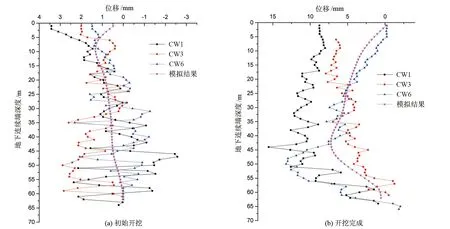
图4 地下连续墙径向位移曲线

3 计算结果分析

3.1 地下连续墙应力

地下连续墙应力曲线如图5所示，图5(a)为地下连续墙径向应力曲线，径向应力以朝向基坑内为正。由图5(a)可知，在整个施工过程中，地连墙径向应力在基坑开挖深度范围内变化较小，变化幅度为0～0.07MPa，在墙身嵌岩部分应力值增长较大。开挖至基底时，在58m处出现最大值0.81MPa。在墙身深度60.5～61m处出现径向应力反向，最大值为0.2MPa。考虑开挖造成基坑内外土压力差，导致地连墙向基坑侧偏移，而墙底由于基岩嵌固作用明显，使得墙底出现向基坑外的径向应力。

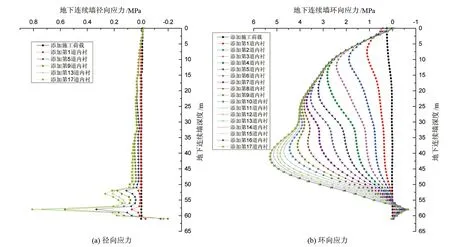
图5 地下连续墙应力曲线

图5(b)为地下连续墙环向应力曲线，环向应力以受压为正，呈现向基坑内凹形。由图5(b)可知，环向压应力最大值位置随着开挖而逐渐下移。从添加施工荷载至添加第13道内衬，即基坑开挖深度在0～39m时，最大值位于开挖面以下1～10m范围内，而添加第14～17道内衬,即基坑开挖深度在39～49.8m时，最大值位于开挖面以上1～8.5m范围内。在添加第12～17道内衬时，最大值位于41m处。在添加第16、17道内衬时，环向压应力最大值为5.3MPa。地下连续墙深度56～61m处为环向拉应力，在58m达最大值，呈V型。由于基岩的嵌固、限制作用，使得环向拉应力较小，约为墙体环向压应力的10%。

3.2 墙背土压力

地下连续墙深度范围内的墙背外侧土体压力分布曲线如图6所示。由图6可知，锚碇基坑施工全过程中，在基坑开挖深度范围内，即0～49.8m段的墙背外侧土压力很小。在嵌岩段范围内，即49.8m～61m段的墙背外侧土压力随着基坑开挖深度的增加而逐渐增大，且均为正向土压力，说明底部土体为主动土压力。在深度58m处，土压力达最大值0.85MPa。结合图5(a)，地下连续墙体径向应力最大值为0.81MPa，两者数值上基本相等。

3.3 地下连续墙径向位移

不同工况下地下连续墙径向位移曲线如图7所示。由图7可知，地下连续墙径向位移曲线的变化形态与地连墙环向应力曲线的变化形态相似，呈现向基坑内凹形。最大位移值随基坑开挖而下移，从添加施工荷载至添加第13道内衬，即基坑开挖深度在0～39m时，最大值位于开挖面以下2～13m范围内，而添加第14～17道内衬，即基坑开挖深度在39m～49.8m时，最大值位于开挖面以上1～8.5m范围内。在添加第13～17道内衬时，最大值位于41m处。在添加第17道内衬时，最大值为7.24mm，说明嵌岩圆形地下连续墙的拱效应能有效降低墙体变形。基岩嵌固作用阻止了最大水平位移的进一步下移，在整个开挖施工过程中，墙底部径向位移值较小，约为墙体最大径向位移的8%～11%，表明墙体底部基岩对墙身变形约束效果显著。

图6 墙背土压力分布曲线 图7 地下连续墙径向位移曲线

图8 地下连续墙顶部竖向位移曲线

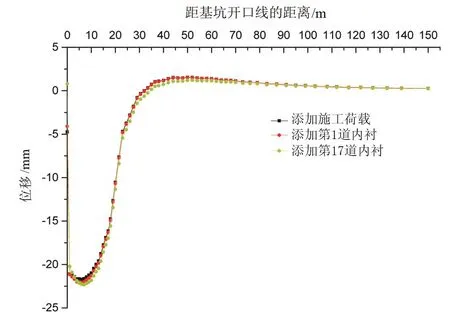
图9 周边地表沉降曲线

3.4 地下连续墙顶部竖向位移

地下连续墙顶部竖向位移曲线如图8所示。由图8可知，地下连续墙壁顶部竖向位移在整个施工过程中从0开始逐渐增大，并最终趋于稳定值7.06mm，其中从初始添加施工荷载至开挖第11层土时，增长幅度较大。墙顶变形主要发生在基坑土体开挖时；而在添加内衬时，地下连续墙壁顶部位移基本无变化。

3.5 周边地表沉降

基坑周边地表沉降分布曲线如图9所示。基坑周边地表沉降呈下凹形，地表沉降主要由施工荷载导致。而在基坑的开挖施工过程中，地表沉降变化不大，变化幅度约为0.1～0.3mm。最大沉降在距基坑6m处，为21.7mm。在距基坑开口线0～30m范围内，地表产生沉降。而在30～80m范围内，地表隆起0.1～0.15mm，主要考虑施工荷载导致周边土体挤压。根据模拟结果可知，距离基坑开口线100m范围外地表基本无沉降，基坑施工造成的影响主要在2倍开挖深度范围内。

4 结论

1)模拟结果与实测数据对比表明，在选用合适的材料参数情况下，采用基于总应力法的数值方法模拟深大锚碇基坑施工过程是可行的。

2)地下连续墙径向应力主要集中在墙身嵌岩部分，最大值0.81MPa；墙体环向应力曲线与径向位移曲线基本相似，呈内凹形，应力及位移最大值位置随开挖而逐渐下移，表现为开挖0～39m时位于开挖面以下，开挖39～49.8m时位于开挖面以上，其中环向应力以受压为主，墙底附近出现环向拉应力，约为环向压应力的10%，墙底径向位移约为墙体最大径向位移的8%～11%；施工中墙顶产生竖向位移，最大值7.06mm。

3)地下连续墙背外侧土压力主要位于嵌岩段范围内，且随开挖深度增加而增大，最大值为0.85MPa；而在开挖深度范围内墙背土压力很小。

4)周边地表沉降主要产生由施工荷载导致，最大值为21.7mm，在基坑开挖过程中沉降变化较小，在2倍开挖深度范围外，基坑开挖对地表沉降基本无影响。