基于双套站原理的雨量数据融合模型探索——以厦门市为例

肖惠珍，邱祥锋

(厦门精图信息技术有限公司，福建 厦门 363000)

由于国内外还没有做过对不同单位监测站数据进行融合的先例，因此通过大量的阅读文献和研究，参考国家双套站的原理进行雨量站数据的融合。国家级双套自动气象站在2011年1月正式进行试验运行。该试点建设工作试图通过双套自动气象站的运行来解决目前单套的自动气象站存在的一些问题，即是否能解决单套运行的自动站由于设备出现异常故障，周围环境，如雷、电等影响所造成的气象数据异常；能否在一定程度上减轻观测人员的工作量；能否在一定程度上解决目前自动气象站单套站运行存在的一些问题，预期得到更加准确、有效、稳定的观测数据及减少对应人工观测人员的工作量，从而能够逐渐实现真正意义上的监测数据的自动检测。基于双套站的工作意义与我们本次不同单位数据融合的原理和意义基本一致，因此本项目参考双套站模型，结合实际情况进行分析和融合。

1 研究方法

1.1 空间分析

根据各单位监测站点的空间分布位置及类型，根据各单位规定的各个监测点的范围，通过不同单位监测站监测范围的空间叠加分析，进而对监测站点进行划分。将提取的同名站点数据，各单位分别形成泰森多边形，将各单位的泰森多边形进行叠加，落于重叠区域的同名站点；进行地形分析：利用DEM提取山谷线和山脊线，排除位于山谷线和山脊线两边的同名点。同时利用等高线判断同名站点的地形地势在空间上是否符合融合的条件。

(1)泰森多边形分析。泰森多边形的方法在水文预报、水文分析计算和分布式水文模型中可广泛应用。泰森多边形是荷兰气候学家A·H·Thiessen提出的，是一种根据离散分布的气象站降雨量来计算平均降雨量的方法，即将所有相邻气象站连成三角形，作这些三角形各边的垂直平分线，于是每个气象站周围的若干垂直平分线便围成一个多边形。用这个多边形内所包含的一个唯一气象站的降雨强度来表示这个多边形区域内的降雨强度，并称这个多边形为泰森多边形。

(2)地形地势分析。由各个单位监测站点建设的泰森多边形进行叠加，对落入重叠部分的监测站点再进行地形地势分析，首先利用DEM提取山谷线和山脊线，排除位于山谷线和山脊线两边的同名点。同时利用等高线判断同名站点的地形地势在空间上是否符合融合的条件。

1.2 相关性分析

基于泰森多边形计算出来的同名监测站点，将同名站点的历史雨量数据作为变量，采用相关性分析同名站点之间的相关性系数。当同名站点历史雨量数据达到强相关的情况下，再进行相关系数的计算，作为雨量数据融合的权重。

关联性强的监测站距离一定很近，但距离很近的监测站关联性不一定强。因此，对于同一地点的监测站，我们通过相关系数这个具体的量化指标来判断监测站之间关联性的强弱。

(1)相关系数。相关系数是反映变量之间相关关系密切程度的统计指标。选取各单位在2016年全年的时间序列(1a)的日雨量值进行2站之间相关系数计算，通常相关系数大于0.8时，2组变量有很强的线性相关性。

(2)双累积曲线。双累积曲线是检验2个参数间关系一致性及其变化的常用方法。选取各个单位2016年历史雨量数据中，每间隔1h时段的雨量值进行双累积曲线分析，拟合结果如图1所示。

图1 监测站点双累积曲线拟合示例

拟合结果表明，各单位同名雨量监测站点之间相关系数高的雨量站之间双累积曲线形态一般较好。

(3)关联站。每个雨量站选取相关系数高、双累积曲线形态较好的雨量站为其关联站。根据相关性分析结果，各个同名站点之间相关性都很高，双累积曲线也十分吻合，因此，对于同名站点可进行雨量数据的融合。

2 差异数据融合规则

数据融合目的是从多源的各个有效数据中，排查出有可能存在故障或精度不高的数据，用比较准确的数据，按照既定的规则，产生标准的、格式一致的、经得起考验的、服务于共享的防汛监测数据。

数据整合时，需要对地点接近或相同、类型相同的有效监测数据，按照预设的规则和权重，对各数据进行加权平均，产生对某一标准地点的权威监测数据。

2.1 异常值系数

2个同名站点只存在1个缺失值的情况，3个同名站点存在1个缺失值、2个缺失值的情况。异常值系数计算模型如下：

(1)

(2)

2.2 确定融合规则

(1)2个站点融合规则。1个缺失值，1个有效值的情况则直接用该有效值;2个有效值，且2个有效值的异常系数都小于0.3，则根据2个有效值权重计算。2个有效值，且其中1个有效值的异常系数大于0.3，则剔除该组数据。2个有效值，且2个有效值的异常系数大于0.3，则剔除该组数据。

(2)3个站点融合规则。2个缺失值，只有1个有效值的情况则直接用该有效值;1个缺失值，只有2个有效值，且2个有效值的异常系数都小于0.3，则根据2个有效值权重计算。1个缺失值，只有2个有效值，且一个有效值的异常系数大于0.3，则剔除该组数据。1个缺失值，只有2个有效值，且2个有效值的异常系数都大于0.3，则剔除该组数据。3个有效值，其中3个有效值异常系数都小于0.3，则分别用各站点的权重参与融合计算；3个有效值，但其中2个同名站点的异常系数小于0.3，一个大于0.3，则用异常值小于0.3的2个雨量站的权重进行融合；3个有效值，但其中只有1个有效值的异常系数小于0.3，则剔除该组数据。3个有效值，且3个有效值的异常系数都大于0.3，则剔除该组数据。

2.3 权重计算

2.3.12个有效值权重计算-均方差法

标准差(StandardDeviation)，也称均方差(mean squareerror)，是各数据偏离平均数距离的平均数，标准差能反映一个数据集的离散程度。通常，某个指标的标准差越大，表明指标值的变异程度越大，提供的信息量越大，在综合评价中所起的作用越大，其权重也越大。相反，某个指标的标准差越小，表明指标值的变异程度越小，提供的信息量越小，在综合评价中所起的作用越小其权重也应越小。

具体计算步骤如下：

Ai为A站点的第i个雨量值，Bi为B站点的第i个雨量值，其中i=1，2，3…，n。

平均值

(3)

(4)

标准差

(5)

(6)

权重

(7)

(8)

计算结果见表1和表3。

2.3.23个有效值权重计算-主成分估计

主成分估计(principal component estimate)是Massy在1965年提出的，它是回归系数参数的一种线性有偏估计(biased estimate)，同其它有偏估计，是为了克服最小二乘(LS)估计在设计阵病态(即存在多重共线性)时表现出的不稳定性而提出的。主成分估计采用的方法是将原来的回归自变量变换到另一组变量，即主成分，然后用最小二乘法对选取主成分后的模型参数进行估计，最后再变换回原来的模型求出参数的估计。详见表2。

3 融合数据使用

3.1 监测站点加密

Delaunay三角网的构建也称为不规则三角网的构建，就是由离散数据点构建三角网，如图，即确定哪3个数据点构成一个三角形，也称为自动联接三角网。即对于平面上n个离散点，其平面坐标为(xi，yi)，i=1，2，…，n，将其中相近的三点构成最佳三角形，使每个离散点都成为三角形的顶点。

三角网格加密方法是：内部点是在三角形的中心内插点，以最近的几个点为依据根据距离越近贡献越大的原则确定边缘上的点。

表1 2个有效值权重

表2 3个有效值权重

表3 2个有效值权重

3.2 克里金差值

克里金法提供了一个在有限区域内对空间变量进行无偏最优估计的方法。Borga和Vizzaccaro用线性函数作为普通克里金插值的变异函数和复二次函数曲面拟合的插值方法进行降水插值比较，发现普通克里金法的插值精度较好。

普通克里金(Ordinary Kriging)提供了一个在有限区域内对空间变量进行无偏最优估计的方法，是根据样本空间位置不同、样本间相关程度不同，对每个样品赋予了不同的权重，进行滑动加权平均，以估计待测点的值。

(9)

式中，Z*(x0)—待测点估算值；Z(xi)—第i个样本点的实测值；n—参与计算的实测样本个数；λi—第i个样本点的权重系数。

而权重是根据克里金插值的无偏估计和方差的最小得到。公式如下：

(10)

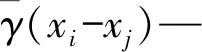
3.3 融合站点的差值成果

将进行加密后的监测站点作为克里金差值的方法将离散的测站点差值成连续的区域雨量分布情况，利用ArcGIS的GP服务构建模型，完成差值、裁剪、生成雨量等值线等操作后，得到融合后的雨量值与其他离散雨量站差值的全市雨量分布情况图，如图2所示。用历史雨量值进行验证，该模型的计算成果与实际情况基本符合。若监测值明显存在异常，可通过系统交互界面选择参与模型计算的监测站，再进一步生成全市雨量等值线分布图。

4 结论

本文通过双雨量站原理结合加密差值的模型算法计算出来的融合数据和原始的观测数据进行校验，等值面与实际区域面基本吻合，但仍存在着差异，需要在更多历史雨量数据的验证过程中不断修正该模型，最终能够得到更权威的融合数据模型，此类输出数据的融合算法需要考虑得更加全面。本文评估算法的思路对雨量监测数据的融合质量评估有一定的借鉴意义。