几何入门阶段习题讲评的教学思考与建议——从一道七上模考几何填空题讲评说起

☉江苏省清江中学 张绍俊

最近在七年级上册期末复习阶段，一份模考卷上的一道几何填空题得分率很低，笔者本来准备让几个做出答案的学生上台示范一下他们的解法，没有想到连续几个学生虽然获得解答，但是解法都显现出不够优化的情况，这让笔者即时调整了教学进度，把这节课多数时间花在该题的解题教学进程上.本文给出这道习题的讲评手记，并跟进几何习题讲评的相关思考与教学建议，供研讨.

一、一道几何习题的讲评手记

考题：以∠AOB的顶点O为端点引射线OP，使∠AOP∶∠BOP=3∶2，若∠AOB=17°，则∠AOP的度数为______.

阅卷记录：这道填空题全班只有20%的学生填出正确答案（10.2°，51°）.

讲评预设：考虑到正确率很低，需要多花一些时间进行讲评.为了追求更好的讲评效果，决定先安排一位填出正确解答的学生上台讲解他的思路，然后让学生互相学习、交流.

讲评记录：先让获得正确解答的几个学生站起来，让其他学生学习，站起来的几个学生都很有自信，然后安排学生小Y上台讲解他的思路，他写出两个算式，如下：

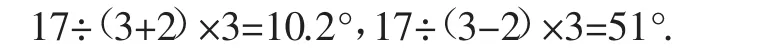
教师追问下面的学生是否看懂了，那几个正确的学生表示都能理解，但其余的学生仍然表示不太理解.于是教师示意其他学生上台来构造图形，更直观形象地解释这两个度数，于是学生小J上台后在黑板上经过调整得到如下两个图形（如图1、图2）：

图1

图2

在两个图形的启发之下，有一半左右的学生表示能理解.接下来是教师跟进讲评.

教师讲评：学生小Y的两个算式是典型的“小学解法”，而学生小J的图形分析更加直观形象，但是仍然有不足，主要缺陷是图形不精准，我们应该学会会构造更加精确的图形，我们应该先画出相对精准的∠AOB=17°，然后分析射线OP的可能位置，教师接下来示范相对精准的构图（如图3、图4）.

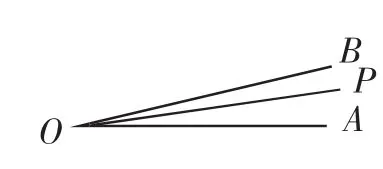
图3

图4

有了相对精准的图形分析之后，接下来可以引入方程工具，在图3中，分别设∠AOP=3x，∠BOP=2x，可得2x+3x=17°，解得x=3.4°，于是∠AOP=3x=10.2°；

在图4中，分别设∠AOP=3y，∠BOP=2y，可得3y-2y=17°，解得y=17°，于是∠AOP=3y=51°.

综上，∠AOP=10.2°或51°.

经过上述分析，多数学生都能理解并整理出详细过程，但是我们的讲评仍然在继续.

解后回顾：同学们虽然觉得这道题较难，但它有一个类似的或者说相同结构的线段习题.

同类习题：已知线段AB=17cm，在直线AB上有一点P，且满足AP∶BP=3∶2，求AP的长.

学生很快得出如下解法，先画出图形，然后分析两个可能的点P的位置（如图5），并且分类讨论得出AP的长为10.2cm或51cm.

图5

回到考题：受到线段图形“两图合一”的影响，我们也可将图3、图4“合二为一”，得出图6.

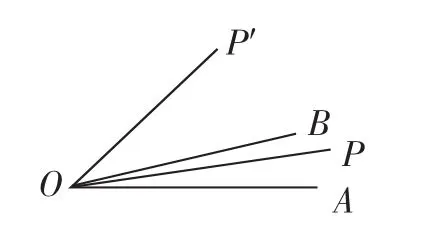
图6

讲评效果：讲到这儿，再了解学生对该题的理解与掌握时，大家都表示已经彻底想通了，于是教师再让学生分小组对这道习题进行改编，自主提出问题并解决，通过学情反馈（变式再练了一道同类题，这里限于篇幅，略去），学生解这类问题的正确率达到82%.

二、几何入门阶段习题教学的思考与建议

1.习题讲评要从答案核对走向解法探究

在习题量很大的课堂中，常常是答案核对式的讲评为主，这类讲评的效果非常低下，往往是会的学生会，不会的学生只是满足于记录答案，但并没有机会深入思考、究错与理解.只有当一节课中待讲评的习题真正降下来、减下来，才可能有时间从答案核对式的讲评走向解法探究式的讲评.探究解法需要时间，需要学生先有独立思考，然后经历小组议论、全班展示、教师评析等全过程，有时对学生并不完整、有漏洞的思路或过程，教师还要引导学生参与优化，直到解题思路完全贯通.

2.几何入门阶段需要训练精准作图能力

平面几何是很多学生进入初中阶段学习成绩的一个重要分水岭，有些代数适应性好的优秀学生往往也会对平面几何问题敬而远之.以笔者的教学经验来看，不少平面几何适应性不好的学生，对于精准图形的构造常常掌握得不好.比如，上文中学生小J对于17°的大小偏差太大，原因是学生大脑中对于一些特殊角度的适应不好，比如90°、60°、45°、30°，这些特殊角度要通过必要的练习能徒手画出它们的大致大小，这样在遇到类似17°这样的角度时，就可利用45°与30°的差来近似构造出17°角，从而为后续研究提供一个相对精准的平台.试想，如果像小J构造的图4一样，则求出一个角度为51°后会发现与图4中∠AOP为钝角是矛盾的，会对解题方向造成偏差，不利于快速解题.特别是，作为入门阶段的几何教学，需要特别重视精准作图能力的训练，当学生能对图形有相对精准的理解之后，对于后续几何学习十分有利，比如，等腰三角形的形状、全等三角形的变换研究、不同形状的直角三角形，等等，都需要精准作图的基本功.

3.习题讲评要重视“让学”与“究错”

精心准备习题讲评素材之后，需要认真预设讲评的组织过程，特别是重视“让学”与“究错”环节的设计.这里的“让学”最主要的方式就是让学生上台讲解，暴露他们的思路与过程，这样就可引导其他学生参与分析，学习其中的合理成分，并纠正其中的不足与错漏.这样不仅讲题的学生能有收益，其他学生也能在这个互动、对话、究错过程中学习提升.我们见到的很多课堂，常常是教师自己讲，一讲到底，不给学生上台讲解的机会，当然也看不到学生的错误，但这种“掩而盗铃”式教师一讲到底，学生的错误也就多出现在限时独立考试过程中，教师在学生考试之后感叹：“我讲了多少遍，你们怎么还不会？”只有我们平时上课讲题时充分放手，让学生上台讲题、展示，让一些错漏、稚嫩、不严谨的解法与思路多多显现出来，教师跟进评析、示范与优化，这样的教学是精准指导，一定可以促进学生切实提高解题能力.

4.讲评后要有“多解归一”的结构揭示

波利亚在名著《怎样解题》中对解题之后的回顾反思提出了深刻的指导意见，罗增儒教授对波利亚的解题教学理论做出了“中国解读”与教学推广，在很多一线教师中产生广泛的影响.比如，习题讲评之后需要有解后反思的教学阶段，具体来说，像上文教学片段中，最后链接讲评了线段问题，并将两种可能的图形“合二为一”，实现了“多解归一”的结构揭示.事实上，数学解题教学中，很多老师重视的往往是一题多解，对于解法的不断探究也是一些教学研讨QQ群的热闹话题，这类研究风气作为教师的个人兴趣无可厚非，但是如果过分偏重于一题多解并积极向学生宣传自己研究到的一题多解，而缺少必要的优化、简化，则是不恰当的，因为追求“更初等的解法”或者“回到定义去解题”这种解题观点应该通过我们的教学向学生传递与渗透，往往站得更高，就能看得更全面、更深入，也就能理解多种解法的“殊途何以同归”，从而引导学生通过做一题、会一类达到通一片.

三、写在后面

教学即研究.不只是公开课教学、示范课学习、教研组评课等教研活动才需要或值得开展研究，日常教学活动中，我们每天都走进课堂，这是教研活动的“第一现场”，像华东师大李政涛教授所指出的，要十分重视“第一现场”中我们的“现场学习力”的提升.上面提供的教学手记是近期课堂的一次真实场景，笔者的记录还不是很完整，表达也不够形象生动，观点阐释也以个性化表达居多，期待同行的批评与指正.