薄膜型声学超材料的管道消声特性研究

刘继宾，吕海峰，王普浩，姬艳露

(中北大学机械工程学院，山西 太原 030051)

0 引 言

噪声严重影响人们的正常生活，干扰仪器和设备的正常运行，并且严重降低武器装备的作战性能和隐身性能。由于军事装备向着更加高速、隐身性能要求更加严格的方向发展，轻量级结构和紧凑空间噪声防护的设计至关重要[1]。

近年来，声学超材料尤其是薄膜型声学超材料成为声学研究的热点。2008年，YANG等[2]制作了薄膜型声学超材料，在圆形弹性薄膜上固定质量块，并将薄膜固定在骨架上，在低频范围内实现有效隔声，并且厚度低于毫米级，实现了轻质低频。2010年，南加州大学NAIFY等[3]在薄膜上粘结一个圆环，提高了超材料的传递损失量，增加了带隙宽度。2012年，香港科技大学梅军等[4]在弹性薄膜上粘结两块半圆形金属片，制作了暗声学超材料，这样的结构具有多重共振，可以实现低频宽带的几乎百分百吸收。兰州大学TIAN H等[5]对带环形结构的薄膜声学超材料进行了数学模型和分析方法的研究，通过改变环形质量块的位置和数量来改变声学超材料的性质。西安交通大学MA F Y等[6]对比了多种形状的质量块对于带隙结构的影响，在频率为100 Hz以内获得了超低频弯曲波带隙，并提出了共振模态的群体理论。

总体来说，声学超材料在在低频隔声、低频吸声、低频减振领域的超越性能，为低频减振降噪技术开辟了一条新的途径。但声学超材料主要是通过隔声来进行噪声控制，在实际管道消声时需要有气流通过，并且传统的消声器安装体积较大，不适合紧凑型设计。

本文设计了一种薄膜型声学超材料的管道消声装置，研究了影响声学超材料性能的控制因素。通过理论计算了薄膜的特征频率，通过仿真和实验研究装置的传递损失来反映声学超材料在低频范围内的声学性能，并进一步研究改变其结构参数对消声性能的影响。

1 理论分析

薄膜型声学超材料是由四周固定的弹性薄膜中心附着质量块组成的，为研究薄膜型声学超材料的消声机理，将声学超材料安装在管道壁面，如图1所示。

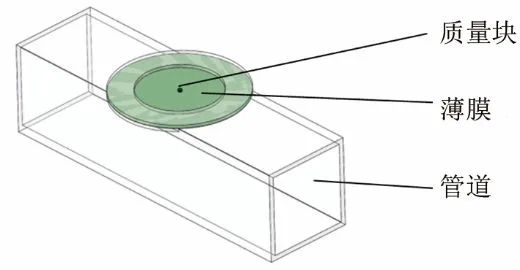
图1 研究声学超材料消声性能的装置Fig.1 The device for studying the noise elimination performace of acoustic metamaterial

1.1 薄膜振动方程

当薄膜受到外力时，就会发生变形，然后在张力T作用下产生振动[7]。

图2 不同坐标系统中薄膜面元的示意图Fig.2 The schematic diagrams of membrane surface element in (a)rectangular coordinates; (b)polar coordinates

假设一弹性薄膜半径为a，面密度为σ，受到的张力为T，在管道入射声波的作用下，弹性薄膜表面产生的声压为

其中，pa为声压振幅，ω为声波的圆频率，那么在dxdy的薄膜面元上受到的外力为

因此，作用在整个面元上的总力为

式中，η为薄膜上一点在垂直方向上的位移。

根据牛顿第二定律得到面元的运动方程：

将求解坐标由直角坐标转换为极坐标，r为离圆心的径向距离，θ为r与极轴的夹角。则x=rcosθ，y=rsinθ，由于薄膜为圆形对称振动，则振动与θ无关。整理可得薄膜的强迫振动方程为

其中：

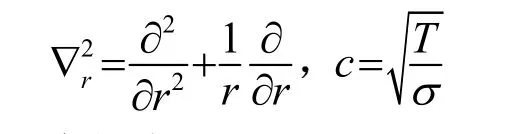
令解为

代入方程(5)可得对于径向变量r的方程为

式中，k为声波波数。

式(7)为二阶非齐次常微分方程。该方程的解一般包括一个特解Q1和一个通解Q2。观察式(7)，当取Q1为常数，可得特解为

因此，方程的一般解可表示为

式中，A为常数，J0为零阶柱贝塞尔函数。

将式(9)代入式(6)，可得薄膜在声压作用下的位移表达式为

利用边界条件，在r=a处有η(r=a)=0，代入式(10)便可定得

由此得

薄膜在声压的作用下，平均位移振幅为

其中，J2(ka)为二阶柱贝塞尔函数。

可得薄膜特征频率为

式中，µmn(µ10=2.4048,µ11=3.8317,µ12=5.1356,µ20=5.5201⋅⋅⋅)为柱贝塞尔函数的一系列根值。

1.2 薄膜振动的等效集中参数

当薄膜振动时，在同一时刻，不同径向位置的位移是不均匀的，因此可以采用等效集中参数的方法，将薄膜的振动等效为圆心一点的振动。

假设把薄膜的振动等效为圆心处有一个等效的集中质量Me在等效集中弹簧Ke作用下振动，那么对于集中参数系统，振动的特征频率可以表示为

当在圆心处附加一个质量块Mm时，等效总质量变为Me+Mm，则得到系统的特征频率

当在薄膜中心附加质量时，整个薄膜系统的特征频率减小。

2 超材料声学性能影响因素分析

2.1 有限元模型建立

采用COMSOL软件声固耦合模块对圆形弹性薄膜进行消声特性分析研究。图3为将消声装置模型导入COMSOL后的网格划分示意图。模型为截面积50 mm×50 mm，长度200 mm的长方形管道,管道侧壁上装有圆形弹性薄膜，薄膜半径为25 mm，厚度为0.2 mm，预应力为4 N·m-1，边缘固定约束，薄膜的密度为1 300 kg·m-3，杨氏模量和泊松比分别为7×105Pa和0.49。与管道内空气和外界大气形成声固耦合边界。定义管道的一端为入口，另一端为出口，进行频域分析，求得传递损失。

图3 COMSOL有限元仿真模型Fig.3 The COMSOL finite element simulation model

2.2 仿真结果与分析

2.2.1 超材料的声学性能

图4 消声装置的传递损失曲线Fig.4 Transmission loss curve of silencer device

图5 传递损失5个峰值频率处的薄膜位移云图Fig.5 Membrane displacement nephograms at five peak frequencies of transmission loss

图4所示为该装置的传递损失曲线图。可以看出在0～700 Hz范围内，该装置在频率为60、135、215、300、380 Hz处出现了5个传递损失峰值。图5为各个峰值频率处对应的薄膜位移云图，各阶振型均为中心对称振动，最大振幅位于薄膜圆心处。由式(14)可得，圆形弹性薄膜的前五阶共振频率为60.05、137.84、216.09、294.40、372.81 Hz，由此可知，薄膜的共振频率即为其消声工作频率，当入射声波频率与薄膜的共振频率相同时，系统发生共振，声能转换为薄膜的动能，传递损失达到最大，此时消声效果最好。薄膜的传递损失与其振幅有关，薄膜的振幅越大，传递损失值越高。薄膜在第一阶共振频率处振幅最大，传递损失峰值达到了最大，为54.53 dB。

2.2.2 预应力对超材料声学性能的影响

薄膜的共振频率与预应力以及面密度有关，面密度又与薄膜的厚度有关。当薄膜厚度为0.2 mm时，改变加载在薄膜上的预应力，观察其对传递损失的影响，如图6所示。图6中预应力分别取4、20、37 N·m-1。

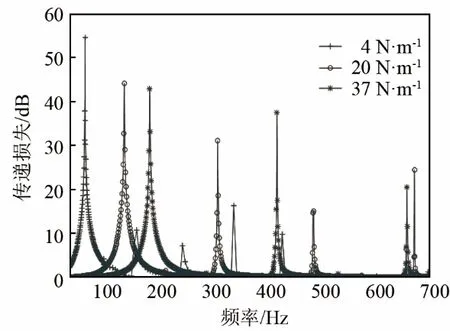
图6 薄膜预应力对传递损失的影响Fig.6 The influence of membrane prestress on transmission loss

从图6可以看出，当随着预应力的增加，该装置的传递损失峰值频率整体向高频偏移。由式(14)可知，薄膜的特征频率，当预应力增加时，系统刚度增加，从而使得系统的共振频率增加，传递损失峰值频率随之往高频偏移。在预应力为4 N·m-1时，薄膜的第一阶频率处振幅最大，传递损失最高。

2.2.3 面密度对超材料声学性能的影响

保持预应力为37 N·m-1不变，改变薄膜的厚度，从而改变薄膜的面密度，图7为薄膜厚度分别取0.2、0.4、0.6 mm时的传递损失曲线。

由图7可知，当薄膜厚度增加时，面密度增大，薄膜的特征频率降低，系统的传递损失峰值频率整体向低频偏移。

2.2.4 附着质量块对超材料声学性能的影响

在厚度为0.2 mm，预应力为37 N·m-1的薄膜圆心处增加半径为2 mm的质量块，得到不同质量的质量块下的传递损失曲线，如图8所示。

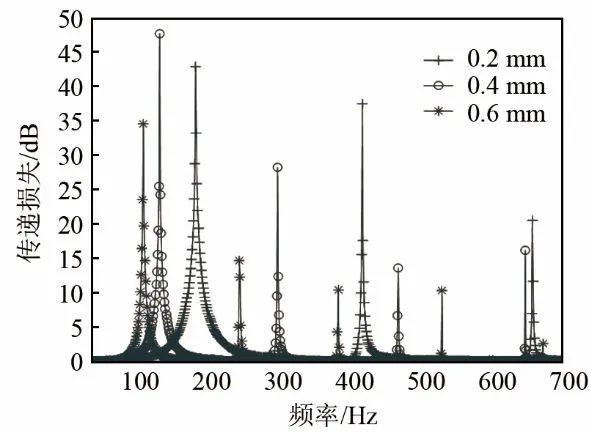
图7 薄膜厚度对传递损失的影响Fig.7 The influence of membrane thickness on transmission loss

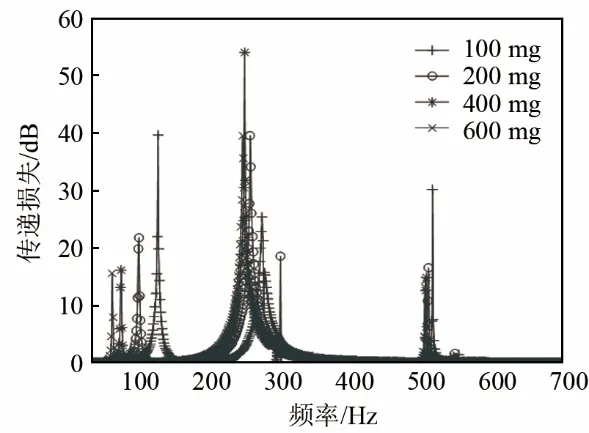
图8 附加不同质量块的传递损失曲线Fig.8 The transmission loss curves for different attached mass blocks

从图8中可以看出，随着质量块质量的增加，第一阶频率降低，对应的传递损失也随之减小，由式(16)可知，等效质量的增加导致系统的共振频率减小，所以第一阶频率向低频偏移；第二阶和第三阶频率基本无变化。薄膜在质量块为400 mg时，第二阶频率处的振幅最大，传递损失达到了54 dB。从图9薄膜剖面在各阶峰值频率处的位移云图可以看出，在第一阶频率处，主要是薄膜中心的质量块振动，因此，质量块质量的改变对一阶峰值频率有较大的影响；在第二、三阶频率处，主要是质量块周围的薄膜振动，而质量块静止，因此质量的改变对于系统的消声峰值频率基本无影响。

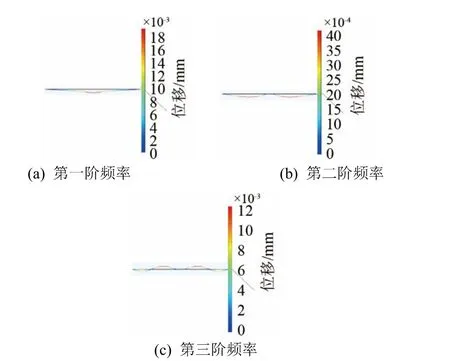
图9 传递损失峰值频率处薄膜剖面位移云图Fig.9 Membrane displacement nephograms at the peak frequencies of transmission loss

3 超材料声学性能测试

3.1 传递损失测量原理

本实验采用声学超材料系统的传递损失来验证消声效果。传递损失测量选用双负载法，其测量原理如图10所示：声源扬声器发出的平面波A向下游传播，遇到消声器时有一部分B被反射回来，另一部分透过消声器，这样消声器下游有前进波C和反射波D。利用阻抗管中的四支传声器测量得到的声压进行运算得到消声装置的传递损失值。

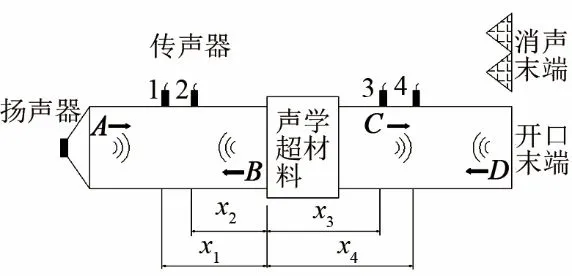
图10 传递损失测试原理图Fig.10 Schematic diagram of testing transmission loss

3.2 超材料制作与实验平台搭建

利用匀胶机(图11(a))制作实验所需薄膜，按照100 : 3的比例将硅胶与固化剂混合，利用匀胶机的离心力制备厚度分别为0.2、0.4、0.6 mm的薄膜，薄膜样品如图11(b)所示。

图11 薄膜制作Fig.11 Membrane preparation (a)spin coater;(b)membrane sample

将制作的薄膜通过两块外径为80 mm、内径为50 mm的刚性板，夹持安装在截面积50 mm×50 mm、长度为200 mm、侧壁开有直径为50 mm孔的长方形管道上，组成消声装置，并将消声装置放入实验平台中，研究其消声性能。

测试装置如图12所示，传递损失测量系统主要由功率放大器、扬声器、传声管道、AWA14425型ICP(IEPE)传感器、NI USB-DAQ9234四通道IEPE数据采集卡、Lab-VIEW采集系统等组成。将采集到的信号进行处理得到消声系统的传递损失曲线。测试中声音信号采用正弦信号，频率范围为30～700 Hz，步长为10 Hz。

图12 消声性能测试实验平台Fig.12 Experimental platform for testing noise elimination performance

3.3 实验结果

3.3.1 薄膜预应力对传递损失的影响

图13为薄膜厚度为0.2 mm，预应力分别为4、20、37 N·m-1时，实验测得的消声装置的传递损失曲线(实线)和仿真的传递损失曲线(虚线)。

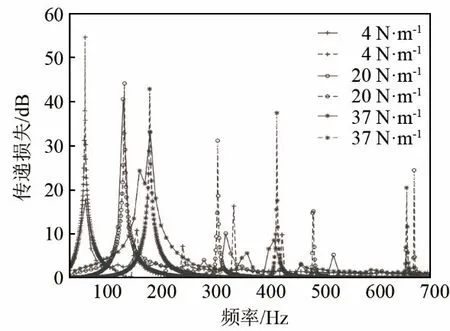
图13 薄膜预应力对传递损失的影响Fig.13 The effect of membrane prestress on transmission loss

从图13中可以看出，实验结果与仿真结果基本保持一致。随着预应力的增加，系统刚度增加，消声装置的传递损失峰值频率向高频偏移，当预应力由4 N·m-1增加为37 N·m-1时，第一阶频率偏移了120 Hz。

3.3.2 薄膜厚度对传递损失的影响

图14为保持预应力为37 N·m-1，分别取薄膜厚度为0.2、0.4、0.6 mm时的实验结果。

薄膜厚度的增加导致面密度的增加，超材料的共振频率随之降低，往低频偏移了110 Hz。

3.3.3 附着质量对传递损失的影响

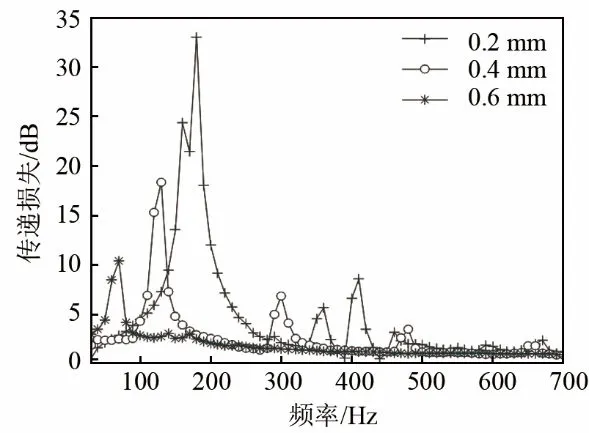
图14 薄膜厚度对传递损失的影响Fig.14 The effect of membrane thickness on transmission loss

图15是不同质量块对传递损失的影响结果图。通过硅橡胶将质量块固定在薄膜中心，薄膜保持预应力为37 N·m-1，厚度为0.2 mm，研究质量块分别为100、200、400、600 mg时对装置消声性能的影响。

由图15可知，增加质量块，且随着质量块质量的增加,第一阶频率向低频偏移，共偏移了50 Hz，并且实现了100 Hz及以下超低频消声，第二和第三阶频率基本无影响。

图15 不同质量块对传递损失的影响Fig.15 The effect of attached mass blocks on transmission loss

实验结果与仿真存在误差的主要原因是由于薄膜样品制作时的工艺误差以及实验环境对实验结果的影响。

4 结 论

本文首先从理论分析了薄膜的振动特性，接着通过仿真和实验研究了薄膜型声学超材料的声学性能，得出结论如下：

(1)薄膜在低频范围内具有良好的消声性能，其消声工作频率为薄膜的共振频率，且薄膜振幅对于传递损失有重要影响，薄膜的振幅越大，传递损失值越高。

(2)通过增加施加在薄膜上的预应力可以使消声峰值频率往高频偏移，当薄膜预应力由4 N·m-1增加为37 N·m-1时，频率偏移了120 Hz。

(3)增加薄膜厚度可以使频率往低频偏移， 当薄膜厚度由0.2 mm变为0.6 mm时，频率共偏移了110 Hz。

(4)在薄膜上添加质量块实现了100 Hz及以下超低频范围内的消声，并且随着质量块质量的增加，第一阶峰值频率往低频偏移，但第二三阶频率无影响。

本文的研究将为主动声学超材料以及紧凑型管道消声器的设计提供依据。