基于BPSO-KNN算法的被动声呐目标分类识别技术研究

朱宗斌，陶剑锋，葛辉良，郑 佳

(中国船舶重工集团公司第七一五研究所，浙江 杭州 310023)

0 引 言

声呐是海军进行水下作战的重要装备，而声呐目标分类识别技术则是声呐装备的关键技术之一。目前较常用的目标分类识别算法主要有反向传播(Back Propagation,BP)神经网络、支持向量机(Support Vector Machine,SVM)、k最近邻(k-Nearest Neighbor,KNN)分类等[1-2]。其中，最近邻分类算法由于算法简单、容易理解和实现且分类效果较好，因此广泛应用于目标分类识别中[3]。被动声呐主要依据探测到的目标辐射噪声进行海上目标分类识别，然而由于海洋环境复杂和水声信道特殊，如何在舰船辐射噪声中提取有效的特征一直是声呐目标识别的研究重点和难点。目前使用较多的特征提取方法有：时域特征提取、线谱特征提取、双谱特征提取等[4-7]。在舰船辐射噪声中螺旋桨节拍对舰船的辐射噪声存在明显的振幅调制，这种幅度调制信号携带着舰船的重要特征信息，这些特征信息能够用来进行目标的分类识别。对舰船辐射噪声求功率谱即可得到目标功率谱特征，功率谱特征包括线谱特征和连续谱特征，这两种特征广泛应用于声呐目标的分类和识别中[4,6-9]。

鉴于水中舰艇目标低频特征丰富，本研究基于提取得到的低频功率谱谱线特征直接用于被动声呐目标识别，但是由于直接提取得到的特征量维度过高，导致特征间相关性较大，不利于分类器的识别。特征选择是一种基于对建模数据分类时提供最强预测能力特征子集的方法，有效的特征选择方法可以降低特征空间的维度，提高对样本集的正确识别率和识别效率。基于对自然界鸟群捕食行为的模拟，KENNEDY等[10]在1995年提出了粒子群优化(Particle Swarm Optimization,PSO)搜索算法，在PSO中，每个粒子都有一个候选解，候选解的好坏由粒子所在位置对应的适应度值(fitness value)表示，粒子通过在空间中不断运动，利用粒子的适应度函数值逐渐搜索到最优位置，即找到较优的候选解。本文基于二进制粒子群优化(Binary Particle Swarm Optimization,BPSO)算法结合KNN算法实现对功率谱特征的优化选择和k最近邻(k-Nearest Neighbor,KNN)算法中k参数的优化处理，并将算法优化后的特征向量和参数输入至KNN分类器中，实现对被动声呐目标的分类识别。利用本文算法对4类实际海上目标进行分类，验证了该算法具有较好的特征优化选择能力和被动声呐目标分类识别能力。

1 BPSO算法原理

PSO提出之初，较多应用于解决连续空间优化问题[11]。它首先随机初始化一群独立粒子，粒子群中每个粒子的属性由其具有的速度和位置两个特征表示，速度特征即该粒子在迭代过程中需要移动的位移，位置特征表示粒子候选解的值，粒子在迭代过程中使得初始粒子的速度和位置不断变化，粒子位置的优劣程度由适应度函数衡量。根据计算的适应度函数，粒子通过寻找个体极值最优解Pibest和全局极值最优解Pgbest不断更新位置。设在D维空间中有N个粒子构成的粒子群，第i个粒子在D维解空间的速度和位置分别表示为vid=(vi1,vi2,⋅⋅viD)，xid=(xi1,xi2,⋅⋅xiD)，其中，i=1,2,⋅⋅,N，其搜索的个体最优位置和全局最优位置记为pid=(pi1,pi2,⋅⋅piD)，pg=(pg1,pg2,⋅⋅pgD)，则粒子群算法的速度和位置更新公式可表达为

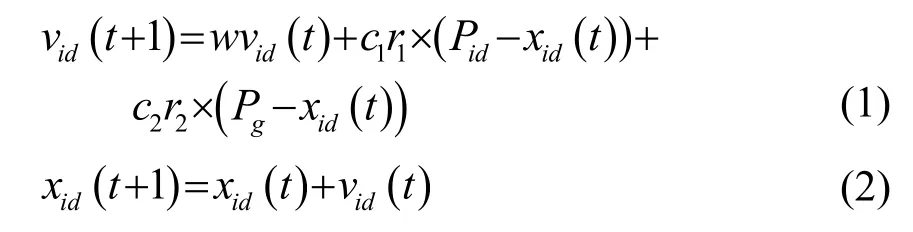
式(1)中：w为惯性系数，表示前次经历速度对当前速度的影响程度；c1和c2是学习因子，均为非负常数，可以反映粒子群间的信息共享和交互；r1和r2为分布在[0,1]区间的随机值。

由于PSO算法主要应用于连续空间的优化，1997年Kennedy等[12]提出了针对离散问题的二进制粒子群优化(BPSO)算法。在BPSO中，粒子的速度和位置均是从概率的角度来定义的，粒子群中每一个粒子的位置都被限定为0或1，0或1位置的选择由粒子速度来决定，粒子速度的变化大小决定了粒子位置的翻转概率，粒子速度一般利用sigmoid函数限定在[0,1]区间内，则BPSO位置更新公式为

式(3)中，r为范围在[0,1]区间的随机数。

在BPSO算法求解中，c1和c2两个学习因子影响着个体粒子和整个粒子群之间的信息交互。若c1比较大，粒子对个体信息较为重视，粒子在更新时会更多地向个体极值最优解Pibest学习，粒子的全局搜索能力较强；若c2值比较大，粒子的更新更容易受到全局极值最优解Pgbest影响，粒子局部搜索能力增强，因而容易较早陷入局部收敛。针对此种情况，RATNAWEERA等[13]提出一种学习因子改进调整方法，即c1在算法过程中，由初始的较大值逐渐调整为较小值，而c2则由初始的较小值调整为后期的较大值。c1、c2在整个迭代过程中的变化可表示为

式中，c1b和c1e分别表示c1的初始值和最终值，c2b和c2e分别表示c2的初始值和最终值，i和M分别表示当前迭代次数和最大迭代次数。

2 BPSO-KNN算法设计

2.1 粒子设计

本文算法中，每个粒子的结构由参数k和特征掩码两部分构成，其中参数k即KNN算法中的k参数，即该样本通过距离其最近的k个样本数据来对其属性进行判断，特征掩码是一组二进制组合，表示该特征选中与否。粒子设计形式如表1所示。

表1 BPSO-KNN算法粒子设计Table 1 Swarm design of BPSO-KNN algorithm

表1中，前面nk位代表参数k，其十进制值的表达可利用下式进行转换：

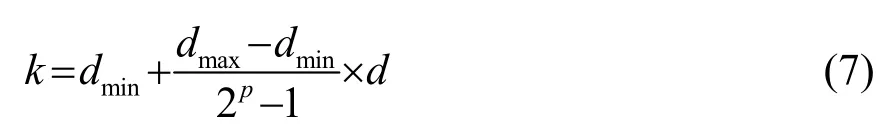
式中，dmin表示k参数的最小值，dmax表示k参数的最大值，p和d分别表示二进制位组合的长度以及该组合代表的十进制值，根据需要可对参数的精度和范围进行设定。余下nF位表示特征掩码，1和0分别代表该特征被选择和未被选择，因此，不同的特征组合即对应不同的二进制组合。

2.2 适应度函数设计

适应度函数是衡量粒子构成优劣的重要标准，本文中适应度函数值的大小由两部分内容决定，即KNN分类算法的正确分类率和被选中特征的数量，一般来说，一个粒子较低的特征维度和较高的分类正确率所对应的适应度函数值较为理想，因此，本文BPSO-KNN算法中的适应度函数值可表达为

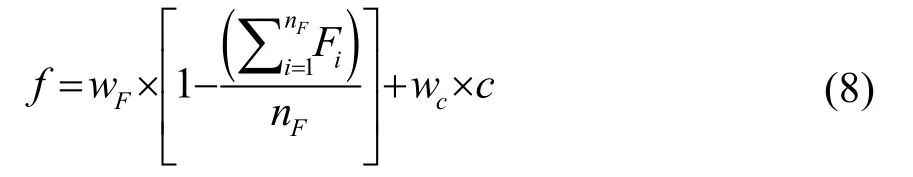
式中，wF和wc分别表示所用特征个数的权重和KNN对测试样本集分类正确率的权重，Fi代表特征位串对应的值，即0或者1。

2.3 算法流程

BPSO-KNN算法流程图如图1所示，算法步骤如下：

(1)粒子群初始化，包括确定粒子群个数、算法迭代次数、粒子速度范围、粒子群各参数等。

(2)根据粒子结构将每个粒子的二进制表达表征为BPSO-KNN的参数k和特征子集。

(3)对样本集目标进行KNN分类，计算粒子群中各粒子适应度值，选出并更新粒子个体极值最优值Pibest和全局极值最优值Pgbest。

(4)判断算法结束条件，本文即判断是否达到最大迭代次数，如果达到最大迭代次数则输出结果并结束，则此时全局最优位置即参数k和特征组合最优状态，输出内容主要包括参数k、最优特征组合和测试样本集正确分类率。若未达到最大迭代次数，则继续进行步骤(5)迭代计算。

(5)继续迭代计算，根据公式(1)、(3)更新粒子的速度和位置，同时根据公式(5)、(6)调整学习因子c1和c2。并返回步骤(2)继续算法过程。

3 实验分析

3.1 目标辐射噪声功率谱特征提取

舰船辐射噪声由线谱和连续谱组成，若舰船噪声随机过程用{S(t)}表示，则船舶噪声周期性局部平稳过程模型[14]可表示为

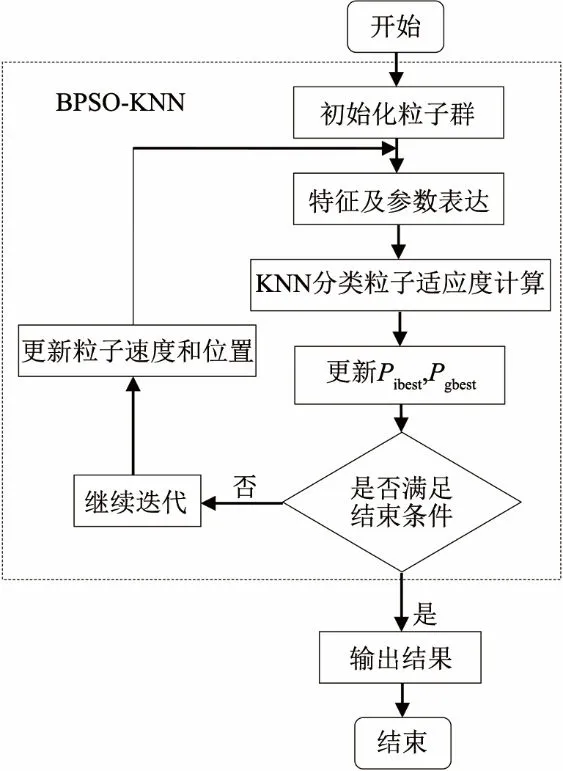
图1 算法流程图Fig.1 Flowchart of the BPSO-KNN algorithm

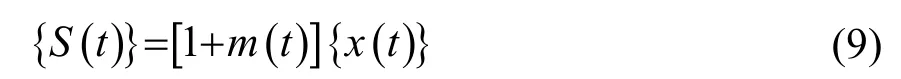
式中，x(t)表示窄带平稳白色高斯随机过程，m(t)表示调制函数，是慢变化周期信号，S(t)为周期性局部平稳高斯随机过程。

舰船辐射噪声功率谱可用下式表达为

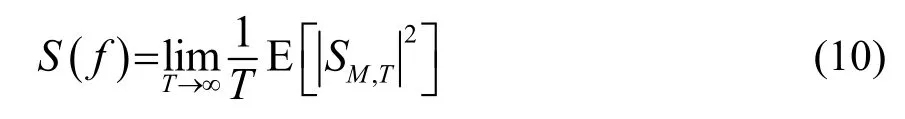
式中，T是傅里叶变换时每段截取的信号长度，M为该信号段对应编号，E是集合求平均。式(10)是舰船辐射噪声谱在数学模型下较为严格的定义，该过程需要截取无穷多个信号段，并且每段截取的信号长度都趋于无穷。在实际应用中，往往只能作有限长信号的集合平均。在利用目标的功率谱谱线特征进行目标识别时，较高的频率分辨率有利于目标识别，但是考虑到实际的物理特征和应用需求，本文目标的时域单波束数据采样率Fs=5 000 Hz，傅里叶变换点数取4 096，即频率分辨率Δf≈1.22 Hz。选取被动声呐目标功率谱特征区间为[5,90]Hz，由于本文直接将区间内的功率谱作为特征向量，因此共得到70维特征向量。

由于直接求得的功率谱特征各目标的可比性较差，因此首先对样本集各维功率谱特征进行预处理。预处理包括特征归一化和野值去除两个步骤。

本文均是提取得到的功率谱特征，特征量纲相同，考虑到后续继续加入其它量纲不一致并且差别较大的特征，若对每个样本进行所有特征归一化，就会导致较大数值的特征掩盖掉较小数值特征的变化，此时进行分类，较小特征的变化可能被忽略掉，不利于分类器的识别，因而本文采取对各维功率谱特征分别进行归一化预处理。

本文采取的预处理公式为

式中，x表示直接求得的功率谱特征量，x*表示归一化后的特征量，min(x)表示该特征量的最小值，max(x)表示该特征量的最大值。m和σ分别表示对式(11)归一化后的特征量x*求均值和求均方差处理，xnew表示预处理后的特征量。

3.2 实 验

随机选取4类海上被动声呐目标共7 776个样本数据，其中目标1为水下目标，其它3类为水面舰船目标，每类目标各1 944个样本，对于目标时域单波束数据，选取0.819 2 s时间长度信号作为单个样本原始数据，对选取的时间长度数据求取功率谱特征，对每个样本目标提取得到的功率谱特征都首先利用式(11)、(12)进行特征预处理。随机选取5 832个样本作为KNN分类器的训练数据，余下1 944个样本作为分类器的测试数据用来验证本文算法的有效性。4类目标在训练数据和测试数据中所占个数如表2中所示。

对训练样本集和测试样本集进行70维特征处理，得到的均值和均方差值如图2所示。

图2中，分别给出了训练样本集和测试样本集的均值和均方差值，其中横坐标表示频率维度，纵坐标表示数值幅度。

随机挑选4个不同种类的目标样本，按照式(11)、(12)特征预处理后的70维功率谱特征谱线如图3所示。

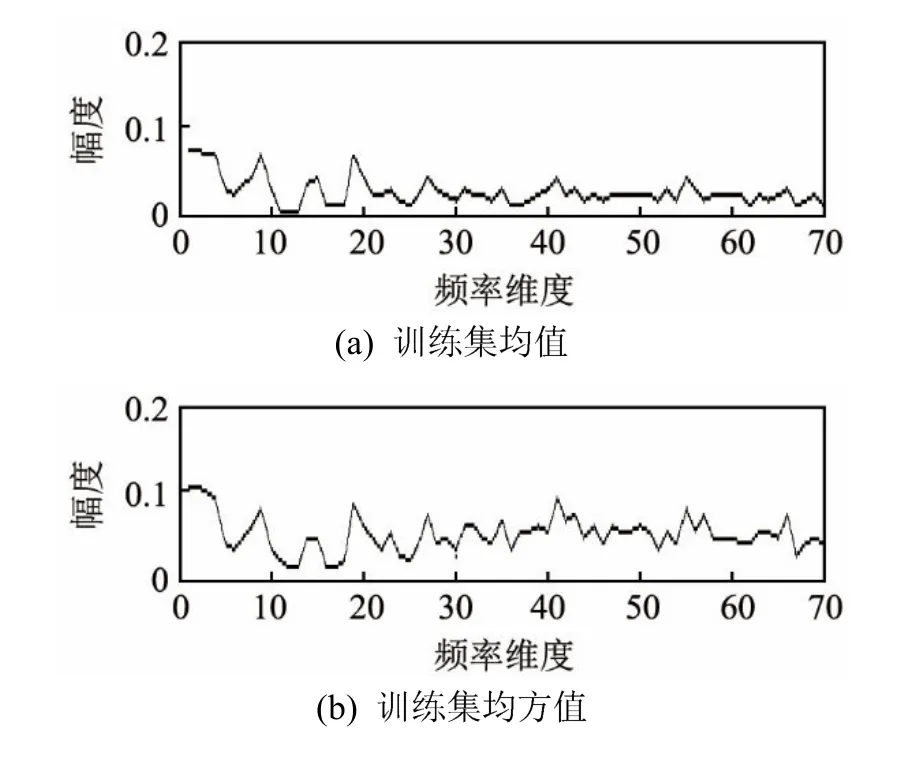
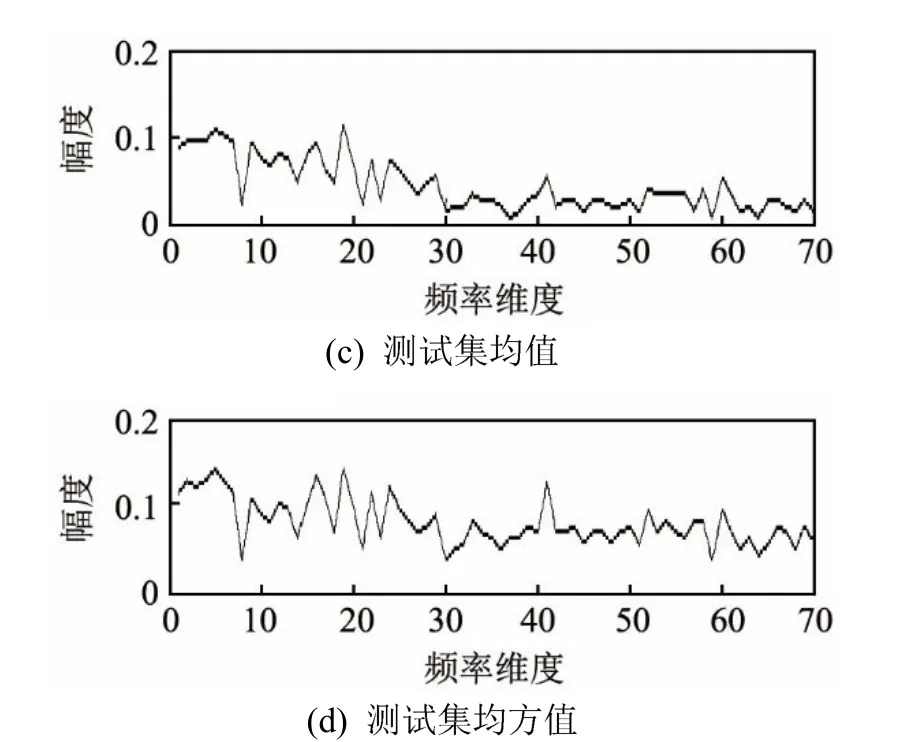
图2 样本集均值和均方差值Fig.2 Mean value and standard deviation value of sample set

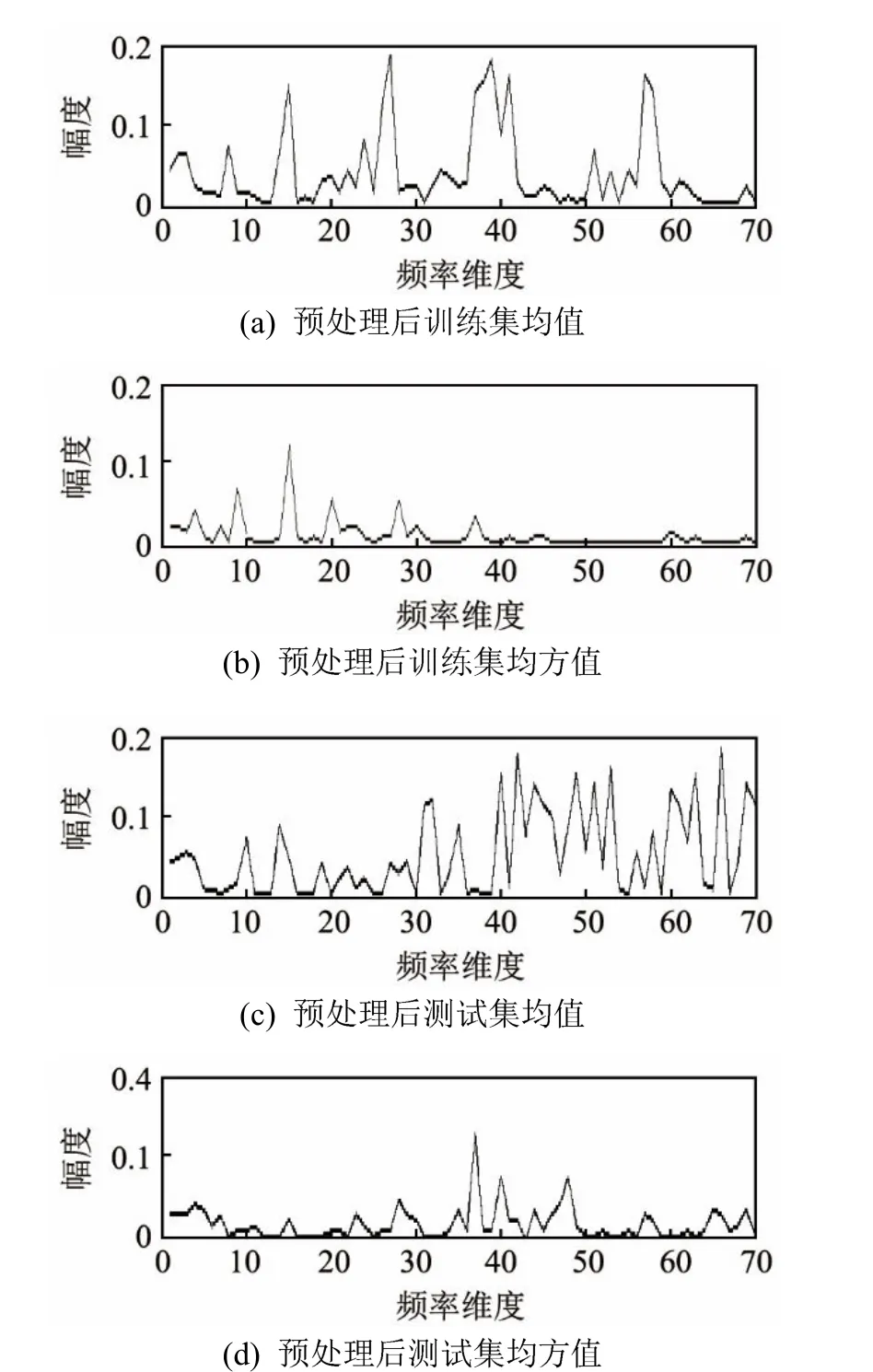
图3 预处理后的功率谱特征谱线Fig.3 Power spectral characteristics after preprocessing

结合多次实验结果，BPSO-KNN算法中各参数设置如下：粒子群个数取30，算法最大迭代次数M=20，参数k的位串个数nk=20，特征量位串个数nF=70，即算法解空间维数D=90，粒子速度初始范围取[-5,5]，惯性权值w=1，若c1、c2均取固定值，则算法容易陷入局部收敛导致分类器的正确识别率降低，故式(5)、(6)中的c1b=2.75，c1e=1.25，c2b=0.5，c2e=2.25，通过对c1、c2的调整进而实现对粒子速度的调节，防止算法陷入局部收敛，式(8)中权值wF=0.2，wc=0.8，KNN分类算法中k∈[1,100]。最近邻分类器采用欧氏距离(Euclidean distance)作为距离衡量，分类器的正确识别率由式(13)表示：

式中，n表示对该类别目标正确分类的个数，N表示该类别目标的总个数。

直接利用KNN分类算法和本文算法分类的结果对比如表2所示。

表2中，KNN算法识别所用特征个数为原始功率谱特征70个，参数k取推荐值1，BPSO-KNN算法中经过特征选择后所用特征个数为24个，算法优化后参数值k=21。由表2结果可以看出，在大幅优化特征维度的情况下，本文算法对4类声呐目标的正确识别率分别较KNN算法提高了23.51%，9.72%，3.02%，1.14%；对4个目标的总正确识别率BPSO-KNN算法较KNN算法提高了8.60%。并且不难看出，直接利用KNN算法进行分类识别时，对4个不同目标的识别能力差别较大；而本文所提算法对各个目标的识别能力相当。因此，BPSOKNN不仅大幅优化了特征向量，提高了目标分类识别效率，而且增加了对各个目标的正确识别率，验证了本文算法在被动声呐目标识别上的有效性。

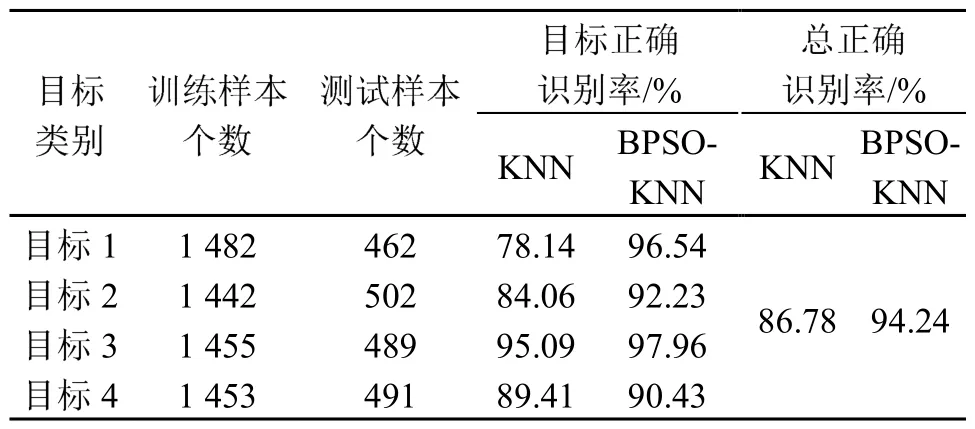
表2 KNN算法与BPSO-KNN算法分类结果对比Table 2 Comparison of recognition results between KNN and BPSO-KNN algorithm

4 结 论

本文提出一种基于二进制粒子群优化(BPSO)算法和最近邻(KNN)分类算法相结合的BPSO-KNN算法，实现对被动声呐目标功率谱特征的降维优化处理。该算法将分类器参数和特征量粒子化，通过粒子群的不断变化来对KNN参数进行优化和搜寻较优的特征组合。实验表明，BPSOKNN算法可对KNN进行参数优化和对功率谱特征进行降维优化处理，提高对目标的分类识别率。该算法对被动声呐目标的自动识别分类有参考价值。