改进型轴向永磁调速器的优化设计

吴 迪，关焕新，邱力伟，郭祎珅，杨 柏，赵柏翔

（沈阳工程学院 a.研究生部；b.新能源学院，辽宁 沈阳 110136）

永磁调速器（adjustable permanent magnet coupler，APMC）作为新型的非接触式的调速和传动的装置，主要应用在电动机和负载之间，其工作原理是通过永磁转子的磁场与导体铜转子上形成的涡流场之间的耦合效应传递转矩，它能够消除电机轴与负载轴之间的刚性联接，这样就能够很好地解决在传动过程中产生的振动和损耗，能最大化地提高转矩的传递效率和降低由于传动过程而造成的谐波污染。作为一种新型的传动和调速装置，其能够非常广泛地应用在大型旋转设备与电动机之间，起到无级调速或减速的可调速的耦合系统作用，图1为轴向永磁调速器的装置结构图。

对轴向APMC的永磁转子进行改进和优化设计，采用空间粒子群的优化算法对永磁转子形状进行优化，主要优化的参数包括铜盘厚、磁极个数、极弧系数、切割高度和切割角度，同时对多优化目标进行设计和优化计算，建立优化后的永磁调速器模型并进行求解，获得最优解。通过Ansoft软件对优化后的永磁调速器进行仿真分析，可以看出优化后的永磁调速器的性能得到了很大程度上的提高，验证了所提出的优化方法的有效性。

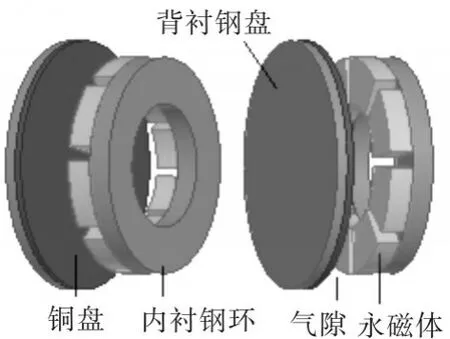
图1 轴向永磁调速器结构

1 改进型永磁调速器及优化问题的提出

通过对轴向永磁调速器中的永磁转子的结构进行改进，以达到提高永磁调速器的运行性能的目的，并建立了基于改进后的轴向永磁调速器参数范围的优化问题的数学模型。

1.1 永磁转子的改进

常规的永磁体转子为瓦片型磁极，其气隙通常含有大量的谐波，这对永磁调速器的性能造成了极大的负面影响。文献［1］已经证明了采用弧形表面转子能够有效地减少气隙谐波含量，从而可以更好地提高APMC的应用性能，但是考虑到弧形表面转子工艺复杂并且成本较高，因此提出使用梯形转子代替弧形转子，图2为改进永磁转子结构。在图2中，h代表梯形表面切割高度，θ代表切割角度。

图2 改进永磁转子结构

1.2 优化数学模型的建立

尽管已经确定了轴向APMC的基本物理模型，仍然还需要对每个结构的参数数值进行精确选择，因为其取值对永磁调速器的应用方面有很大的影响，所以在参数的优化设计上也进行了详细地分析计算。需要优化的参数主要有铜盘厚度（t）、磁极个数（n）、极弧系数（α）、切割高度（h）、切割角度（θ）、气隙磁密（kBδ）。轴向永磁调速器的其他参数为固定值，表1为改进后的轴向永磁调速器参数范围。

表1 永磁调速器参数范围表

根据表1建立改进型轴向永磁调速器目标函数及约束条件方程如下：

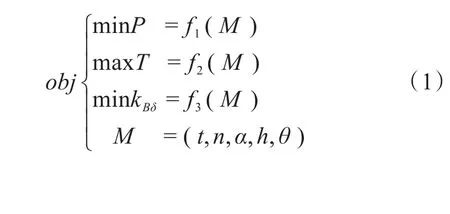
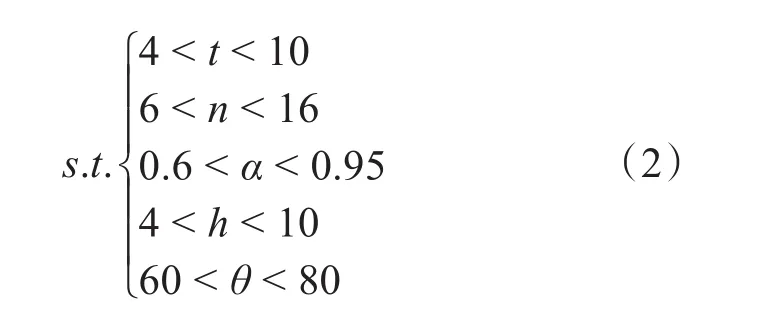
2 基于BP神经网络预测模型的建立

BP神经网络模型主要应用于模式识别中的非线性映射和分类等问题的处理。二十世纪后期，Robert Hecht Nielsen证实并得出对于任何在闭区间的一个连续的函数均可以通过隐层的BP网络来逼近，因而一个3层的BP网络可以完成任意的n维到m维的非线性映射，作为一种多层前馈网络，BP网络可以有效地对误差进行预测。在BP网络中产生的误差会迅速的反向传播，为了最大化地减小误差的产生，需要对每层中的连接权值进行反复的缩小，图3为优化的网络拓扑结构图。

图3 优化网络拓扑结构

2.1 BP神经网络的算法

下面为BP神经网络算法步骤：

1）结构参数和定义。

定义训练样本个数为N，确定输入变量为Mi=[ ]

t,n,α,h,θ(i=1,2,…,N)，N为总样本的数量。

经过n次迭代后，对神经网路的数值进行输出，分别为

对神经网络的n次迭代后的期望值进行设定：

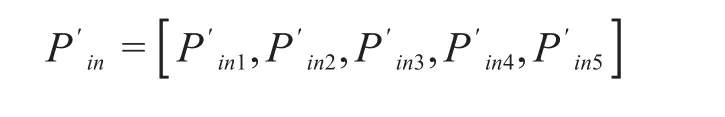
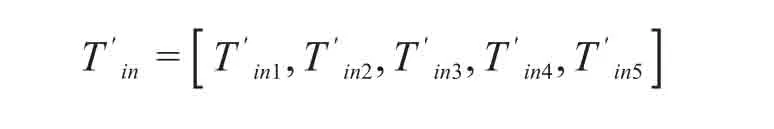
同样需要定义误差精度为e。

2）对两个权值ωij、ωjε进行赋值，保证其为极小的非零值。

ωij(i=1,2,3,4,5,j=1,2,3,…,Ψ)为迭代到第n次后在隐层和输出层连接权的权值；Ψ为隐层神经元个数；ωjε(j=1,…,Ψ,ε=1,2)为迭代到第 n次时，隐层与输出层连接权的权值。

3）输入值为Mi，需要令n=0。

4）当正向传播时，只要将训练样Mi作为输入，可以得出神经网络的输出为Pkn、Tkn，经计算获得与期望值P′kn、T′kn之间的误差为E(n)，计算公式为

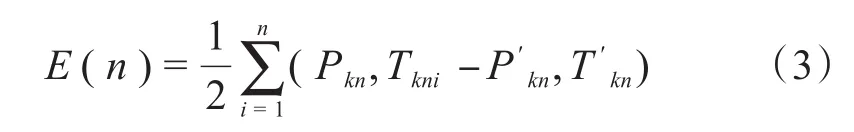
对式（3）进行计算，误差为网络输出值和期望值的差，需要对其进行如下处理：

①若E(n)＞e，继续到步骤5）；

②若E(n)≤e，直接转到步骤6）即可。

5）反向传播（误差修正）。

反向传播环节也叫作误差修正环节或者权值最优搜索环节，权值的修正梯度为误差对权值的偏微分权值修正方法如下［2］：

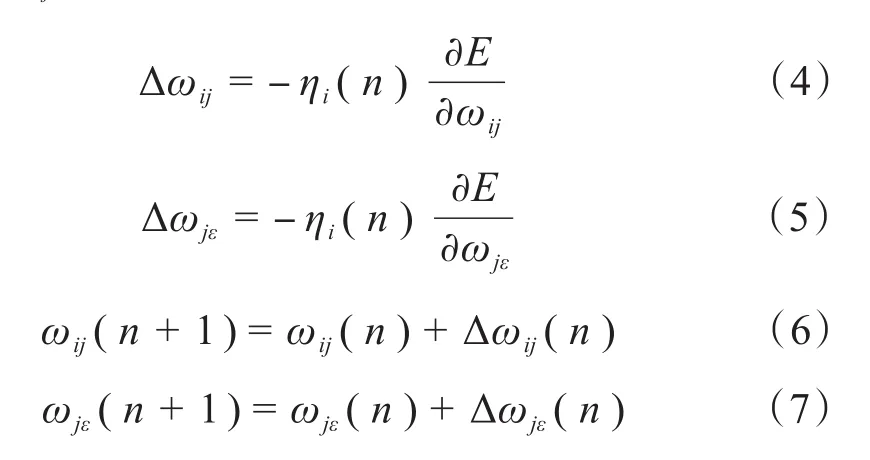
其中，ωij(n)表示网络的连接权符号（ωij(n)是多个权值的集合而不是单一的权值）；ηi(n)表示网络的学习效率，其选取方法如下：

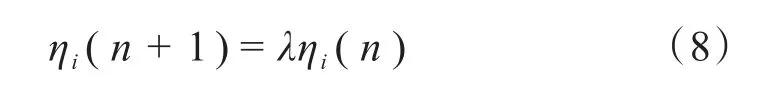
其中，λ的取值遵循以下规则：

①E(n)＞E(n+1)时，λ∈（1.2，1.6）；

②E(n)＜E(n+1)时，λ∈（0.2，0.6）。

新的参数计算完成后带入步骤3）继续循环，直至达到指定误差精度e。

6）算法终止。

2.2 性能预测

1）确定网络结构

在确定了永磁体的形状之后，还需要对各结构的参数进行确定。为了能够更加直观的对轴向永磁调速器进行性能分析，可以对轴向APMC进行设定，设定其为输入空间的集合，所以这些待设计参数的性能指标可以设为输出的空间集合。神经网络的输入层包括铜盘厚度（t）、磁极个数（n）、极弧系数（α）、切割高度（h）、切割角度（θ）、气隙磁密（kBδ）；输出层的空间集合包括P和T。可以看出输入层神经元数目为6，输出层神经元数目为2。隐含层神经元数是通过文献［2］提出的试凑法来确定的，通过效率对比确定了隐含层神经元数为30个，所以神经网络结构为6-30-2。BP输入层以及隐含层的传递函数为tansig函数，输出层的传递函数为purelin函数。

2）网络模型的建立

仿真预测过程中的网络模型的建立同样至关重要，需要合理的选择函数，对训练数据进行归一化处理，此次仿真选用的函数为premnmx函数，将训练数据带入premnmx函数中进行仿真，仿真的数据选择采取tramnmx进行相同预测处理，premnmx函数主要应用在最后数据的反归一化的处理中。建立BP网络，运用工具箱中的trainlm函数，其对应的算法选择Levenberg-Marquardt。在BP网络的训练设置中，通常可以设置训练次数为200，学习效率为0.05，网络的目标误差为0.01。

表2为部分神经网络的训练样本，其仿真结果是通过Ansoft3D有限元仿真软件进行模拟所得出的数据。

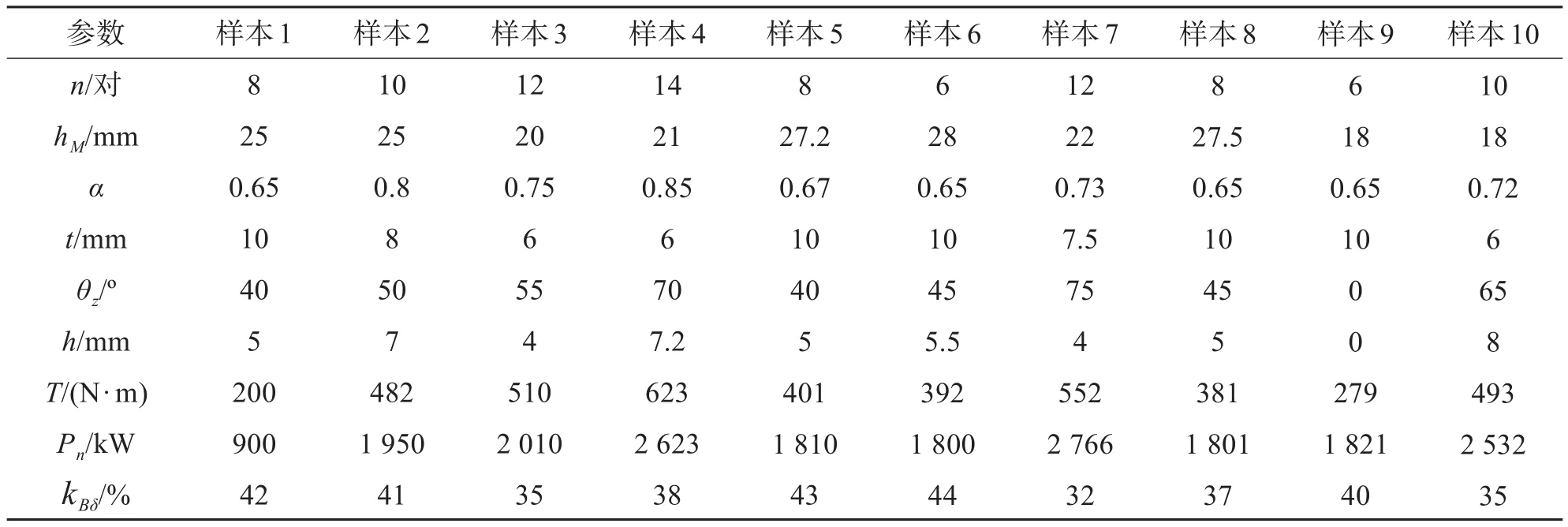
表2 神经网络训练样本

3）预测结果分析

2.1节中的步骤2）中已经完成对网络的训练，采用sim验证函数对训练结束的网络进行仿真验证，sim函数采用的主要验证方式需要训练样本集合外的数据作为测试空间集合，对其进行选取来进行测试。表3为网络测试数据和相应性能测试的实验值和预测值中有代表性的一部分。

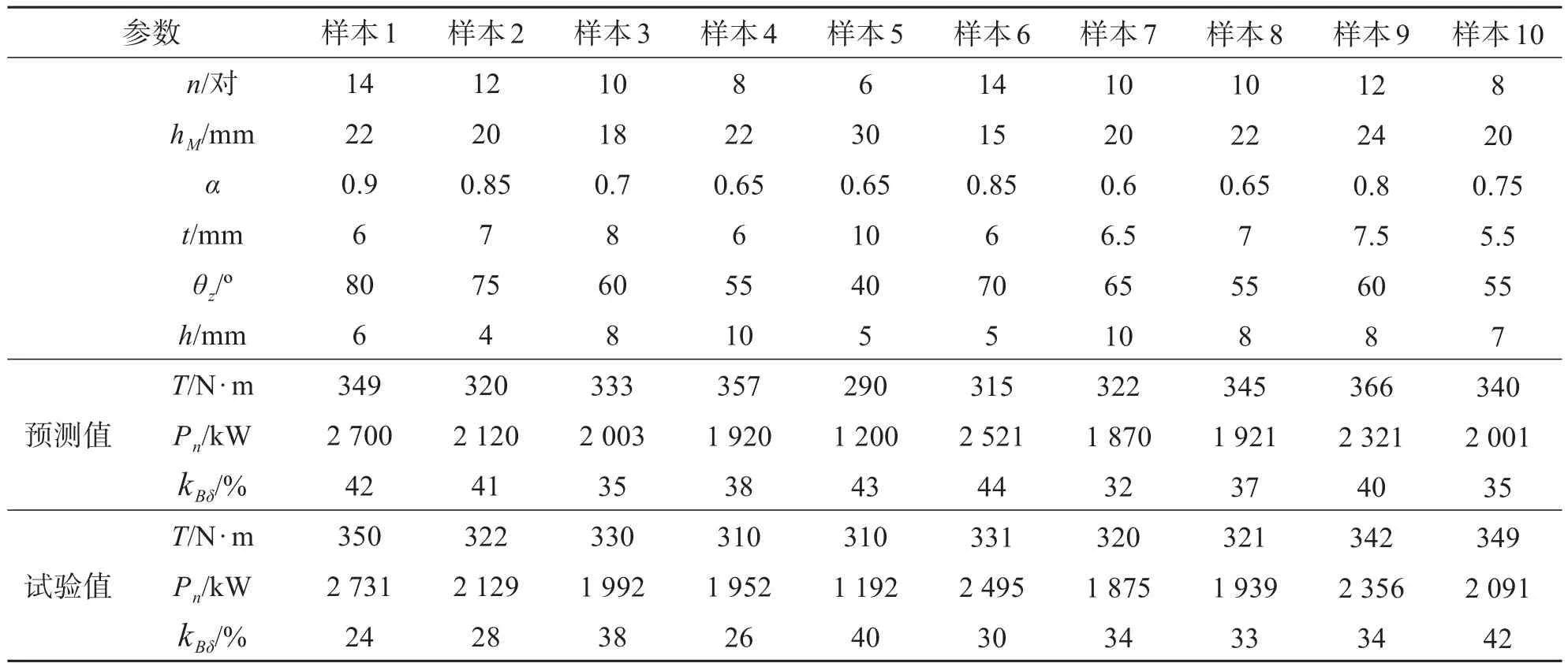
表3 BP网络预测和实验数据

通过表3可以看出，经过BP神经网络进行预测的数据和实验数据的整体走向大致相同，基本吻合，仅部分数据存在微小的偏差，这种偏差基本在允许范围之内，产生这种偏差的主要原因很可能是因为在数据选取时选取的样本略少或者是训练的样本集合过少，当然也不排除是由于外界因素产生的波动。为了能够对数据的精度进行进一步的确定，就必须进行更多的训练，由于本文仅对改进型永磁调速器进行分析，所以对此高精度实验不再作详细论述［3-6］。

3 改进后永磁调速器性能优化求解

前文采用BP神经网络对改进后的轴向永磁调速器成功地建立了预测模型，从而得到改进后的永磁调速器的涡流损耗P和输出转矩T，采用粒子群优化算法对数据进行优化处理，得到满足条件的结构参数。

3.1 空间粒子群优化算法

空间粒子群优化算法（SPSO）是标准粒子群算法（particle swarm optimization，PSO）的改进版算法，其结合了高度这一参数，将原本仅仅由速度作为主导算法元素的标准粒子群算法，改进成为由速度与高度同时起决定元素的算法，改进后的算法命名为空间粒子群优化算法。这种改进后的算法不仅让算法的优化更加全面，更会避免算法陷入局部最优且有助于粒子跳出早熟区间，相应的算法描述不在赘述。

在文献［5］中，主要采用经典的线性递减的方式，用来更新惯性权重ω，本文引用非线性递减更新ω，表达式为

3.2 改进后轴向永磁调速器性能优化流程

图4为改进后永磁调速性能优化流程图。

图4 优化流程

1）获取建模数据。运用BP神经网络对轴向永磁调速器进行优化，获得优化参数的组合集，应用Ansoft3D有限元仿真软件建立三维立体模型，并通过trainlm函数对建立的BP网络进行训练，最终输出转矩和涡流损耗，构造出训练数据集合，方便预测模型的建立。

2）运用BP神经网络建立输出转矩和涡流损耗的预测模型，并采用空间粒子群算法对预测模型进行验证。预测模型的精度主要受模型参数设定的影响，其设置的准确与否直接影响到预测模型的建立和实验仿真，采用k重交叉的验证方法精确地确定各参数数据。模型的各参数必须完全达到精度的要求范围，否则要重新对模型进行建立，直到模型合格为止。

3）运用空间粒子群优化算法对改进后的轴向永磁传动调速器的涡流损耗和输出转矩进行优化求解，同时对得到的结构参数建立Ansoft3D有限元仿真，验证其结果的合理性［7-10］。

仿真结果数据如表4所示。

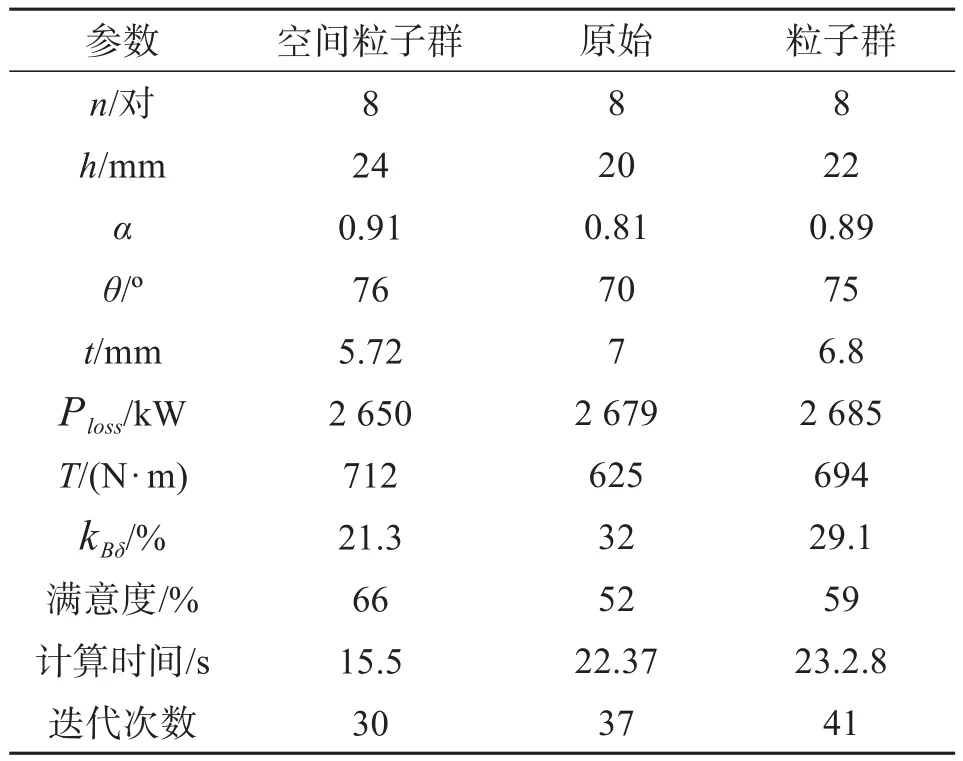
表4 仿真结果数据

由表4可以得出如下结论：

1）常规轴向永磁调速器的优化方法和粒子群永磁调速器优化方法均已应用于对轴向APMC的优化设计中，两种优化方法都得到了较好的优化效果。但经过对比发现，采用空间粒子群的优化方法结果更加理想，满意度高达66%。

2）对比常规轴向永磁调速器的优化方法和粒子群永磁调速器优化方法，本文采用的空间粒子群优化方法求解时间减少约6 s，可以看出该优化求解方法更迅速。

3）经对比发现，采用空间粒子群的优化方法，在求解过程中的迭代次数约减少7～11次，可见采用该优化方法求解更高效。

4 仿真研究

采用Ansoft3D软件分别对原始的、采用粒子群算法优化和采用空间粒子群算法优化的轴向永磁调速的扭矩、涡流和气隙磁密进行仿真分析，并将3种不同的轴向永磁调速器的仿真结果进行对比。

1）扭矩仿真

对3种不同的轴向永磁调速器的转矩进行仿真，图5为仿真结果，其中图a为原始轴向永磁调速器，图b为采用粒子群算法进行优化仿真的结果，图c为采用空间粒子群算法优化的仿真结果。

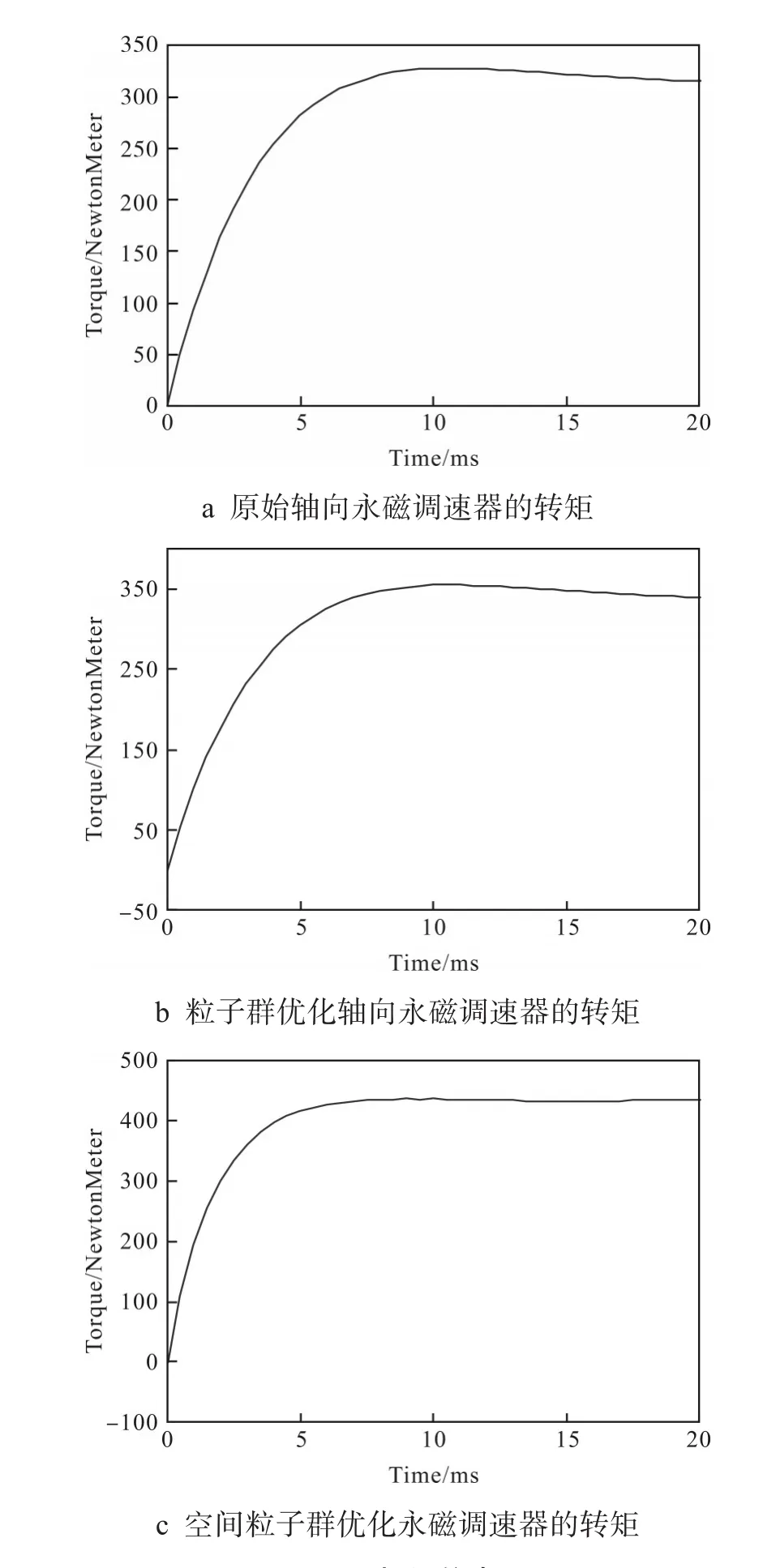
图5 扭矩仿真

从图5可以看出，采用原始轴向永磁调速产生的输出转矩约为325 N·m，采用粒子群优化方法的轴向永磁调速器输出的转矩约为350 N·m，采用空间粒子群优化方法的轴向永磁调速器输出的转矩为440 N·m，采用空间粒子群优化方法的轴向永磁调速器产生的输出转矩要高于前两种方法产生的输出转矩，所以采用空间粒子群优化方法是可行的，并且获得了明显的效果［11］。

2）涡流损耗（温度）

分别对3种优化方法设计的轴向永磁调速器进行铜转子热损耗的仿真，仿真结果如图6所示。

图6 铜转子热损耗仿真

图6中，通过对3种不同的轴向永磁调速器的铜转子热损耗的对比分析可以看出，采用原始优化方式的轴向永磁调速器的铜转子热损耗最大为7.865 1×107W/m2，采用粒子群方法优化的轴向永磁调速器的铜转子热损耗最大为6.931 6×106W/m2，采用空间粒子群优化的铜转子热损耗最大为2.931 7×106W/m2，采用空间粒子群优化的轴向永磁调速器铜转子产生的热损耗最小，这样在转矩传递过程中产生的效率就会越高，可以间接地证明此优化方法的可行性［12-13］。

3）气隙磁密波形畸变率

分别对3种优化方法设计的轴向永磁调速器进行气隙磁密的仿真，并将仿真结果进行傅里叶分解，图7中的a、b、c分别为采用原始优化方法、粒子群优化方法和空间粒子群优化方法的轴向永磁调速器的气隙磁密波形畸变率仿真结果。

从图7中可以明显地看出，3种对轴向永磁调速器的优化方法中，采用空间粒子群优化方法轴向永磁调速器经过傅里叶分解后的公共气隙中谐波含量相对较少，这可以说明本文优化的永磁转子结构以及优化算法能够有效减少其气隙谐波含量。

图7 气隙磁密波形畸变率仿真

5 结论

本文提出一种新型结构的改进型轴向永磁调速器，对改进型永磁调速器优化参数进行选择，并建立有限元仿真模型，结合BP神经网络对其进行优化设计，提出空间粒子群方法并对轴向永磁调速器预测模型进行优化求解，从而获得最优参数。最后，采用对比仿真形式证明此方法完全可以用于永磁调速器的优化设计并且效果较好，同时为其他大型传动设备优化设计提供了借鉴作用。