失效相关下齿轮传动系统的可靠性稳健优化设计

何永慧 刘 渊 刘国花 褚洪森 谭晓星 许航锋

(中国船舶重工集团公司第七一一研究所，上海 201108)

0 引言

齿轮传动系统失效通常存在多种潜在的失效模式，由于系统随机变量(如外载荷、几何参数和材料特性等)的同源性，失效模式间将存在不同程度的相关性[2,13]，即一种失效可能会加速(或减缓)另一种失效的发生。实际上，在可靠性设计过程中是否考虑失效模式间的相关性，对系统可靠性的估计有很大影响。失效模式独立假设通常会影响齿轮机构设计及其传动精度，而当失效模式间高度相关时，基于独立假设的可靠性设计往往会给出过于保守甚至不可接受的结果。因此，有必要在整个设计过程中引入概率相关性建模，以便为失效相关下的齿轮传动系统设计提供更加准确的可靠性评估和优化结果。

作为目前最广泛使用的方法，Pearson相关系数[15]只是对实际情况的一种线性近似，当极限状态函数呈现非线性且随机变量概率属性未知时，Pearson线性相关系数无法反映变量间真实的相关结构。因此，有必要提出一种更合理有效的建模方法，以实现不完全概率信息下齿轮传动系统失效模式的相关性建模。当前，Copula理论在构造多维变量的联合概率分布方面得到了广泛的应用[9,14,16]。Copula函数是一种将多变量联合分布函数与一维边缘分布函数连接起来的函数[18]。这种构造原理将概率分布的联合建模划分为两个方面，一个是对变量一维边缘分布的近似，另一个是边缘分布与特定Copula函数的连接。Copula方法已被证明是一种有效的数学建模工具，能够大大降低联合概率建模的难度。现有文献中已提供了多种常用的copula函数，如Gaussian、T、Clayton、Gumbel、Frank和Farlie-Gumbel-Morgensterm (FGM) copula等[23]。这些Copula函数依据其自身的结构形式，可以构造不同类型的相关结构。

许多文献从统计学[24]、水文学[25]、工程[12]等多变量建模的角度对Copula函数进行了研究，然而，Copula函数在机械设计领域还没有得到足够的重视，尤其是涉及具有相关失效模式的机械产品设计。齿轮传动系统作为一种重要的传动装置，其失效模式多种多样。虽然在设计优化和可靠性方面已有文献报道[3,19,21]，但仍然需要对齿轮传动系统的联合失效建模进行更深入的研究。

本文旨在研究在不完全概率信息和失效相关下，copula函数的选择对齿轮传动系统可靠性估计的影响，并开展可靠性评估及优化设计。鉴于不同失效模式间的相关结构可能是正相关或负相关等不同属性，为有效描述这些潜在的相关结构，需要通过对各种copula函数进行比较分析，进而提出一种相关失效下齿轮传动系统的可靠性设计方法。本文采用基于三阶矩的鞍点逼近技术计算了各失效模式的边缘失效概率[10]，基于不同copula函数的相关模型，运用可靠性界限理论对齿轮传动系统的系统可靠性进行了估计。

1 齿轮传动系统可靠性建模

由机械原理可知，齿轮传动系统失效时存在多种失效模式。为了研究齿轮传动系统各失效模式的可靠性和考虑失效相关的系统可靠性，首先建立了齿轮传动系统不同失效模式下的可靠性模型。

1.1 基于齿面接触强度的可靠性模型

齿轮的接触应力可用式(1)计算

σHZM-BZHZEZLSZβZK×

(1)

齿轮的接触疲劳强度可由式(2)计算

(2)

由此，齿面接触强度的极限状态函数可表示为

(3)

其中X1表示基本随机变量向量，且有

X1=[ZM-B,ZH,ZE,ZLS,Zβ,ZK,Fmt,dv1,lbm,KA,KV,KHβ,KHα,σHlim,ZNT,ZX,ZL,ZR,ZV,ZW]T

1.2 基于齿根弯曲疲劳强度的可靠性模型

齿轮的弯曲应力可由式(4)计算

(4)

齿轮的弯曲疲劳强度可由式(5)计算

(5)

小齿轮的极限状态函数可表示为

(6)

其中X2=[YFa1,Ysa1,Ye,YK,YLS,Fmt,b,mmn,KA,KV,KFβ,KFα,σF1lim,YST,YNT,YδrelT1,YRrelT1,YX1]T。

类似地，大齿轮的极限状态函数也可以表示为

(7)

其中X3=[YFa2,Ysa2,Ye,YK,YLS,Fmt,b,mmn,KA,KV,KFβ,KFα,σF2lim,YST,YNT,YδrelT2,YRrelT2,YX2]T。

如上所述，这里定义了齿轮传动系统的三种失效模式。从随机变量向量X1,X2和X3所包含的变量中可以看出，这些向量中包含有相同的随机变量，使得各失效模式间存在不同程度的相关性。因此，有必要建立各失效模式之间的联合概率分布，以准确描述失效模式间的相关属性。

2 齿轮传动系统可靠性估计

Abe Sklar首次在数学或统计意义上使用了“copula”一词[18]，用于描述将一维分布函数形成多变量分布的函数。这种建模方式意味着当边缘概率分布已知时，可采用copula函数来构建多个变量的联合概率分布函数。本文采用随机变量的统计矩信息，利用鞍点技术对边缘概率分布进行近似计算，进而采用copula函数对齿轮传动系统的相关结构进行描述，最终实现对系统的可靠性评估。

2.1 边缘失效概率估计

如上所述，齿轮传动系统中存在多种潜在失效模式，需要考虑不同失效模式间的相关性，并将其纳入可靠性分析过程中。根据Copula理论，一个联合概率分布函数可以分解为k个边缘分布函数和一个Copula函数，相应的Copula函数可以描述各个变量间的相关性。因此，首先必须确定每种失效模式的边缘概率分布。

本文采用基于矩的鞍点技术来逼近各失效模式性能函数的边缘概率分布。具有极限状态函数Y=g(X)的失效模式的失效概率可以表示为

Pf=P(Y≤0)=P(Ys≤-β2)=

(8)

式中，

Ys=(Y-μG)/σG

(9)

(10)

(11)

(12)

(13)

(14)

基于矩的鞍点逼近给出了一种有效而准确的边缘失效概率计算方法。该方法仅使用失效模式性能函数的前三阶矩，十分适于概率信息不完全的工程领域。

2.2 可靠性灵敏度分析

基于鞍点逼近方法，推导了随机变量分布参数的可靠性灵敏度。对式(8)进行偏导数求解，可得到分布参数均值的可靠性灵敏度，如下所示，

(15)

其中，

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

2.3 基于Copula函数的系统可靠性估计

Copula函数被广泛应用于描述随机向量之间的相关性，基于copula的技术可以作为多元分析问题的有效数学工具[17,20]。Copula函数是(0,1)中具有均匀边缘分布的随机向量的多元分布函数，它将边缘概率分布函数和联合概率分布函数进行解耦。下文将使用copula函数为不同的失效模式间建立二维相关性模型。

令Fi(Gi(X))和Fj(Gj(X))分别代表失效模式Gi(X)和Gj(X)的边缘分布函数，根据Sklar定理，两种失效模式的联合分布函数可以由式(25)表示

Fij(Gi,Gj)=C[Fi(Gi(x)),Fj(Gj(x))]

(25)

其中，C(u,v)表示二元Copula函数。

根据Copula理论，任意联合分布函数或密度函数均可通过一个含有待定参数的Copula函数进行建模。然而，不同失效模式间的相关属性差别较大，因此，有必要对比不同copula函数所代表的相关性特征，从而为每对失效模式确定一个最佳copula函数。本文在广泛使用的Copula函数簇中选择了部分常用的Copula函数，包括Gaussian、Clayton、Gumbel以及Frank Copula等，具体形式如表1所示。Gaussian Copula属于椭圆分布族，是多元正态分布与其边缘分布的连接函数。Gaussian Copula与多元正态分布的区别在于前者允许非正态分布和不同的边缘分布，而后者则不允许。表1中所列的Copula函数既能描述正相关特性，又能描述负相关特性，且待定系数限制在[-1,1]范围内。

表1 本文所采用的二元Copula函数

*u,v表示随机变量的边缘分布，θ表示copula的待定参数。

对于每个失效模式对，二维联合失效概率可由式(26)表示，

Pfpair=Pf[G1(x)≤0∪G2(x)≤0]=

Pf[G1(x)≤0]+Pf[G1(x)≤0]-

Pf[G1(x)≤0∩G2(x)≤0]=

Pf1+Pf2-C(Pf1,Pf2)

(26)

其中，C(Pf1,Pf2)表示采用Copula函数计算的联合失效概率。

系统可靠性界限理论是进行系统可靠性分析的常用方法，主要包括Cornell界限[4]和Ditlevsen界限[6]等。Ditlevsen界限也被称为窄界限，可通过评估每对失效模式的联合失效概率，得出系统失效概率的窄界限估计。对于具有m个失效模式的串联系统，系统可靠性估计的窄界限由下式给出：

(27)

其中Pfi表示第i个失效模式的失效概率，Pfij表示用Copula函数得到每对失效模式的联合失效概率。

本文采用Ditlevsen界限的上界来近似系统失效概率，即

(28)

本文采用表1所示的二元Copula函数，并将计算结果进行对比分析。由于失效模式间的相关性结构和关联度均未知，因此需采用统计方法估计每个Copula函数中的待定系数θ。在不同copula函数下进行系统可靠性计算流程主要包括三个步骤：

(1)对先前定义的齿轮系统的基本随机变量向量X1、X2和X3随机抽取n个样本，并获得各失效模式下响应(u)的样本。用MATLAB命令corr(ui,uj,'type','kendall')计算失效模式间的秩相关系数，继而估计Copula函数的待定参数；

(2)用摄动法对性能函数状态变量的高阶矩进行估计，继而采用基于矩的鞍点逼近方法估计各失效模式的边缘失效概率。需要注意的是，鞍点逼近的精度取决于统计矩的计算精度；

(3)根据所得到的边缘失效概率Pfi和联合失效概率Pfij，采用窄界限公式(28)计算系统失效概率，并对不同copula函数下所得的系统失效概率进行对比分析。

3 可靠性稳健优化设计

为了保证齿轮传动系统的稳健设计，将设计变量的可靠性灵敏度信息引入优化设计模型，建立了基于可靠性灵敏度的稳健优化设计模型。可靠性灵敏度反映了随机变量对系统可靠性的影响，通过限制可靠性灵敏度可以保证系统可靠性的稳健性，从而使得齿轮传动系统的可靠性在随机变量波动的情况下是稳定的。

根据可靠性稳健优化设计的定义，建立了齿轮传动系统的可靠性稳健设计优化模型，具体如下：

dL≤d≤dU,d∈Rndv

(29)

ωk=[f1(X*k)-f1(X*1)]/{[f1(X*k)-

f1(X*1)]+[f2(X*(k-1))-f2(X*2)]+

将平均粒径18 μm重质碳酸钙分别在900、1 000、1 100、1 200 ℃下煅烧4 h，后采用冶金石灰物理检验方法对石灰活性进行测试，结果如图1所示。

…+[fk(X*1)-fk(X*k)]}

(30)

同时，加权系数应满足以下条件

(31)

在可靠性分析的基础上，根据齿轮传动系统的可靠性稳健优化模型，可实现齿轮传动系统结构参数的优化设计。

4 数值算例

在本节中，针对具有随机结构参数的齿轮传动系统进行可靠性分析与稳健优化设计。齿轮传动系统随机变量的概率属性见表2，变量均服从正态分布。

表2 齿轮传动系统的随机变量

4.1 系统失效概率估计

根据前文所述方法，首先采用式(1)和式(4)分别计算了齿轮的接触应力和弯曲应力，然后，基于式(3)、式(6)和式(7)可分别建立齿轮传动系统的三种失效模式。考虑到系统的随机结构和设计参数，采用鞍点逼近和Copula函数分别估计各失效模式的边缘失效概率和失效相关下的系统失效概率。表3中列出了采用不同Copula函数以及独立假设下获得的系统失效概率，并结合Monte Carlo方法进行了相对误差分析。

由表3可见，在不同的Copula函数下，系统的失效概率差异很大。基于Gaussian Copula函数产生的相对误差为0.84%，说明在不确定失效模式间实际相关结构的情况下，最常用的Gaussian Copula函数适用于齿轮副的可靠性设计。通过对比可知，基于Clayton copula所得的系统可靠性相对误差最小。图1对比了Clayton Copula函数的散点图和失效模式g2、g3的随机样本散点图。可见，采用Clayton Copula能够较好地描述失效模式g2、g3之间的下尾相关性，即g2可靠性的降低将引起g3的可靠性亦随之降低。

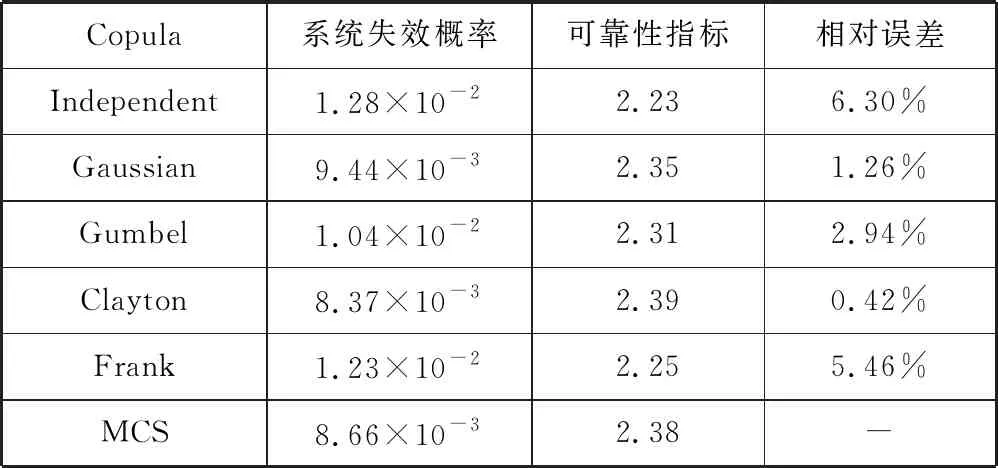
表3 不同copula函数下的系统失效概率

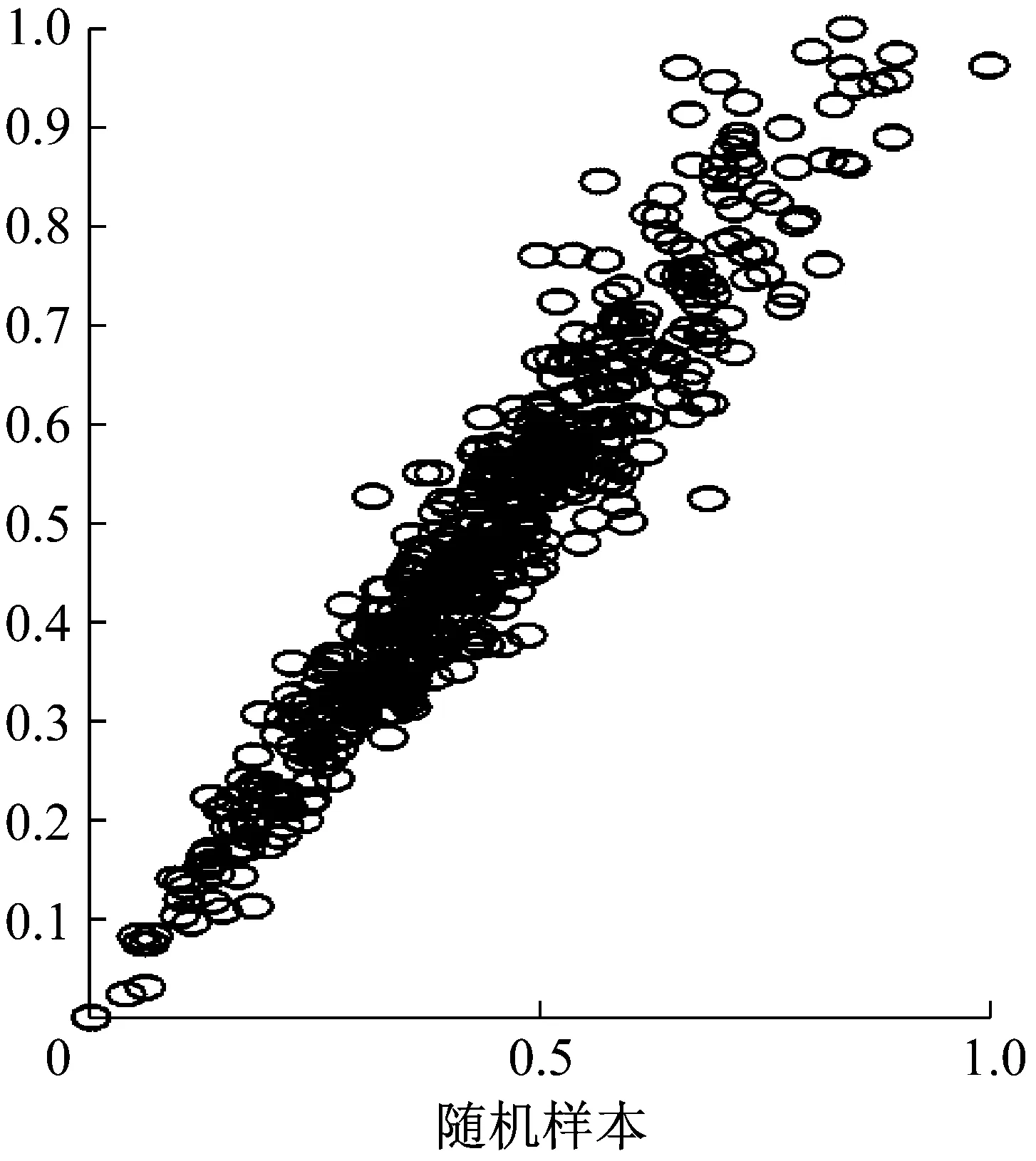
图1 随机样本和Clayton copula下g2和g3的散点图

Fig.1 The scatter plots forg2andg3under random samples and Clayton copula

4.2 齿轮传动系统的可靠性稳健优化设计

在采用Clayton Copula进行齿轮传动系统可靠性评估的基础上，进一步对随机变量的可靠性灵敏度进行分析。结合公式(15)-(24)，可得齿轮传动系统输入变量均值的可靠性灵敏度为：

∂R/∂X1=[0.0013,0.0007,0.0067,0.0088,

-0.4395,-0.1758,-0.4395,0.0791,

-0.3976,-0.3976,-0.3976,-0.3976,

-0.3976,-0.3976]

∂R/∂X2=[0.000012,0.00012,0.00018,0.0018,

0.0019,0.0053,7.0224,22.82,-3.476,

-2.317,-0.463,-2.155,0.0029,0.1865,

-4.6637,-3.8494,-4.4923,-4.0418]

∂R/∂X3=[0.0628,0.3138,0.0285,-0.0029,

-0.00062,0.00029,6.3398,21.13,-2.929,

-3.617,-0.493,-1.5932,0.9068,0.2257,

-4.4391,-3.2627,-4.4405,-4.4391]

从可靠性灵敏度的结果可知，随机变量dv1、lbm、b和mmn的可靠性灵敏度值相对较大，说明这些随机变量对系统的失效影响较大，其随机波动可能引起失效概率的显著变化。为了获得更可靠的系统可靠性结果，以下建立了包含可靠性灵敏度的可靠性稳健设计模型，

minf(d)=ω1f1(d)+ω2f2(h)

(32)

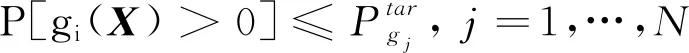
mmnL/Lm-1.5≥0;

8-mmnL/Lm≥0

z1-17≥0

36-z1≥0

b-0.2L≥0

0.35L-b≥0

其中，子目标函数f1(d)表示齿轮的体积，设计变量向量为d=[mmn,z1,b]T。子目标函数f2(h)将向量h1=[dv1,lbm,]T和h2= [b,mmn]T的可靠性灵敏度最小化。初始值设为d0=[2.6, 18, 30]T。表4列出了可靠性稳健优化的结果，可见，在满足预期可靠度的前提下，向量h1和h2中变量的可靠性灵敏度随之降低，齿轮传动系统的总体积也大大减小。此外，优化后的系统可靠性得到提高，且随着系统可靠性的提高，齿轮传动系统对随机变量波动的灵敏度随之降低，体现了较好的稳健性。

表4 基于Clayton copula的优化结果

5 总结

本文提出了一种相关失效模式齿轮传动系统的可靠性稳健设计方法。通过比较分析，确定了有效描述失效模式间相关结构的最佳Copula函数，并通过统计方法确定了Copula函数的待定系数。采用基于矩的鞍点法和窄界限理论，获得了系统的失效概率和可靠性指标。根据所得结果，可以得出以下结论：

(1)在描述不同失效模式间的相关结构时，不同的Copula函数将得到不同的失效概率估计结果。从实例中可以看出，使用Gumbel和Frank Copula低估了系统可靠性，而使用Gaussian和Clayton Copula得到的结果与仿真结果接近。

(2)通过比较不同Copula函数下的可靠度指标可知，采用Clayton Copula计算所得的可靠度指标结果最准确。Clayton Copula能够较好地描述随机变量间的尾部相关性，即当一种失效模式的可靠性降低时，与其相关的另一失效模式可靠性降低的可能性更大。

(3)在对齿轮传动系统三种失效模式的系统失效概率进行估计时，本文假定不同失效模式之间的相关结构均相同。然而，当失效模式数量增大时，不同状态变量间的相关结构将更加复杂。因此，如何合理确定多变量联合建模中的Copula函数，将是未来的主要研究内容。