基于分形维数的梗丝形态差异性评价方法

何超，李晓，晋照普，姚二民，丁美宙，姚光明，赵子龙，陈瑞倩

1 湖北中烟工业有限责任公司武汉卷烟厂，武汉市东西湖区环湖路66号 430040；

2 郑州轻工业学院，郑州市高新技术开发区科学大道136号 450001；

3 上海烟草集团有限责任公司北京卷烟厂，北京市通州区万盛南街99号 101121；

4 河南中烟工业有限责任公司技术中心，郑州市陇海东路79号 450000；

5 中国烟草总公司郑州烟草研究院，郑州市高新技术开发区枫杨街2号 450001

梗丝是卷烟配方的重要组成部分，具有填充性强、燃烧性好等优点，使用梗丝不仅可充分利用烟叶原料、节约生产成本，而且能够达到降焦减害的目的[1-4]。由于烟梗原料差异以及制梗丝工艺参数不稳定等因素，致使加工后梗丝形态分布存在较大差异，影响与叶丝的配伍性，进而影响到卷烟品质稳定性[5-8]。因此，对梗丝形态的差异性评价可为改善梗丝结构分布及优化成丝工艺参数提供指导。

分形理论是分析不规则物体几何属性的理论，是描述具有自相似自然现象的工具，包括数学上严格的自相似及统计意义上的自相似[9-11]；分形维数作为分形理论核心概念，是描述具有自相似性、不规则程度的定量参数[12-17]；通过分形维数可以透过复杂无序的自然现象及不规则的形态，来反映物体局部与整体之间的本质关联及其内在规律[13]，其在自然科学及社会科学的各个领域得到广泛应用[18-20]并涉及烟草领域；余娜等[9]基于分形理论建立了烟丝分布表征方法；齐婧冰等[21]以分形维数反映烟草冠层生长状况；杨小勇等[22]分析了烟叶质量分形特征。

梗丝形态作为烟梗加工成丝、成形后的一项重要评价指标，目前相关研究主要侧重于梗丝形态对卷烟质量影响[5-8]、梗丝形态模型及表征评价方法[23,24]、制梗丝工艺参数对梗丝形态影响[25,26]等方面，对于制得梗丝形态间的差异性分析尚无报道，而梗丝形态间差异性实质是梗丝内在结构自相似、不规则性及复杂程度的一种反映。因此，基于分形理论提出的分形维数，通过测量具有自相似、不规则性的梗丝形态特征参数周长、面积，利用“小岛法”[14,15]计算梗丝分形维数，分析对比梗丝内在结构单一形态梗丝分形维数的差异，并参照叶丝形态分析不同单一形态梗丝间的分形特性及差异性，建立梗丝形态差异性系数模型及评价方法以反映梗丝整体间的差异特性，旨在优化成丝工艺参数、改善梗丝形态结构，进而为提高卷烟品质的稳定性提供理论依据。

1 材料与方法

1.1 样品与仪器

具有代表性的5种不同单一形态[23]梗丝样品（单一形态分别为碎丝状、丝状、近丝状、近片状、片状）；黄金叶（大金圆）牌号配方叶丝（常规切丝宽度0.8～1.0±0.1 mm）；不同加工工艺处理的梗丝样品编号1#～6#（以不同比例、不同形态梗丝混合组成，河南中烟工业有限责任公司提供）。CCD图像采集系统CWT200（中国科学院安徽光学精密机械研究所）；AS400 Control筛分仪（德国Retsch公司）；PL203电子天平（感量：0.001 g，瑞士Mettle-Toledo公司）。

1.2 方法

1.2.1 样品的制备及图像采集

将样品置于恒温恒湿的环境中平衡48h[27]，参照文献[23]中筛分取样及图像采集方法，每个样品共取300根梗丝（分别取10次、每次30根），在相同的环境下依次完成样品的图像采集并保存。

1.2.2 梗丝面积和周长的测定

图像测量系统（Image-Pro Plus）经过标定后，建立图像中像素与实际空间尺度数据之间的关系[28]，将采集的梗丝图像载入到测量系统中，选用Irregular AOI（不规则图形光学检测）功能选取梗丝轮廓并标记，使用Count and Measure测量功能即可测得梗丝的面积（Area）、周长（Perimeter），如图1所示。

图1 梗丝外观轮廓提取标记及参数测量Fig.1 Extraction mark of outline of cut stems and parameter measurement

1.2.3 单一形态梗丝分形维数计算方法

分形维数是反映复杂物体不规则性的量度，测量方法有“小岛法”、相关函数法等[16,17]，由于梗丝形态的不规则性满足具有物理统计意义上的自相似性，因此可采用“小岛法”[14-15]计算其分形维数，不规则图形周长和面积之间具有如下关系：

式（1）两边同时取对数，则有

式中：P—梗丝周长；A—梗丝面积；C—常数；D—分形维数，为lnP～lnA双对数线性拟合方程直线斜率的2倍。

1.2.4 混合形态梗丝分形维数计算方法

由于实际生产制得的梗丝并非单一形态，而是由多种形态梗丝以不同的比例组成且均匀性差异较大。因此，为准确计算梗丝样品的分形维数，可将单一形态梗丝所占比例作为其分形维数权重，结合单一形态梗丝分形维数，即可得混合形态梗丝分形维数D，见式（3）。

式中：Di—对应单一形态梗丝分形维数；ti—对应单一形态梗丝权重，以百分数表示；i—单一形态梗丝分别为碎丝状、丝状、近丝状、近片状、片状。

1.2.5 梗丝形态指数均值计算方法

参照文献[24]中梗丝形态指数计算方法，采用算数平均法计算单一形态梗丝形态指数均值，加权平均法计算混合形态梗丝形态指数均值，计算方法见式（4）、（5）。

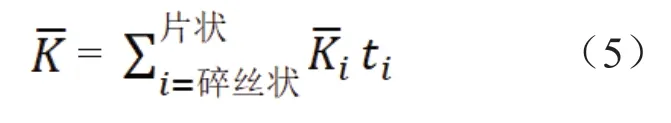
图2 单一形态梗丝及叶丝“小岛法”数据拟合结果Fig.2 Data fitting results of single morphological cut stems and cut tobacco based on slit island method

2 结果与讨论

2.1 单一形态梗丝及叶丝分形维数分析

测得单一形态梗丝及叶丝样品周长P、面积A后，根据1.2.3节方法采用最小二乘法进行线性拟合，结果如图2所示。

图3 单一形态梗丝及叶丝分形维数对比Fig.3 Comparison of fractal dimension bewteen single morphological cut stems and cut tobacco

图2可知，单一形态梗丝及叶丝在双对数坐标（x为LnA、y为LnP）下呈现较好线性关系，拟合方程决定性系数R2均达到0.850，且各拟合方程均方差均小于0.002、残差均±0.20以内，表明可用“小岛法”计算单一形态梗丝及叶丝分形维数。由图2计算单一形态梗丝及叶丝分形维数并做柱形图，如图3所示。

图3可知，叶丝及单一形态梗丝具有较好的分形特性且不同形态梗丝具有不同的分形维数；碎丝状丝状梗丝分形维数最小，片状梗丝分形维数最大，随着单一形态梗丝由碎丝状到片状的渐近变化，分形维数逐渐增大梗丝形态越来越不规则；其中，丝状梗丝分形维数略大于叶丝分形维数但数值上较为接近，实际丝状梗丝在形态及不规则性上与叶丝较为接近，而叶丝形态更为规则、均匀，因此叶丝分形维数相对较小。为直观的反映梗丝形态不规则性与分形维数之间的对应关系，选取实物外观进行对比，如图4所示。

图4 叶丝及单一形态梗丝外观特征Fig.4 Appearance characteristics of single morphological cut stems and cut tobacco

图4可看出，丝状梗丝与叶丝形态外观特征不规则性较为接近；随着梗丝形态由碎丝状到片状渐近变化，梗丝形态外观特征逐渐不规则，梗丝形态外观特征与上述分形维数测量值变化相吻合；并且梗丝在宏观结构以及微观尺度上是连续分布的，在一定尺度范围内具有一定的自相似性，因此梗丝形态的不规则性可采用分形维数进行描述且具有可行性。

2.2 梗丝形态差异性评价方法的建立

由于梗丝形态一致性差且差异性较大，并不像叶丝均可在常规烟支以及细支烟支中掺配使用。因此为反映梗丝形态间的差异性，参照叶丝形态指数及分形维数为标准，以梗丝形态指数及其分形维数反映梗丝形态的不规则性，通过梗丝与叶丝形态指数及分形维数的差异，间接反映梗丝形态的差异性，见式（6）、（7）。

式中：E—梗丝形态的不规则性；e—梗丝形态差异性系数；D′—叶丝分形维数；叶丝形态指数均值；D—D′ —梗丝与叶丝形态不规则性的差异；′—梗丝与叶丝形态间的差异。

根据1.2.4及1.2.6节方法，计算叶丝及单一形态梗丝分形维数与形态指数均值，并结合式（7）计算单一形态梗丝差异性系数，见表1所示。

表1 单一形态梗丝差异性系数Tab.1 Difference coefficient of single morphological cut stems

由表1可知，随着单一形态由丝状梗丝到片状梗丝渐近变化，Di—D′及差值逐渐增大，表明单一形态梗丝与叶丝相比不规则性及形态差异逐渐增大，并且单一形态梗丝差异性系数依次增大，即单一形态梗丝间的差异逐渐增大。为进一步建立梗丝与叶丝形态差异性间的关系，以5种单一形态梗丝与叶丝形态差异性为基准，选取梗丝形态差异性系数e为因变量，单一形态梗丝与叶丝不规则性差异性（Di—D′）及形态差异性指标为自变量，结合表1数据建立梗丝形态差异性系数回归模型，多元回归模型为Ye＝方差分析见表2。

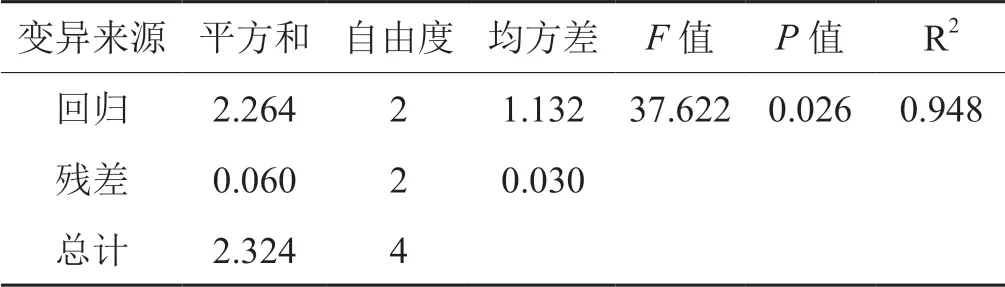
表2 回归方程方差分析表①Tab.2 Variance analysis table of regression equation

表2可知，所建回归模型决定性系数R2达到0.948，0.01＜P=0.026＜0.05，在显著性水平α=0.05时，F=37.622＞F0.05（2，2）=19。方差分析结果可知，回归模型具有统计学意义且模型R2较高，表明所建回归模型的可行性，通过回归模型可准确地估测梗丝形态差异性系数，以反映梗丝形态间的差异性。

由于实际生产切丝工艺参数不稳定致使制得的梗丝多以混合形态梗丝存在，即以多种单一形态梗丝以不同比例组成，且梗丝形态差异性系数各不相同。为通过梗丝形态差异性系数准确的反映梗丝形态均匀性间的差异，参考5种单一形态梗丝形态差异性系数，选取其中两组相邻梗丝形态差异性系数均值M1（0.491）及M2（1.189）为基准，将梗丝形态差异性系数从小到大依次划分为Ⅰ～Ⅴ 5个不同的差异性系数区间，如图5所示。

图5 梗丝形态差异性系数区间Fig.5 Difference coefficient interval of morphology of cut stem

根据图5所划分的梗丝形态差异性系数区间，对不同差异性系数区间梗丝形态差异性做定性分析，见表3所示。

表3 梗丝形态差异性评价方法Tab.3 Evaluation method for morphology difference of cut stems

2.3 验证分析

统计6组梗丝样品中单一形态梗丝权重比例，结合式（7）计算梗丝样品差异性系数实测值，采用所建差异性系数模型计算梗丝样品差异性系数估测值，见表4所示。

对差异性系数进行对比分析及相关性检验，实测值与估测值基本相吻合（图6），相关性系数r达到0.988（图7）相关性较强，表明梗丝形态差异性系数回归模型的准确可靠。

通过实测6组梗丝样品形态差异性系数可知，5#梗丝样品差异性系数介于Ⅰ区间（e＜0.491）形态差异性小；1#、2#样品介于Ⅱ区间（0.491＜e＜0.813）形态差异性较小；3#样品介于Ⅲ区间（0.813＜e＜1.189）形态差异性适中；4#梗丝样品介于Ⅳ区间（1.189＜e＜1.565）形态差异性较大；6#样品介于Ⅴ区间（e＞1.565）形态差异性大。为进一步验证分析选取梗丝实物外观进行对比（图8），可看出6组梗丝样品形态间差异性明显，1#、2#、5#样品梗丝形态差异性要好于3#、4#、6#样品，而实测梗丝形态差异性系数大小依次为e5＜e1＜e2＜e3＜e4＜e6，梗丝外观形态差异性与上述差异性系数分析相吻合，表明梗丝形态差异性评价方法在一定程度上具有可行性。

表4 梗丝形态差异性系数实测值与估测值Tab.4 Measured values and estimated values of difference coefficient of cut stem morphology

3 结论

图6 估测值与实测值对比Fig.6 Comparison of estimated and measured values

图7 相关性检验Fig.7 Correlation test

图8 梗丝样品外观对比Fig.8 Appearance contrast of cut stem samples

（1）单一形态梗丝拟合方程决定性系数R2均达到0.850，且均方差均小于0.002、残差均在±0.20以内，表明可用“小岛法”计算单一形态梗丝分形维数。

（2）梗丝形态具有较好的分形特性且不同形态梗丝分形维数具有明显差异，随着单一形态梗丝由碎丝状到片状变化，分形维数逐渐增大且梗丝形态越来越不规则，梗丝形态的不规则性可采用分形维数进行描述且具有可行性。

（3）以单一形态梗丝与叶丝的分形维数及形态指数的差异性为指标建立梗丝形态差异性系数模型，决定性系数R2达到0.948，方差分析表明回归模型具有统计学意义，模型经验证可准确估测梗丝形态间的差异性。

（4）初步建立了一种梗丝形态差异性评价方法，以差异性系数e为指标，梗丝形态间差异性小（e≤0.491）；差异性较小（0.491＜e≤0.813）；差异性适中（0.813＜e≤1.189）；差异性较大（1.189＜e≤1.565）；差异性大（e＞1.565）。