二次受力条件下粘贴加固受弯构件正截面承载力计算方法及影响

张永康

（济南市市政工程设计研究院（集团）有限责任公司，山东 济南 250101）

0 引言

粘贴加固就是将钢板或碳纤维复合材料（CFRP）等粘贴于构件受拉部位或者薄弱部位的面层，使其与结构形成整体，共同承受荷载，以提高原构件承载力的方法。其中，粘贴钢板加固与粘贴FRP加固两者的原理和计算方法在本质上是一致的，只是由于钢板和FRP材料性质不同而略有不同。结构自重一般较大，再加上施工时的其他荷载作用，将会使桥梁结构在进行粘贴加固时已有了相当的应力应变储备。但加固后新增钢板或CFRP只承受加固后荷载产生的效应。因此已有荷载对加固效果的影响是不应被忽略的，分析二次受力对加固效果的影响是十分必要的。本文整理综合了二次受力条件下粘贴加固受弯构件正截面承载力的计算方法，并且分析了二次受力对加固效果的影响。

1 基本假定

（1）加固后构件变形仍符合平面假定，即混凝土和钢筋的应变沿截面高度符合线性分布。

（2）截面受压区混凝土的应力图形采用等效矩形。

（3）不考虑受拉区混凝土的作用，拉力全部由钢筋承担。

（4）原受力钢筋及钢板均为理想弹塑性材料，FRP为理想线弹性材料，且文中的极限应变均指材料设计强度对应的应变值。

（5）粘贴物与混凝土之间粘贴良好，不发生黏结剥离破坏。

（6）粘贴物厚度较小，忽略不计。

2 二次受力条件下粘贴加固受弯构件正截面承载力的计算方法

2.1 加固后受弯构件正截面破坏形态

粘贴加固的受弯构件一般不会出现少筋梁的破坏形态，因此可以把在二次受力条件下受弯构件破坏形态分为以下四种：

（1）原受拉钢筋未屈服，粘贴物未达到设计强度，受压区边缘混凝土被压碎。

（2）原受拉钢筋屈服，粘贴物未达到设计强度，受压区边缘混凝土被压碎。

（3）原受拉钢筋未屈服，粘贴物达到设计强度，受压区边缘混凝土被压碎。

（4）原受拉钢筋屈服，粘贴物达到设计强度，受压区边缘混凝土被压碎（粘贴钢板加固）或未被压碎（粘贴CFRP加固）。

第一种及第二种破坏形态对于粘贴钢板加固与粘贴CFRP加固是相同的；第三种破坏形态是少数加固材料使用较多且初始荷载较小的加固情况才具有的破坏形态；对于粘贴钢板加固，第四种破坏形态是钢板屈服后中性轴上升，混凝土受压区高度减小，直至受压区混凝土被压碎；对于粘贴CFRP加固，第四种破坏形态则是CFRP材料直接被拉断，构件破坏，受压区混凝土未被压碎。

2.2 相对界限受压区高度

二次受力条件下粘贴加固受弯构件的四种破坏形态对应着两个相对界限受压区高度：ξ1和ξ2。其中，ξ1对应原受拉钢筋屈服的同时受压区边缘混凝土被压碎；ξ2对应粘贴物达到设计强度的同时受压区边缘混凝土被压碎。计算公式为：

式中：ξb按照《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG D62—2004）规定选用；[εz] 为粘贴材料的极限应变；ε1为加固时原构件初始应变，即滞后应变，按《混凝土结构加固设计规范》（GB 50367—2013）规定计算。

2.3 正截面承载力Mu的计算

首先假设所有材料在破坏时均达到设计强度，此时由ΣX=0可得：

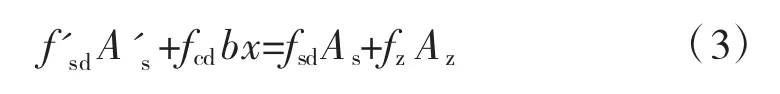
求得受压区高度x后，按以下方法计算：

（1）若 2a's≤x≤ξ2h，则属于第四种破坏形态（见图1）。对于粘贴钢板加固，对受拉钢筋合力点取矩可得

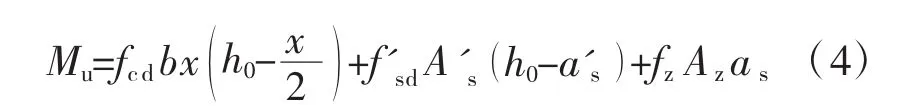
图1 第四种破坏形态下正截面承载力计算

对于粘贴CFRP加固，偏安全地将混凝土受压区应力图简化为高度为ξ2h的矩形应力图，并忽略受压钢筋的应力。此时对混凝土受压区合力点取矩可得

（2）若x＞ξ2h，则破坏时粘贴材料未达到设计强度。此时应按下式重新计算混凝土受压区高度x：

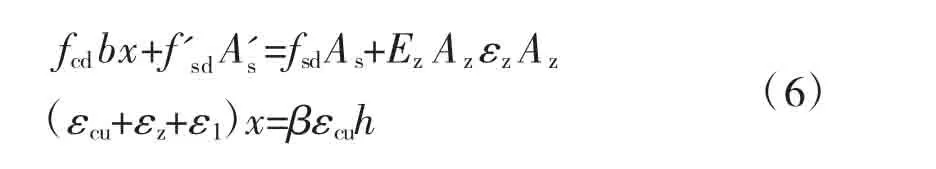
用此时求得的x进行破坏形态判断：若x＞ξ1h0，则属于第一种或第三种破坏形态，是脆性破坏，应重新设计予以避免；若x≤ξ1h0，则属于第二种破坏形态（见图2a），此时对受力钢筋合力点取矩可得：

（3）如图 2b 所示，若 x＜2a's，且 x≤ξ2h，对受压钢筋合力点取矩可得：

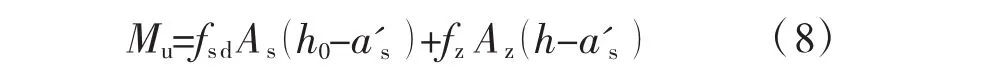
若 x＜2a's，且 x＞ξ2h，则需先用式（6）重新计算x，然后对受压钢筋合力点取矩可得：

以上式中：Ez为粘贴材料的弹性模量；εz为破坏时粘贴材料的应变；Az为粘贴材料的面积。

3 二次受力对加固后承载力的影响

3.1 二次受力对相对界限受压区高度ξ2的影响

由式（2）可以看出，随着初始应变ε1的增加，ε1是不断减小的。假定加固前的最大滞后应变为原受拉钢筋的屈服应变，最小滞后应变为零。现在针对最小和最大滞后应变，计算不同材料加固后的ξ2值，结果见表1。

图2 ξ2h＜x≤ξ1h0与 x＜2a's时的正截面承载力计算

由表1数据可知，钢板加固后的ξ2值远大于CFRP加固后的ξ2值，并且滞后应变对钢板加固后的ξ2值影响较大，而对CFRP加固后的ξ2值影响不大。这主要是因为钢板的极限应变只有0.001 5，远小于CFRP材料的极限应变最大值0.01。这就使得在构件变形不大、实际混凝土受压区高度还较大时，钢板就可以达到极限应变，而CFRP材料在构件具有较大变形和较小的混凝土受压区高度时，才可以达到极限应变，即钢板加固后的ξ2值远大于CFRP加固后的ξ2值。滞后应变ε1大小同钢板材料相近，与CFRP材料的相差10倍左右。由式（2）可以看出，这就使得滞后应变的改变对钢板加固后ξ2值的影响较大，而对CFRP加固后的ξ2值影响较小。

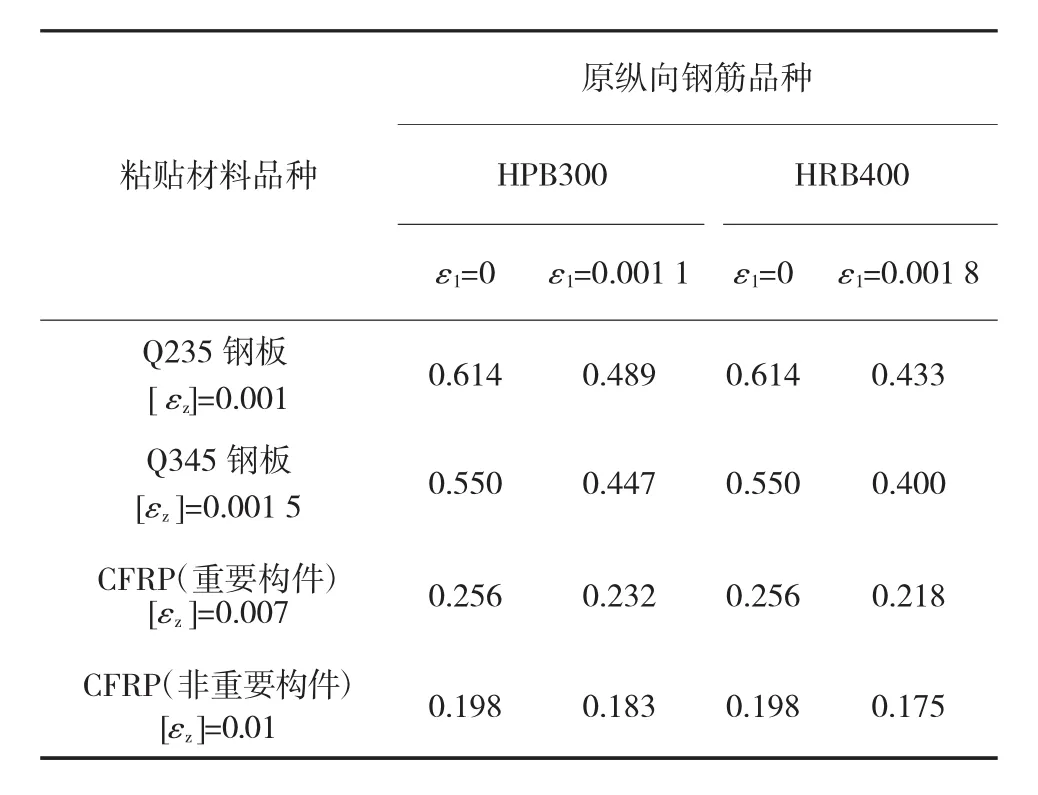
表1 不同加固材料加固后的最小和最大ξ2值

表1中钢板加固后的ξ2值与相应的ξb值相比较，可以发现两者相差不大，再加上h＞h0，ξ2h与ξbh0值会更接近，甚至出现 ξ2h＞ξbh。也就是说加固量适当的钢板加固构件的混凝土受压区高度x一般都会满足x＜ξ2h，而加固后满足x＞ξ2h的只是一小部分。

3.2 二次受力对承载力的影响

二次受力对粘贴加固受弯构件正截面承载力的影响是同加固后梁的破坏形态联系在一起的。

（1）x≤ξ2h时，破坏时加固材料均能达到设计强度，二次受力对承载力没有影响，直接按式（4）或式（5）进行计算。由上面分析可知钢板加固后构件的混凝土受压区高度x一般都会满足x≤ξ2h，因此二次受力对大部分钢板加固影响不大。

（2）x＞ξ2h时，破坏时加固材料未能达到设计强度，二次受力对承载力是有影响的。随着滞后应变的增加，破坏时加固材料的应变会减小，进而使承载力下降。滞后应变对承载力的这种影响具体有多大，可以做一下定性分析：

在式（6）的第一式 fcdbx+f'sdA's=fsdAs+EzεzAz中，f'sdA's和fsdAs对于某一具体截面是一个定值，因此混凝土受压区高度x的变化值Δx取决于EzεzAz（相当于加固后承载力提高幅度）和Δεz/εz（滞后应变引起的破坏时粘贴材料应变减小值占原来材料应变的比值）。CFRP加固的特点是加固面积较小，但破坏时 CFRP应变较大，一般 εz都会达到0.005。滞后应变ε1最大值一般小于0.002，与之相对应的 Δεz在 0.001左右，Δεz/εz在 0.2左右，也就是说由最大滞后应变引起破坏时，CFRP应变的减小值只是没有滞后应变条件下构件破坏时CFRP应变的20%。所以Δεz引起的Δx值较小，相应的承载力变化也较小，滞后应变对CFRP加固受弯构件正截面承载力影响不大。

3.3 计算例题

已知双筋梁截面尺寸b×h=200 mm×500 mm，as=60 mm，a's=35 mm，混凝土强度为 C20，fc=9.6 MPa，HRB335 钢筋fy=f'y=300MPa，As=804mm2，A's=226mm2，Es=200 GPa。在此梁底部采用粘贴法加固：

（1）若粘贴碳纤维布两层，每层厚0.1 mm，碳纤维布弹性模量Ez=230 GPa。

（2）若粘贴钢板两层，每层厚1 mm，钢板弹性模量Ez=200 GPa。

求加固后所能承受的弯矩值。计算结果见表2、表 3。

表2 不同滞后应变条件下CFRP加固后的计算结果

表3 不同滞后应变条件下钢板加固后的计算结果

计算结果与理论分析吻合较好：滞后应变从零增加到最大，CFRP加固后正截面承载力只下降了3.1%；钢板加固后，虽然承载力提高了48.82%，但是x仍满足x≤ξ2h，二次受力对承载力没有影响。变形的影响不大，对此有必要进一步研究。

（5）本文只是对二次受力条件下粘贴加固后受弯构件正截面承载力的理论研究，有必要对此进行试验研究，以检验理论的正确性。

4 结 语

（1）本文归纳总结了二次受力条件下粘贴加固后受弯构件正截面承载力的系统计算方法。

（2）二次受力条件下，随着滞后应变的增加，加固后ξ2值会减小，对于钢板加固后ξ2值影响较大，而对于CFRP加固后ξ2值影响较小。

（3）当混凝土受压区高度x＞ξ2h时，二次受力会使承载力下降，但是对于粘贴CFRP加固影响较小；当x＜ξ2h时，二次受力对承载力没有影响，钢板加固后的ξ2h值一般与ξ1h0相差不大，x一般都满足x＜ξ2h。总的来说，当加固后承载力提高不是很大时，二次受力对粘贴加固后受弯构件正截面承载力影响较小，可以不予考虑或简化计算。

（4）二次受力对粘贴加固受弯构件的极限承载力影响不大，并不等同于对屈服承载力和构件