中国国债对经济增长的非对称影响效应研究

单飞 郑义汀

摘 要：本文在回顾国内外文献的基础上，利用国债负担率为转换变量的平滑转换模型（STR）和面板平滑转换模型（PSTR），对国家层面和省际层面国债负担率对经济增长率的影响进行了经验研究。得到如下结论：（1）在国家层面，国债对经济增长的促进作用处于低区间，即过重的国债负担会降低国债对经济增长的促进作用。（2）在省际层面，国债对经济增长具有正效应且呈现非对称性。不同地区、不同时期国债负担率的阶段转换会导致国债负担率对经济增长率的反应系数具有地区异质性和时变性。

关键词：国债负担率;经济增长;GDP增长率;平滑转换模型（STR）;面板平滑转换模型（PSTR）

中图分类号：F810.5文献标识码：A

文章编号：1000-176X（2019）03-0083-07

一、问题的提出

随着中国经济发展速度的日益加快，国债作为重要的宏观经济变量与经济增长的联系更加密切。因此，研究国债对经济增长的影响效应，找出国债负担率对经济增长率的作用渠道，探究适度的国债规模已是当务之急。中国目前所面临的地区之间发展不平衡问题日益严重，沿海地区与中西部地区的经济发展差距愈发悬殊，深入研究不同省际间国债对经济增长的影响对于中央统筹兼顾调整经济政策具有重要的参考意义。

西方学者对于国债问题的研究起步较早，有基于李嘉图等价的国债无用论、强调挤出效应的国债有害论和凯恩斯主义的国债有益论等。Kimbell和Mankiw[1]把政府举债和征收所得税对私人消费的影响作为研究重点，发现随着样本数据时间的变化，所得税对私人消费可能产生正面效应，也可能产生负面效应。Pelagids和Desli[2]通过对欧洲数据进行分析结果表明，国债能够促进经济增长。Gierner和Kauermann[3]认为，GDP对于国债的弹性系数为正，对经济增长具有显著正影响，但当国债的规模超出一定范围时，正效应明显减弱。Panizza和Presbitero[4]研究发现，国债与经济增长之间虽然呈现负相关关系但是并不存在因果关系。Forslund等[5]通过发展中国家和新型市场国家的数据发现，国债与通货膨胀之间相关性较弱。Borensztein等[6]在Eichengreen和Luengnaruemitchai[7]研究的基础上发现，股票市场的发展与贸易开放度和国债规模之间存在正相关关系。

国内对于国债的研究主要有以下三个方面：一是在国债对经济增长影响方面，刘溶沧和马拴友[8]认为，如果是由于加大公共投资而导致财政赤字，那么财政赤字和发行国债对宏观经济的净效应显著为正。王维国和杨晓华[9]支持刘溶沧和马拴友[8]的看法，认为当国债主要进行公共投资时呈现出对经济增长显著的正效应。李戎等[10]认为，中国国债规模现阶段并未表现出明显的阈值，且对经济增长未呈现出显著的抑制作用。二是在国债对总需求影响方面，高培勇[11]认为，发行国债会刺激社会总需求的增加，其结果是提高了社会总消费和降低了社会总投资。罗嗣红[12]、宋福铁[13]以及杨文奇和李艳[14]指出，发行国债增加公共投资会对民间、私人等其他类型的投资产生带动作用。三是在国债规模及风险方面，陈共和类承曜[15]采用国债负担率和债务依存度这两个指标通过分析发现，当前中国的国债规模仍处于可控制的范围内。刘邦驰[16]指出，度量国债规模的国际公认指标需与各个国家经济发展水平、时代背景紧密结合在一起，并且指出当前中国政府举债尚未达到极限，国债还有一定的增发空间。

综上所述，大部分学者认为国债对于经济增长具有促进作用，但普遍聚焦于国家层面的研究，由于缺少统一的省际国债负担率指标，对于省际层面国债对经济增长影响的研究比较缺乏。同时，部分学者研究了国债负担率对经济增长率的非线性效应，但是所采用的阈值模型解释能力有限，无法捕捉影响机制的平滑转换趋势。因此，在国内外已有文献的基础上，本文采用国家层面及省际层面国债负担率数据，构建了国债负担变动下国债负担率对经济增长率的理论模型，利用平滑转换模型研究了以国债负担率为转换变量条件下国债对经济增长的非对称效应。

本文从以下两方面进行了扩展：首先，基于面板平滑转换模型（PSTR）分析了省际国债的非对称影响。其次，兼顾国家层面及省际层面国债对经济增长的影响，分析具有代表性省份的国债对经济增长的地区异质性及时变性。本文剩余部分的结构如下：第二部分是模型设定、变量选择及数据来源。第三部分是国家层面国债负担对经济增长非对称效应分析。第四部分是省际国债负担对经济增长非对称效应的经验分析。第五部分是结论与政策建议。

二、模型设定、变量选取及数据来源

（一）模型设定

1.平滑转换模型

平滑转换模型（Smooth Transition Regression Model，简称STR）是分析经济问题时经常采用的一种非线性模型。经济变量相互之间影响机制的转换往往不是一个突变过程，而是呈现出一种连续的渐变过程。平滑转换模型通过引入转换函数能够较好地捕捉和解释这一渐变过程。標准的STR模型由线性部分和非线性部分组成，模型的基本结构如下：

（二）变量选取及数据来源

本文聚焦于国债对经济增长的影响，国家层面国债负担指标选取国债负担率（国债余额/GDP×100%），经济增长指标采用实际GDP增长率。同时，由于省际层面国债没有明确指标，本文为了分析各省国债负担情况，引用李戎等[10]的办法，利用各省上交中央的税额占中央税收收入的比重来衡量各省份对国债的分担程度，作为各省份国债负担率指标。数据处理过程中选取了中央税收收入来源中的主要税种，包括增值税、消费税、企业所得税和个人所得税来计算各省国债分担率[10]。经济增长指标采用各省实际GDP增长率。

本文经验分析所采用的数据来源于《中国统计年鉴》、中经网数据库和Wind金融终端数据库。在国家层面，时间区间为1985—2017年，共33年的年度数据，以1985年为基年。本文采用字母y代表GDP增长率，debt代表国债负担率。在省际层面，受制于税收数据的可得性，时间区间为1998—2016年，共19年的年度数据，以1998年为基年。受限于数据，在本文的分析中不包括港、澳、台在内，共31个省份，即N=31，用i代表省份，t代表年份。

三、国债对经济增长非对称效应的经验分析

（一） 单位根检验与协整检验

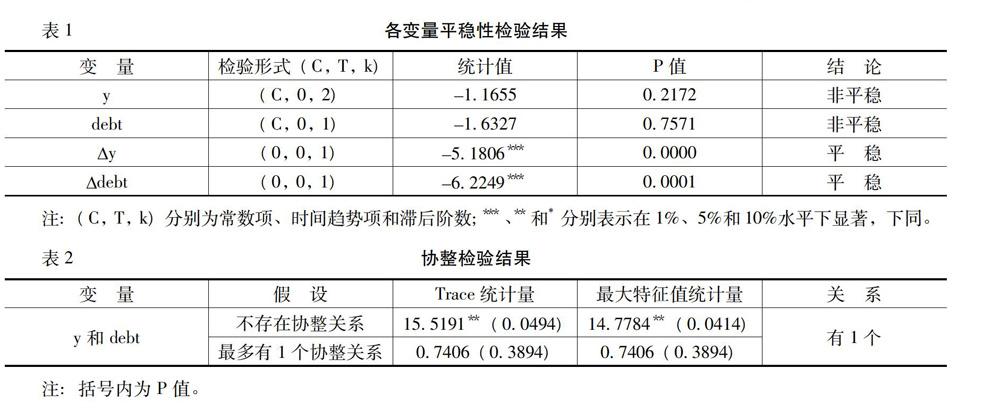
在进行经验分析之前，先需要对各时间序列变量进行平稳性检验。采用单位根检验方法对各时间序列数据进行平稳性检验，具体的检验结果如表1所示。由表1可知，GDP增长率、国债负担率的原序列都是非平稳序列即存在单位根。但是两个变量在一阶差分去除趋势项之后全部都为平稳序列，具备进行下一步检验的条件。

对于没有协整关系的单整变量进行回归分析仍然是伪回归，需要在建模分析之前进行协整检验，检验结果如表2所示。由表2可知，国债负担率与GDP增长率之间存在协整关系，即两者之间存在长期均衡关系。

（二）确定滞后阶数

在估计STR模型之前需要确定最大滞后阶数，可以借助VAR 模型中滞后阶数的选取方法来实现。

（三）转换变量选择

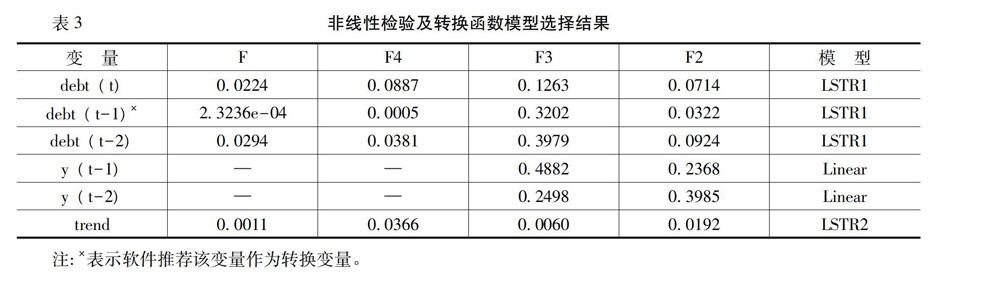
由于我们确定的最大滞后階数为2阶，因此，模型的潜在转换变量有debt（t）、y（t-1）、debt（t-1）、 y（t-2）、debt（t-2）和趋势项（trend），对模型的线性假设检验和各潜在转换变量及对应的转换函数形式的选择结果如表3所示。

（四）模型参数估计值

在确定了c及γ的初始值后，就可以进行非线性模型参数估计，估计结果如表4所示。其中，AIC=-8.4940，SC=-7.9851，R2=0.8452，2=0.8502。

根据转换函数G（debt（t-1），γ，c）中的参数估计结果，斜率参数 γ=24.1491，数值较大，说明模型转换函数的调整速度较快，即模型在两体制之间的转换速度较快。从表4中位置参数估计结果c=0.0444来看，转换函数G（debt（t-1），γ，c）呈现以参数c为对称中心的机制转化形式。当转换变量debt（t-1）较小，且小于位置参数c时 （c=0.0444），此时转换函数的值趋于零，模型的非线性部分约等于零，LSTR模型简化为普通线性模型。当期的国债负担率debt（t）系数为-24.9490，说明当期的国债对经济增长有负面效应。滞后一期的国债负担率debt（t-1） 与GDP增长率 y（t） 呈负相关，系数为-0.8291，但系数较小，说明滞后一期国债负担率对当期GDP增长率的影响较小。滞后两期国债负担率debt（t-2）系数为34.7249，说明滞后两期国债负担率对GDP增长率有着较大的促进作用。

当转换变量debt（t-1）较大，大于位置参数c时（c = 0.0444），转换函数趋于1，国债负担率与经济增长率呈现明显的非线性特征。此时当期的 debt（t）和y（t）呈正相关，系数为0.2609，当期国债负担率开始对经济增长率显现正效应。滞后两期的debt（t-2）与y（t） 也呈现正相关，系数为0.5558。总体来看，当国债负担率高于位置参数时，国债对于经济增长仍然保持促进作用，但是与转换变量小于位置参数的情况相比，其对经济增长的促进作用要小得多，过重的国债对私人投资造成较大的挤出效应，降低了经济运行效率，即过重的国债会降低国债负担率对经济增长率的正面促进作用。

与传统的线性模型相比，采用LSTR1模型来描述国债负担率与GDP增长率之间的动态关系时具有比较明显的优势。首先，LSTR1所生成的拟合数据的曲线变化趋势与原始序列的曲线变化趋势非常吻合，说明本文采用LSTR1模型所估计出的非线性模型可以很好地解释国债负担率与经济增长率之间的动态关系。其次，LSTR1模型由于转换函数的存在，能够更有效地洞悉到国债负担率与经济增长率在不同国债负担背景下的非线性动态转换关系，这是传统线性模型所不能实现的。

四、省际国债对经济增长非对称效应的经验分析

（一）非线性检验

本部分主要研究的是省际国债负担率对各省GDP增长率是否存在非线性关系，并探究其影响变化的具体机制。因此，首先要对GDP增长率是否为非线性进行检验。

LM_X表示基于渐进卡方分布的LM检验的统计值，LM_F表示基于渐进F分布的LM检验的统计值。由两个统计量的P值检验结果可知，这两个统计量都在1%的显著性水平下拒绝了模型为线性的原假设。因此，选择国债负担率作为转换变量对GDP增长率存在非线性的影响。采用面板平滑转换模型能够较好地体现变量之间的非线性特征。

（二）转换函数个数检验

转换函数个数检验结果如表5所示。

由表5第二行的统计量LM_X和统计量LM_F的结果和对应的P值可以看出，LM_X统计量和LM_F统计量都在1%的显著性水平下拒绝β3=0的原假设。从第三行统计量LM_X和统计量LM_F的结果和对应的P值可以看出LM_X和LM_F统计量在10%显著性水平下不拒绝β2=0 |β3=0的原假设。第四行统计结果表明LM_X和LM_F统计量在1%显著性水平下拒绝β1=0 |β2=β3=0的原假设，因此，应该选择转换函数个数m=1，采用LSTR1模型，即面板平滑转换模型存在一个转换函数。

（三）模型估计

（四）转换函数的特征分析及经济含义

根据面板平滑转换模型（PSTR）的形式和估计结果可知，当期国债负担率debt（t）对GDP增长率影响的反应系数为α+β1G（·），反应系数中线性部分的系数为α，非线性部分的系数为β1G（·），转换函数G（·）满足面板平滑转换模型的LSTR1形式。为了便于分析不同国债负担率对GDP增长率的转换特征，转换函数G（debt（t），γ，c）与转换变量debt之间关系的图形图形省略，留存备索。，如图1所示。模型中可知，位置参数c=0.0512，当国债负担率debt小于0.0512时，转换函数G（debt（t），γ，c）小于0.5000，否则G（debt（t），γ，c）大于等于0.5000，并且当debt大于0.0800时，转换函数G（debt（t），γ，c）约等于1。

结合转换函数图形与表6的实证结果可得，在转换函数中国债负担率存在位置参数c=0.0512。并且该转换机制中斜率参数为357.5260，状态转换十分迅速。说明中国国债负担率对GDP增长率的影响随着不同年份不同省份国债负担率的变动而有所不同。因此，中国各省份国债负担率对经济增长率影响的反应系数存在时变性和地区异质性。在以上分析的基础上，可以得出样本数据中各省份随着时间变化国债负担率对经济增长率的反应系数。

为了描述不同国债负担阶段中，国债负担率对GDP增长率的反应系数，本文将中国按国债负担率程度大小划分，并从全国范围内挑选出具有代表性的省份：北京、上海、甘肃和辽宁作为代表。据测算，上海的国债负担率在0.0880—0.1300之间波动，位于高国债负担区间，代表了最高国债负担水平。北京的国债负担率在0.0388—0.1813之间，国债负担变化跨度较大。甘肃的国债负担率在0.0060—0.0120之间，属于国债负担较低区间。辽宁的国债负担率在0.0540—0.0260之间，国债负担低于上海高于甘肃，但与其他三省份的一个显著区别在于国债负担随时间而递减。

本文挑选这四个省份作为不同国债负担程度的典型代表，考察不同国债负担阶段下，国债负担率对GDP增长率的反应系数的时变性、省份异质性和各省的共性，能够比较准确地捕捉到中国不同国债负担阶段各省份的典型特征及影响机制。

（五）国债负担率对经济增长率具有差异化的影响

由表6可知，当期国债负担率对GDP增长率的反应系数为α+β1G（·），其中，α=0.7480，β=-0.5924，体现出国债负担率对GDP增长率的促进作用存在于反应系数的线性部分，对GDP增长率的抑制作用存在于非线性部分，说明国债负担率通过两种渠道影响经济增长：第一种是直接效应，国债负担直接提升经济增长;第二种是间接效应，根据国债负担率的不同阶段间接地对经济增长产生抑制作用。因此，随着国债负担阶段的转换，国债负担率对GDP增长率的影响呈现差异化的特征。

1.上海处于高国债负担阶段，国债促进经济增长作用最小

上海国债负担率对GDP增长率具有正的影响系数，即国债负担有利于提升经济增长率。上海国债负担大于0.0800，转换函数约等于1，此时反应系数为0.1557。由于上海国债负担已位于高机制区间，因此，继续增加国债并不改变转换函数及反应系数的值，此时国债对于上海经济增长的作用最小。上海作为长三角的经济重镇，在经济发展中一直扮演着举足轻重的角色，其税收占比也一直居高不下，反映出其强大的经济实力。应该注意到的是，作为高国债负担的代表省份，国债对上海经济增长的作用虽然仍是正向，但已进入最低值。较重的国债对上海私人投资的挤出效应十分明显，使得国债促进经济增长的作用降到最低值。

2.甘肃处于低国债负担阶段，国债促进经济增长作用最大

甘肃国债负担率对经济增长率具有正的影响系数，即国债负担率有利于提升经济增长率。甘肃国债负担率小于0.0120，转换函数约等于零，此时反应系数为0.7481。甘肃国债负担位于低机制区间，国债对于甘肃经济增长的作用显著，且反应系数最大。甘肃通过税收分担的国债水平也远低于东部省份。低水平的国债对甘肃私人投资的挤出效应十分微弱，因此，国债对经济增长的促进作用始终处于最高值。

3.北京國债负担加重，国债促进经济增长作用减弱

北京国债随时间存在上升趋势。在2006年之前，北京国债负担率小于0.0675，转换函数处于低区制向高区制转换的区间，此时反应系数处在下降区间。2007年之后，北京国债负担率超过0.0981，此时转换函数约等于1，反应系数约为0.1557，达到最低值。在2006年以前北京经济水平处于高速增长阶段，但由于初始经济发展水平较低，这一阶段北京的税负较轻，相应的国债负担也较轻，国债对经济增长的促进作用较强，但是随着北京经济水平的发展和税负的增加，2006年之后国债负担率超过0.0800，国债对私人投资的挤出效应明显，因此，国债对经济增长的促进作用下滑至最低值。

4.辽宁国债负担减轻，国债促进经济增长作用增强

自1998年起，辽宁国债总体呈现递减的趋势，相应的，2007年之前反应系数呈现递增状态，2008年之后基本持平，约等于0.7479。2000年之前辽宁国债负担率较大，超过0.0515，此时反应系数处于较低区间，国债对经济增长的促进作用较小。随着辽宁国债的减轻，反应系数显著增加，反应出低国债对经济增长的显著促进作用。随着国家经济结构调整转型，辽宁面临旧产业转型淘汰，经济增长缓慢，经济总量全国占比下滑的情况。这一时期辽宁的国债持续降低，较低的国债减轻了其对私人投资的挤出效应，因此，提升了国债对经济增长的促进作用。

综上可以看出，不论是高国债负担的省份还是低国债负担的省份，总体而言现阶段国债对经济增长具有显著的促进作用，但是，对于不同省份不同程度的国债负担，其对经济增长的促进作用呈现出显著差别。过高的国债负担使得国债的促进作用始终位于低区间，此时再增加国债负担，对于经济增长并无进一步的改善效果。较低的国债负担使得国债对经济增长的促进作用十分明显。

五、结论与政策建议

（一）结论

第一，在国家层面，国债对经济增长的促进作用处于低区间。

当国债负担率高于位置参数时，国债对经济增长仍然具有促进作用，但与转换变量小于位置参数的情况相比，其对经济增长的促进作用要小得多，即过重的国债负担会降低国债对经济增长的促进作用。因此，通过发行国债来促进经济增长的作用已大为弱化，重新评估和考虑适宜的国债规模已成为当务之急。

第二，在省际层面，国债对经济增长具有促进作用但各省差异较大。

不同省份、不同年份国债负担的不同阶段变化会导致国债负担率对GDP增长率的反应系数呈现出地区异质性和时变性。国债负担对上海经济增长的作用虽然仍是正向，但已进入最低值。低水平的国债负担对甘肃私人投资的挤出效应十分微弱，因此，国债对经济增长的促进作用始终处于最高值。随着北京经济水平的发展和税负增加，国债对经济增长的促进作用下滑至最低值。辽宁在早期以其较大的国债负担，带来较低的对经济增长的促进作用，随着辽宁经济总量全国占比下滑，较低的国债负担减轻了其对私人投资的挤出效应，因此，提升了国债对经济增长的促进作用。

（二）政策建议

第一，政府应控制国债规模。

从本文的经验分析结果来看，虽然国债对于经济增长一直保持促进作用，但是过重的国债负担使得政府投资支出对私人投资的挤出效应十分明显，降低了政府发行国债进行投资支出对经济增长的促进作用。因此，控制国债规模以减少挤出效应有利于保持国债对经济增长促进作用的最大化。

第二，调节税收以平衡国债在各省份之间作用的差异。

国债对各省份经济增长具有地区异质性和时变性，以上海和北京为代表的发达地区，其国债对经济增长虽然保持促进作用，但已经落入低区间。与此同时，以甘肃为代表的欠发达地区，国债对经济增长则具有显著的促进作用。因此，政府从全局出发，调节税收以平衡各省份国债负担，使其对经济增长促进作用保持在较高水平，对于发挥发达地区带头作用，平衡各地区经济发展具有重大意义。

参考文献：

[1] Kimbell，J.Y.，Mankiw，N.G. Consumption， Income， and Interest Rates： Reinterpreting the Time Series Evidence [R]. NBER Working Paper No. 2924，1989.

[2] Pelagids，T.，Desli，E.Deficits，Growth， and the Current Slowdown： What Role for Fiscal Policy？ [J] Journal of Post Keynesian Economics， 2004，26（3）：461-469.

[3] Gierner，A.， Kauermann，G.Sustainability of US Public Debt： Estimating Smoothing Spline Regressions [J] Economic Modelling， 2007， 24（2）：350-364.

[4] Panizza，U.， Presbitero，A.F.Public Debt and Economic Growth： Is There a Causal Effect？ [J] Mo.fi.r. Working Paper，2014，41（c） ：21-41.

[5] Forslund，K.，Lima，L.，Panizza，U.The Determinants of the Composition of Public Debt in Developing and Emerging Market Countries[J].Review of Development Finance，2011，1（3）：207-222.

[6] Borensztein，E.，Cowan，K.，Eichengreen，B.，et al.Prospects for Latin American Bond Markets：A Cross-Country View[M].Cambridge：MIT Press，2008.113-154.

[7] Eichengreen，B.，Luengnaruemitchai，P.Why Donesnt Asia Have Bigger Bond Market？ [R].NBER Working Paper，No.1057，2004.1-13.

[8] 劉溶沧，马拴友. 赤字、国债与经济增长关系的实证分析——兼评积极财政政策是否有挤出效应[J].经济研究，2001，（2）：13-19.

[9] 王维国，杨晓华.我国国债与经济增长关系的计量分析——兼论国债负担对国债经济增长效应的影响[J].中国管理科学，2006，（10）：300-305.

[10] 李戎，张珂玮，刘畅，等.国债规模与中国经济增长：基于省级面板的阈值固定效应分析[J].财政研究，2017，（4）：64-76+113.

[11] 高培勇.论举借国债的经济作用机制[J].经济研究，1996，（9）：26-31.

[12] 罗嗣红.我国财政赤字与国债挤出效应研究[J].中南财经政法大学学报，2003，（4）：60-64.

[13] 宋福铁.我国国债宏观经济效应的实证研究[J].郑州航空工业管理学院学报，2006，（4）：61-64.

[14] 杨文奇，李艳.国债挤出效应的实证分析[J].山西财经大学学报，2005，（3）：100-103.

[15] 陈共，类承曜.关于我国债务负担率及债务依存度的考察[J].财政研究，2002，（11）：2-6.

[16] 刘邦弛.国债理论限度与实践分析[J].财经科学，2001，（6）：79-82.

[17] Gonzalez，R.C.，Woods，R.E.，Eddins，S.L.数字图像处理：MATLAB版[M].阮秋琦译，北京：电子工业出版社， 2005.

（责任编辑：刘 艳）