燃料棒性能分析软件FRIPAC评估

张 斌，汪 洋，韦 俊，邓勇军

(中广核研究院有限公司，四川 成都 610042)

燃料棒作为反应堆内的第1道屏障，直接决定着整个电厂的安全性。我国压水堆核电厂堆芯系统设计[1]根据燃料棒在堆内的多种关键现象制定了相应的设计准则，包括内压准则、芯块中心温度准则、腐蚀准则、应变准则等，以规定燃料棒运行的性能要求。由于在反应堆运行过程中，燃料棒处于高温、高压、强中子辐射的恶劣工作环境中，且燃料芯块、包壳在功率水平及中子注量变化的情况下涉及到的物理、化学、热学和力学现象及其形成机理均非常复杂，无法直接观测或简单计算它们随功率和燃耗变化的情况，这更加剧了对燃料棒的综合性能进行预测分析的难度。对此，国际上通常利用燃料棒性能分析软件，通过建立一系列热学、力学模型对燃料芯块、包壳的堆内行为进行模拟，从而实现对燃料棒综合性能的预测。为解决我国燃料设计软件自主化问题，中广核研究院有限公司开发了燃料棒综合性能分析软件FRIPAC。

燃料棒性能分析软件在开发建模、评估、验证阶段，均需各类精确的实验数据以保证其计算模型的正确性与可靠性。国际上已开展了广泛的研究项目，在研究堆或商用堆中开展相关堆内实验来获取燃料棒相关辐照数据，如CIP(Cabri International Project)、HRP(Halden Reactor Project)、SCIP(Studsvik Cladding Integrity Project)等。其中，HRP是OECD/NEA(经济合作与发展组织核能署)下最大的国际核燃料联合研究项目，始于1958年，它主要基于挪威的Halden反应堆开展。HRP具有数据信息量大、实验过程严谨、实验数据准确的特点，从国外软件研发、验证及安全评审相关资料来看，目前HRP的实验数据已成为国际核燃料软件建模及验证的主要来源。目前，国际上较为广泛应用的燃料棒性能分析软件包括二维或准二维分析软件FRAPCON、PAD、FALCON、TRANSURANUS、FEMAXI及三维分析软件BISON、TOUTATIS、ALCYONE等，其中认可度较高的FRAPCON、TRANSURANUS、FALCON及BISON的验证与确认均采用Halden的实验数据[2-5]。

本文简单介绍FRIPAC软件的物理模型，通过与实验数据的对比对软件进行初步评估。

1 软件介绍

1.1 软件功能

FRIPAC适用于预测压水堆燃料棒在Ⅰ类工况(正常运行工况)、Ⅱ类工况(中频事故工况)下的性能，可分析的燃耗范围为0～62 GW·d/t(U)，芯块类型包括UO2、UO2-Gd2O3、MOX，包壳类型为Zr-4、ZIRLO。FRIPAC分析燃料棒在反应堆内辐照条件下的各方面行为，主要包括：1) 芯块/包壳温度分布；2) 芯块热膨胀、密实及肿胀；3) 包壳热膨胀、蠕变及辐照生长；4) 包壳应力与应变；5) 包壳腐蚀吸氢；6) 芯块-包壳相互作用(PCI)；7) 裂变气体释放；8) 燃料棒内压。

1.2 计算流程

由于燃料棒堆内热学、力学、辐照等行为耦合紧密，为准确模拟燃料棒堆内行为，需进行时间离散和空间离散。时间离散即对燃料棒辐照历史进行离散。空间离散即采用1.5维几何模型，先将燃料棒进行轴向分段，再对每个轴向段划分多个径向环进行一维径向分析，计算过程中不考虑轴向和方位角效应，以简化计算。

FRIPAC计算流程如图1所示。它包括两个基本循环(时间步循环和轴向段循环)以及两个迭代计算(间隙迭代与内压迭代)。两个循环的目的是为了实现软件的时间离散与空间离散，两个迭代计算的目的是实现热-力-核耦合分析并提高计算准确性。

2 理论模型

FRIPAC主要通过4部分模型来考虑燃料棒在堆内的不同现象：热学模型、力学模型、裂变气体释放模型和内压模型。

2.1 热学模型

热学模型主要用来进行燃料棒温度场的计算。在运行过程中，芯块内的裂变反应产生热量，这些热量通过芯块传热、间隙传热、包壳传热和对流换热过程传递到冷却剂中，如图2所示。燃料的温度变化主要受反应堆功率、材料特性(热导率、比热容、密度等)、燃料棒几何尺寸(间隙闭合与否)以及冷却剂流动特性(流量、密度)等因素的影响[6]。

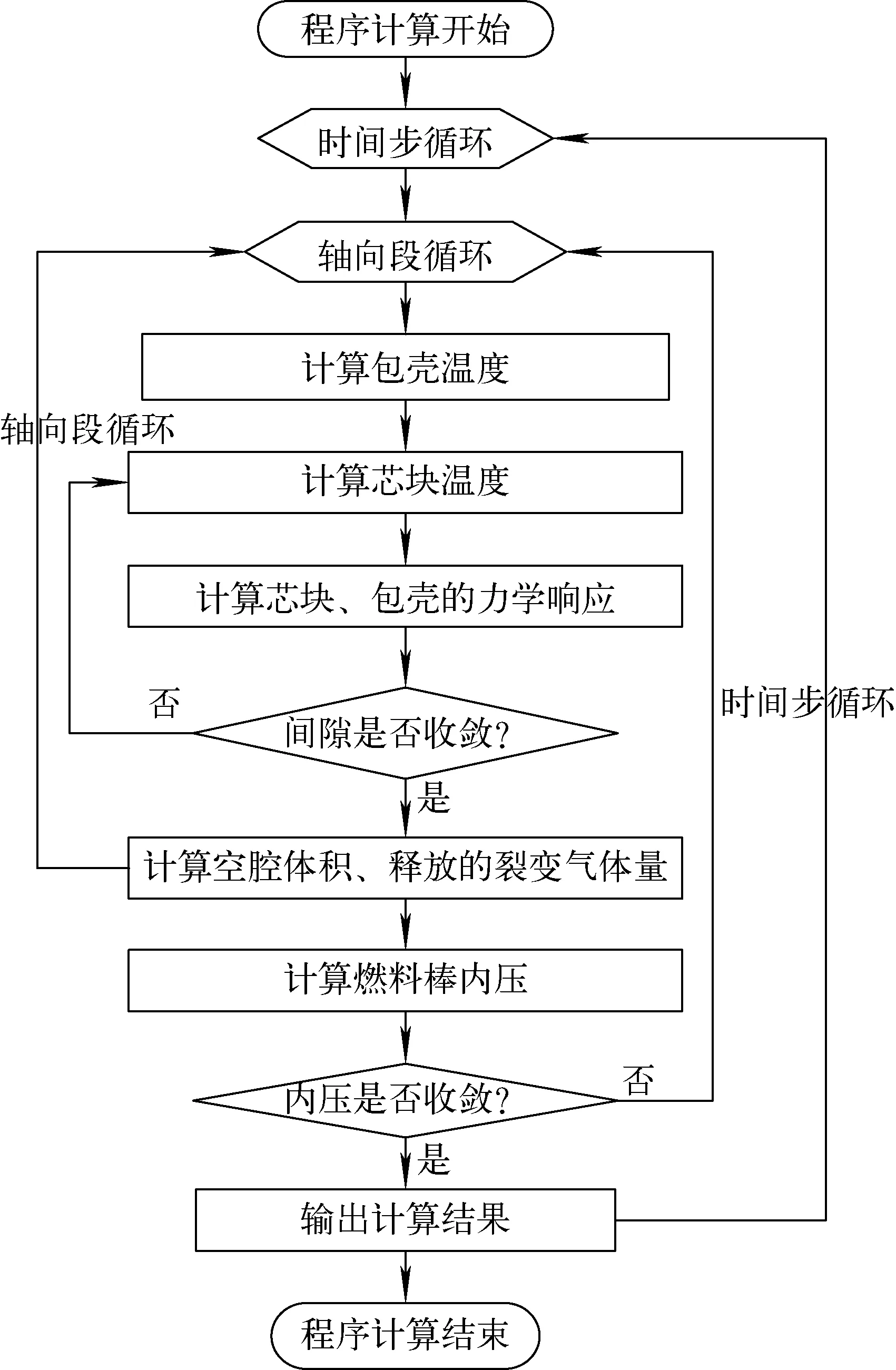
图1 FRIPAC计算流程Fig.1 Calculation flow of FRIPAC

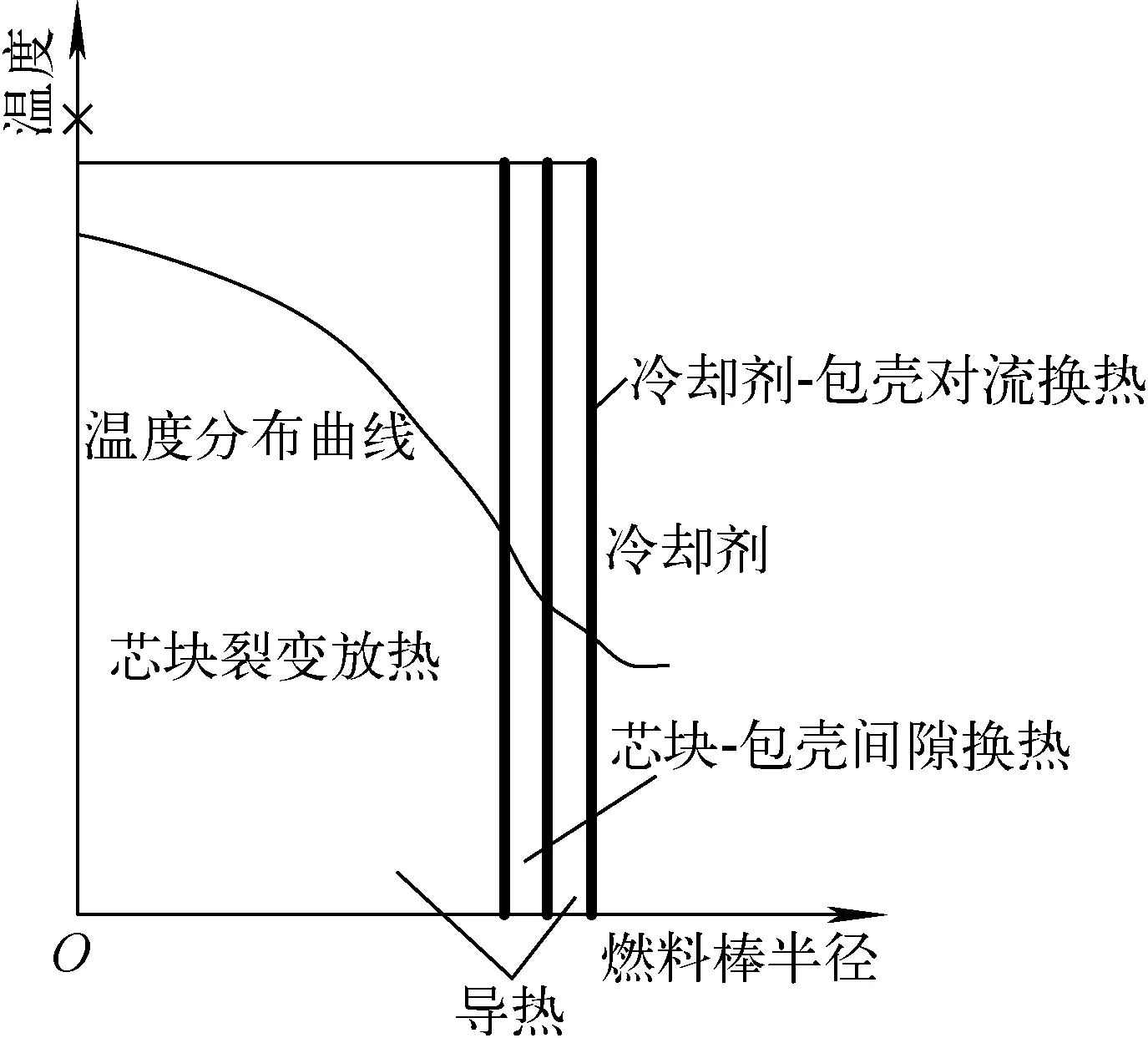
图2 燃料棒传热过程示意图Fig.2 Schematic of fuel rod heat transfer

FRIPAC热学模型分为4部分。

1) 冷却剂-包壳对流换热

通过冷却剂-包壳对流换热模型计算包壳外表面温度。在反应堆Ⅰ、Ⅱ类工况下，冷却剂-包壳对流换热包括两种模式：单相强迫对流换热和过冷核态沸腾换热。

在强迫对流情况下，采用Dittus-Boelter对流换热关系式[7]：

(1)

式中：hfilm为换热系数，W/(m2·K)；De为热力直径，m；K为冷却剂热导率，W/(m·K)。

在过冷泡核沸腾情况下，采用Jens-Lottes沸腾换热关系式：

TP2=Tsat+ΔTsat=Tsat+7.91e-p/62·q″0.25

(2)

式中：TP2为包壳外壁面温度，℃；Tsat为冷却剂饱和温度，℃；ΔTsat为沸腾换热温升，℃；q″为热流密度，W/m2；p为系统压力，MPa。

2) 包壳传热

燃料棒包壳传热模型利用基本传热方程计算包壳温度分布，不考虑包壳内部释热，忽略包壳轴向和切向的传热。包壳热导率为温度的一次函数：

λ=λ1+λ2T

(3)

最终依据传热基本方程(式(4))得到包壳内壁温度Tci：

(4)

(5)

式中：r为包壳径向尺寸，m；q′ 为功率密度，W/s；Dci、Dco分别为包壳内、外径，m。

3) 芯块-包壳间隙换热

芯块-包壳间隙换热用于计算间隙温升及芯块外表面温度，间隙换热包括3部分：气体导热、辐射换热和接触导热(芯块-包壳间隙闭合)。

ΔTgap=q″/hgap

(6)

式中：ΔTgap为芯块-包壳间隙温升，℃；hgap为间隙换热系数，W/(m2·℃)。

4) 芯块传热

我国城市马拉松与国外相比起步比较晚，美国波士顿马拉松开始于1897年，是全球首个城市马拉松比赛，中国最早开展马拉松的城市北京成功举办首届马拉松在1981年比美国晚了100多年。还有人们观念的滞后，越来越重的生活压力迫使人们把精力过多的放在了经济条件的改善方面，忽视了对身体和精神的充实。随着时代的发展、人们观念的更新，国家对体育越来越重视，同时也看到了体育给国民带来的好处，马拉松作为城市发展的一个载体，越来越受到有识之士的关注。国内各个城市国内有条件的城市可以加强有马拉松比赛经验城市的交流与合作，充分利用城市资源积极筹办马拉松赛。

燃料棒芯块传热模型同样基于基本传热方程，忽略芯块轴向和切向传热，但芯块传热模型需考虑芯块释热及芯块径向功率分布。

根据傅里叶定律，具有内热源的圆柱热传导模型[8]如下：

(7)

式中，qv为燃料棒功率密度。FRIPAC芯块热导率采用Halden模型[9]：

λ=1/(0.114 8+1.159 9Gd+0.004Bu+

2.475×10-4(1-0.003 33Bu)T+

0.013 2exp(0.001 88T))

(8)

式中：Gd为芯块Gd2O3的质量分数；T为芯块温度，K；Bu为局部燃耗，MW·d/kg(UO2)。

通常采用空间离散方法将芯块划分为多个径向环，求解式(7)即可得到芯块温度分布。

2.2 力学模型

燃料棒的力学行为会影响芯块和包壳的变形、芯块-包壳间的径向间隙尺寸及接触压力，进而影响燃料棒的温度分布和内压。FRIPAC的力学模型主要计算包壳及芯块尺寸变化，综合考虑芯块密实及肿胀、芯块热膨胀、包壳热膨胀、包壳蠕变等现象从而得到芯块及包壳径向尺寸、芯块-包壳间隙、接触压力等关键信息。

芯块力学模型主要考虑了芯块热膨胀、芯块密实及肿胀对芯块尺寸的影响：

teos=tbos(1+εth)(1+εsw)(1+εden)

(9)

式中：tbos、teos分别为时间步初与时间步末芯块径向环厚度；εth、εsw、εden分别为芯块热膨胀应变、芯块肿胀应变、芯块密实应变。

包壳弹性力学模型采用平面应变假设，轴向应变为常量。包壳受力变形满足3个基本方程：平衡微分方程、几何方程及物理方程，据此可推导得到欧拉方程：

(10)

结合包壳边界条件(式(11))求解式(10)可得到包壳位移关系式u(r)。

σr|r=Ro= -po，σr|r=Ri=-pi

(11)

式中：σr为包壳在半径r处的径向应力；Ro、Ri分别为包壳外壁、内壁半径；po、pi分别为包壳外壁、内壁压力。

2.3 裂变气体释放模型

燃料棒在运行过程中，由于裂变反应，芯块会不断地生成气体裂变产物和固体裂变产物。部分气体裂变产物将释放到燃料棒内部，这一过程称为裂变气体释放(FGR)。释放到燃料棒内的裂变气体将引起燃料棒内压升高，可能导致闭合的芯块包壳间隙重新打开，传热性能恶化，甚至发生包壳失效。通常，裂变气体释放现象分为两种情况：非热释放和热释放。非热释放主要是裂变气体由于击出和反冲现象，造成气体从芯块内部释放，通常使用经验关系式来考虑非热释放。热释放模型则依据扩散方程[10-11]得到：

(12)

式中：C为裂变气体浓度；D为裂变气体扩散系数；β为裂变气体的生成率；Δr为拉普拉斯算子；t为时间，s。

式(12)的边界条件为：

(13)

假设晶内气体在晶粒边界聚集，当晶粒边界气体浓度达到一定限制时开始释放，求解式(12)可得到每步的裂变气体释放率，进而求得对应的裂变气体释放量。

2.4 内压模型

在现有燃料棒分析软件中，内压大多采用理想气体状态方程。FRIPAC在具备此功能的基础上，使用更为接近真实情况的Peng-Robinson方程来分析燃料棒空腔内气体在高温、高压下的气体压力，降低了结果误差[12]。Peng-Robinson方程内压计算公式为：

(14)

式中：p为燃料棒内压，Pa；R为理想气体常数，R=8.314 J/(mol·K)；V为间隙气体体积，m3；a为内聚力参数；b为协体积参数[13]。a和b是混合气体温度与压力的函数。

3 初步评估

3.1 评估数据

本文采用HRP实验数据结合FRAPCON软件评估数据[2]，对FRIPAC进行初步评估，实验数据列于表1。表1中X表示该实验数据点是验证项。

3.2 温度评估

在燃料棒性能分析领域中，燃料温度会涉及到多方面模型，是众多模型耦合结果的产物，而芯块中心温度作为燃料温度中最具代表性、易表征的参数，它涉及冷却剂-包壳对流换热、包壳传热、包壳-芯块间隙换热、芯块传热等热学模型，所以它是确认燃料棒性能分析软件的准确性与可靠性的必要参数。另外，在实验过程中，芯块中心温度具备良好的可测量能力，目前国际中已积累不少与该参数有关的实验结果，所以通常使用芯块中心温度作为软件评估的参数。

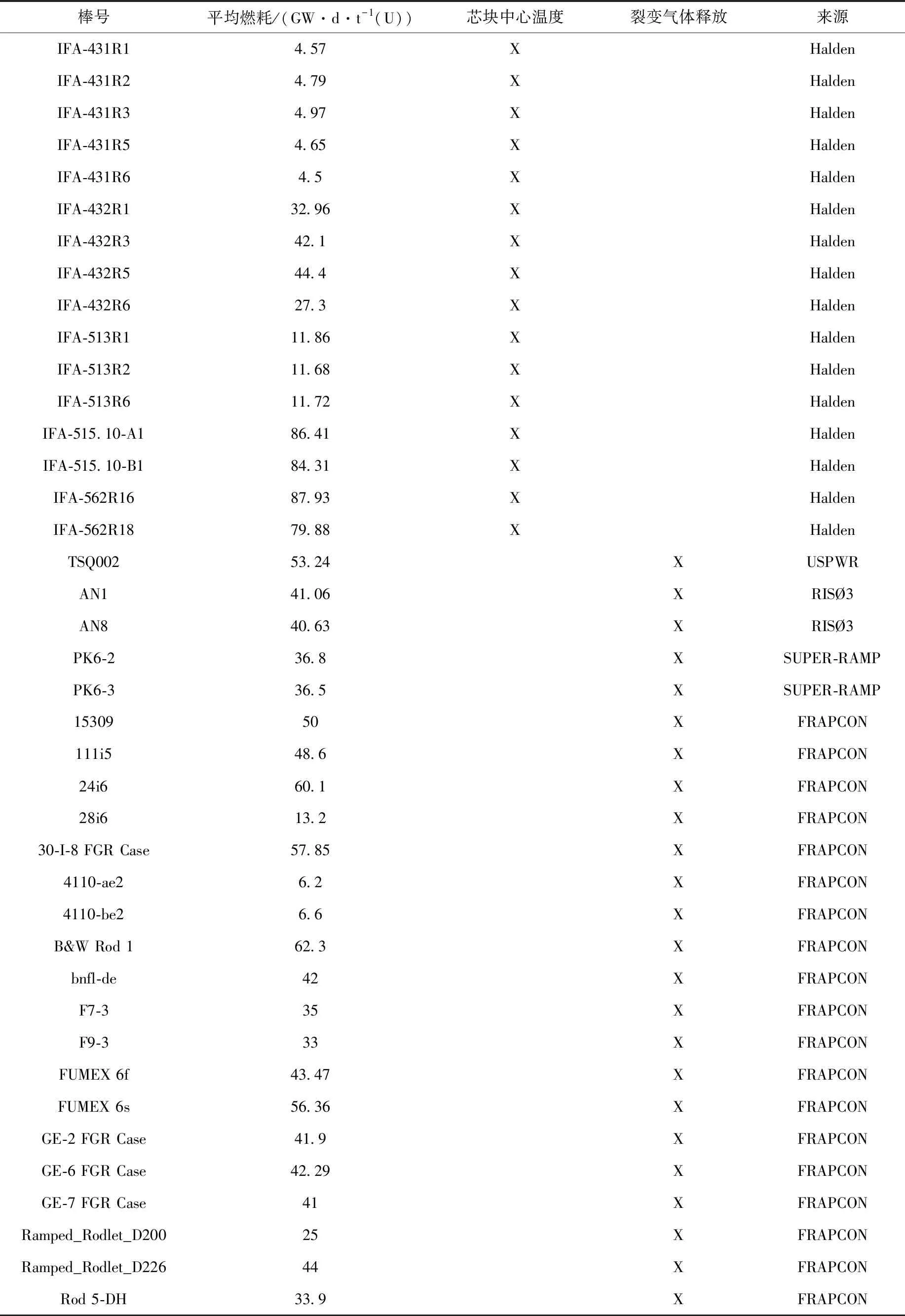
表1 用于FRIPAC初步评估的实验数据Table 1 Experimental data used for preliminary assessment of FRIPAC

本文基于Halden反应堆实验数据对燃料中心温度预测值(P)与测量值(M)进行了对比，结果如图3所示。本文初步评估采用了16根棒的实验数据，共约2 400个数据点，平均燃耗分布为4.5～88 GW·d/t(U)，P/M平均值为1.044，标准差σ为0.117，上下包络线为P/M=1±2σ。从图3可看出，FRIPAC对芯块中心温度的预测值与测量值符合较好。

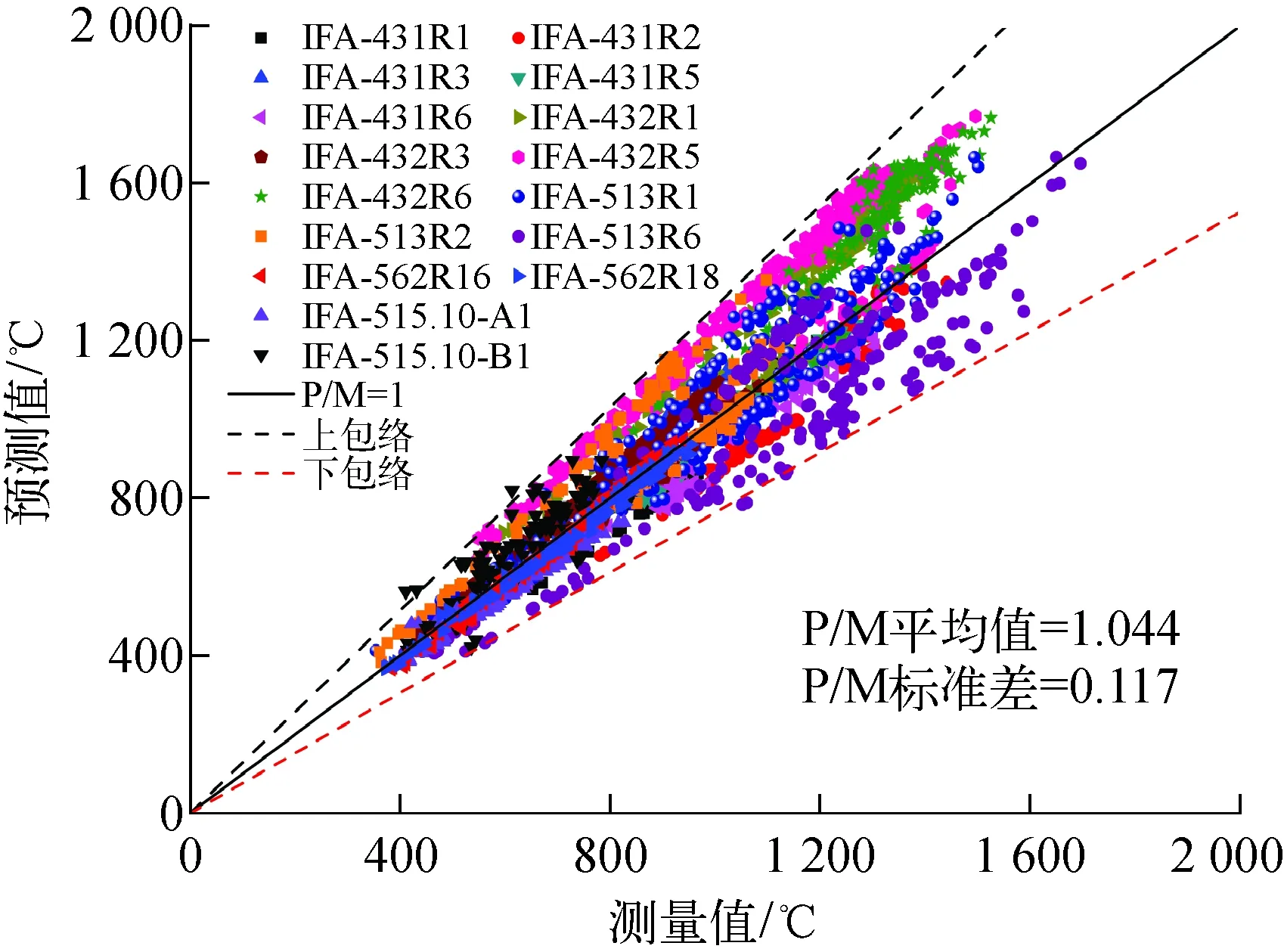
图3 芯块中心温度评估Fig.3 Assessment of pellet centerline temperature

3.3 裂变气体释放评估

裂变气体释放是燃料棒性能评估需要考虑的另一重要现象，尤其对高燃耗燃料更是如此。在辐照过程中，由U和Pu裂变产生的惰性气体会从燃料基体中释放到燃料棒的空腔中，这些气体在空腔中的累积将会降低燃料棒的导热性能并提高其内压，提高燃料棒破损的风险。因此，裂变气体释放的准确预测对燃料棒性能有着重大影响。

对FRIPAC裂变气体释放的评估基于24组裂变气体释放实验数据(表1)，裂变气体释放率的预测值与测量值对比如图4所示。P/M平均值为1.008 6，标准差为0.369 1，由此可见，FRIPAC对裂变气体释放率的预测值与测量值符合良好。

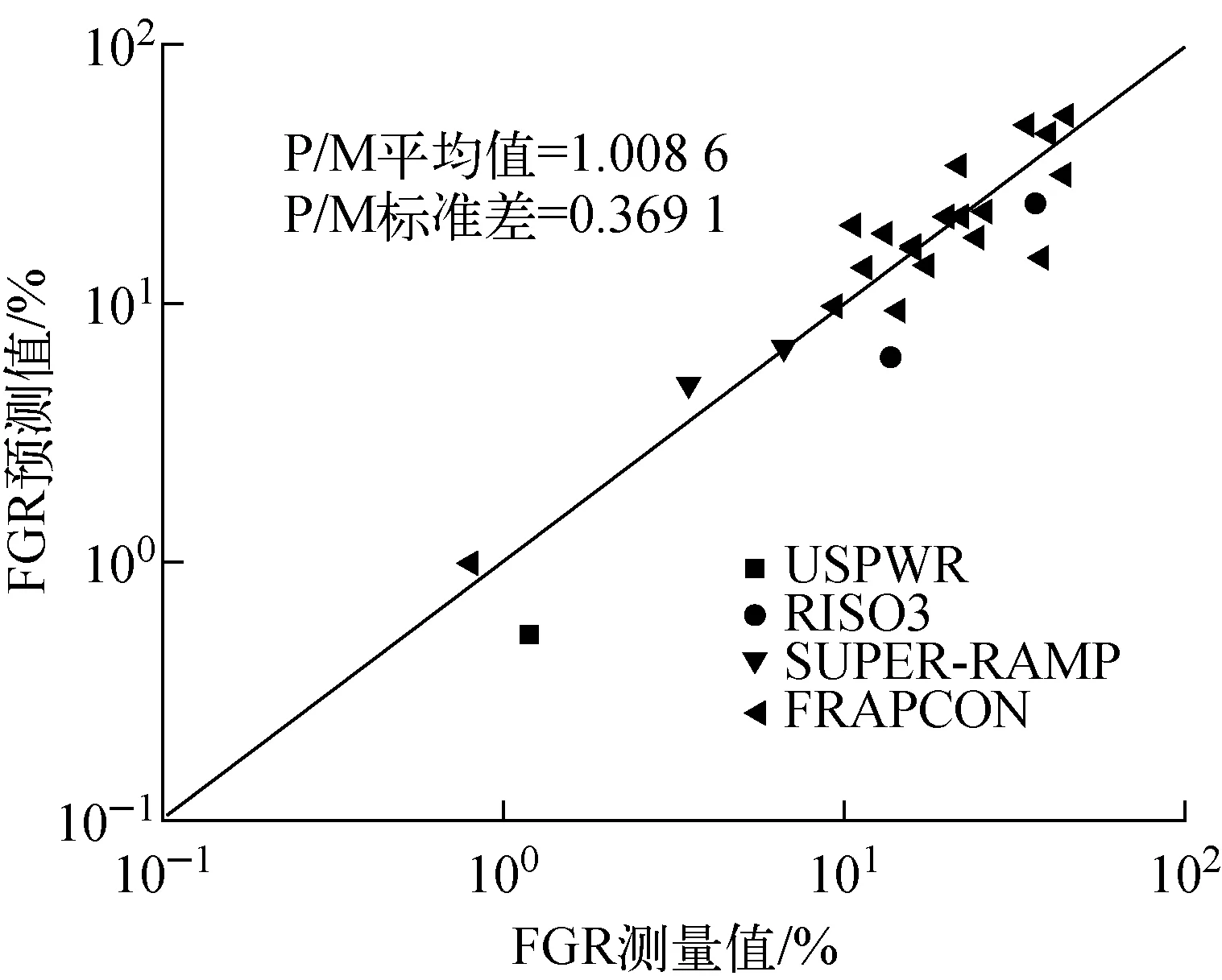
图4 裂变气体释放评估Fig.4 Assessment of fission gas release

4 结论

本文介绍了燃料棒性能分析软件FRIPAC的总体研发情况，对FRIPAC模型进行了简单描述，并与实验数据进行对比，对FRIPAC进行初步评估。评估结果表明，FRIPAC能准确预测燃料棒的芯块中心温度与裂变气体释放(包括高燃耗下燃料棒性能)，从较大程度上可认为FRIPAC计算结果是准确、可靠的，具备满足工程设计需求的潜力。

随着后续HRP实验数据梳理工作的完善，还将对FRIPAC进行更加全面的评估，并根据评估结果开展FRIPAC模型优化，提高软件的安全性与可靠性。