不同岩性下TBM滚刀破岩过程离散元分析

杨开新，蒋明镜,2,3,4,5，陈有亮，廖优斌

(1.上海理工大学 土木工程系,上海 200093；2.同济大学 土木工程防灾重点实验室,上海 200092；3.同济大学 岩土及地下工程教育部重点实验室,上海 200092；4.同济大学 地下建筑与工程系,上海 200092；5.天津大学 建筑工程学院,天津 300072)

1 研究背景

我国地势西高东低，呈阶梯状分布，山峦叠嶂的西部发展需要建设大批穿越复杂地质构造带的隧道工程。TBM在隧道开挖过程中不可避免地会遇到复杂岩层，而TBM刀盘上的滚刀受力不均容易导致倾覆、滚刀偏磨、刀圈断裂与开裂等一系列施工问题。为了使滚刀破岩过程在灾害最小和效率最高下进行，常常需要根据不同的地质条件不断调整滚刀断面参数及运行参数，而要实现这一过程，对于复杂岩层即不同岩性下滚刀破岩机理的研究就变得尤为重要。

Evans等[1]提出了盘形滚刀与岩石的相互作用理论。Nishimatsu[2]初步分析了滚刀破岩产生碎块的过程。Yang等[3]采用一点二角度模型推导出三维复合岩层破岩理论解，系统地分析了贯入深度、滚刀转速、岩层各向异性及上软下硬复合岩层倾斜度对破岩过程中滚刀法向力、破碎方式、破碎区域大小的影响。通过对滚刀受力的预测以及岩渣的形成进行理论解析，可以初步从宏观上认识滚刀破岩机理，但却不能有效地对破岩过程中内部微观信息的发展作出描述。

离散单元法[4](Discrete element method，DEM)因其能够很好地模拟岩层破裂及大变形问题并能从微观角度揭示其破坏机制，成为了滚刀破岩机理研究常用有效的方法。Gong等[5-7]建立了双把TBM刀具侵入花岗岩的离散元模型,分析了节理间距与节理倾角对破岩过程的影响。Huang等[8]分析了滚刀侵入岩层过程，发现临界贯入深度与特征长度有关。Jiang等[9]采用PFC2D模拟了完整和节理岩层的双滚刀破岩过程，分析了不同节理倾角、间距下的最优刀距，并从微观角度解释其机理。另外，谭青等[10-14 ]采用PFC2D系统地模拟了TBM滚刀破岩过程。研究了球齿形、盘形滚刀的破岩机理并且较为全面地分析了破岩中的影响因素。孙亚[15]将基于微观胶结试验得到的岩石微观力学模型[16-17]植入PFC软件，通过陈贺[18]所做试验得到的无厚度胶结强度包络面标定了Lac du Bonnet花岗岩，模拟了单滚刀侵入单一完整岩层、双滚刀侵入简单节理岩层的破岩过程，较为系统地研究了不同影响因素对滚刀破岩效率的影响。蒋明镜等[19]模拟了滚刀破岩过程并且重点分析了滚刀破岩的各阶段的宏微观机理。然而实际工程中，TBM滚刀常遇到复杂岩层，对于不同岩性差异下滚刀破岩机理的研究，不仅为复杂岩性下的滚刀破岩机理的研究提供了指导价值，更是复合岩层下滚刀破岩的研究基础。为此本文采用离散单元法，于PFC2D商业软件中植入考虑胶结尺寸的微观接触模型[16-17]，该模型能够考虑岩石颗粒之间的胶结尺寸对强度包络线的影响，更加符合岩体材料的真实破坏特性。通过研究不同岩性与滚刀刃数对于破岩效率的影响，力图揭示其宏微观机制，分析其内在破岩机理。

2 模型介绍

本文对岩石宏观参数进行选定时，通过对不同岩性的单轴抗压强度之间设置一定的梯度差，来标定具有一定代表性的岩性[20],本文选用的软硬岩如表1所示。

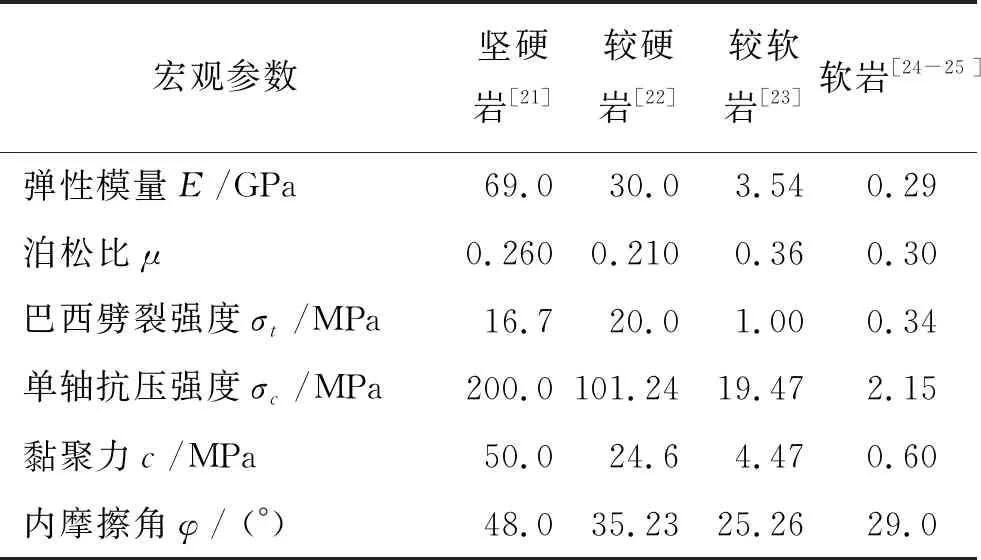
表1 本文数值模拟所需的岩石宏观参数

对本文的岩石微观接触模型参数进行标定，标定的具体步骤如下：(1)先采用分层欠压法[26]成样，通过分层欠压法能够制备相对均匀的试样，其中单轴压缩试样和双轴压缩试样都采用宽高比为1∶2的长方形试样，包含10 000颗粒；而巴西劈裂试样采用正方形试样，包含20 000万颗粒。其中采用能够较为准确合理地反映岩石类材料的颗粒级配[18]，如图1示。该级配共有15种粒径，最大粒径是2.0 mm，最小粒径是0.5 mm，平均粒径是1.3 mm，不均匀系数是2.4，曲率系数是1.1。(2)对试样进行预压形成初始地应力。(3)加模型参数形成岩石试样。(4)将岩石试样切削成可加载的试样。(5)加载试样得到相应的力学指标。通过对单轴压缩试样进行加载得到单轴抗压强度、弹性模量和泊松比；通过对巴西劈裂试样进行加载得到巴西劈裂的峰值强度，换算得到单轴抗拉强度值。通过对双轴压缩试样进行加载得到不同围压条件下的峰值抗压强度，并计算得到内摩擦角和黏聚力。经过不断地调整模型微观参数，直到离散元试样的宏观力学特性和试验的宏观力学特性目标值相匹配，并在误差许可范围内。经细心的选取，最终标定的微观参数如表2所示。

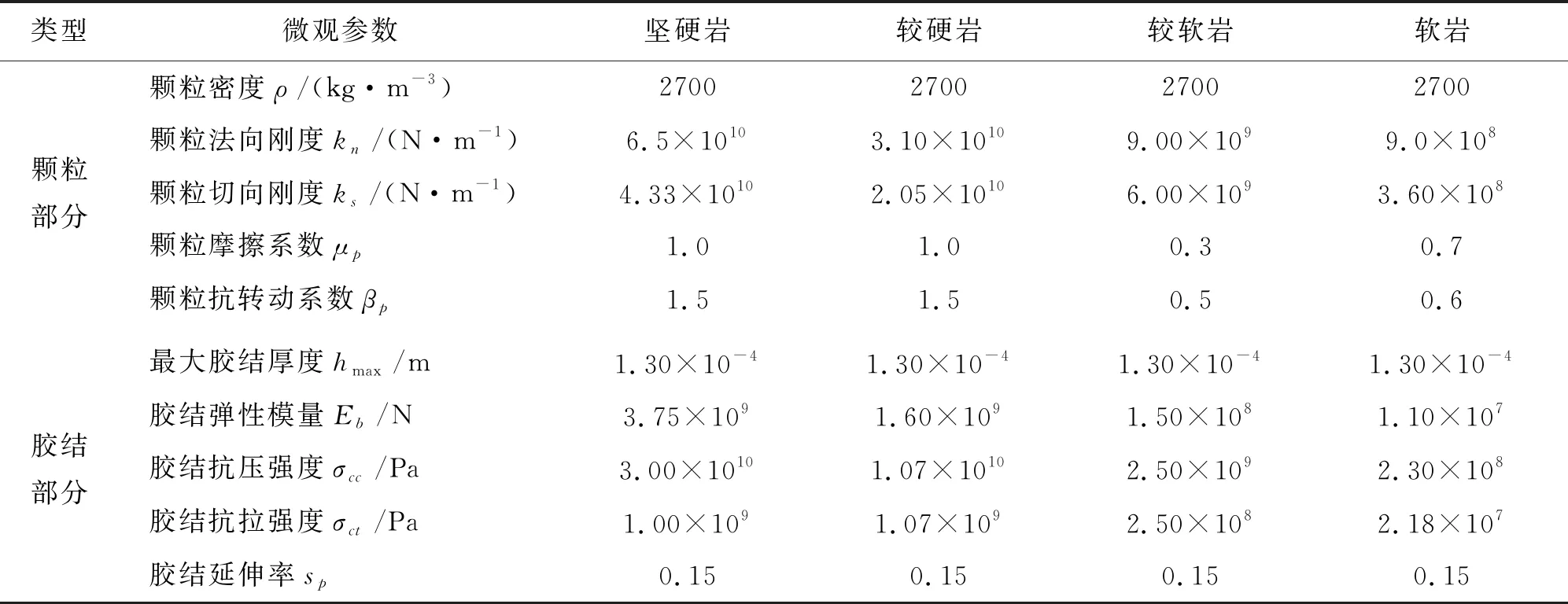
表2 DEM模拟的岩样微观参数

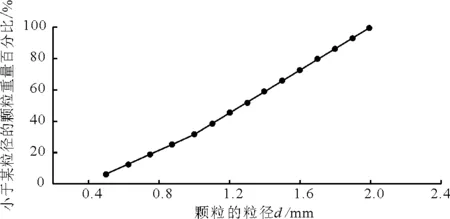
图1 DEM岩石试样的颗粒级配曲线[18]

3 滚刀破岩数值模拟

3.1 刀具及破岩模型

刀具消耗费用与换刀所消耗的时间是实际工程施工不可忽视的因素，而安装在刀盘上的滚刀是TBM的关键部件和易损部件。如图2所示，取单个滚刀受力分析可得到由刀盘推力提供的法向力、由刀盘扭矩提供的滚动力及刀盘旋转产生的切向力，一般认为，在掘进过程中法向推力是破岩的主要因素，而滚动力的影响很小[27]，因此本文模拟了二维的滚刀侵入岩层的过程。刀盘上滚刀设计参数主要有滚刀间距S、贯入深度D、滚刀刃角α、滚刀刃宽w，采用施工中运用比较广泛的常截面盘形滚刀，模拟中滚刀刃宽w=15 mm、刃角α=60°、滚刀间距S=100 mm固定不变，重点研究滚刀数目和不同岩性对破岩的影响。模拟的滚刀采用PFC5.0软件中的墙命令生成，单个滚刀采用六面独立的墙体闭合围成，整个破岩过程中认为是刚性的，墙体的法向刚度和切向刚度比颗粒刚度略大即可，颗粒与墙之间的摩擦系数取为零。

本文研究了研究4种岩性下单滚刀、双滚刀、三滚刀的破岩机理，以较硬岩为例，破岩示意图如图3所示。根据袁聚云等[28]的研究，当滚刀刃宽与岩石试样宽度的比值小于0.02时，可以有效地减少滚刀破岩过程中的尺寸效应。因此本文选取的试样尺寸为760 mm×380 mm，颗粒数目约30×104，试样孔隙比为0.2。

3.2 破岩阻力与侵深关系分析

本文模拟了4种岩性下不同滚刀刃数的破岩过程，其中选取较硬岩作为对照组，探究不同岩性与滚刀刃数下的破岩机理。推力-侵深曲线是滚刀侵入岩层的基本关系曲线，如图4所示。根据推力-侵深曲线特征可以将不同刃数下的滚刀破岩过程分为3个阶段：加载阶段、卸载阶段和残余跃进阶段。加载阶段滚刀推力基本随着侵入深度呈现线性增加，直至推力峰值；卸载阶段达到峰值阶段，滚刀推力会迅速跌落至较小的值，这对应于滚刀前方岩层破碎，滚刀受到的阻力瞬间减小，刀头会出现短暂的临空现象，甚至有可能产生刀头瞬间脱落的危害；残余跃进阶段，破岩阻力随着滚刀的侵入深度波动，这是由岩层破碎引起的残余跃进，这种波动常常伴随一个稳定值，此时对应的胶结破坏点增幅减小趋于稳定，说明了滚刀行进的阻力在不断减小，并且此时岩层内部裂纹很难产生，试样已经破坏。此外，随着滚刀刃数的增加，多滚刀的推力-侵深曲线与单个滚刀作用的曲线一致性较好。从不同刀刃数的胶结破坏数分析看，本文的胶结破坏主要分为两种，拉剪破坏和压剪破坏。在加载阶段产生的胶结破坏数较小，裂缝开始形成；到了卸载阶段，裂缝不断发育、扩展，此时胶结破坏数增加较为明显；而到了残余跃进阶段，裂缝已发育完全，岩石试样已破坏，胶结破坏数达到稳定水平。综上所述，胶结破坏数的发展与峰值推力变化阶段是宏、微观的相互对应，且拉剪破坏产生胶结破坏数发展规律与压剪破坏的规律一致性较好。

图2 全断面掘进机刀盘及滚刀示意图

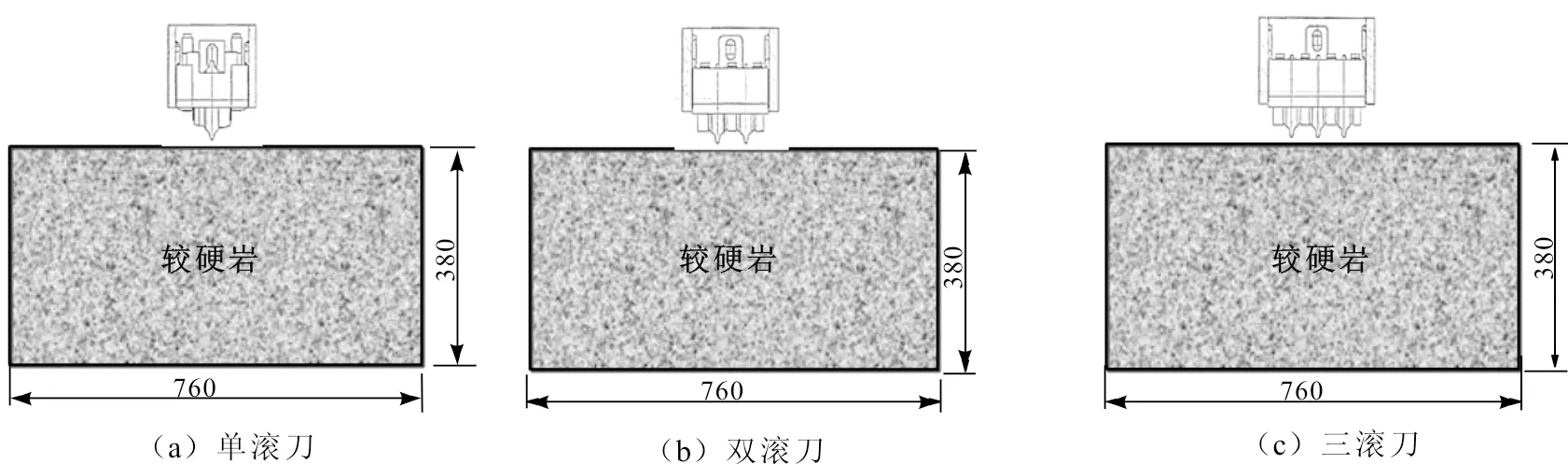
图3 3种滚刀刃数下滚刀破岩模型图(单位：mm)

图4 多刃滚刀破较硬岩层的推力-侵深关系曲线图

3.3 裂纹扩展机理分析

图5为较硬岩单滚刀、双滚刀与三滚刀不同贯入度下的力链分布图，图5中的线条粗细表示接触力的大小，接触力越大，线条越粗，力链越密。由图5可见，贯入度为1 mm时出现Sanio[29]所提及的静水压力核，部分力链与集中区域散射出的力链互相垂直呈现弧形分布，这与Moon等[30]所做实验观察到的现象一致。图5(c)左下方出现局部区域力链阻断，主要是因为崩碎的块体与母体已经没有接触，故无法传递力，该贯入度下的应力水平很低，达到了残余跃进状态，此时破岩不需要太多的能量。图5(e)双滚刀作用下力链分布对称，受力传递路径比较清晰均匀。图5(g)中左右两把滚刀受力出现不均匀，主要是因为岩层产生了破碎区，这与单滚刀时的情况是一致的。由图5(i)可知，三滚刀作用时力链分布广而密，整个试样主要受到压应力，可以观察到，此时较硬岩还是处于弹性阶段，出现3个力链核，受力比较清晰；图5(j)较硬岩力链发展没有较大的变化，但单个滚刀作用下方接触力链更为浓密；对于图5(k)，滚刀下方刚刚出现岩层破碎区域，接触力链呈现了不对称分布的特征，表现为右侧大而左侧小的核状，主要是因为左侧滚刀下方岩层破碎区域大，导致了左侧滚刀出现了滚刀临空区域，而右侧的滚刀则还处于受力集中区域。

图5 较硬岩单滚刀、双滚刀与三滚刀不同贯入度下力链分布图

选取了不同滚刀刃数与岩性下的破岩宏观局部图，如图6所示。其中图6(a)～6(d)为单滚刀、图6(e)～6(h)为双滚刀、图6(i)～6(l)为三滚刀情况下4种岩性的破岩局部示意图。

由图6(a)～6(d)可知岩层的破坏模式主要可以分为两大类：块状剥落类和碎渣剥落类。其中坚硬岩、较硬岩和较软岩岩层可以明显看出滚刀左右侧有较大的岩块已剥落，而软岩则出现众多微小裂缝，表面碎渣剥离母体，伴随着飞溅的岩渣。观察图6(e)～6(h)，发现4种岩性的岩层都出现了双滚刀之间的贯通裂隙，越硬的岩层的破岩容易停留在表层，形成表裂缝和斜裂缝；中等岩性的岩层易形成较长的贯通裂缝；而软岩则易形成呈表面的崩碎状、容易发展的纵向裂缝和中裂缝。通过图6(i)～6(l)可知，三滚刀的破岩模式主要分两种类型：破碎区贯通型和破碎区非贯通型。坚硬岩或软岩都较容易形成破碎区贯通，坚硬岩呈现块状贯通脱落而软岩出现颗粒崩碎状贯通。对于介于之间的岩石则更倾向形成破碎区非贯通，主要是因为中间岩性的岩层既没有坚硬岩由于高强度形成的完整性使得裂缝相互贯通，也无法像软岩一样形成表层的小裂隙实现贯通，只能形成一定体积的破碎，而这些破碎的岩渣在未达到相互贯通之前已经与自由面贯通而形成块体剥落。

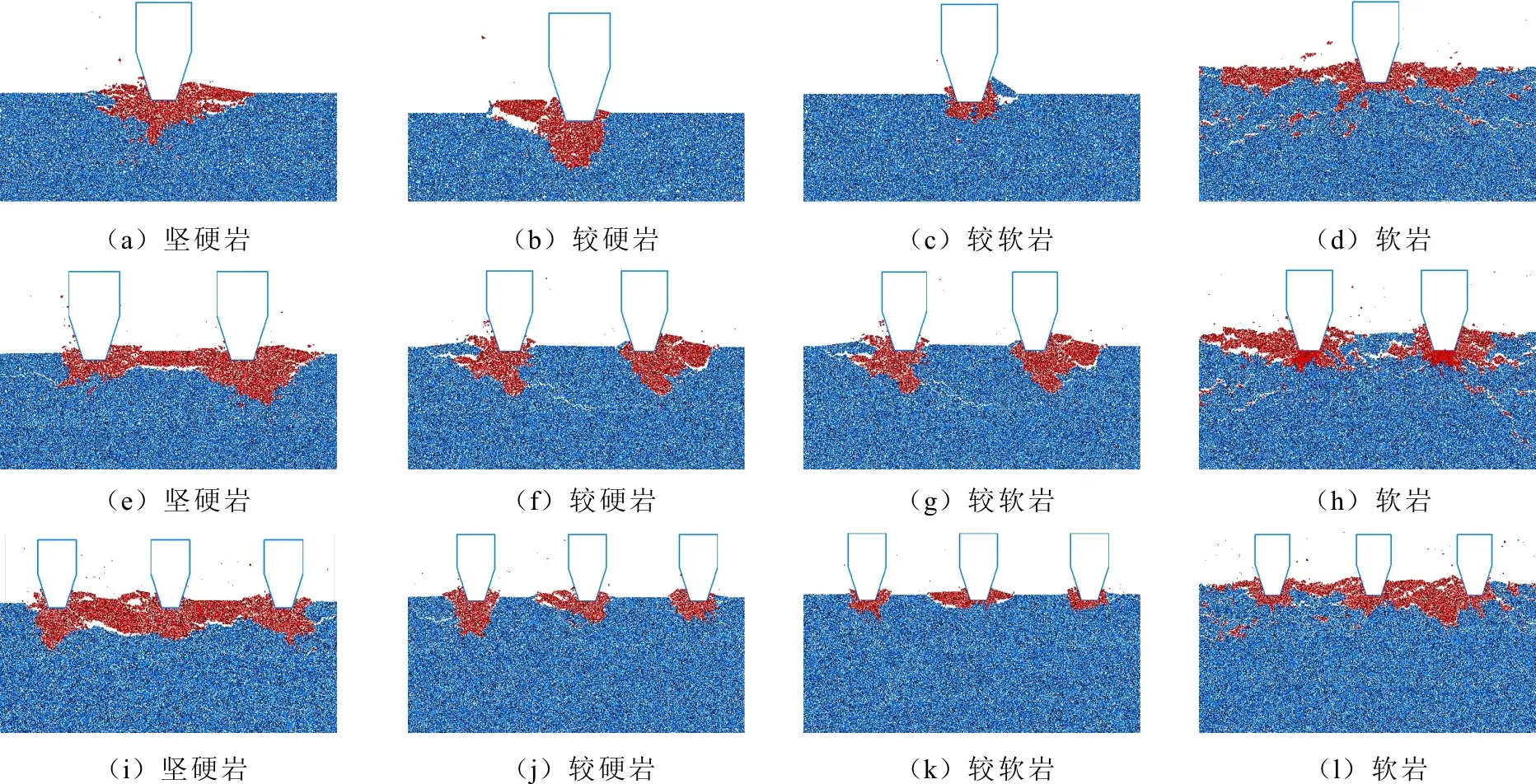
图6 不同滚刀刃数下不同硬度岩层破岩局部示意图

3.4 结果讨论与分析

图7(a)为不同滚刀刃数的破岩过程中的胶结破坏数目。胶结破坏总数从微观角度上描述了破岩能力，胶结破坏数目越大，表明滚刀的破岩能力越强。对于坚硬岩和较硬岩可知，胶结破坏数目随着滚刀刃数的增加而增加，表明破此类硬岩，通过增加滚刀刃数能够有效提高破岩能力。但对于较软岩而言，从单滚刀升到双滚刀破岩能力是升高了，但从双滚刀升到三滚刀破岩能力没增加反而减小了，这可能是因为低强度的岩层由于两侧滚刀的侧压力施加给中间滚刀正下方的岩层形成了一定的束桶作用，导致中间岩层强度在一定程度得到了提高。另外，Jiang等[9]采用了胶结破坏比能耗作为评价破岩效率的一个重要指标，这是对传统室内试验定义滚刀破岩效率的“比能”的一个重要补充。其中胶结破坏比能耗的定义为：破岩过程中滚刀所消耗的能量和滚刀作用下产生的胶结破坏点总数的比值。胶结破坏比能耗从微观的角度解释了由于单个胶结破坏产生微小裂隙所消耗的能量，这能够在一定程度上表征破岩过程中破岩效率，并且胶结破坏比能耗越低，破岩效率越高。

图7(b)给出了不同岩性下3类滚刀破岩时胶结破坏比能耗变化规律。其中滚刀破岩所消耗的能量通过荷载-侵深曲线积分得到，而胶结破坏总数都统一取了贯入度为5mm时胶结破坏点的总数的稳定值。由图7(b)可知，对于坚硬岩采用三滚刀时破岩效率最高，对于较硬岩、较软岩和软岩则采用单滚刀时破岩效率最高。

图7 不同岩层下三类滚刀破岩胶结破坏分析

图8峰值法向推力 图9比能耗与岩石单轴抗压强度关系曲线

图8为三类滚刀破岩时滚刀所受到的峰值法向推力。在破较软岩与软岩时，3类滚刀的峰值法向推力差异较小；而对于坚硬岩与较硬岩时，双滚刀与三滚刀会出现左右滚刀峰值法向推力相差较大，主要是因为破岩进入峰值阶段不一致，导致破岩过程中常常会出现一侧滚刀正下方岩层先破碎，而另外一侧滚刀达到峰值前就已经因为岩层出现破碎而导致推力跌落。这正是离散元模拟滚刀破岩的一大优势，能够很自然地模拟破岩过程中的渐近破坏。另外，对于3类滚刀，岩性的差异对峰值法向推力的影响是巨大的，这与工程实践明显是一致的。

根据谭青等[31]采用的不同岩性的岩石滚刀切削试验，试验中的岩石为花岗岩、板岩、砂岩、石灰华与混凝土，其中对应了坚硬岩、较硬岩、较软岩和软岩。通过试验中单滚刀切割干燥岩石所得破岩比能耗数据，建立单滚刀破岩比能耗与岩石单轴抗压强度的关系曲线，与本文单滚刀情况下不同岩性的胶结破坏比能耗对比，如图9所示。在岩石单轴抗压强度小于100 MPa时，破岩比能耗随着单轴抗压强度增加而增加，这与胶结破坏比能耗的趋势一致性较好，说明在较低岩石单轴抗压强度下，胶结破坏比能耗是可以作为评价破岩效率的一个指标。但当强度超过100 MPa时，试验中出现较大跌落，这与模拟区别明显。主要是因为不是所有的微观裂隙都能发展成破岩所需要的宏观裂缝，有些微小裂隙还可能出现闭合现象，没有形成主裂纹的胶结破坏在破岩过程的贡献是微小的，只是在一定程度上削弱了岩层。举例来说，做功不变时，当破岩过程中有大块的岩渣掉落时，所需要的胶结破坏数目可能不需要很多，但在工程上此时破岩效率是较高的，而微观上胶结破坏数目越少，破岩效率越低，这与图9中轴压超过100 MPa时曲线走势是一致的，这说明了采用胶结破坏比能耗尽管在一定程度上能够描述破岩效率，但还是存在缺陷。

4 结 论

本文通过离散单元法，采用基于室内试验提取的考虑胶结尺寸的岩石微观胶结接触模型，模拟了不同滚刀刃数下侵入4种单一岩性岩石的过程。主要研究结果表明：

(1)通过模拟单滚刀、双滚刀及三滚刀侵入4种不同岩性岩石的破岩过程，发现不同刃数的滚刀破岩过程均可以分为3个阶段：加载阶段、卸载阶段及残余跃进阶段。

(2)胶结破坏类型主要分为两种：拉剪破坏和压剪破坏。对于坚硬岩和较硬岩，胶结破坏数目随着滚刀刃数的增加而增加，但对于较软岩和软岩而言，增加滚刀刃数并不能增加胶结破坏数目。

(3)破岩过程中滚刀受到的阻力可以用峰值法向推力表示，阻力与岩性密切相关，岩石单轴抗压强度越大，破岩时的阻力也越大。

(4)采用胶结破岩比能耗来评价破岩效率，其中对于坚硬岩，三滚刀的破岩效率最高，而对于较硬岩、较软岩和软岩，采用单滚刀破岩效率更高。