基于环境变量的海洋浮标抗风等级计算

费梓凡，王普慈，赵 强

(1.上海市进才中学，上海 200135；2.宁波市海洋环境监测中心，浙江宁波 315012；3.卫星海洋环境动力学国家重点实验室，浙江杭州 310012)

海洋浮标（以下简称浮标）是一种布放在特定海域的观测装备，常用于风、浪、流、海温等海洋气象要素的定点观测，具有全天候、全天时收集海洋环境资料的能力，根据外形可将其分为圆盘形，柱形，船形和球形浮标等。与传统的船载观测相比，浮标的观测周期更长（通常以月和年为单位），而与卫星遥感观测相比，浮标的观测频次更高（通常可做到小时级至分钟级），且较少受到天气系统的影响，是现代海洋环境立体观测系统的重要组成部分[1，2]。

浮标系统通常由浮在海面的浮体部分和位于海底的锚系部分组成。浮体在海上由于受到风、浪、流的影响，不可避免的会发生摇摆、移动，严重时会拖拽锚系离开原先的位置，称为走锚。为了避免浮标在不利天气条件下（如台风）发生走锚，在浮标系统布放设计及维护时，需要对浮标在特点环境下的受力及泊稳条件进行分析计算。国内外学者通常采用静力模型或动力模型对浮标的风、浪、流载荷进行受力分析[3-7]。缪泉明等[3]利用三维势流理论及卡明斯六自由度运动方程对极限海况下两个水深的三锚系统的圆盘浮标运动及锚链受力进行了数值模拟估算。聂孟喜等[4]在时域内建立了一种计算防风水鼓系泊系统在风、浪、流联合作用下系泊力的方法，计算结果与经验公式计算结果吻合较好。肖越等[5]利用数值方法在频域内研究了锚泊浮体在风、浪、流联合作用下的运动及锚链张力，并对一锚泊半潜平台进行了实际校核。刘愉强等[6]探讨了浮标标体受到风、浪、流联合作用时的受力分析计算方法，编写了一套计算浮体受力程序，为实际浮标锚系设计、配置提供依据。张继明等[7]建立了浮标锚泊系统的运动方程，提出了在海洋环境中作用在浮标及锚系上的各种外载荷的计算方法，得到了浮标的运动方程以及锚系的受力表达式。

刘愉强等[6]在探讨海洋浮标标体受力时考虑了较为完整的风、浪、流作用，且已在南海深海海域进行了实际应用检验。本文以其工作为基础，修改了浮体波浪受力部分的计算公式，增加了锚系部分的受力分析，给出了浮标泊稳条件，使之也适用于近岸海洋浮标的受力计算，并采用Python编程语言编写了一套浮标抗风等级计算的程序，用于特定浮标系统所能抵御的最大风级以及特定风级下浮标系统泊稳所需的最小锚重的计算，可为海洋浮标的布放设计和维护提供参考依据。

1 浮标受力分析

1.1 浮标浮体受力分析

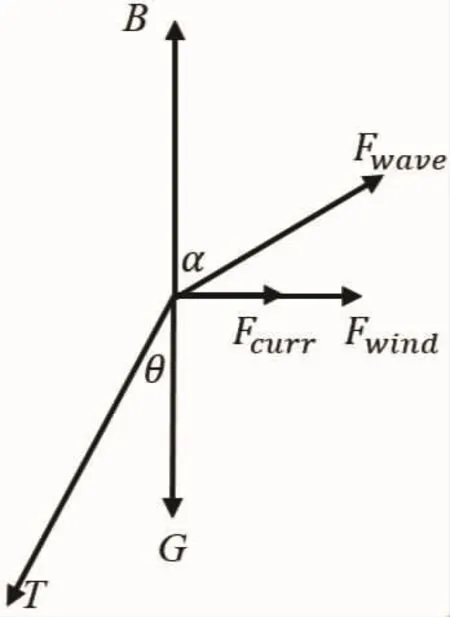
图1 浮标浮体的受力分析Fig.1 Force analysis of a floating body

浮标浮体漂浮在海面，除受到自身的重力和海水的浮力外，还会受到锚系对浮体的拉力，以及海风、海流和海浪的作用。其中，海风和海流在水平方向上的运动幅度远远大于在垂直方向上的运动幅度，其作用可以看做只在水平方向上存在；而海浪在水平和垂直两个方向都存在显著的运动，因此海浪对浮体的作用也存在于这两个方向上。在平衡条件下，浮体的受力（图1）可以写为[7]：

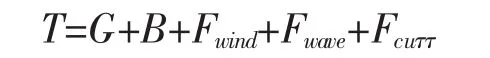
式中，T表示锚系对浮体的拉力；G表示浮体的重力；B表示浮力，Fwind、Fwave和 Fcuττ分别表示风、浪、流对浮体的作用力。

1.1.1 风的作用力

风对浮体的作用力一般采用风压与受力面积的乘积计算，

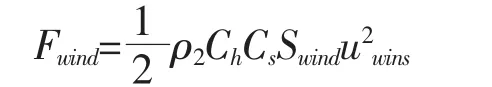
式中，ρ2为空气密度，取1.2 kg·m-3；Ch和Cs分别为浮体的高度系数和形状系数，其取值参考《海上移动平台入级规范 2016》[8]，分别取 1.0 和 0.5；Swind为风受力面积（单位 m2），不考虑浮体的倾斜，即为浮体位于水面之上部分的中线纵向截面；uwins为水平风速（单位m·s-1）。将各参数带入上式，风的作用力可简化为：

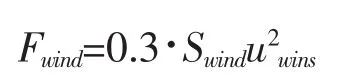
1.1.2 流的作用力

与风的作用相似，流对浮体的作用力可以写为：

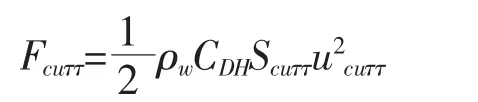
式中，ρw为海水密度，一般取 1 020 kg·m-3；CDH为水平阻力系数，默认取 0.5；Scuττ为流受力面积（单位m2），即浮体位于水面之下部分的中线纵向截面；ucuττ为海流流速（单位m·s-1）。将各参数代入上式，流的作用力可简化为：

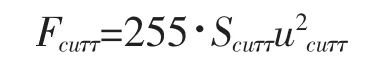
1.1.3 浪的作用力

本文选用艾立波理论计算波浪对浮体的作用力。艾立波理论，又称线性波理论或正弦波理论，其波形为正弦曲线，适用于微幅波，即波高H与波长L及水深d相比甚小的波浪。在不利天气条件下，近海波高H一般小于10 m[9]，而波长L通常在100 m左右[10]，属于微幅波，且实践表明，在许多实际问题中，尽管实际波况已超出微幅波条件，但用此种理论进行工程计算也能有较好的效果，因此在工程实践中，尤其在作初步的估算时，艾里波理论仍得到广泛的应用[11]。

根据艾立波理论，波浪对浮体的作用力在水平方向上和垂直方向上可分别写为[6]，

其中，Vb为浮体湿水体积（单位m3）；CiH和CiV分别为水平惯性力系数和垂直惯性力系数；u和v分别为波浪水质点的水平速度和垂直速度（单位 m·s-1）；u˙和v˙分别为波浪水质点的加速度（单位 m·s-2）；CDH和CDV分别为水平阻力系数和垂直阻力系数；SwaveH和SwaveV分别为浮体的水平迎浪面积和垂直迎浪面积（单位m2）。式中第一项是由波浪加速度产生的力，与浮标的体积和加速度有关；第二项是由于水的惯性引起的附加质量力，其表达形式与风、流的作用力相似，大小与波浪质点的速度和浮标的受力面积有关。

线性波的波面（η）、波长（L）、速度（u、v）和加速度（u˙、v˙）可表示为[6]：

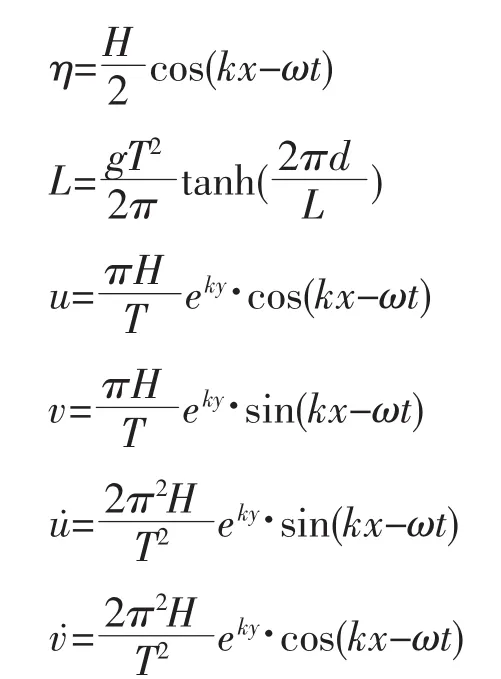
式中，T 为波周期（单位 s）；k为波数，k=2π/L；ω 为波频，ω=2π/T。

浮标浮体尺寸一般小于10 m，小于波浪波长，速度和加速度表达式中的y和x之间的关系可忽略。根据舟山外海和温州外海的浮标观测和数值模拟结果，大风期间海浪的周期T一般在7～9 s左右，计算可得波长L为77～126 m，波数k为0.05～0.08。当浮标吃水深度为D时，y=D，D一般在1 m左右，此时，eky→1。令 kx-ωt，则：

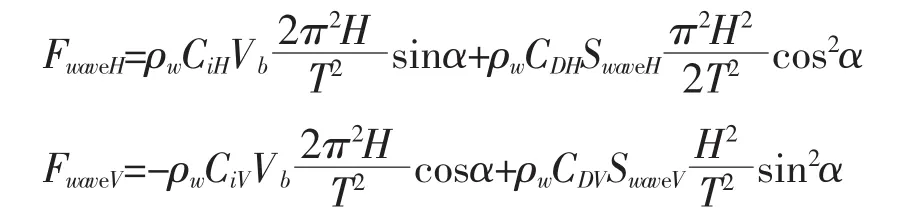
式中，CiH和CiV默认取1.0；CDH和CDV默认取0.5；π取3.14。将各参数代入上式，浪的作用力可简化为：

可见，当波高H和波周期T确定时，波浪作用力沿波浪质点的位置α变化。刘愉强等[6]认为，当α为0°或180°时，浪的作用力最大，但实际上，最大波浪作用力可以出现在圆周的任一点上，最易走锚的情形发生在波浪作用力沿锚链方向的分力最大时，即

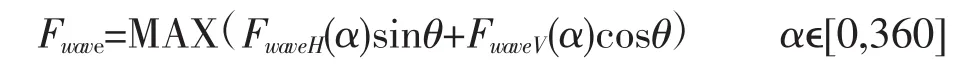
式中，θ为拉力与垂直方向的夹角。不考虑锚链的重力和悬垂，在极限情况下，锚链拉直，θ取决于锚链长度和水深。

1.1.4 风、流、浪的合力

在受力平衡条件下，浮体对锚的拉力取决于风、流、浪对浮标作用力沿锚链方向的分力，即

1.2 浮标锚系受力分析

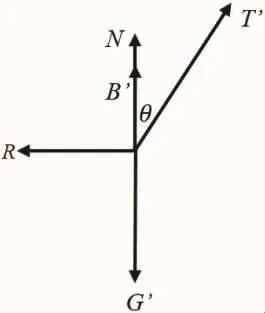
图2 锚的受力分析Fig.2 Force analysis of a anchor system

锚靠自身的重力以及与海底的摩擦力来阻止走锚现象，锚的受力（图2）可以写为：

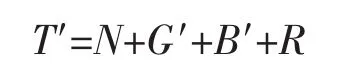
式中，T′为浮体对锚的拉力，T′=T；G′为锚的重力；B′为锚的浮力；N 为海底对锚的支撑力；R为锚的摩擦力。

锚的受力也可以分解为水平方向和垂直方向，在受力平衡条件下，

在水平方向上，拉力的水平分量与锚摩擦力平衡，即

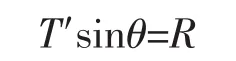
在垂直方向上，拉力的垂直分量与锚的重力、浮力和受到海底的支撑力平衡，即

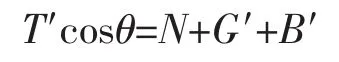
1.3 浮标泊稳条件

若要求不发生走锚，则要求浮标在风、浪、流作用下产生的拉力的水平分量应小于锚的最大摩擦力Rmax，即 Tsinθ≤Rmax

式中，Rmax=τN，τ为锚抓力系数，N=T′cosθ-G′-B′。

当风、流、浪等环境条件确定时，即可对特定浮标系统的泊稳条件进行计算，获得浮标系统所能承受的最大风速（风级），或者特定风级下浮标系统泊稳所需的最小锚重。

2 程序设计

2.1 界面和功能

近岸海洋浮标抗风等级计算软件基于Python 2.7语言编写，其界面如图3所示。程序计算需要输入两部分内容，一是环境变量，包括风速、流速及波浪信息等；二是浮体和锚系信息，如浮体直径、锚重、锚链长度等。

软件可以进行两种计算。一种是根据输入的信息和锚重，计算在当前条件下浮标系统所能承受的最大风级；另一种是根据输入的目标风级，计算在当前风级下，保证浮标系统不走锚所需要的最低锚重。

图3 程序输入输出界面Fig.3 GUI of input/output

2.2 环境变量设置

环境变量主要指的是风速（等级）、流速、海浪的波高和周期等。

为方便起见，风速以风级表示，8～16级风级和风速的对应关系见表1。

表1 风级和风速的对应关系Tab.1 The relationship between wind scales and wind speeds

大风条件下，近海海流主要由海表的潮流和风海流两部分组成。潮流呈周期性变化，安全起见取当地的最大潮流。风海流一般需要通过海流数值模型（如FVCOM、ROMS等模型）计算得到，但过程繁琐，花费时间较长。简便起见，程序中的风海流通过风速和经验系数计算得到。

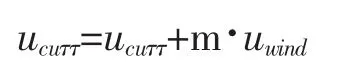
式中，uwind为最大潮流流速；m为经验系数，程序中取0.024。

程序中用于浮体受力计算的波浪变量为有效波高和波周期，可通过海浪数值模型（如SWAN等模型）计算得到，或依照观测和经验取值。

2.3 浮体及锚系信息

浮体信息包括浮体直径、高度和吃水深度等，用于计算受力分析所需的风受力面积、流受力面积、浮体湿水体积等。

锚系信息主要指锚的重量、锚链长度和锚抓力系数。锚抓力系数取决于锚的类型和底质类型。同样的锚在不同的底质上，锚抓力是不同的，在泥质底的锚抓力大于砂质底。浮标系统一般配备大抓力锚，如丹福尔锚、AC-14型锚，在泥质底的锚抓力系数为一般取10，在砂质底的锚抓力系数一般取8。

3 计算实例

3.1 抗风等级计算

以一个实际的海洋浮标为例（如图4所示），对浮标的抗风等级进行计算。标体表面直径 3.0 m，标体底面直径 1.5 m，型深 1.2 m，吃水深度0.8 m。浮标布放于浙江省舟山群岛嵊泗海域，布放水深约40 m，锚为丹福尔大抓力锚，锚重1t，锚链总长约80 m。计算时，波周期根据观测取7.5 s，有效波高依照经验在8～16级风下取6～14 m，呈线性递增，锚抓力系数取10。将各项参数输入软件后，点击“计算抗风等级”按钮，计算得到浮标抗风等级为8级。

图4 直径3 m的浮标Fig.4 A buoy with the diameter of 3 meter

该浮标于2018年10月5日“康妮”台风（编号1825）过境期间发生走锚。由当时的台风路径和风圈半径可以估算，台风过境时浮标海域风力达到8～9级，高于计算得到的浮标抗风等级，因此浮标发生了走锚现象。

图5是风、浪、流作用在浮体上的作用力在锚链方向的分量。由图可见，各作用力随风级的增大而增大，且在各风级下，浪对浮体的作用力都显著强于风、流的作用力。依风级不同，浪作用力约为流作用力的7～10倍，为风作用力的36～106倍。因此，在大风天气下的浮标受力分析和计算时，不应忽略海浪的作用。

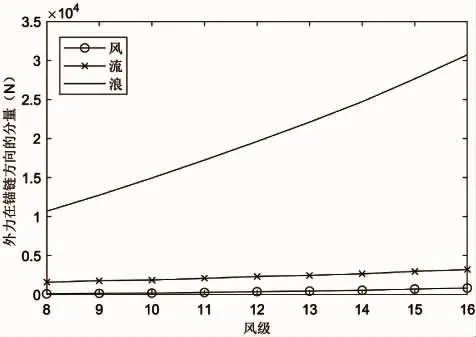
图5 风、浪、流作用在浮体上的作用力在锚链方向的分量Fig.5 The component along the anchor chain of the external force on the buoy of wind，current and wave

3.2 最低锚重计算

将各项参数输入软件后，设定目标风级，点击“锚重计算”按钮，可以得到保证上述浮标系统不走锚所需要的最低锚重。当前条件下，该浮标8～16级风不走锚所需最小锚重见表2。如果将锚链从80 m增长到120 m，即锚链长度由水深的2倍增加到水深的3倍，该浮标8～16级风不走锚所需最小锚重见表3。可见当锚链长度增加后，抵抗同等级风所需配备的锚重显著减小。

通过计算可以得知，该浮标配备的锚重较小、锚链长度较短，因此抵御大风的能力较低，可依照抗风等级计算结果适当增加锚重或锚链长度，或在大风期间对浮标进行回收以维护浮标系统安全。

表2 锚链长度为水深2倍时，浮标抗8～16级风所需最小锚重Tab.2 The minimum weight of anchor to anti-wind of 8 to 16 Beaufort scale when the length of the chain is 2 times of the water depth

表3 锚链长度为水深3倍时，浮标抗8～16级风所需最小锚重Tab.3 The minimum weight of anchor to anti-wind of 8 to 16 Beaufort scale when the length of the chain is 3 times of the water depth

4 结论

本文基于风、浪、流等环境变量对浮标系统的浮体和锚系分别进行了受力分析。其中，风和流的作用力以风压和流压的形式表示，而浪的作用力则同时考虑了波浪对浮体的压力以及浮体在波浪作用下的加速度。以标体对锚的拉力的水平分量不大于锚的最大锚抓力作为浮标的泊稳条件，本文采用Python 2.7编程语言编写了一套浮标抗风等级计算程序，用于计算特定浮标系统所能抵御的最大风级，以及特定风级下浮标系统泊稳所需的最小锚重。该程序被应用于嵊泗海域3 m浮标“康妮”台风（编号1825）期间走锚事件的分析。计算结果显示，该浮标在布放海域的最大抗风等级为8级，而“康妮”台风期间该海域风速为8～9级，因此发生了走锚现象。本研究可为浮标系统锚链长度和锚重配置计算、大风期间的浮标回收决策提供参考依据。

本文分析研究得出两个结论：（1）与前人认为当浮体位于波峰或波谷时浪的作用力最大的观点不同，本文计算了浪在整个波浪圆周上作用力，并取其沿锚链方向的分量的最大值作为浮标受力计算的条件。（2）进一步的分析表明，在不同风级下，海浪的作用力都显著强于风和流的作用力，为流作用力的7～10倍，为风作用力的36～106倍。因此，在大风天气下的浮标受力分析和计算时，不应忽略海浪的作用。