再入返回器极端热载荷预测方法

张思宇 余莉 曹旭 张章



再入返回器极端热载荷预测方法

张思宇1,2余莉1,2曹旭3张章3

（1 南京航空航天大学航空宇航学院，南京 210016） （2 南京航空航天大学飞行器环境控制与生命保障工信部重点实验室，南京 210016） （3 北京空间机电研究所，北京 100094）

为快速预测返回过程再入器的极端气动热载荷情况，文章以充气式再入器为研究对象，基于动力学运动方程及Kemp-riddell气动热工程公式，采用龙格-库塔方法开展了136组工况的返回过程数值计算，获得了充气式再入系统返回过程的轨迹弹道与驻点热流密度变化情况，研究了驻点热流密度峰值和峰值出现高度与弹道系数、球头半径及再入角度的关系，发现驻点热流密度随弹道系数、再入角度的增加而增加、与球头半径的二次方成反比；但极端热载荷出现高度随弹道系数增加而降低，与球头半径和再入角度无关。文章提出了航天器以第一宇宙速度返回再入时极端热载荷的工程经验公式，采用公式对飞船返回舱、返回式卫星的极端热载荷进行预测，所得结果和试验数据基本一致，表明该预测公式具有较高的准确性和较好的通用性。文章的预测方法适用于再入返回器的设计初期阶段，可快速预测返回器再入过程的极端气动热载荷，满足气动热估算需求，为再入器气动热防护方案的选择提供支持与参考。

气动减速 热载荷预测 气动热 热流密度 再入返回器

0 引言

再入是返回型航天器整个飞行任务的最后阶段，是整个飞行任务成败的最终标志，是航天员和空间应用科学实验结果安全返回地球的必经过程[1-2]。这一过程是航天器返回过程中飞行环境最恶劣、最复杂、最具危险性的一段，再入返回器以极高的速度在大气层中运动，周围空气受到强烈压缩并产生剧烈的摩擦，大部分动能将转化为热能，空气温度急剧升高，并向再入器表面传递热量，产生强烈的气动加热问题，使再入器表面温度急剧升高甚至产生烧蚀，从而可能导致结构破坏，是再入返回器热载荷设计重点关注的一段[3-7]。

目前对于高超声速流的气动热计算，主要有工程方法[8-10]、工程数值结合方法[11-12]及完全数值方法三种类型[13-16]。其中，工程算法通常基于经验公式求解热流密度，如Fay-Riddell公式、Kemp-riddell公式、Lees公式、Romig公式、Scala公式等，该方法计算效率高，对于简单外形，精确度也有一定保证，往往应用于再入器研制初期；工程数值结合方法是边界层外无粘数值求解和边界层内工程公式求解相结合的混合算法，该方法相对于数值方法提高了计算效率，相对于工程算法有更广的应用范围，常常用于复杂外形的高超声速飞行器设计计算；数值方法是通过直接求解N-S方程及其近似形式，如GASP程序、LAURA程序、GIANTS程序等，该方法计算精度对网格品质依赖大，此外计算量大，无法满足设计初期对再入全过程的气动热计算要求，常用于设计后期的验证对比。上述方法在计算前均需要预先进行弹道计算，无法快速得出热流密度峰值。

再入过程中航天器的驻点热流密度达到峰值时外层温度最高，因此在设计阶段，快速并且较为准确地预测驻点热流密度，可以为再入器设计阶段的气动热方案选择提供技术支持，并以此修正总体设计方案。本文以再入过程运动方程及热流密度工程公式为基础，通过对充气式减速锥不同弹道系数、不同气动外形、不同再入角度等共136种工况的计算，获得了热流密度峰值随弹道系数、球头半径、再入角度的变化规律，并拟合成了工程经验公式，上述拟合公式通过对“神舟”飞船返回舱、返回式卫星的计算并与真实飞行试验数据对比，误差在可接受范围内，表明该公式对于弹道式、半弹道式再入返回器具有一定的准确性和通用性，对快速预测返回器再入过程的极端气动热载荷及开展返回器热防护设计具有一定的指导意义。

1 计算模型

1.1 运动模型

1）不考虑侧向力作用，再入器在二维平面飞行；2）不考虑地球自转影响；3）飞行速度很大，气象风场影响可以忽略；4）下降过程气动外形不变。

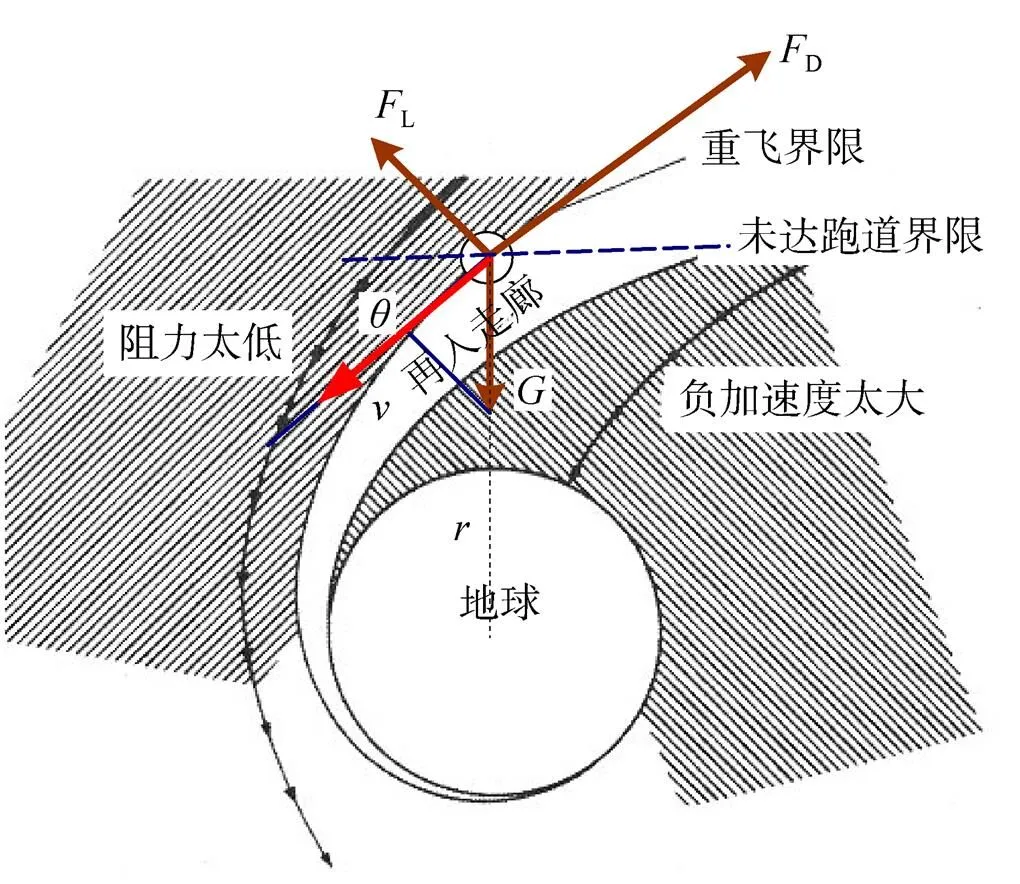
图1 再入过程受力情况

由此，建立如下运动方程：

此外，对于气动阻力与升力的计算，本文采用CFD仿真和牛顿压力公式的修正式结合的方法计算了整个再入过程的阻力系数与升力系数，并由此得到气动阻力与升力。

1.2 气动热模型

本文驻点气动热计算采用Kemp-Riddell公式：

再入过程中，壁面由非稳态向稳态过渡时间非常短，可以忽略，建立热平衡方程，则有：

1.3 模型验证

本文采用四阶Runge-kutta算法在MATLAB环境中开展编程计算。为验证本文模型的合理性和所编程序的准确性，采用文献[17]的数据进行验证计算，充气式再入器的发射质量308kg，迎风面最大直径3m，半锥角为60°，再入速度7 800m/s，再入高度150km，再入角为–3°，球头半径为0.38m。再入器为旋成体，质心配置在中心轴线上，为离地高度，为过载。

图2为采用本文模型的计算结果和文献结果[17]的对比情况。

图2 本文计算结果与文献[17]结果比较

从图2中可以看出：在减速性能、过载曲线、驻点热流曲线和驻点处壁面温度曲线四个方面，本文的计算结果均和文献结果趋势一致。其中着陆速度、过载、热流密度与壁温的误差对比结果如表1所示。

表1为本文计算结果与文献[17]结果对比，从表1中看出：除热流密度峰值误差略大外，其它参数的误差均在5%之内。再入返回器的驻点热流密度计算在自由分子流区、过渡流区和连续流区对应着不同的分析方法，但在自由分子流区和过渡流区时气动加热效应不明显且相对于热流密度峰值较小，热流密度峰值总是出现在连续流区。此外，由于不同的热流密度计算模型均存在一定的误差，本文采用的经典Kemp-riddell热流密度公式（偏差一般在5%左右）和文献[17]采取的Lees公式并不一致，考虑到高超声速气动热问题物理机制的复杂性，认为本文采用的热模型对于驻点热流密度峰值的计算是合理的。综上认为，本文建立的运动方程及计算方法是合理有效的。

表1 本文计算结果与文献结果对比

Tab.1 The calculation results compared with the literature results

2 热流密度预测

2.1 研究工况

本文以充气式再入器为研究对象，半锥角为60°，迎风面最大直径3m。采用正交设计方法开展了10组不同弹道系数、10组不同球头半径和3种不同再入角度，共136组研究工况的再入过程仿真计算。工况参数分别为：

2.2 结果分析

图3为不同工况下热流密度随海拔高度的变化情况。

从图3中看出：1）随弹道系数增加，再入返回器的驻点热流密度峰值增大，极端热载荷出现高度不断降低。这是由于弹道系数增加导致系统速度衰减变慢，极端热载荷出现的高度更低，空气密度更大，热流密度峰值增加。2）由于驻点热流密度和球头半径的平方根成反比，因而驻点热流密度峰值随球头半径的增大而减小，但峰值出现高度相同，如图3（b）所示。3）随再入角度增大，再入返回器的驻点热流密度峰值增大，极端热载荷出现高度不变。

再入返回器驻点处于热流密度峰值时，再入返回器整体处于最大热流状态，表面各处温度最高，最容易发生烧蚀。由式（2）可知，驻点热流密度和球头半径的平方根成反比，且受来流大气的影响。理想情况下，驻点热流密度峰值还与再入角度和弹道系数有关。

综合以上分析，驻点热流密度峰值满足如下关系式：

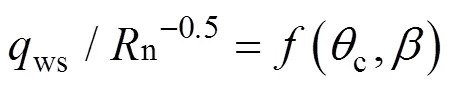
图3 热流密度随高度的变化

图4 驻点热流密度峰值随β变化

图5 驻点热流密度峰值随变化

为验证式（5）的准确性和通用性，本文对“神舟”飞船返回舱与返回式卫星的飞行工况进行验证，计算结果与飞行试验数据[18]进行对比验证，如表2所示。从中可以发现，对返回式卫星的最大相对误差为6.45%，对“神舟”飞船相对误差仅为2.31%，均具有较高的准确性。从计算结果中可以看出，本文提出的极端热载荷预测公式有较高的准确度。

表2 拟合值与飞行试验数据对比结果

Tab.2 Comparison of fitted values with flight test data

3 结论

本文以充气式再入器为对象，基于动力学运动方程及Kemp-riddell气动热工程公式，进行了136种工况再入过程的数值计算，通过对数据结果的分析，得出以下结论：

1）再入返回器的驻点热流密度随弹道系数、再入角度的增加而增加、与球头半径的二次方成反比；但极端热载荷出现高度随弹道系数增加而降低，与球头半径和再入角度无关。通过对热流密度及再入轨迹的分析，发现气动热峰值与弹道系数、球头半径、再入角度之间呈现幂函数关系，并由此提出了航天器以第一宇宙速度再入过程中最大热载荷的工程计算公式。

2）使用本文提出的工程计算公式对“神舟”飞船返回舱和返回式卫星进行计算，计算结果与试验数据基本一致，表明本文拟合的预测公式有较高的准确度和较好的通用性，能够满足再入返回器设计方案阶段的气动热估算需求。

3）本文的预测方法可快速预测返回器再入过程的极端气动热载荷，为再入器气动热防护方案的选择提供技术支持与指导，并以此修正返回器的总体设计方案。

[1] 许家裕. 充气式返回飞行器的结构动态特性分析[D]. 哈尔滨: 哈尔滨工业大学, 2012. XU Jiayu. Structural Dynamic Characteristics Analysis of Inflatable Re-entry Vehicle[D]. Harbin: Harbin Institute of Technology, 2012. (in Chinese)

[2] WANG Rui, HOU Anping, NIU Yonghong. The Optimal Design & Analysis of the IRDT System Based on Two-dimensional Ballistic Trajectory in Atmosphere Reentry[C]//20th AIAA International Space Planes & Hypersonic Systems & Technologies Conference. Glasgow, Scotland: AIAA, 2015.

[3] 卫剑征, 谭惠丰, 王伟志, 等. 充气式再入减速器研究最新进展[J]. 宇航学报, 2013(7): 881-890. WEI Jianzheng, TAN Huifeng, WANG Weizhi, et al. New Trends in Inflatable Re-entry Aeroshell[J]. Journal of Astronautics, 2013(7): 881-890. (in Chinese)

[4] CORSO J A, CHEATWOOD F M. Advanced High-temperature Flexible TPS for Inflatable Aerodynamic Decelerators[C]//21st AIAA Aerodynamic Decelerator Systems Technology Conference & Seminar. Dublin, Ireland: AIAA, 2011.

[5] 陈红永, 陈海波. 近空间飞行器再入段载荷特性分析[J]. 飞行力学, 2013(5): 443-446. CHEN Hongyong, CHEN Haibo. Load Analysis of Near-space Vehicle in Reentry Stage[J]. Flight Dynamics, 2013(5): 443-446. (in Chinese)

[6] HUGHES S J, DILLMAN R A. Inflatable Re-entry Vehicle Experiment (IRVE) Design Overview[C]//18th AIAA Aerodynamic Decelerator Systems Technology Conference &Seminar. Munich, Germany: AIAA, 2005.

[7] HUGHES S J, CHEATWOOD D F. Hypersonic Inflatable Aerodynamic Decelerator (HIAD) Technology Development Overview[C]//21st AIAA Aerodynamic Decelerator Systems Technology Conference & Seminar. Dublin, Ireland: AIAA, 2011.

[8] 李建林, 唐乾刚, 霍霖, 等. 复杂外形高超声速飞行器气动热快速工程估算[J]. 国防科技大学学报, 2012(6): 89-93. LI Jianlin, TANG Qiangang, HUO Lin, et al. The Rapid Engineering Aero-heating Calculation Method for Complex Shaped Hypersonic Vehicles[J]. Journal of National University of Defense Technology, 2012(6): 89-93. (in Chinese)

[9] 骆广琦, 胡砷纛, 李游, 等. 高超声速飞行器变比热驻点热流计算[J]. 科技导报, 2015(22): 55-59. LUO Guangqi, HU Shendao, LI You, et al. The Calculation of the Heat Flux at the Stagnation Point in Consideration of Variable Specific Heat for Hypersonic Vehicle[J]. Science & Technology Review, 2015(22): 55-59. (in Chinese)

[10] 吕丽丽, 张伟伟, 叶正寅. 高超声速再入体表面热流计算[J]. 应用力学学报, 2006(2): 259-262. LYU Lili, ZHANG Weiwei, YE Zhengyin. Predicting Heating Distributions for Hypersonic Reentry Bodies[J]. Chinese Journal of Applied Mechanics, 2006(2): 259-262. (in Chinese)

[11] 贾志强. 飞行器气动加热数值与工程结合计算方法研究[D]. 上海: 上海交通大学, 2012. JIA Zhiqiang. The Calculation Method of Aerodynamic Heating with United Numerical and Engineering Algorithm[D]. Shanghai: Shanghai Jiao Tong University, 2012. (in Chinese)

[12] 王杰. 高超声速飞行器气动加热计算技术[D]. 南京: 南京航空航天大学, 2012. WANG Jie. Calculating Method of Aerodynamic Heating for Hypersonic Aircrafts[D]. Nanjing: Nanjing University of Aeronautics & Astronautics, 2012. (in Chinese)

[13] 吴洁, 阎超. 气动热与热响应的耦合研究[J]. 导弹与航天运载技术, 2009(4): 35-39. WU Jie, YAN Chao. Research on the Coupling of Aerodynamic Heating & Thermal Response[J]. Missiles & Space Vehicles, 2009(4): 35-39. (in Chinese)

[14] 蒋友娣. 高超声速飞行器气动热和表面瞬态温度计算研究[D]. 上海: 上海交通大学, 2008. JIANG Youdi. Calculation of Aerodynamic Heating & Transient Surface Temperature for Hypersonic Aircraft[D]. Shanghai: Shanghai Jiao Tong University, 2008. (in Chinese)

[15] AI Bangcheng, MAO Guoliang. Coupled Aeroheating Structure Analysis with CFD Methods[C]//54th International Astronautical Congress of the International Astronautical Federation. Bremen, Germany: the International Academy of Astronautics & the International Institute of Space Law, 2003.

[16] MCDANIEL R, WRIGHT M J. Aeroheating Predictions for Phoenix Entry Vehicle[C]//46thAIAA Aerospace Sciences Meeting &Exhibit. Reno, Nevada: AIAA, 2008.

[17] 高艺航, 贺卫亮. 充气式返回舱气动热特性研究[J]. 航天返回与遥感, 2014, 35(4): 17-25. GAO Yihang, HE Weiliang. Research on Aerodynamic Heating Characteristics of Inflatable Reentry Decelerator[J]. Spacecraft Recovery & Remote Sensing, 2014, 35(4): 17-25. (in Chinese)

[18] 叶培建, 杨孟飞, 彭兢, 等. 中国深空探测进入/再入返回技术的发展现状和展望[J]. 中国科学: 技术科学, 2015(3): 229-238. YE Peijian, YANG Mengfei, PENG Jing, et al. Review & Prospect of Atmospheric Entry &Earth Reentry Technology of China Deep Space Exploration[J]. Scientia Sinica Technologica, 2015(3): 229-238. (in Chinese)

Prediction Method for Extreme Thermal Load of Reentry Capsule

ZHANG Siyu1,2YU Li1,2CAO Xu3ZHANG Zhang3

（1 College of Aerospace Engineering, Nanjing University of Aeronautics & Astronautics, Nanjing 210016, China）（2 Key Laboratory of Aircraft Environment Control and Life Support, MIIT, Nanjing 210016, China）（3 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）

In order to quickly predict the maximum thermal load of the reentry capsule during re-entry process, the numerical calculation of the return process of inflatable decelerator under 136 cases is carried out based on dynamic equations and Kemp-riddell aeroheating formula with Runge-kutta method. The trajectory and the heat flux density on stagnation point of the inflatable reentry system are obtained in the reentry process. The rules of thermal peak and its height with different ballistic coefficient, nose radius and reentry angle are studied. The results show that heat flux density on stagnation point increases with the ballistic coefficient, reentry angle, and is inversely proportional to the square of the nose radius. However, the height of the maximum thermal load decreases with the ballistic coefficient, which is irrelevant to the nose radius and the reentry angle. Based on analysis, an empirical formula for extreme heat load of reentry capsule at the first cosmic velocity is fitted in the reentry process. The formula is used to predict the extreme thermal load of reentry capsule and returnable satellite, and the results are consistent well with the experimental data. It shows that the empirical formula has higher accuracy and better versatility. The method in this paper is applied to the early stage of reentry capsule design, which can rapidly predict the extreme thermal load in the reentry process and meet the estimation demand of aeroheating. It provides support and guidance for the selection of thermal protection schemes of reentry capsule.

aerodynamic deceleration; thermal load prediction; aeroheating; heat flux density; reentry capsule

V475.9

A

1009-8518(2019)02-0025-08

10.3969/j.issn.1009-8518.2019.02.003

张思宇，男，1995年生，2018年获南京航空航天大学飞行器环境与生命保障工程专业工学学士学位，现在南京航空航天大学航空学院人机与环境工程专业攻读工学博士学位。研究方向为流固耦合力学、飞行器安全救生及生命保障。E-mail：zhangsiyu@nuaa.edu.cn。

2018-09-18

国家自然科学基金（11602018）；江苏高校优势学科建设工程

（编辑：刘颖）