ULE®叠层反射镜二维等效建模方法研究
丁锴铖 连华东
ULE®叠层反射镜二维等效建模方法研究
丁锴铖1,2连华东1
(1 北京空间机电研究所,北京 100094) (2 先进光学遥感技术北京市重点实验室,北京 100094)
ULE®叠层反射镜是实现大口径、低面密度、高刚度空间反射镜的有效途径。为提高ULE®叠层反射镜设计效率,文章基于蜂窝夹芯结构均质板等效理论,推导了叠层反射镜二维等效模型建模方法,利用有限元法计算二维等效模型自由模态频率,对比详细模型计算结果,验证等效模型计算精度,并结合设计实例验证该二维等效模型在叠层反射镜优化设计中的有效性。分析结果表明,叠层反射镜面密度大于40kg/m2时,二维等效模型模态频率计算误差优于4%,满足优化设计精度要求。文章提出的叠层反射镜二维等效建模方法大幅缩减叠层反射镜有限元模型规模,实现叠层反射镜有限元模型高度参数化,有效提高了叠层反射镜设计效率。
叠层反射镜 等效理论 轻量化 有限元分析 航天遥感
0 引言
ULE®叠层反射镜是为实现大口径、低面密度、高刚度空间反射镜而提出的新型蜂窝夹芯构型,蜂窝芯采用多层不同形状、不同尺寸的组合蜂窝结构[1-3]。地球之眼系列(Geo-Eye)1.1m口径空间主镜采用叠层技术实现了50kg/m2面密度[4],为制备4~8m口径的空间反射镜,文献[5]已研制出面密度为45kg/m2,口径分别为430mm与 1 500mm口径鉴定产品,我国也已实现500mm口径与3m口径鉴定产品的研制,可以预见其在大口径空间反射镜轻量化设计中的应用前景[6]。随着叠层反射镜应用需求增加,对其设计效率提出了更高要求。
为提高反射镜设计效率,通常先确定一个面形精度、基频、质量等指标接近或满足设计指标的初始镜体结构。传统方法利用设计经验或经验公式确定反射镜径厚比,蜂窝胞元形状、大小,面板厚度等结构参数[7-8],而叠层反射镜结构形式新颖,缺乏设计参考,采用经验公式误差较大,设计结果不可靠;文献[9]、[10]提出一种基于二维等效模型的反射镜结构优化方法,将具有蜂窝孔的轻量化反射镜等效成一层均质薄板,在有限元软件中用一层2D壳单元表征镜体结构,简化模型,缩短建模及计算耗时,从而提高设计效率:然而文献[9]中总结的二维等效模型仅考虑了单一蜂窝构型,不能直接应用于由多层不同尺寸、形状的蜂窝芯组合成型的叠层反射镜。因此,在叠层反射镜优化设计过程中,目前要通过描述全部筋板、面板等结构的详细有限元模型进行分析。这类模型建模复杂、修改困难、规模庞大、计算费时,导致ULE®叠层反射镜的设计效率较低。
针对上述问题,本文基于蜂窝夹芯结构均质板等效理论推导了ULE®叠层反射镜二维等效建模方法,通过数值仿真验证了二维等效模型的计算精度,基于二维等效模型建立了叠层反射镜优化设计流程,并结合设计实例验证了二维等效建模方法在ULE®叠层反射镜优化设计中的实用性与高效性。
1 叠层反射镜二维等效模型公式推导
叠层反射镜结构如图1所示,定义反射镜光学表面中心为坐标原点;f、b为前、后面板厚度;c为蜂窝芯壁厚;A为光学平面至中性面之间的距离;h、B分别为第层蜂窝的芯层高度以及蜂窝孔筋板间距,下标代表第层蜂窝芯对应属性,一般≤3;为反射镜总高度。

图1 叠层反射镜示意图
文献[10]中单一蜂窝胞元结构等效建模方法,定义第层蜂窝芯密实度比α为

中性面A计算方法如下

式中()为距光学表面处蜂窝芯的密实度比。
二维等效模型是将叠层反射镜等效为一层均质薄板,在有限元中用1层板壳单元计算,提高反射镜建模与计算效率[11]。二维等效均质薄板的等效厚度eq,等效密实度比,单位宽度上的弯曲惯性矩b和剪切深度计算方法如下

根据面内刚度等效、面外刚度等效、质量等效原理[12-15],推导得二维等效均质薄板的材料参数计算方法

式中k为第层蜂窝芯蜂窝形状修正系数[16],正六边形蜂窝k=2,正三角形蜂窝k=3;、、、为反射镜材料的泊松比、弹性模量、剪切模量和密度;eq、eq、eq、eq分别代表等效板的泊松比、弹性模量、剪切模量和密度。
2 二维等效模型精度分析
2.1 反射镜有限元建模
本文利用Hypermesh进行建模、分析。针对三层蜂窝的平面叠层反射镜,建立二维等效模型计算1阶自由模态频率,以详细模型计算结果作为精确值,分析二维等效模型精度[17]。保持其它参数不变,分别改变反射镜总高度和层高比f︰1︰2︰3︰b,研究不同径厚比、面密度对二维等效模型计算精度的影响。反射镜的不变参数如表1所示。图2为=60mm,f︰1︰2︰3︰b=1︰2︰4︰2︰1时两种建模方法的有限元模型。
表1 反射镜主要几何参数

Tab.1 Main geometric parameters of the stacked-core mirror mm
如图2所示,详细模型中面板、蜂窝壁、内外环均采用板单元,总单元数为112 812个;二维等效模型在反射镜中面位置建立板单元,反射镜内、外环以梁单元表示,单元数为3 840个,其中板单元3 600个,梁单元240个。可以看出,二维等效模型在建模复杂程度上远低于详细模型,对于结构复杂的叠层反射镜,建模时间可从数小时缩短至几分钟,建模与分析时间大幅降低。

图2 叠层反射镜有限元模型
2.2 二维等效模型精度验证
保持层高比f︰1︰2︰3︰b=1︰2︰4︰2︰1不变,反射镜总高度以10mm为步长从30mm增加至110mm,计算反射镜模态频率。结果如表2所示。
表2 径厚比对二维等效模型精度影响

Tab.2 Influence of diameter-thickness ratio on natural frequency error
保持反射镜高度=80mm不变,改变层高比,研究不同面密度对二维等效模型频率计算精度的影响,结果如表3所示。不同参数对二维等效模型计算精度的影响如图3所示。
表3 轻量化程度对二维等效模型精度影响
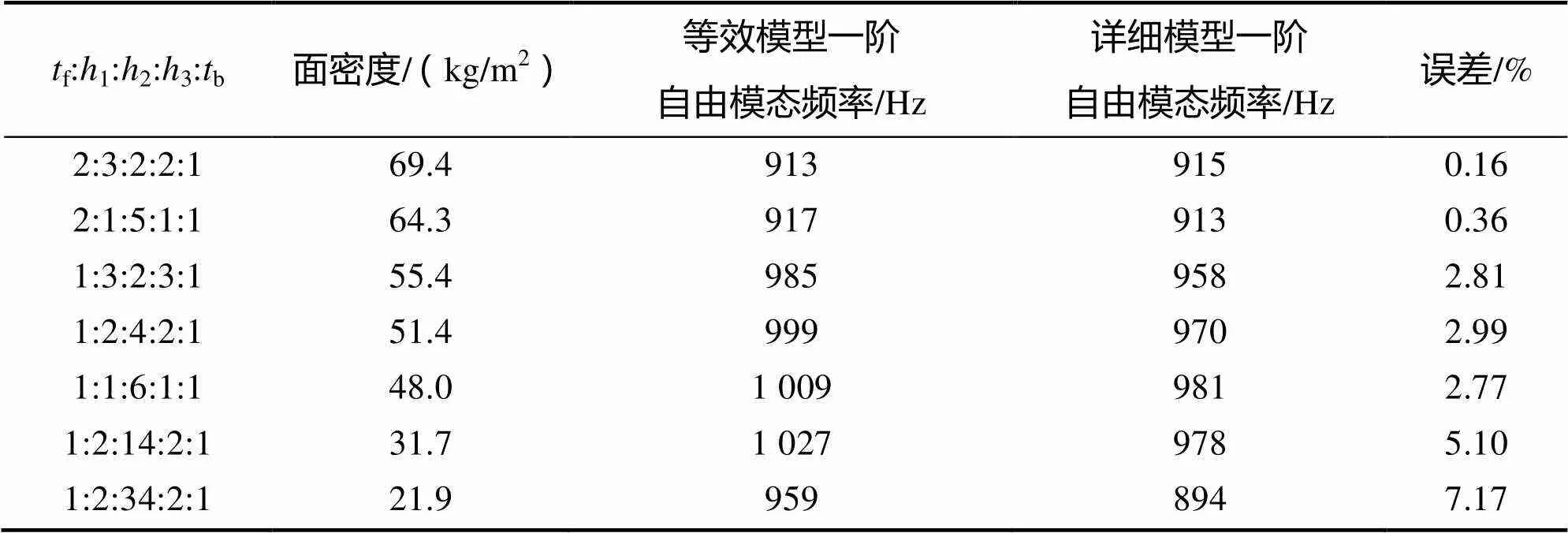
Tab.3 Influence of lightweight degree on natural frequency error
综合表2、表3及图3可以看出:二维等效模型分析结果普遍偏高,叠层结构在等效过程中刚度得到加强;二维等效模型计算结果在变化趋势上与详细模型计算结果高度一致;径厚比变化对叠层反射镜二维等效模型精度影响有限,面密度对二维等效模型频率计算精度影响更明显,当叠层反射镜面密度大于40kg/m2时,二维等效模型频率计算误差小于4%。综上所述,叠层反射镜二维等效模型计算精度满足优化设计要求,相较于详细模型,二维等效模型在简化模型、缩短计算耗时方面有巨大优势,可有效提高叠层反射镜设计效率。

图3 不同参数对二维等效模型频率误差的影响
2.3 算例分析
基于叠层反射镜二维等效模型对某大口径非球面反射镜进行轻量化设计,进一步验证二维等效模型在叠层反射镜优化设计中的实用性及有效性。反射镜设计要求如表4所示[12]。
表4 反射镜设计要求

Tab.4 Design requirements of the mirror
以质量最小为目标,光轴平行重力时背部36点卸载面形为约束优化反射镜。首先,根据反射镜形 状参数建立1层板壳有限元模型,结合工程经验确定各变量设计范围,利用中心复合设计法建立采样 点[18-20],计算等效参数并更新有限元模型进行分析,提取储存面形分析结果直至所有采样点计算完成,然后拟合完全二次多项式响应面模型,基于响应面模型进行优化[21-23],最后根据优化结果建立详细模型进行验证,直至满足设计要求。优化流程如图4所示,叠层反射镜各结构参数对反射镜面形的影响程度如图5所示。
按图4所示流程及图5灵敏度分析结果,建立响应面模型进行优化,结果如表5所示。
根据表5所示参数建立以板壳结构为主的详细模型进行校核,二维模型与详细模型计算结果如表6所示。
对比二维等效模型设计结果与详细模型仿真结果,面形计算误差为7.43%,频率计算误差为2.33%,质量计算误差为2.56%,满足设计要求;基于二维等效模型建立的叠层反射镜优化设计方法将有限元模型高度参数化,大幅提高了这类反射镜的设计效率。

图4 叠层反射镜优化流程

图5 叠层反射镜各结构参数对面形的影响
表5 反射镜结构参数优化结果

Tab.5 The optimized results of the mirror structur parameters mm
表6 等效模型与详细模型计算结果对比

Table.6 Comparison of results between 2D model and detailed model
3 结束语
基于蜂窝结构均质板等效理论,推导出ULE®叠层反射镜二维等效刚度模型各参数计算方法。研究不同径厚比、面密度下二维等效模型一阶自由模态频率计算精度,结果表明面密度大于40kg/m2时,二维等效模型频率计算误差优于4%,具有工程实用价值;通过具体算例验证了该二维等效模型在叠层反射镜优化设计中的有效性。后续将进一步研究变刚度分布的叠层反射镜等效建模方法,提高叠层反射镜二维等效模型适用范围;利用二维等效建模方法实现叠层反射镜设计过程自动化,提高叠层反射镜设计效率。
[1] 刘韬. 国外静止轨道大口径反射成像技术发展综述[J]. 航天返回与遥感, 2016, 37(5): 1-9. LIU Tao. An Overview of Development of Foreign Large Aperture Reflection Imaging Technology on Geostationary Orbit[J]. Spacecraft Recovery & Remote Sensing, 2016, 37(5): 1-9. (in Chinese)
[2] SABIA R, EDWARDS M J, VANBROCKLIN R, et al. Corning 7972 ULE Material for Segmented and Large Monolithic Mirror Blanks[C]//SPIE Astronomical Telescopes + Instrumentation. International Society for Optics and Photonics, 2006.
[3] STAHL H P. Advanced Mirror Technology Development for Very Large Space Telescopes[C]//American Astronomical Society Meeting. Baltimore, MD: American Astronomical Society Meeting Abstracts #223, 2011.
[4] EGERMAN R, MATTHEWS G, WYNN J, et al. The Current and Future State-of-the-art Glass Optics[C]//Astro2010: The Astronomy and Astrophysics Decadal Survey. 2009.
[5] STAHL H P. Advanced Mirror Technology Development (AMTD) Project: Overview and Year Four Accomplishments[C]//SPIE Astronomical Telescopes + Instrumentation. Edinburgh, United Kingdom, 2016.
[6] 刘红. 低面密度叠层蜂窝低膨胀玻璃质反射镜研制技术[C]//第三届空间光学与遥感应用论坛. 北京: 北京空间机电研究所, 2017. LIU Hong. Manufacturing Technology of Low Area Density Stacked-core Mirror Using Low Expansion Glass[C]//The Third Space Optics and Remote Sensing Applications Forum. Beijing: Beijing Institute of Space Mechanics & Electricity, 2017. (in Chinese)
[7] 宫辉, 连华东. 大口径双拱型SiC反射镜背部构型初步研究[J]. 航天返回与遥感, 2010, 31(4): 32-37. GONG Hui, LIAN Huadong. Preliminary Study on Backside Structure of Large-aperture Double-arch SiC Mirror[J]. Spacecraft Recovery & Remote Sensing, 2010, 31(4): 32-37. (in Chinese)
[8] VANDERPLAATS G N. Numerical Optimization Techniques for Engineering Design: With Application[J]. Computer Aided Optimal Design: Structural and Mechanical Systems, 2005, 27(4): 197-239.
[9] 凯斯·B·道尔, 维克托·L·基恩伯格, 格雷戈里·J·迈克尔斯. 光机集成分析[M]. 连华东, 王小勇, 徐鹏, 译. 北京: 国防工业出版社, 2015. DOYLE K B, GENBERG V L, MICHELS G J. Integrated Optomechanical Analysis[M]. LIAN Huadong, WANG Xiaoyong, XU Peng, translated. Beijing: National Defend Industry Press, 2015. (in Chinese)
[10] YODER P. Opto-mechanical Systems Design, Fourth Edition, Volume 2: Design and Analysis of Large Mirrors and Structures[M]. CRC Press, 2015.
[11] 蒋权, 杨洪波, 李宗轩, 等. 光学小卫星蜂窝主承力板的设计与测试[J]. 红外与激光工程, 2016, 45(12): 242-249. JIANG Quan, YANG Hongbo, LI Zongxuan, et al. Design and Experiment of Honeycomb Sandwich Plate of Optical Small Satellite[J]. Infrared and Laser Engineering, 2016, 45(12): 242-249. (in Chinese)
[12] 刘健, 周春燕. 长厚比对正六边形铝蜂窝夹层板等效板模型动力学计算精度的影响[J]. 复合材料学报, 2016, 33(8): 1838-1847. LIU Jian, ZHOU Chunyan. Influence of Length-thickness Ratio on Dynamics Calculation Accuracy of Equivalent Plate Model of Hexagonal Aluminum Honeycomb Sandwich Plate[J]. Acta Materiae Compositae Sinica, 2016, 33(8): 1838-1847. (in Chinese)
[13] 张铁亮, 丁运亮, 金海波. 蜂窝夹层板结构等效模型比较分析[J]. 应用力学学报, 2011, 28(3): 275-282. ZHANG Tieliang, DING Yunliang, JIN Haibo. Comparative Analysis of Equivelent Models for Honeycomb Sandwich Plates[J]. Chinese Journal of Applied Mechanics, 2011, 28(3): 275-282. (in Chinese)
[14] 谭陆洋, 王栋, 李林, 等. 光学小卫星主载荷承力结构的多工况优化设计[J]. 红外与激光工程, 2017, 46(12): 272-278. TAN Luyang, WANG Dong, LI Lin, et al. Multi-condition Optimization Design of Main Load Bearing Structure of Optical Small Satellite[J]. Infrared and Laser Engineering, 2017, 46(12): 272-278. (in Chinese)
[15] 富明慧, 徐欧腾, 陈誉. 蜂窝芯层等效参数研究综述[J]. 材料导报, 2015, 29(5): 127-134. FU Minghui, XU Outeng, CHEN Yu. An Overview of Equivalent Parameters of Honeycomb Cores[J]. Materials Review, 2015, 29(5): 127-134. (in Chinese)
[16] LUCA G, ALDO S. Dynamic Modeling of Honeycomb Sandwich Panel[J]. Archive of Applied Mechanics, 2007, 11(11): 779-793.
[17] CHENG Q H, LEE H P, LU C. A Numerical Analysis Approach for Evaluating Elastic Constants of Sandwich Structures with Various Cores[J]. Composite Structures, 2006, 74(2): 226-236.
[18] GENBERG V L, MICHELS G J. Using Integrated Models to Minimize Environmentally Induced Wavefront Error in Optomechanical Design and Analysis[C]//SPIE Optics Engineering + Applications. San Diego, California, 2017.
[19] 杨佳文, 黄巧林. 大口径反射镜结构参数优化设计[J]. 中国空间科学技术, 2011, 31(4): 77-83. YANG Jiawen, HUANG Qiaolin. Optimized Design of Structure Parameters for Large-aperture Mirrors[J]. Chinese Space Science and Technology, 2011, 31(4): 77-83. (in Chinese)
[20] XIAO G, ZHU Z. Friction Materials Development by Using DOE/RSM and Artificial Neural Network[J]. Tribology International, 2010, 43(1): 218-227.
[21] 郭勤涛, 张令弥, 费庆国. 用于确定性计算仿真的响应面法及其试验设计研究[J]. 航空学报, 2006, 27(1): 55-61. GUO Qintao, ZHANG Lingmi, FEI Qingguo. Response Surface Method and Its Experimental Design for Deterministic Computer Simulation[J]. Acta Aeronauticaet Astronautica Sinica, 2006, 27(1): 55-61. (in Chinese)
[22] 李宗轩, 邢利娜, 解鹏. 视频空间相机Φ330mm口径主镜组件设计[J]. 光子学报, 2016, 45(7): 12-17. LI Zongxuan, XING Lina, XIE Peng. Design of the Φ330 mm Primary Mirror Assembly of Spaceborne Video Camera[J]. Acta Photonica Sinica, 2016, 45(7): 12-17. (in Chinese)
[23] 包奇红, 沙巍, 陈长征, 等. 空间SiC反射镜背部中心支撑特性[J]. 光子学报, 2017, 46(2): 22-31. BAO Qihong, SHA Wei, CHEN Changzheng, et al. Characteristics of Rear Support in Centre for Space SiC Mirror[J]. Acta Photonica Sinica, 2017, 46(2): 21-31. (in Chinese)
2D Equivalent Modeling Method for ULE®Stacked-core Mirrors
DING Kaicheng1,2LIAN Huadong1
(1 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China) (2 Beijing Key Laboratory of Advanced Optical Remote Sensing Technology, Beijing 100094, China)
ULE®stacked-core mirror technology provides an effective way to make space mirrors with large aperture, low areal density and high stiffness.In order to improve the design efficiency and accuracy for ULE®stacked-core mirrors, a 2D equivalent modeling method is derived based on equivalent plate theory for sandwich structure in this paper. The finite element method is used to calculate the free modal frequency of the 2D equivalent model, and then the results are compared with those obtained by detailed model to verify the accuracy of the equivalent method. The validity of the 2D equivalent model in the optimization design of the stacked-core mirror is verified by a simulation example. The results show that the frequency error of 2D equivalent model is less than 4% when the areal density of the stacked-core mirror is greater than 40kg/m2, which can satisfy the requirements of the mirror design optimization.The 2D equivalent method proposed in the paper can greatly reduce the scale of the finite element model and increase the parameterization level highly, thus effectively improving the design efficiency for the stacked-core mirrors.
stacked-core mirrors; equivalent method; lightweight; finite element analysis; space remote sensing
TH75;V414.6
A
1009-8518(2019)02-0099-08
10.3969/j.issn.1009-8518.2019.02.011
丁锴铖,男,1991年生,2014年获哈尔滨工业大学航空宇航科学与技术专业学士学位,现在中国空间技术研究院飞行器设计专业攻读硕士学位。研究方向为光学遥感器总体设计。E-mail:mldingding@sina.com。
2018-06-07
国家重大科技专项工程
(编辑:庞冰)

