基于1-1-3型压电复合材料水声换能器性能分析

杜海波, 秦雷,2, 仲超, 王丽坤,2

1．北京信息科技大学传感器北京市重点实验室，北京100192;2．北京信息科技大学教育部现代测控技术重点实验室，北京100192

1-3型压电复合材料由于其制备工艺简单、压电性强、机电耦合系数大等优势,被广泛应用于超声无损检测、海底测绘成像等领域[1-3]。近年来,为进一步提高1-3型压电复合材料的性能,一方面,研究者试图通过改变复合材料中的主动性材料性能来提高复合材料性能。如Wang等人应用0.32PIN-0.35PMN-0.33PT(PIMNT)制备了1-3型压电复合材料,压电单晶PIMNT体积百分比为60%时,厚度机械耦合系数可以达到84%[4]。另一方面,部分研究者通过改变复合材料中的被动性材料来提高复合材料性能。如哈尔滨工业大学王、张等人研究发现压电复合材料中聚合物刚度越小,复合材料压电性能越好[5]。同时,该课题组研究了硅橡胶与环氧树脂作为聚合物时压电复合材料的压电性能。结果表明在常温至140℃时,采用硅橡胶作为聚合物的性能更加优异[6]。此外,还有一部分研究者通过改变复合材料的结构来提高复合材料的性能。如陕西师范大学应用声学研究所的鲜晓军等人通过设计制作类1-3-2型压电复合材料,并对类1-3-2型压电复合材料的基元进行布阵,所研制的类1-3-2型换能器具有高发射响应、宽频带等优点[7]。中国科学院声学研究所的靳登攀等人通过设计了一种高效的小型大功率无指向性的球形宽带发射换能器,其最大声源级达到200 dB以上,电声效率达到50%[8]。

本课题组在前期提出一种1-1-3型压电复合材料。即在1-3型复合材料陶瓷柱与环氧树脂之间灌注柔性聚合物硅橡胶形成压电复合材料,这样可以减小环氧树脂对陶瓷柱的束缚作用并且可以减小基元间的横向耦合,提高能量转换效率[9-11]。本文拟在上述研究基础上进一步研究1-1-3型压电复合材料在水声换能器中的应用。试图在1-1-3型压电复合材料声辐射端引入梯形结构匹配层,以增大发射面积的作用,从而提高换能器的发射电压响应和接收灵敏度以及带宽的目的。

1 复合材料结构

本文提出的添加梯形匹配层的1-1-3型压电复合材料结构如图1a)所示,它由压电陶瓷柱、环氧树脂骨架、硅橡胶填充物以及环氧树脂匹配层构成。其中压电陶瓷柱沿厚度Z方向极化,厚度为t1,是整个压电复合材料的主动振动元件。只在Z方向自我连通的柔性聚合物硅橡胶包围在陶瓷柱四周。三维自我连通的环氧树脂与柔性聚合物硅橡胶连接并作为支撑整个复合材料的骨架。环氧树脂匹配层粘接于压电陶瓷柱表面,厚度为t2,环氧树脂与压电陶瓷柱接触部分为梯形结构。在陶瓷柱与环氧树脂之间填充的柔性聚合物硅橡胶,降低了环氧树脂骨架对陶瓷柱的束缚,这样每个陶瓷柱接近于自由振动,减小了基元间横向耦合,提高了机电耦合系数。辐射端添加如图1b)所示的梯形匹配层,其中下表面为分割的小正方形,上表面为完整的方形,此结构能够将每个陶瓷柱的自由振动转变成整个匹配层上表面的振动,可以增大辐射面积,提高发射电压响应。减小匹配层下表面面积,可使接收的声压信号变大,提高换能器的接收灵敏度。

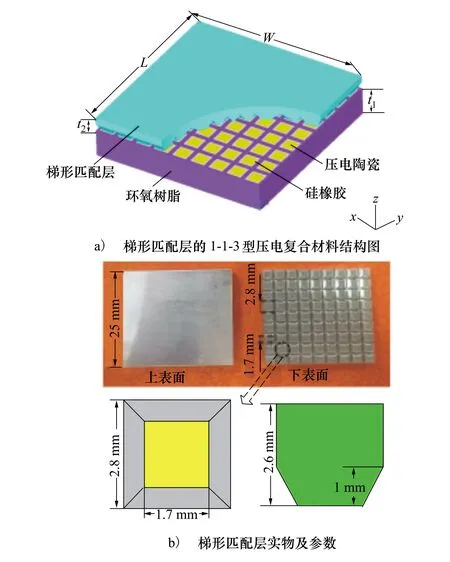
图1 复合材料结构参数

2 复合材料有限元仿真

本文使用有限元分析软件Ansys(ANSYS.Inc,USA)分析压电复合材料的电学性能和振动特性。如图2所示,由于1-1-3型压电复合材料具有周期对称性,单个基元的电学与振动特性就可表征整个复合材料的特性。因此,出于提高运算速度的考虑,本文选取单个基元进行建模、仿真。分别建立了无匹配层与添加梯形匹配层的基元模型如图3所示。图3a)表示1-1-3型压电复合材料单个基元的有限元模型,图3b)表示带有梯形匹配层的有限元模型,本文选择1/4波长作为匹配层的厚度。建立复合材料实体模型后,按照表1～3给出的参数,定义单元类型、设置材料参数。根据1/10波长的原则进行网格划分。然后根据图2给出的对称性,在单个基元模型四边加载对称边界条件,在模型Z方向的顶部与底部上施加1 V和0 V的电压,然后进行求解。在谐响应分析中,选择频率范围为220～450 kHz,分成230个子步,每一步间隔1 kHz。在后处理中,得到上表面的电量Q,再通过积分计算出电流I,根据公式I/V计算得到基元的电导曲线,计算结果如图4所示。由图可见,2种基元分别在352 kHz和363 kHz处产生谐振,且谐振峰较为单纯,无其他模态干扰。所制备材料尺寸如表2所示。

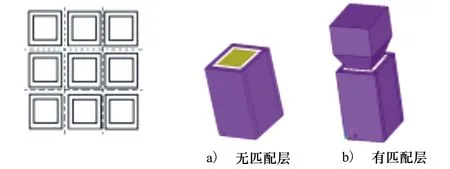
图2 1-1-3型压电复合 图3 1-1-3型复合材料 材料对称结构 基元振子

PZT-5A参数值ρ/(kg·m-3)7 750εs33/ε0830cE11/(1010N·m-2)12.1cE12/(1010N·m-2)7.54cE13/(1010N·m-2)7.52cE33/(1010N·m-2)11.1cD13/(1010N·m-2)14.7h33/(108V·m-1)21.5e31/(C·m-2)-5.4e33/(C·m-2)15.8

表2 硅橡脆材料参数

表3 环氧树脂材料参数

图4 2种结构的电导曲线

分别读取2种基元在谐振频率点的振动模态,图5表示了2种不同复合材料位移量的大小。从图5a)给出的1-1-3型压电基元的振动模态可以看出,压电陶瓷柱的振动位移最大,并且带动着周边的硅橡胶做受迫振动,而与硅橡胶相连的环氧树脂的位移接近于零。这是由于硅橡胶有着相对较小的杨氏模量,这就使得压电陶瓷柱近似自由振动。而从图5b)给出的加匹配层的1-1-3型压电基元的振动模态可以看出,位移最大值仍然出现在压电陶瓷柱的端点处。与发射端相连的梯形匹配层随着压电陶瓷振动而振动。

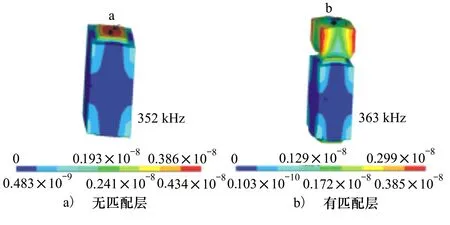
图5 1-1-3型复合材料振动模态

图6给出了2种基元顶点中心处最大位移随频率变化曲线对比。从图中可以看出,当驱动电压同为1 V时,1-1-3型复合材料基元,陶瓷柱在谐振点的最大位移为4.34×10-9m。而对于带有梯形匹配层的1-1-3型复合材料基元,其匹配层上表面的振动位移最大值为2.78×10-9m。可见无匹配层的复合材料最大振动位移为带匹配层材料的1.56倍。但采用梯形结构匹配层后,振动的有效辐射面积由压电陶瓷柱的截面积1.7 mm×1.7 mm增加为匹配层上表面的截面积2.8 mm×2.8 mm,因此有效辐射面积增大了2.7倍。根据点源叠加原理,当面积增大的比例大于振速降低的比例时,远场声压就会提高,因此此结构可以提高复合材料的发送电压响应。

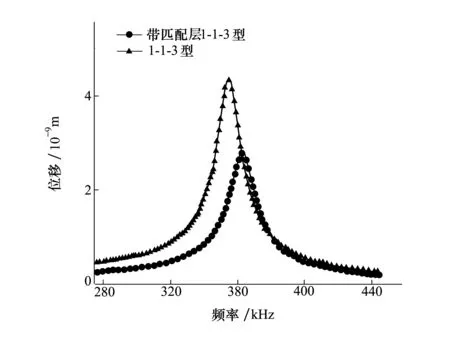
图6 复合材料位移曲线对比

3 压电复合材料制备与测试

本文研制的压电复合材料采用切割填充的方法。实验过程示意如图7所示。

图7 制备工艺流程图

首先将环氧树脂块切割打磨成25 mm×25 mm×3.9 mm大小,然后使用大族激光GMA-1390雕刻机(大族集团,中国)在环氧树脂块上切割大小为2.2 mm×2.2 mm的正方形孔。两孔间隔0.6 mm,依次完成打孔。将陶瓷块切割成1.7 mm×1.7 mm,2个陶瓷柱间隔为1.1 mm的陶瓷骨架。然后将环氧树脂框架放入陶瓷骨架中,将硅橡胶倒入陶瓷柱与环氧树脂框架之间的缝隙中,放入真空箱中抽真空排除气泡。室温固化12 h,去基底,清洁表面,用磁控溅射仪在复合材料表面溅射2 μm厚的银电极形成1-1-3型压电复合材料。最后,将用做匹配层的环氧树脂加工成下表面为梯形的结构,并用环氧树脂粘接在1-1-3型压电复合材料表面。

为了对比分析添加匹配层的1-1-3型压电复合材料的性能参数,分别制备了3块25 mm×25 mm×3.9 mm的1-1-3型压电复合材料以及3块添加匹配层的1-1-3型的压电复合材料,样品尺寸参数见表4，其中压电柱尺寸为1.7 mm×1.7 mm。

表4 2种1-1-3型压电复合材料样品尺寸参数表

利用Agilent 4294A阻抗分析仪(Agilent Technologies Inc. USA)测量了相同尺寸大小的1-1-3型以及添加匹配层的1-1-3型压电复合材料在空气中的串、并联谐振频率、Q值、带宽等参数,机电耦合系数kt可由下式计算得到:

式中的fs与fp分别为材料的串、并联谐振频率。2种材料样品电学性能如表5所示,从表中数据可以看出,1-1-3型压电复合材料谐振频率为349 kHz,带宽为8.7 kHz,机电耦合系数达到了0.698。而添加匹配层后,复合材料的谐振频率提高到362 kHz,带宽为11.2 kHz,机电耦合系数也相应降低,平均降低幅度为3%。

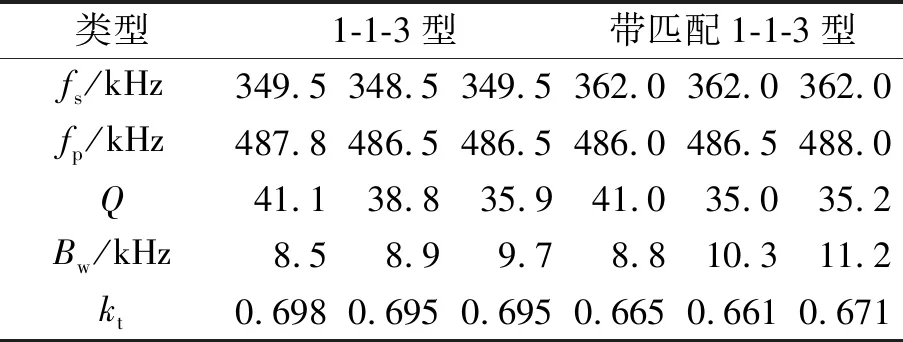
表5 2种1-1-3型压电复合材料样品的电学性能

4 换能器制作与性能测试分析

本文应用上述2种压电复合材料制备了水声换能器,其内部结构如图8所示,换能器内衬采用吸声效果更好的硬质泡沫塑料。金属上端盖采用铝,用环氧将金属端盖、背衬、压电材料以及环氧树脂匹配层固定,然后将压电复合材料上焊接的引线连接到输出电缆上,最后将其放入灌注模具中用聚氨酯灌封。图9为灌封后的换能器实物图。换能器实际尺寸是35 mm×35 mm×25 mm。

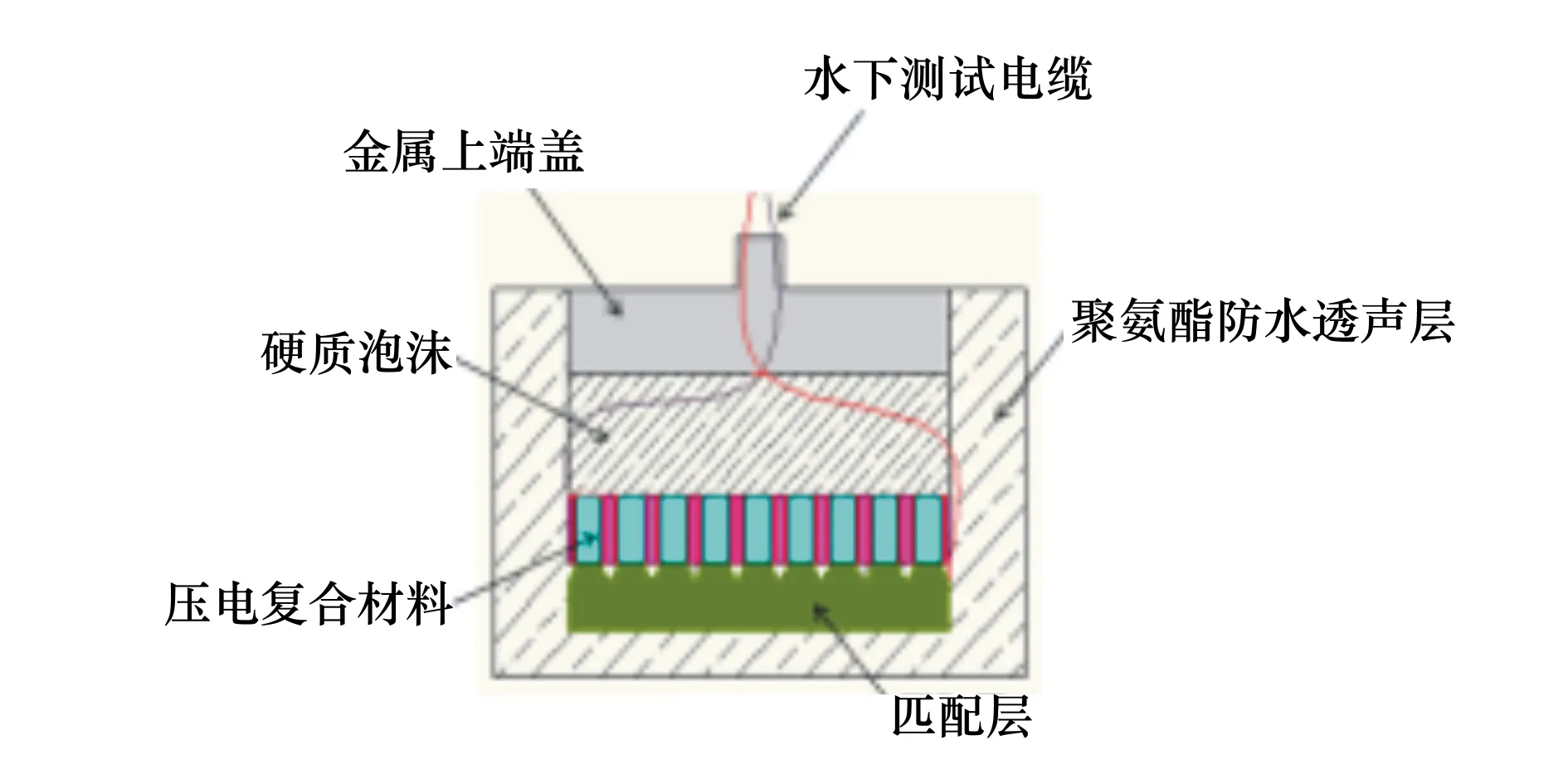
图8 换能器结构示意图

图9 换能器实物样品图

经实验测量得到2种压电复合材料换能器在水中的发送电压响应、灵敏度曲线以及声源级曲线,由于换能器各项性能相似,相对偏差均在3%以内。现选取各自其中一只换能器性能进行分析,其发射电压响应随频率变化曲线如图10所示。从图中可以看出,1-1-3型复合材料换能器在谐振频率350 kHz时发送电压响应达到最大为166 dB,添加梯形匹配层的1-1-3型复合材料换能器在谐振频率为360 kHz时发射电压响应最大为169.8 dB,比1-1-3型复合材料换能器提高了3.8 dB。这是由于在复合材料发射端添加梯形匹配层后,复合材料的振动位移减小,但是1/4波长匹配层将每个陶瓷柱的自由振动转变成整个匹配层上表面的振动,增大了辐射面积。另一方面,1/4波长匹配层可以减小声传输损耗,提高声传输特性。根据点源叠加原理,远场声压为辐射面振动速度对面积的积分。而在频率相当的情况下,辐射面振动速度又正比于振动位移,所以当面积增大的比例大于振速降低的比例时,远场声压就会提高,因此提高了发送电压响应。

如图11所示,1-1-3型复合材料换能器在谐振频率为400 kHz时接收灵敏度达到最大为-188.3 dB。添加梯形匹配层的复合材料换能器的接收灵敏度趋于平缓,在谐振频率为400 kHz时最大为-190 dB。接收情况下的-3 dB带宽达到70 kHz,大于1-1-3型复合材料的45 kHz。添加匹配层的复合材料接收灵敏度略有下降。

图12给出了声源级曲线。图中虚线a表示添加匹配层的1-1-3型换能器在谐振频率360 kHz的声源级拟合曲线,虚线b表示1-1-3型换能器在谐振频率350 kHz的声源级拟合曲线。

图10 换能器发射电压响应曲线 图11 换能器接收电压灵敏度曲线图12 换能器声源级曲线

如图12所示在相同的峰-峰值电压驱动下,加匹配层的复合材料换能器的声源级要明显高于不加匹配层复合材料换能器的声源级。1-1-3型压电复合材料换能器在峰-峰值电压为900 V时声源级达到201.8 dB,添加匹配层的换能器在峰-峰值电压为870 V时声源级达到208 dB。我们知道,当压电材料上施加的电压较小时,压电材料的应变与所加载的电压呈线性关系,当电压逐渐增加时,会出现非线性。由图中曲线可以看出,压电换能器的声源级与电压关系也表现出相同的趋势。这是因为换能器声源级与压电材料声辐射面的振速相关,而振速又与压电材料应变相关。基于以上原因本文认为峰-峰值电压小于200 V时,换能器的声源级与电压存在线性关系,当所加峰-峰值电压超过200 V后,2个换能器的声源级曲线均出现了非线性。本文分别选用200 V以下数据点进行线性拟合,2个换能器的声源级曲线分别拟合为y=0.0584x+186.85,y=0.057 5x+182.70。表6给出了换能器声源级在不同驱动电压下拟合值、测量值、相对偏差以及线性度的计算结果。从表中数据可以看出峰-峰值电压超过200 V后,2条声源级曲线的实测差值逐渐增大到6.7(±0.5) dB。由线性度(非线性误差)参数可知,添加梯形结构匹配层的1-1-3型换能器声源级线性度参数小于1-1-3型换能器声源级曲线线性度(非线性误差)。该值越小,说明曲线的线性特性越好。可见梯形匹配层的引入,不但增大了换能器的发射响应,提高了声源级,还进一步提高了声源级曲线的线性特性。

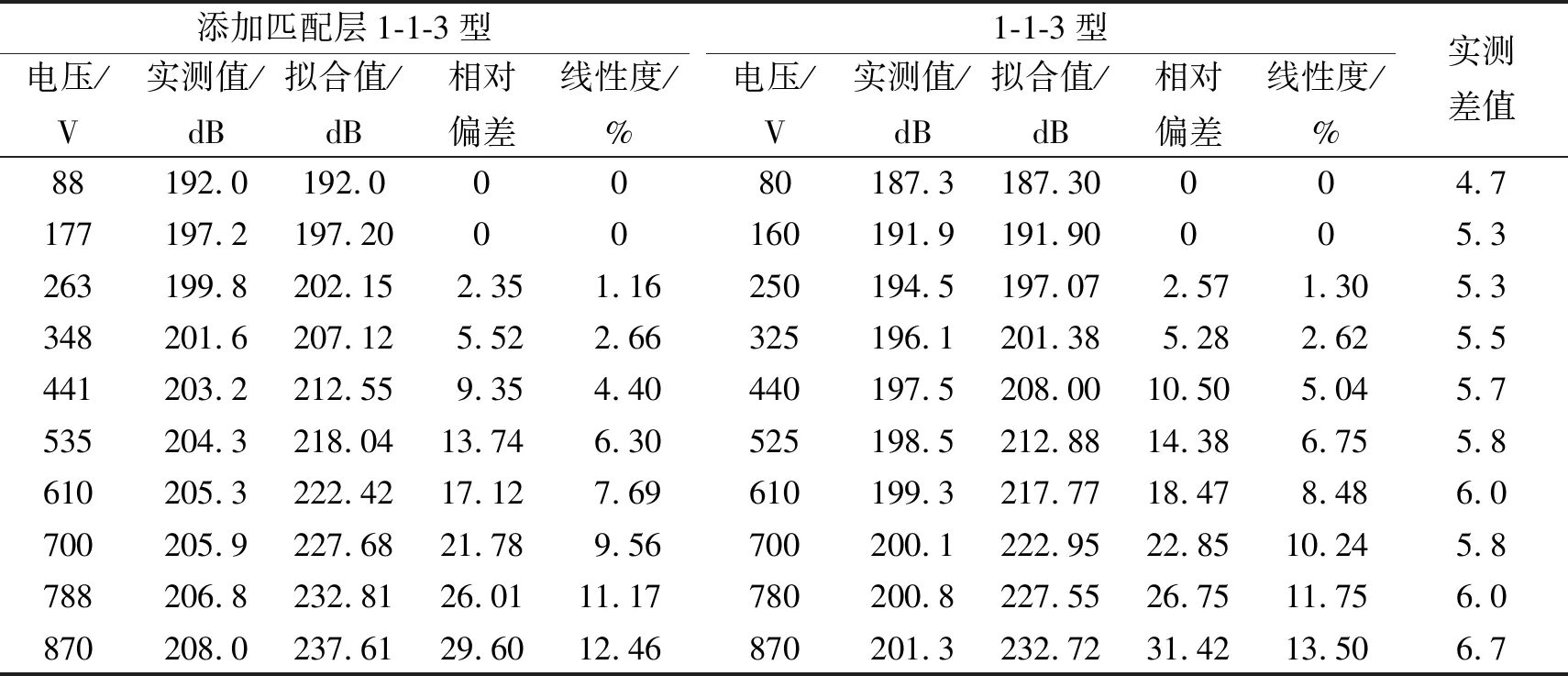
表6 声源级曲线拟合参数与实测值对比

5 结 论

本文研究的加梯形匹配层的1-1-3型压电复合材料换能器,通过在复合材料表面粘接梯形匹配层,最后用聚氨酯灌封而成。通过仿真与实验分析了2种复合材料的振动模态,仿真结果表明,加梯形匹配层的复合材料振动位移相比1-1-3型复合材料振动位移下降了1.56倍,但其辐射面积增大了2.7倍,当频率相当时,面积增大的比例大于振速降低的比例时,远场声压就会提高,益于提高发送电压响应,实验结果表明,加梯形匹配层的复合材料换能器的发送电压响应提高了3.8 dB、声源级提高了6 dB,接收带宽提高1.45倍。