高铁盐渍土地区溶陷特性的预测模型及因素敏感性分析

刘梦瑶,冯怀平

(石家庄铁道大学土木工程学院,石家庄 050043)

1 概述

近年来，中国将重建横贯欧亚大陆的“丝绸之路经济带”，作为“一带一路”的核心内容之一，以高铁为主的铁路建设变得愈加重要。然而在西北地区的高速铁路建设过程中遇到了大量盐渍土地基[1]，盐渍土是指地表以下1 m以内易溶盐含量大于0.5%的土，西北地区是我国主要盐渍土分布地区，约占全国盐渍土总面积的60%左右[2]，分布面积日趋增大。盐渍土在干燥状态下，土中易溶盐颗粒以结晶形式与土颗粒胶结在一起，土体的强度和变形模量很高。因此，常规地基的处理方法，如强夯、灌浆法等对地基处理效果不太明显[3]；盐渍土地基浸水后，易溶盐与土颗粒形成的胶结晶体溶解[4]，在上部压力作用下会产生较大的溶陷变形。可以看出，盐渍土的变形问题严重危害着对工后沉降等级要求极高的高速铁路[5]。

关于盐渍土溶陷问题，国外学者Kazi[6]、Li[7]、Stipho[8]、Dhowian等[9]先后针对中东地区(特别是沙特阿拉伯地区)的含盐砂土和黏土的物理力学性质以及含盐土与水的关系进行了大量的试验探究；Nixon和Lem[10]研究了冻土地区的盐渍土溶陷变形和蠕变特性。国内学者程东幸等[11]通过现场浸水溶陷试验，发现含盐量和含水量会影响溶陷特性，粗颗粒的含量、密实度及渗透系数也是影响溶陷性的重要因素；冯忠居等[12-17]通过室内溶陷试验发现盐渍土溶陷与初始含水量，含盐量，干密度，外加荷载，浸水时间，颗粒大小等有关，且受地域的影响较大，即不同地区的盐渍土的工程特性不尽相同；杨晓华等[18]对盐渍土地基的溶陷性进行了离心模拟试验，试验模拟了在最佳含水量的情况下，向天然盐渍土中人为加入氯盐，研究其溶陷变形在不同含盐量情况下的变化。但是，在多因素影响下对盐渍土溶陷变形的客观经验性判定公式以及影响溶陷变形的因素敏感性方面研究相对较少。

本文针对兰新铁路第二双线路基盐渍土，使用基于普通固结仪工作原理基础上改进的测试仪器，在单因素溶陷试验结果的基础上，采用正交设计方法进行多因素溶陷试验，建立发生病害地段盐渍土的溶陷变形预测模型，并探究影响此地区盐渍土地基溶陷的敏感参数。

2 试验概况

2.1 试样基本性质及土样制备

图1 试验用土粒径级配曲线

试验用土的易溶盐含量见表1，病害发生处的盐渍土属于强氯盐渍土，且氯盐极易溶于水，有很强的吸湿性，是造成盐渍土溶陷变形的主要易溶盐成分。但由于取样样本的针对性较强，无法准确判断该地区盐渍土的盐渍化程度。为了扩大研究的应用范围，本文采用室内配置盐渍土的方式研究NaCl含量对溶陷特性的影响规律。

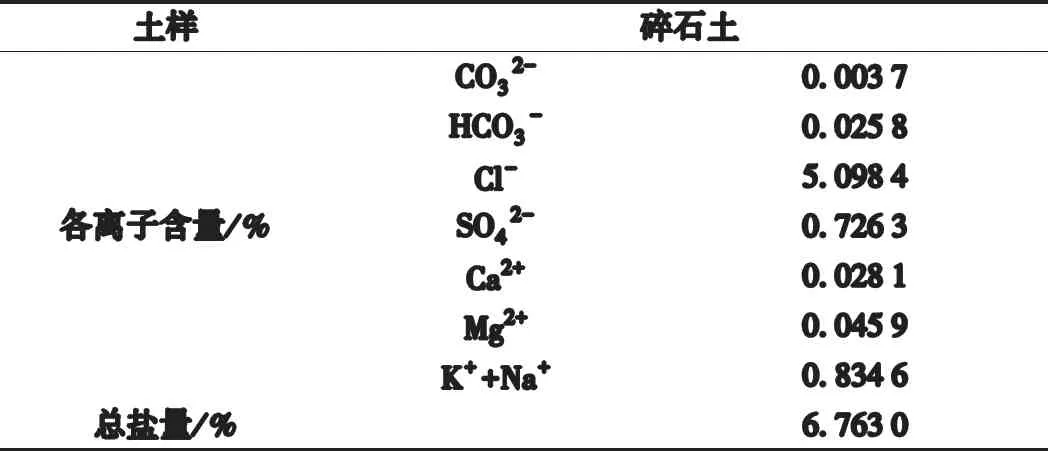
表1 天然盐渍土试样中易溶盐各离子含量

制备土样：依据设计的初始含水率、压实度、含盐量进行配置烘干后的土；置于土样制样器中，制成高度为40 mm，直径为61.8 mm的圆柱试样；随后将制备好的试样放置在保湿器中，静置48 h以上，每隔12 h翻转一次，保证试样中水分均匀，同时也为盐渍土的结晶盐产生胶结作用提供必要的时间。配置不同含盐量的盐渍土的具体步骤如下：

(1)洗土，用蒸馏水对试验用土反复淋洗和滤除，测试洗土完毕之后的土体电阻率，电阻率极大，说明土中易溶盐离子基本洗净；

(2)过筛，将上述洗土、风干后的土样进行过5 mm筛(过大的颗粒对溶陷变形影响很小)；

(3)NaCl处理，将纯NaCl颗粒进行再研磨；

(4)按照试验方案，进行土样配置(土样与NaCl充分混合，静置7 d)。

2.2 溶陷试验仪器

盐渍土在竖向荷载下，可溶解盐溶解，土体承载力降低，产生较大的溶陷变形。侧限压缩试验(固结试验)通常在普通固结仪完成。然而，普通固结仪通常采用20 mm高的环刀样。试样高度限制溶陷变形的范围，为增加研究较大的溶陷变形，需要加高试样高度。此外，固结试验通常为土样排气排水，而针对盐渍土浸水为相反的过程，所以有必要对补水测量装置进行一定改进。

本研究基于普通固结仪原理针对上面两点不足进行修正设计(图2，图3)。保证试验能准确反映盐渍土压缩特性以及溶陷特性的基础上，满足结构简单，可靠性高的要求。综上，本装置需要6个重要的部分：(1)足够高的土样盛放装置同时保证刚度非常高；(2)盛放土样装置下方应当带有透水的底座，双向保持通畅；(3)进水装置；(4)竖向加载装置；(5)保留空间，安装电子数据采集装置；(6)配套人工度数装置，与电子自动采集装置相互验证。

图2 溶陷测试仪器结构示意

图3 溶陷测试仪器实物

3 单因素试验方案及结果分析

3.1 单因素试验方案

本试验是运用正交回归的分析方法，预测盐渍土在3个因素(轴向压力p、含盐量s、压实度k)的影响下的溶陷性的简化模型。通常用溶陷系数来评价盐渍土的溶陷性，溶陷系数越大，盐渍土的溶陷性越大，溶陷系数的具体计算表达式为

式中δ——溶陷系数；

hP——浸水前，土样加至最后一级压力，下沉稳定后的高度，mm；

h0——试样的初始高度，mm。

为了确定正交试验中各因素中的具体水平参数，需要对盐渍土在单因素作用下的溶陷系数进行分析，因此设计的单因素的试验方案如下：(1)土样的压实度k设定为0.89，轴向压力F设定为150 kPa，研究盐渍土含盐量s分别为0%，2%，4%，6%，8%的情况下，溶陷系数的变化情况；(2)仅变化压实度k(0.85，0.87，0.89，0.91，0.93)，观察土样溶陷系数在含盐量s为6%，轴向压力p为150 kPa时的变化情况；(3)研究轴向压力p(50，100，150，200，250 kPa)对溶陷系数影响，土样含盐量s设定为6%，压实度k设定为0.89。

3.2 试验结果分析

根据3.1中所设定的试验方案进行试验，分别得到盐渍土溶陷系数与压实度、含盐量、轴向压力的关系曲线，如图4～图6所示。

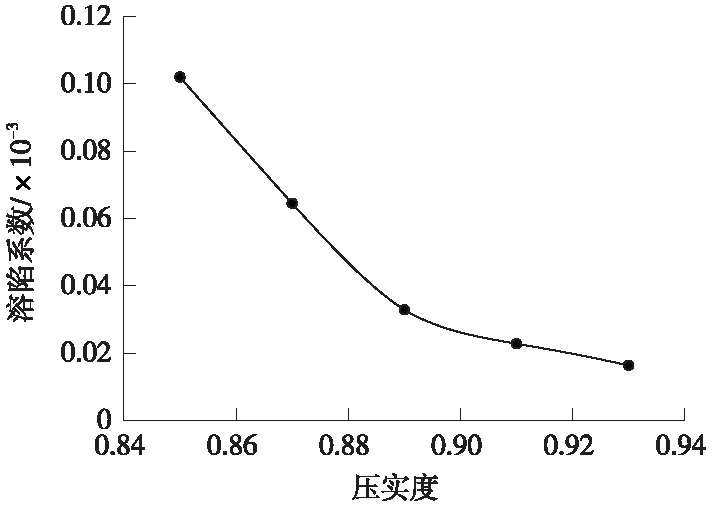
图4 溶陷系数-压实度关系曲线

图5 溶陷系数-含盐量关系曲线

由图4可知，盐渍土溶陷系数随压实度的增加而减小。压实度越小，试样的孔隙比越大，孔隙数量越多，试样内部可形成多条连续的孔隙通道，浸水后，孔隙通道塌陷，试样产生的变形越明显。

由图5可知，盐渍土溶陷系数是随含盐量的增加而增加。土颗粒与结晶盐构成了土体的骨架，而浸水过程基本上破坏了试样中土颗粒与易溶盐晶体的胶结作用，使试样内部原来占据结晶盐的位置都变为孔隙，在压力的作用下，土粒重新排列，并被压缩。含盐量越大，被水分破坏的胶结点数量越多，试样中形成的孔隙也就越多，试样的溶陷变形也更为显著。

图6 溶陷系数-轴向压力关系曲线

由图6可知，盐渍土溶陷系数是随轴向压力的增加而增加。轴向压力的作用，使得土颗粒在水分的润滑下更易于滑落和重新排列，密实度提高。轴向压力越大，这种作用愈加明显，但随着压力的不断增大，试样内的孔隙也在不断减小，土颗粒滑落的阻碍增大，使得溶陷系数的增幅逐渐减小。

通过上述3个单因素试验可以看出，在含盐量，压实度，轴向压力的影响下，溶陷系数呈良好的线性变化。这样的试验结果有利于溶陷系数的正交回归分析中参数的选择。

4 盐渍土溶陷变形预测模型

4.1 正交试验设计与结果

为了给盐渍土地区溶陷性提供参考，根据单因素试验结果，设计正交回归试验[19-20]，由于下星号臂值低于下水平，所以下水平选定含盐量为2%，三个因素的水平选择见表2。

表2 试验因素水平

4.2 溶陷变形预测模型

根据正交回归原理得出溶陷系数的二次正交回归设计计算(表3)。

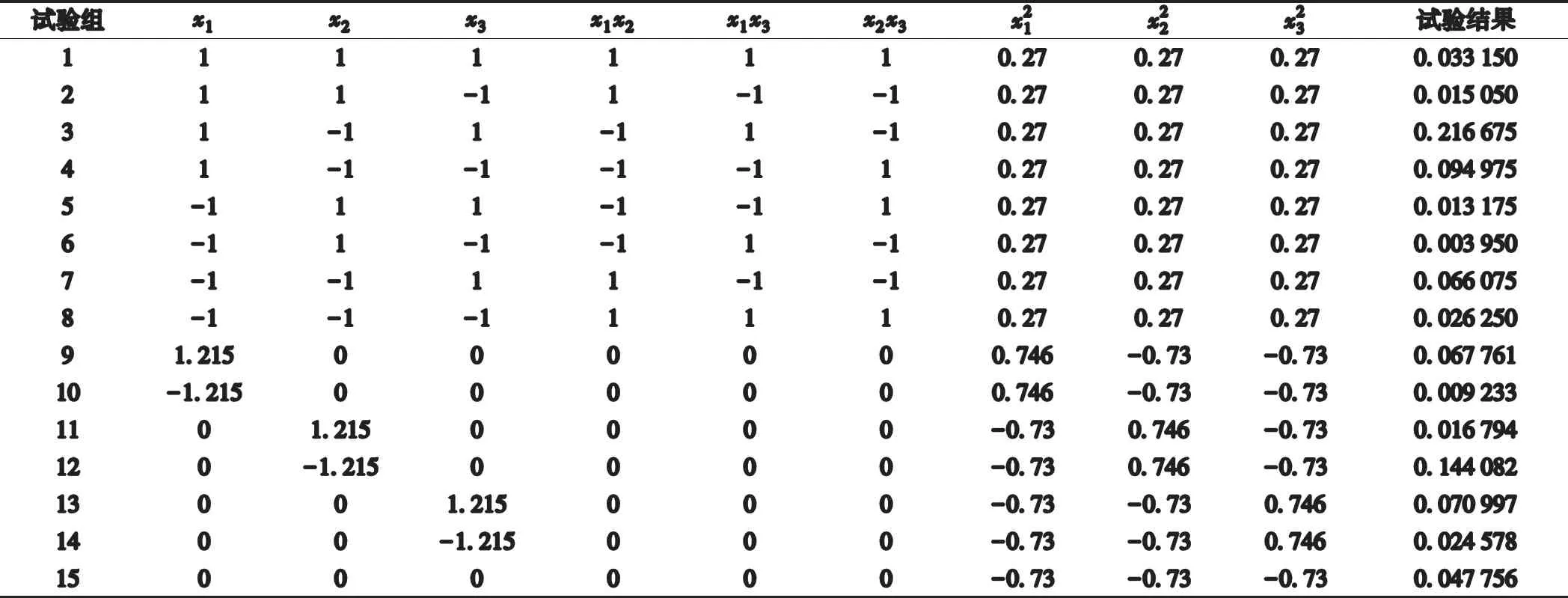
表3 二次正交回归试验设计

Y=0.057+0.029x1-0.045x2+0.022x3-

(1)

根据正交试验的设计原理可知，式(1)中各因素之间存在正交性，所以单纯删除其中的某项并不会影响其他因素系数的变化。将不显著因素的偏回归平方和归入到残差平方和之中，对简化之后的方程再进行一次方差分析得表5。

表4 试验方差分析I

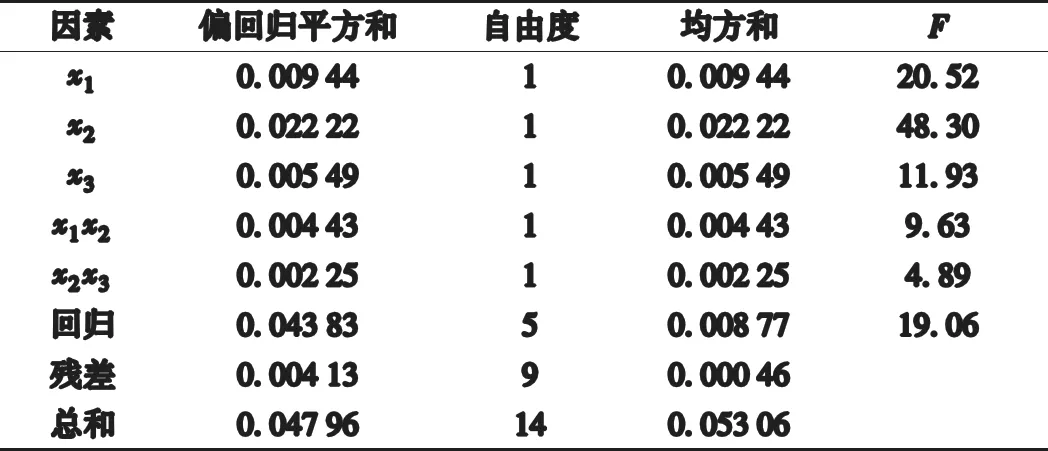
表5 试验方差分析Ⅱ

简化之后的方程为

Y=0.057+0.029x1-0.045x2+0.022x3-

0.023x1x2-0.017x2x3

取显著性水平α=0.05，F0.05(5，9)=3.48，F0.05(1，9)=5.12。表5分析结果F0.05(5，9)=3.48< 19.06可知，回归方程达到显著性水平，方程有意义。但是，在此回归式中压实度与含盐量的交互作用x2x3所得回归系数的显著性水平小于F0.05(1，9)=5.12，回归系数未达到显著性水平。因此，将x2x3项的偏回归平方和归入到残差平方和中，重新对所得的方程进行一次方差分析得表6，得到新的回归方程：

Y=0.057+0.029x1-0.045x2+0.022x3-0.023x1x2

R2=0.867

(2)

取显著性水平α=0.05，F0.05(4，10)=3.48，F0.05(1，10)=4.96。由分析F0.05(4，10)=3.48<13.70回归方程达到显著性水平，方程具有意义，x1，x2，x3，x1x2的回归系数均大于F0.05(1，10)=4.96，则这4个因素均达到显著性水平。

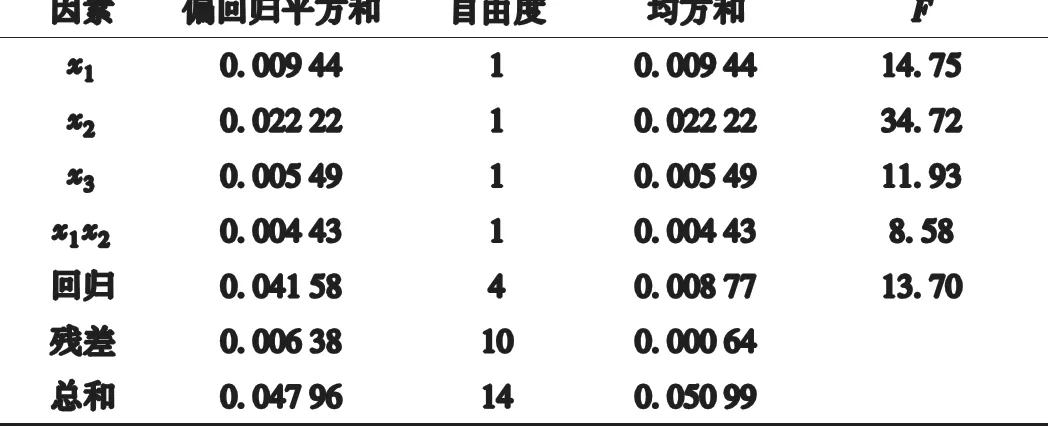
表6 试验方差分析Ⅲ

构造新的F值统计量，即

式中，R1与R2分别为式(1)与式(2)的复相关系数；k1与k2分别为式(1)与式(2)的自变量个数；F值服从k1-k2和n-k1-1个自由度的F分布。计算可得F=5.045

Y1=0.125 2+0.180 3z1-0.167z2+

0.000 176z3-0.192z1z2

式中，Y1表示盐渍土实际溶陷系数；z1表示因素实际含盐量；z2表示因素实际压实度；z3表示因素实际所受轴向压力；z1z2表示实际含盐量与压实度的交互作用。

4.3 盐渍土的溶陷性敏感因素分析

运用SPSS分析软件，采用逐步回归方法对所剩4个显著性因素进行分析，构建显著性模型，具体见表7。

表7 模型汇总

注：模型1预测变量为常量、压实度；模型2预测变量为常量、压实度， 轴向压力；模型3预测变量为常量、压实度、轴向压力，含盐量；模型4预测变量为常量、压实度、轴向压力、含盐量、含盐量与压实度的交互作用。

R2为决定系数，所表示的是所预测的溶陷系数模型能够解释因变量所占比重。由表7可知，模型1是由常数项与压实度所构建的模型，R2=0.463，调整之后的R2=0.422，可知压实度是影响盐渍土溶陷系数的最主要因素。由R2更改量可知，影响盐渍土溶陷系数的敏感性因素由高到低依次为：压实度、轴向压力、含盐量以及轴向压力与压实度的相互作用，影响所占比重分别为0.463，0.172，0.140，0.092。轴向压力与压实度的相互作用在这里出现的原因是轴向压力对测试土的压实度产生了影响，从而影响到了盐渍土溶陷情况。

4.4 对比分析

为了验证此模型在盐渍土地区的实用性，将文献[21]的罗布泊强氯盐渍土中的数据提取并代入公式中进行验证。

首先采用氯盐渍土的含盐量，压实度为定值，溶陷系数随轴向压力变化而变化。本试验盐渍土的含水率为8%，文献[21]中盐渍土含水率为13%。由于含水率的不同，在试验的初始阶段以结晶体的形式存在的易溶盐晶体的溶解的量不同，对土体结构破坏情况也不同，所以造成的初始溶解系数不同，且张洪萍等[13-14]研究表明初始含水量较小时，溶陷系数更大。因此，在对比分析过程中将2组数据初始溶陷系数设定为相同值，即将预测模型所得直线截距降低，向下平移，再进行对比。根据图7的观察可以发现，预测模型中溶陷速率变化与文献[21]的试验数据所得溶陷速率较为相似，且预测模型所得结果与参考的试验数据也相差不大，可为工程实践提供参考。

图7 数据对比

5 结论

基于普通固结仪原理，优化设计一种新的测试仪器，能更充分、直观地测试盐渍土试样溶陷变形；以兰新铁路第二双线出现的盐渍土溶陷病害为背景，运用SPSS分析软件，采用正交回归设计原理，得出了在多因素交互作用下的盐渍土溶陷变形规律及盐渍土地基溶陷变形公式，分析了高速铁路盐渍土地基溶陷变形控制的敏感因素。所得结论如下。

(1)试验所得公式具有较高的计算精度，不仅为长期宏观预测兰新铁路第二双线盐渍土地基溶陷变形发展规律提供了便利，且对其他高速铁路盐渍土地基工程具有一定参考价值。

(2)针对压实度、轴向压力与含盐量进行回归分析得到预测模型，并分析这三个因素的敏感性。试验结果表明影响盐渍土的溶陷系数的敏感性因素由高到低依次为压实度、轴向压力、含盐量以及轴向压力与压实度的相互作用。

(3)试验结果所得溶陷变形预测模型是基于氯盐的高速铁路盐渍土地基，对于盐渍土地区高速铁路地基施工方案的设计、病害的预防及处治等均具有参考意义。