一种面向多源异构数据的协同过滤推荐算法
吴 宾 娄铮铮 叶阳东
(郑州大学信息工程学院 郑州 450001)
随着互联网和信息技术的迅猛发展,在电子商务、电子旅游和社交网站等诸多领域都存在着海量数据,“信息过载”日益严峻.如何快速而精准地从浩瀚的数据海洋中帮助用户获取有价值的信息已成为学术界和工业界亟待解决的问题.尽管传统的搜索引擎技术一定程度上能够满足用户的需求,却无法向用户主动提供个性化的服务.在此背景下,推荐系统的出现被认为是缓解此问题的重要工具,它通过收集和分析用户的历史行为信息,从而向用户提供可能感兴趣的服务.在众多推荐算法中[1],协同过滤[2]因其简单高效而广受各商业网站的青睐,如Netflix的电影推荐、今日头条的新闻推荐等,它不仅改善了用户的体验且为企业带来了可观的商业价值[3].
与电影、新闻等领域的推荐系统不同,用户的购买决策过程或对某物品的评分往往受多种因素所致,如图1所示.1)物品的替代关系:用户在购买某一物品时往往会同时浏览或点击不同品牌下的同种物品,这些物品在功能上具有可替代性;2)物品的互补关系:如果某一物品与特定的物品经常被用户一起购买,则这两者在功能上存在较强的互补关系;3)物品的视觉信息:用户在购买或评分某物品时会受到其色泽、风格等视觉信息的影响.
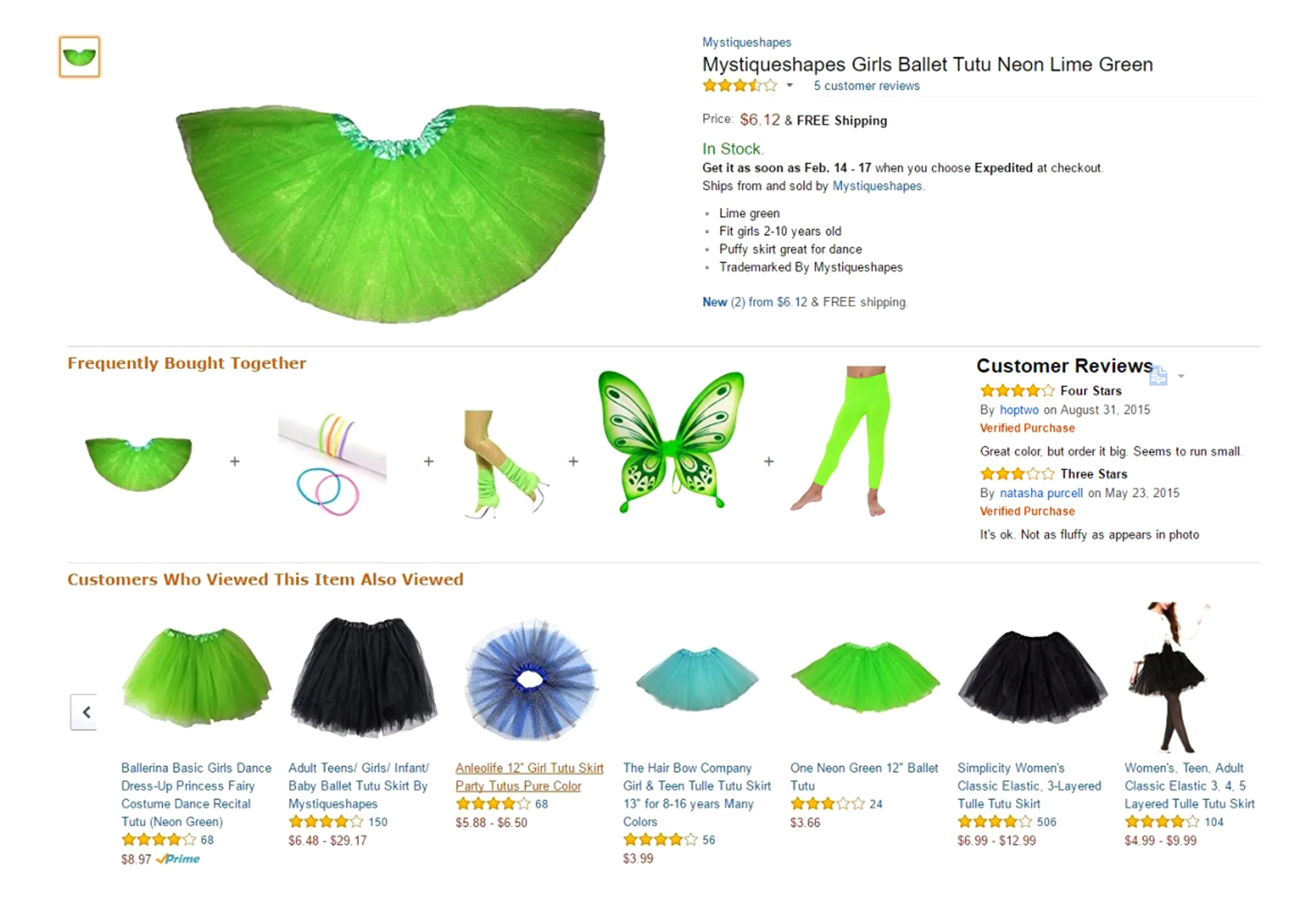
Fig. 1 An example of online shopping services图1 一个在线购物案例
当前的推荐算法虽一定程度上能够缓解数据稀疏、冷启动等问题,在面对上述场景进行评分预测时却存在3个问题.
1) 新物品的评分预测.由于新物品刚被加入系统,可使用数据较少,如何预测用户对新物品的喜好.
2) 单一类型数据的融合.如何根据数据自身所具有的特点将其融入已有推荐模型.
3) 多源异构数据的整合.如何有效整合多源异构数据来实现数据的价值最大化是当前推荐系统面临的最大挑战.
由于这3个问题的存在,使得已有协同过滤算法在电商网站上的推荐精度有待进一步提升.
为了解决这3个问题,本文首先对多源异构数据下各类数据进行了形式化定义.进一步,详细分析了用户的评分与物品的替代关系及互补关系的相关性.最后,根据各类数据的特点为其设计了不同的融合方式,并提出一种可应用于多源异构数据环境下的推荐模型.
本文的主要贡献有3个方面:
1) 在大数据的环境下,研究了推荐系统在面向多源异构数据时所需解决的评分预测问题;
2) 对多源异构数据中各种类型数据给出明确定义,并分析了物品的2种关系数据与用户评分之间的相关性;
3) 提出一种融合多源异构数据的矩阵分解模型,设计了一种高效的算法MSRA(multi-source heterogeneous information based recommendation algorithm) 用于求解所提模型的参数,并详细分析了该算法的时间复杂度.
为验证MSRA算法的性能,在电商网站Amazon的真实数据集上,本文算法与多个主流的推荐算法进行了大量的对比.实验结果不仅验证了本文设计的融合多源异构数据方法的合理性,而且表明所提出算法能够有效预测不同类型物品的实际评分,尤其可以预测目标用户对新物品的喜好.
1 相关工作
与本文相关的工作主要包括3个方面:1)传统的矩阵分解推荐算法;2)融合近邻关系的推荐算法;3)融合视觉特征的推荐算法.
1.1 传统的矩阵分解推荐算法
在众多传统推荐算法中,矩阵分解因具有完善的理论基础[4-5]、较高的预测精度[6-7]、良好的扩展性[8-9]等优点,而广受学术界与工业界的青睐.传统矩阵分解模型的基本思想是[5]:假设在一个购物推荐系统中存在n个物品和m个用户,对于给定的评分矩阵R∈Rm×n,寻求用户潜在特征矩阵P和物品潜在特征矩阵Q,使得两者乘积所得近似拟合R.通常可基于随机梯度下降(stochastic gradient descent, SGD)求出式(1)的局部最优解P和Q.
(1)
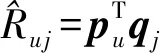

(2)
相应地,式(1)应修改为
(3)
其中,μ表示总体平均评分,bp,bq分别表示用户和物品的偏置向量.bp u,bq j分别表示用户u和物品j的评分与μ的偏差,θ={pu,qj,bp,bq,yk}.每个物品k关联一个隐式反馈向量yk,用于建模隐式反馈信息对用户u的潜在特征向量的影响.
传统的矩阵分解推荐算法虽基于历史评分信息可以预测特定用户对某物品的偏好,但仅使用单一的评分信息而使其面临着数据稀疏、冷启动等问题.信息网络的普及为获取用户(物品)的近邻关系提供了便利条件,如何融合这些近邻关系来提高推荐算法的预测精度成为众多研究者的关注点.
1.2 融合近邻关系的推荐算法
传统的矩阵分解模型通常潜在地假设用户之间相互独立,因而忽略了用户之间的内在联系.在传统矩阵分解模型之上融合用户的近邻关系[10-11],不仅可以丰富单个用户的信息,而且能更好地对各用户进行建模.郭磊等人[12]将用户之间的信任关系强度融入概率矩阵分解模型(probabilistic matrix factorization, PMF)设计了一种信任关系强度感知的推荐算法.Ma等人[13]基于用户的社会关系信息设计了社会正则化,并将其用于约束PMF的目标函数,进而提出SoReg算法.Jamali等人[14]将社交网络中的信任传播结构与PMF结合提出SocialMF算法,该算法同时考虑了直接和间接信任关系对目标用户喜好的影响.在众多社会化推荐算法中,Guo等人[15]提出的TrustSVD推荐算法因同时考虑了信任关系对目标用户兴趣的显式和隐式影响,使得该算法在评分预测任务上取得了较好的效果.TrustSVD算法中对未知评分的预测为

(4)
相应地,基于式(4)对式(3)改进后的目标函数为

(5)

在真实商业场景中,除了融合社会关系之外[16],已有不少工作通过考虑物品的近邻关系来提升评分预测精度.文献[17]基于评分的时序信息同时构建物品和用户的近邻关系,然后将两者融入PMF中提出基于时序行为的推荐算法SequentialMF.文献[18]基于标签信息来构建物品和用户的相似性关系,并将两者融入PMF中提出基于近邻的概率矩阵分解模型.文献[19]基于物品的属性信息来获取物品的相似性关系,并将其与用户的社会关系相结合,提出图正则权重的非负矩阵分解模型.上述工作通过借助辅助信息来获取用户(物品)的近邻关系,一定程度上提升了传统推荐算法的精度,但如何预测用户对新物品的喜好依然有待解决.
1.3 融合视觉特征的推荐算法
近些年,随着深度学习在图像识别、语音识别等领域取得巨大成功[20-21],众多学者开始尝试如何使用深度学习提取物品的视觉特征与当前的推荐模型相结合并用于推荐系统的物品排序任务;He等人[22]使用卷积神经网络(convolutional neural network, CNN)[23]提取物品的视觉特征并将其以线性嵌入的方式与贝叶斯个性化排序算法(Bayesian personalized ranking, BPR)[24]结合提出融合视觉特征的贝叶斯个性化排序算法(visual Bayesian personalized ranking, VBPR);Roy等人[25]使用CNN提取视频的特征并将其以特征转换的方式与CLiMF结合提出visual-CliMF算法,实验表明视觉特征有助于提升视频推荐的精度;Wang等人[26]认为用户向系统所上传的图片有助于提升兴趣点(point-of-interest, POI)推荐的性能,作者将提取CNN特征的VGG16模型与传统的矩阵分解模型相结合提出融合视觉特征的POI推荐框架VPOI.上述工作已经表明通过深度学习技术提取物品的视觉特征,将其与传统的推荐算法结合用于物品排序任务虽取得了成功,但如何考虑物品的视觉特征用于推荐系统的评分预测任务目前尚存较少文献探索.
2 问题描述
本节将首先定义物品推荐中5种类型的数据,然后对多源异构数据的场景下评分预测问题进行形式化描述,最后分析了物品之间的2种关联关系.
2.1 问题定义
在推荐系统中,多源异构数据通常包括结构化、半结构化和非结构化数据.其中结构化数据包括用户的显式反馈、社交网络、与物品相关的关联关系等;半结构化数据包括用户的属性信息(比如用户的年龄、地点、职业等)、物品的属性信息(物品的类别、标签等)等,这些数据可通过对其离散化或0-1化转换成结构化数据;非结构化数据包括用户的评论信息、与物品相关的图像视频等,这些数据可通过信息检索技术或机器学习方法将其转换成结构化数据.为了清楚起见,详细定义了与本文相关的5种数据.
定义1.用户的显式反馈.本文定义用户的显式反馈为评分矩阵R∈Rm×n.其中Ru j≠0表示用户u对物品j的喜好程度;Ru j=0表示用户u尚未对物品j进行评价,但并不意味着用户u不了解该物品.
定义2.用户的社会关系.用户之间的社会关系图表示为G=(U,E),其中U表示用户的集合.∀u,v∈U,(u,v)∈E表示用户u对用户v存在社会关系,每条社会关系(u,v)∈E的权重Tu v∈[0,1]表示用户之间的信任程度.但需注意的是,在大多数的社交网络中,Tu v通常取值0或1.
定义3.物品的替代关系.物品之间的替代关系图表示为G=(J,E′),其中J表示物品的集合.∀i,j∈J,(i,j)∈E′表示物品与物品之间存在替代关系,每条替代关系(i,j)∈E′的权重表示物品之间的替代程度.
在图1中,用户在购买芭蕾舞裙子时会经常浏览不同颜色、大小、商家的裙子,那么这些裙子在实用性上是可替代的,因此它们之间的关联关系可看作替代关系.
定义4.物品的互补关系.物品之间的互补关系图表示为G ″=(J,E ″).∀i,j∈J,(i,j)∈E ″表示物品与物品之间存在互补关系,每条互补关系(i,j)∈E ″的权重表示物品之间的互补程度.
在图1中,用户在购买芭蕾舞裙子时经常与手环、腿套等物品一起购买,那么裙子与这些物品之间在功能上是互补的,因此它们的关联关系可看作互补关系.
定义5.物品的视觉特征.对于给定的物品j,通常有若干个图片与之相对应,可借助深度学习中CNN的方法对物品j提取出视觉特征向量fj.
在大数据的环境下,多源异构数据通常比较复杂,规模也比较大.例如Amazon商业购物网站不仅包括用户与物品的评分信息,而且包括用户之间的社会关系、物品之间的互补关系、物品的评论和图片信息等,其用户和物品的数量、社会关系的数量、互补关系的数量往往达到千万甚至上亿的规模.如何合理并高效地将多源异构数据与传统的推荐模型相融合是当前推荐系统面临的核心问题.以下对本文所要解决的推荐问题给出了形式化定义.
问题1.评分预测.给定用户u、物品j、评分矩阵R、用户之间的社会关系图G、物品之间的替代关系图G′、物品之间的互补关系图G ″以及物品j的CNN特征fj,本文的目标是基于上述多源异构信息预测用户u对物品j的喜好程度.
2.2 数据分析
本文以Amazon数据为例,用户在进行网上购物时会浏览许多待选的商品,在对这些商品进行比较时会产生一系列的行为数据,如“同时浏览(also_viewed)”、“一起购买(bought_together)”等,并被系统存储在与用户相关的日志中.由文献[27]可知,数据中“同时浏览”信息可看作物品之间的替代关系,而数据中“一起购买”信息可看作物品之间的互补关系.本文通过分析亚马逊的4个数据集,可得出2个结论:
结论1.用户对物品的评分与物品之间的替代关系存在弱相关性.
为了分析物品之间的替代关系对用户评分的影响,本文计算了每个物品的评分与其替代关系中所有物品评分均值的皮尔逊相关系数(Pearson correlation coefficient, PCC),结果如图2所示.

Fig. 2 Substitutable relationships图2 替代关系
从图2可以得出,从单个区间来看,由替代关系所得出的相关系数取值小于0占据大部分(分别为18.57%,17.07%,17.05%,24.28%),但从整个区间来看相关系数取值大于0占据大部分(分别为81.43%,82.93%,82.95%,75.72%)且4个数据集的平均相关系数分别为0.28 61,0.302 0,0.310 1,0.336 9.因此根据上述分析可知存在替代关系的2个物品具有弱相关性,用户在评分或购买物品时受替代关系的影响较弱.
结论2.用户对物品的评分与物品之间的互补关系存在强相关性.
为了分析物品之间的互补关系对用户评分的影响,同样地可以使用PCC计算每个物品的评分与其互补关系中所有物品评分均值的相关程度,结果如图3所示:

Fig. 3 Complementary relationships图3 互补关系
从图3可以得出,从单个区间来看,由互补关系所得出的相关系数取值在区间[0.9,1.0]上占据大部分(分别为46.49%,13.27%,39.25%,45.43%)且4个数据集的平均相关系数分别为0.582 7,0.392 3,0.442 2,0.465 4.根据上述分析可知,存在互补关系的2个物品具有强相关性,因此用户在评分或购买物品时受互补关系的影响较强.
3 面向多源异构数据的推荐方法
本节将详细研究物品的替代关系、互补关系以及视觉特征对已有推荐模型的影响,然后提出一种融合多源异构数据的矩阵分解模型.
3.1 融合物品的替代关系
现实生活我们在线购物时通常会浏览不同商家的同类物品,最终会根据物品的颜色、价格、销量等来做出购买决定,正所谓“货比三家”.被用户同时浏览的物品通常在功能上是相似的,即存在替代关系.根据2.1节的结论可知,存在替代关系的物品之间在评分上具有弱相关性,因此在传统推荐模型中考虑替代关系将会有效提升推荐系统评分预测的精度.为了更准确地对物品评价信息进行建模,本文假定用户对特定物品的喜好受物品的固有特征和外在特征所影响.例如对于特定的物品j,本文使用qj来建模物品的固有特征 (如物品的类别、尺寸、重量等),使用xj来建模物品j的外在特征 (如物品的价格、销量).Qj表示与物品j存在替代关系的物品集合.受文献[28]启发,物品之间的弱相关关系可通过改进式(2)来进行建模,改进后的评分预测式:
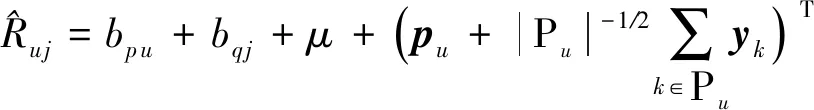
(6)
相应地,式(3)加入xt的正则项后更新为
(7)
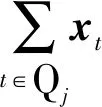
3.2 融合用户的社会关系与物品的互补关系
社交网络的普及为获取社会关系提供了便利条件,用户之间的这种关系通常具有较强相关性,合理使用该关系不仅可以丰富单个用户的信息,而且能够缓解数据稀疏、用户冷启动问题.在现实世界中,除用户拥有社会关系外,某些物品之间也存在较强的关联关系.由2.1节的结论可知,存在互补关系的2个物品与用户的评分具有强相关性,因此融合该关系将会有效缓解物品的冷启动问题.受结合社会关系方式的启发,本文在TrustSVD基础之上研究了互补关系对评分预测的影响.本节通过共享物品潜在特征矩阵Q并以联合分解[29]的方式融入互补关系,由式(5)改进后得到的目标函数式:

(8)
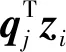
3.3 融合物品的视觉信息
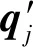
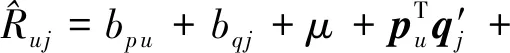
(9)

(10)
相应地,可得出融入物品视觉特征的目标函数:
(11)
其中,θ={pu,qj,bp,bq,yk,bE,E}.
3.4 融合多源异构数据的矩阵分解模型
3.1~3.2节已详细介绍如何对替代关系、互补关系、物品的视觉信息分别建模,然而现实生活中用户是否购买某物品通常受多种因素所致,仅考虑1种或2种信息很难有效对用户的兴趣进行建模.当下推荐系统亟待解决的问题是如何利用数据的关联、交叉和融合来实现数据的价值最大化,文献[30]认为解决这一问题的关键在于数据的融合.综合3.1~3.2节对不同信息源的融合方法,本节提出一种融合多源异构数据的矩阵分解模型,其示意图如图4所示:
最终的评分预测:
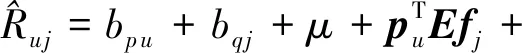
(12)
在式(8)基础之上,可得出最终模型的目标函数:
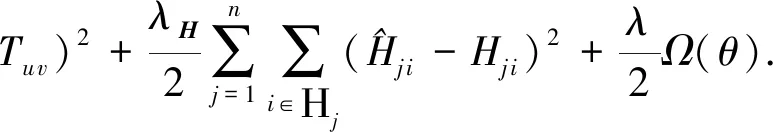
(13)
根据文献[13]的分析可知,使用自适应正则化来约束模型参数的学习更为合理.本文采用与之相似的做法,则模型的正则项可表示为
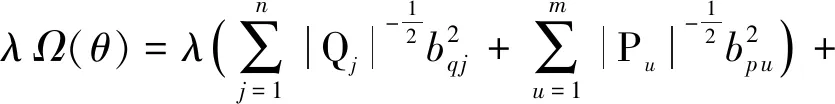
(14)
3.5 MSRA算法
本文使用SGD求解融合多源异构数据的矩阵分解模型的参数,给出MSRA算法的详细流程.
算法1.MSRA算法.
输入:T,H,Q,Rtrain,d,c,α,β,λ,η;
输出:bp,bq,bE,P,Q,Y,W,Z,E,X.
① 初始化模型参数bp,bq,bE,P,Q,Y,W,Z,E,X;
② while L不满足收敛条件do
③ 引入4个临时变量P′,Q′,W′,Z′;
④ for (u,j)∈Rtraindo

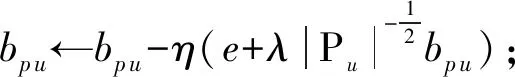
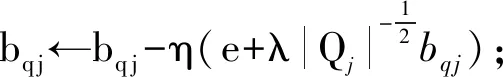
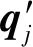
⑨ fork∈Pudo
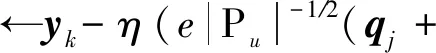
MSRA算法的时间复杂度主要包括对目标函数L和各梯度变量的计算.计算目标函数L的时间复杂度为O(d|Rtrain|+d|T|+d|H|),|T|表示社会关系数量,|H|表示互补关系的数量.计算梯度∂L∂bp u,∂L∂bq j,∂L∂bE,∂L∂pu,∂L∂qj,∂L∂yk,∂L∂xt,∂L∂wv,∂L∂zi,∂L∂E的时间复杂度分别为其中表示物品平均被评分的数量.由此可得出算法迭代一次的复杂度为由于g≪min(|X|,|T|,|H|),c一般取常数4 096,因此算法的整体复杂度与评分数量、社会关系数量、替代关系数量、互补关系数量呈线性相关,可用于处理大规模数据.
4 实验结果及分析
4.1 数据集介绍
为了验证不同类型数据对算法精度的影响,本文在Amazon数据集上进行实验和对比分析,该数据集由文献[24]的作者所提供.Amazon数据集中含有评分信息、同时浏览的物品、一起购买的物品、物品图片等.本文选取“Office_Product”,“Video_Games”,“Grocery_and_Gourmet_Food”,“Clothing_Shoes_and_Jewelry”四个类别的数据集来验证所提出的推荐算法.本文将数据集中“also_viewed”信息看作物品之间的替代关系,“bought_together”信息看作物品之间的互补关系.实验中所用数据集的统计特性如表1所示,其数据集的稀疏度根据文献[31]计算所得.

Table 1 Statistic of The Four datasets表1 4个数据集的统计特性
与He等人[22]做法类似,对每个物品选取1幅图片,然后使用Jia等人[23]所设计的caffe框架对每个物品提取视觉特征.实验中首先将拥有5个卷积层和3个全连接层的CNN方法在1.2million ImageNet (ILSVRC2010)图片上进行预训练,然后将本文数据集中的图片数据进行训练,最后选取第2个全连接层的输出作为每个物品的视觉特征,这里c=4 096.
4.2 评价指标
目前推荐系统的研究中,平均绝对值误差和均方根误差(root mean squared error,RMSE)是评分预测任务的常用评价指标.本文采用RMSE来评价推荐系统中算法的性能,RMSE通过计算预测值与真实值之间的差别来衡量推荐算法的准确性,其值越小,推荐系统的性能越好.
(15)
其中,Rtest表示测试集,|Rtest|表示测试集中用户评分数目.
4.3 实验设置
在实验中,本文基于Librec[注]http://www.librec.net库来实现各对比算法及MSRA算法.为了验证多源异构数据中不同类型的数据在推荐过程中所起的作用,本文选取了7种推荐算法与MSRA进行了详细对比:
1) UserAvg.该算法使用每个用户的评分均值对未知的评分数据进行预测.
2) SVD++.该算法是由Koren[7]提出的一种同时考虑用户偏置、物品偏置以及用户隐式反馈信息的推荐算法,其预测精度是基于矩阵分解的推荐算法中精度较高的一种,并且是当年Netflix大赛获奖者所使用的关键算法.
3) SVD_SR.该算法由SVD++融合替代关系(substitutable relationships)数据后所得,其目标函数为式(3).
4) TrustSVD.该算法由Guo等人[15]提出的一种社会化推荐算法.在对目标用户的兴趣进行预测时,它同时考虑了信任用户对目标用户的显式和隐式影响.由于本文选取的4个数据集中不包含用户的社会关系,根据文献[32-33]可知,选取目标用户的10个最相似的用户可近似代替社会关系.
5) SVD_CO.该算法通过联合分解的方式同时融合用户的社会关系和物品的互补关系所得,其目标函数如式(8)所示.
6) SVD_V.该算法通过嵌入的方式将物品的视觉特征信息融合SVD++所得,其目标函数如式(11).
7) VMCF.该算法由Park等人[34]提出的一种同时考虑物品的替代关系及视觉信息的推荐算法.
为了清楚起见,根据是否个性化(personalized, P)、是否考虑替代关系(substitutable relationships, SR)、社会关系(social network, SN)、互补关系(complementary relationships, CR)、视觉特征(visual feature, VF)对算法进行了详细的对比,如表2所示:
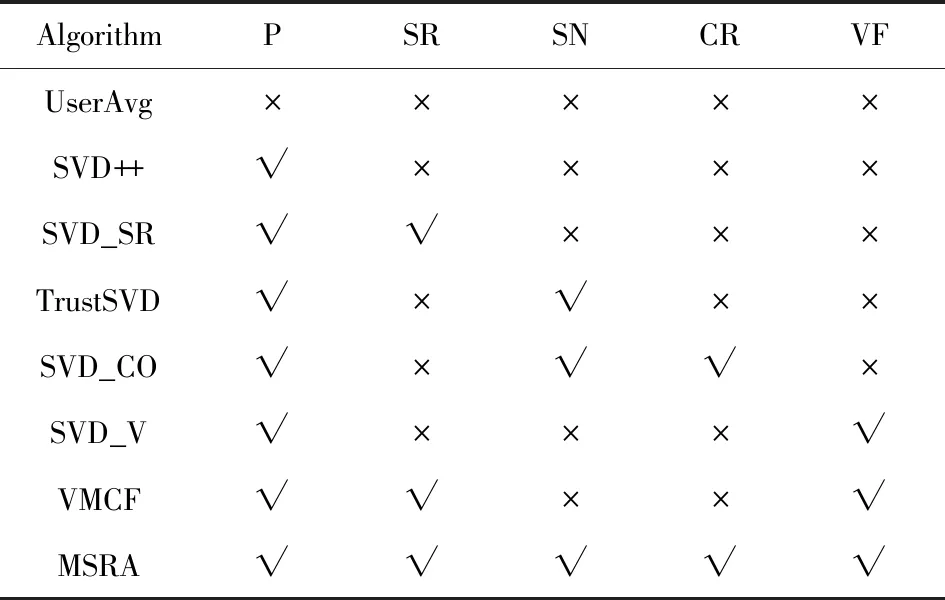
Table 2 Properties of Algorithms Being Compared表2 各对比算法的特性
Note: “√” means that the target algorithm includes the specific property, while “×” means excluding the specific property.
本文将数据集分成训练集和测试集,训练集用于学习推荐算法中的参数,测试集用于评估推荐算法的准确性.在实验中,按照4∶1的比例将4个数据集随机地分成训练集和测试集.这种随机分割数据的方式独立地执行10次,以10次运行结果的平均值作为最后的实验结果.为了公平起见,不同算法中的参数设置均为Amazon数据集上的最优设置.在SVD++和SVD_SR中,λ=0.1;在TrustSVD中,λ=0.9,λT=0.1;在SVD_CO中,λ=0.9,λT=λH=0.1;在SVD_V中,λ=0.9,λE=100;在VMCF中,λ=0.1,λS=0.3,λE=100;在MSRA算法中,λ=0.9,λT=0.1,λH=0.3,λE=100.此外,本文的所有实验均设置潜在特征向量维度d=20.实验在Windows7操作系统,64 GB内存,Intel®Xeon®CPU E5-2620 0 @ 2.00 GHz的机器上进行,实验程序基于Java语言实现.
4.4 实验结果与分析
实验1.全体和冷启动物品集上的性能对比.
根据文献[31]本文将训练集中评分数量少于5个的物品所构成的集合称为冷启动物品集.实验1用于比较各种推荐算法在全体物品集和冷启动物品集上的性能,如表3和表4所示.

Table 3 Performance Comparison on All Items表3 全体物品集上的性能对比
Note: The best performing method in each case is boldfaced (lower is better).

Table 4 Performance Comparison on Cold Start Items表4 冷启动物品集上的性能对比
Note: The best performing method in each case is boldfaced (lower is better).
这里需说明的是,针对SVD+与MSRA算法的推荐结果进行成对(pair-wise)的T检验,实验表明所有提升对应的p值都小于0.01,即在传统的矩阵分解模型中融合多源异构信息能够显著提升推荐的性能.从2个表中的实验结果可得出5个结论:
1) 由表3可知,在4个数据集上TrustSVD与SVD++相比,其推荐性能有了不同程度的提升,这说明隐式的社会关系有助于提升传统推荐模型的预测精度,这与文献[32-33]的结论是一致的.
2) 在全体物品集和冷启动物品集上,SVD_SR,SVD_CO 均要优于仅考虑评分信息的SVD++算法,这说明在传统推荐算法基础之上融合额外信息不仅更准确地对用户和物品进行了建模,而且有助于缓解物品的冷启动问题.
3) 在冷启动场景下,考虑物品视觉特征的SVD_V明显优于SVD++,因为SVD_V将物品的视觉特征融入传统推荐算法SVD++可预测目标用户对新物品(即训练集中无评分记录的物品)评分.
4) 相比于SVD_SR和SVD_V仅考虑一种辅助信息,VMCF具有更高的预测精度.这说明综合考虑多源数据(替代关系和视觉信息)有助于更为准确地刻画用户和物品的潜在特征向量.
5) 在4个数据集的冷启动物品集上,SVD_V相比于SVD++的提升幅度分别为0.20%,0.43%,0.74%,1.44%.不难看出融合物品视觉特征的SVD_V算法在Clothing_Shoes_and_Jewelry数据上提升最为明显,这是因为:①该数据集中新物品的数量较多;②用户在购买或对物品评分时,服装、首饰等物品更易受到视觉特征的影响.
实验2.不同评分数量下的性能对比.

Fig. 5 Distribution of items with different ratings图5 不同评分数量下物品的分布
为了对比拥有不同评分的物品上各算法的精度,本文根据训练集中物品所拥有的评分数目把物品分为[1∶5],[6∶10],[11∶20],[21∶40],[41∶100],100以上这6组.由于分组中不包括新物品数量,因此6组物品所占比例之和小于1.图5显示了各数据集中每组物品所占的比例,从图5中可看出各数据集中拥有评分数目少于5个的物品占绝大部分.依据物品拥有的评分数目进行划分之后,使用训练集来学习各对比算法,然后在6组物品上分别计算RMSE.从图6的实验结果中可得出结论:
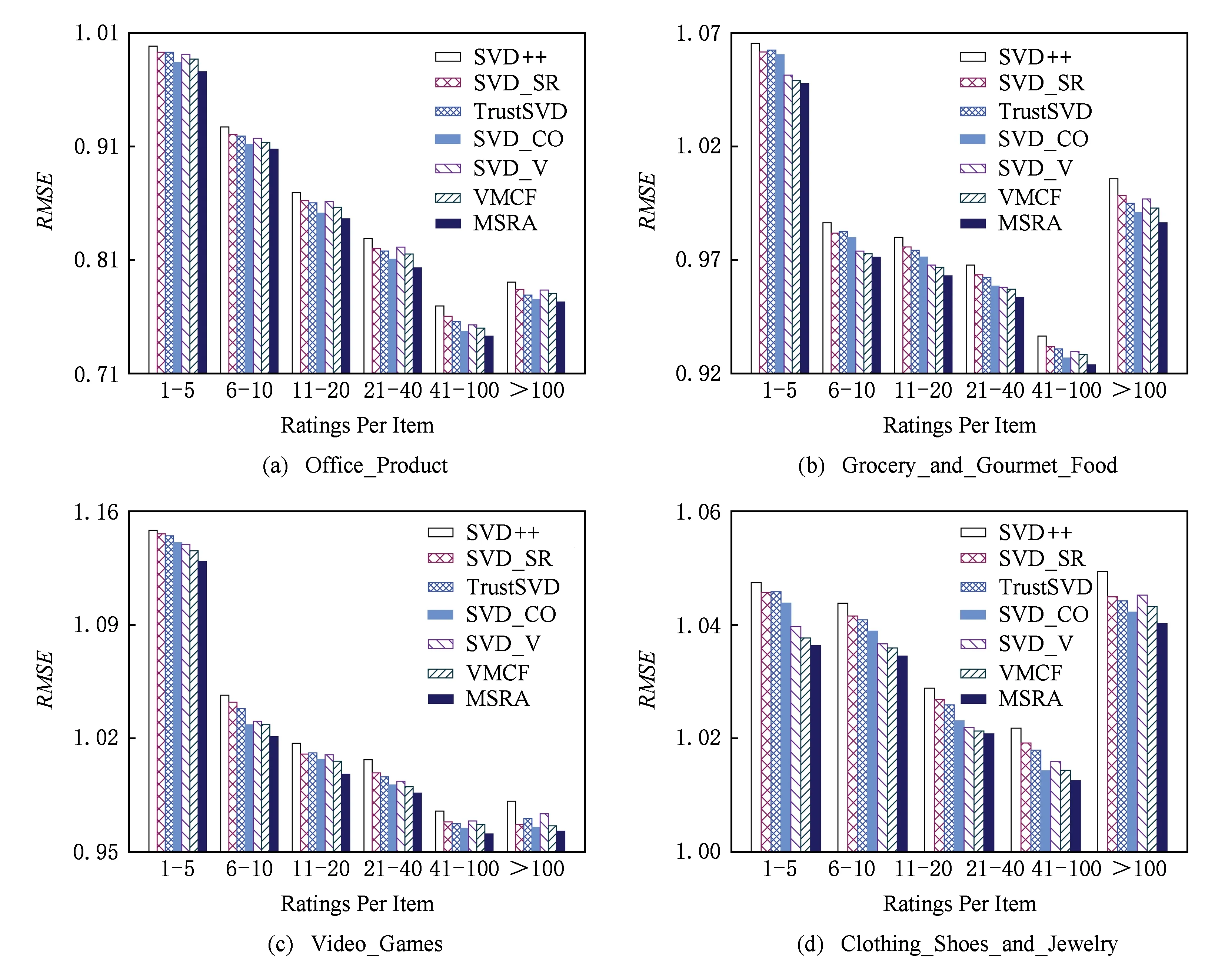
Fig. 6 Comparison on users with different ratings图6 不同评分数量下用户对比结果
1) 在数据较为稀疏时,SVD_SR和SVD_CO算法相比于SVD++提升较少,这是因为拥有评分较少的物品往往刚加入系统或处于长尾数据的尾端,这使得系统可使用的“also_viewed”和“bought_together”信息也较少.但随着物品拥有评分数量的增加,物品趋向流行,其所拥有的关系信息变得更加丰富,因此算法提升幅度增加.
2) 在6组物品上,SVD_V明显优于SVD++,这是说明物品的视觉特征信息不仅可提升物品排序任务的精度[26],而且可提升评分预测任务的性能.
3) 随着物品拥有评分数目的增多,各推荐算法所得出的RMSE值并未持续下降.这因为物品拥有的评分数目较少时,数据比较稀疏使得模型不易学习到用户的潜在特征向量.物品的评分数目增多,物品趋向流行,这使得流行物品对于学习用户的潜在特征向量的贡献度较少.但MSRA仍优于其他对比算法,这因为用户对物品的评分往往受多种因素所致,综合考虑多源异构信息的MSRA算法可更加准确地对用户和物品进行建模.
实验3.超参数对算法的影响.
为了分析超参数对MSRA算法精度的影响,本文以数据集Grocery_and_Gourmet_Food为例详细讨论了各超参数下的实验结果.本文设定超参数λH的取值为0,0.01,0.1,0.3,0.5,1.0,超参数λE的取值为0,1,10,30,50,100.从图7和图8中可得出结论:

Fig. 7 The impact of λH图7 λH的影响
1) 超参数λH控制着物品的互补关系在用户决策时所占的比重,其实验结果如图7所示.λH=0表示不考虑物品之间的互补关系.随着λH的增加,MSRA算法的精度有所提高,这说明考虑物品之间的互补关系有助于提高推荐系统的性能.在λH=0.3以后算法的精度开始下降,这主要是因为λH过大会导致推荐算法过度依懒物品之间的互补关系.
2) 超参数λE用于控制用户对物品的喜好受视觉特征影响.图8显示了超参数λE的变化对RMSE的影响.λE=0时算法的精度最低,这是因为λE=0表示本文的模型在求解参数E时不对其惩罚,导致MSRA算法过拟合,从而使得精度降低.随着λE的增加,其RMSE值出现较小程度的降低(如λE≥30),推荐精度基本趋向平稳,这说明MSRA算法在λE≥30后对该超参数选择不再敏感.
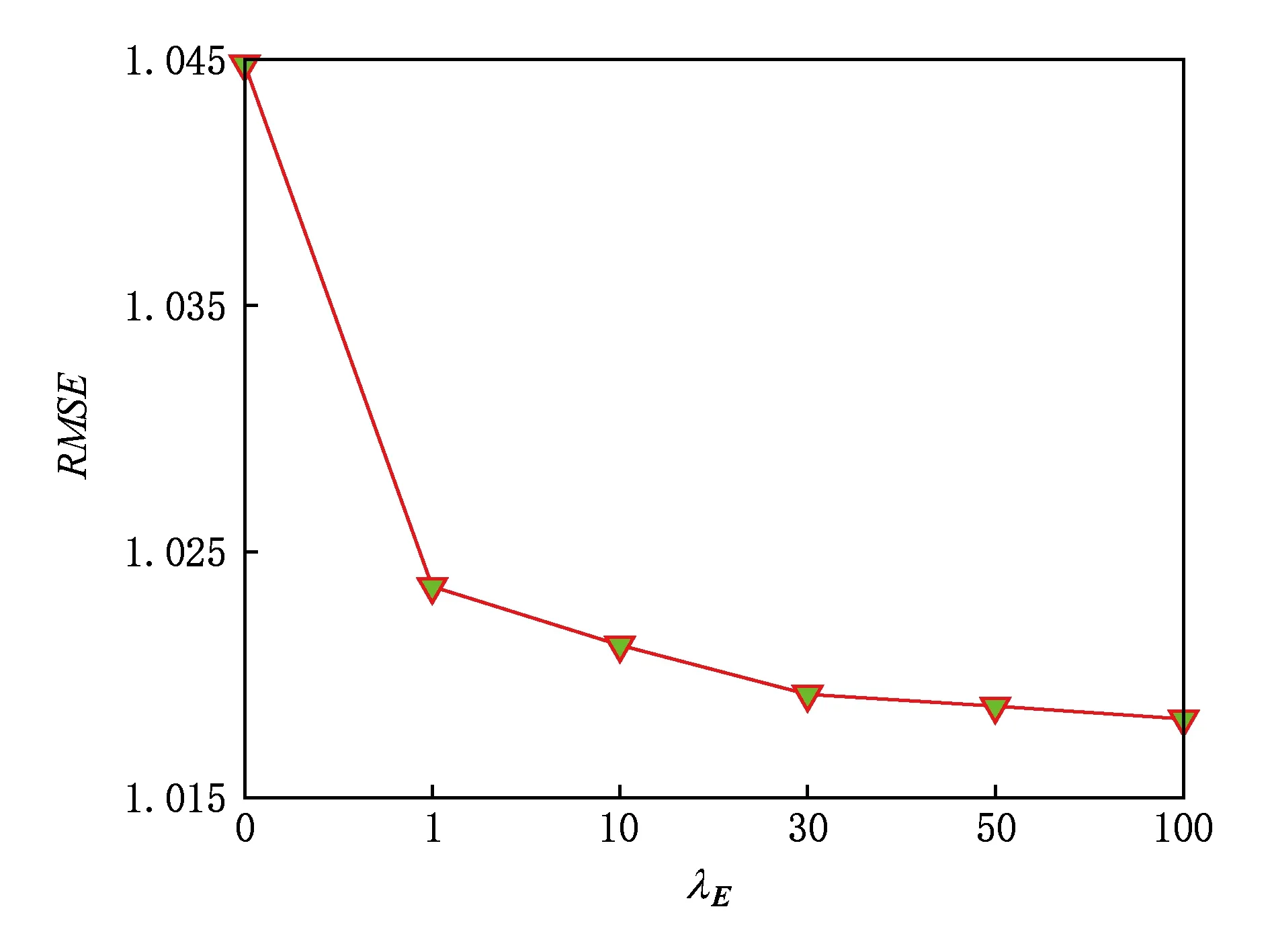
Fig. 8 The impact of λE图8 λE的影响
5 结 论
针对如何将多源异构数据应用到推荐系统中这一亟待解决问题,本文首先定义并分析了不同类型数据的特点,设计了各类型数据融入矩阵分解模型的方式.其后,提出一种面向多源异构数据的矩阵分解推荐模型,较大程度缓解了数据稀疏和物品冷启动问题.本文的模型最大的优势在于将用户的历史喜好信息、社会关系、替代关系、互补关系、物品的视觉特征等多个方面因素融合到统一的框架中,这是一个新颖且具有挑战的工作.在4个数据集上与主流推荐算法进行了详细对比分析,其实验结果表明:本文的MSRA算法不仅可缓解物品的冷启动问题,而且能够准确地预测不同类型物品的实际评分.
在未来的研究中,我们将把重点放在推荐系统的物品排序任务上.这种情况下,如何合理地将多源异构信息用于提升排序相关的推荐模型精度,这是一个值得探索的方向.

