障碍空间中基于Voronoi图的不确定数据聚类算法
万 静 崔美玉 何云斌 李 松
(哈尔滨理工大学计算机科学与技术学院 哈尔滨 150080)
近年来,随着人们对信息技术的不断了解,数据的聚类[1]问题在许多应用中不断出现,如基于传感器网络、基于位置的服务等领域.由于在数据采集过程中,受周围环境的影响,或者是采集仪器精度的限制,因此数据具有不确定性.不确定数据[2-3]的分析与挖掘技术已成为最近几年的研究热点,不确定数据的聚类问题,就是如何将不确定数据集合划分成若干个簇,使最终的结果簇内元组间相似性较大,簇与簇之间元组相似性较小.
现有的聚类算法大多解决的是确定数据的聚类问题,对于不确定数据的聚类算法研究中,主要的研究方法是对传统的面向确定数据的聚类方法进行扩展,即在传统的聚类算法[4-5]如基于划分的聚类、基于密度的聚类、基于网格的聚类以及基于层次和模型的聚类方法等基础上对不确定数据进行建模,使用合适的相似性度量方法,进而提出不确定数据聚类算法.
国内外学者研究了基于划分的不确定聚类算法UK-means[6-7],算法是用最小边界矩形(minimum bounding rectangle, MBR)来表示数据的不确定性,MBR描述了数据点可能出现的区域位置,但UK-means算法只能发现球状簇,并且易受参数k的影响.为了解决大多数聚类划分算法发现簇形状单一的缺陷,Hao等人提出采用基于密度[8]的聚类算法.Kriegel等人根据经典DBSCAN(density-based spatial clustering of applications with noise)算法提出了FDBSCAN(a fast DBSCAN algorithm)[9]算法,Han等人根据OPTICS(ordering points to identify the clustering structure)算法提出了FOPTICS[10]算法,FDBSCAN算法采用距离分布函数作为数据间相似性度量的标准,而FOPTICS算法在处理大型数据集方面更有效.文献[11]提出了FDBSCAN算法的改进算法,多核M-FDBSCAN(multicore-FDBSCAN)方法是通过半聚类发生分裂和合并来构造最终的簇.基于密度的聚类算法大多需要依赖Eps和Minpts这2个参数,陆亿红等人[12]提出了OLUC(optimalk-nearest neighbors and local density-based clustering algorithm for uncertain data)算法,采用动态自适应的最近k近邻结构,计算局部相对密度,降低了参数的选择和密度等级的敏感性.由于网格结构能够提高聚类速度,因此韩利钊等人[13]提出基于区域划分的DBSCAN多密度聚类算法,利用网格相对密度差把数据空间划分成密度不同的区域,使用网格与密度相结合的方法,提高了聚类效率.Kao 等人[14]利用Voronoi图和R树的性质,提出剪枝策略来减少期望距离的计算.以上算法仅考虑了确定元组间的距离,没有考虑元组间的不确定因素和数据间的概率分布,因此采用KL距离作为数据对象间的相似性度量标准.
选址问题在物流、生产生活方面有着广泛的应用,如工厂、垃圾处理中心、物流中心的选址等.随着电商的发展,网上购物的人越来越多,物流发展迅速,物流中心选址的好坏直接影响到服务质量、服务的效率和成本,从而影响到利润和市场竞争力,合适的选址会给人民生活带来便利.由于现实生活中存在一些地理条件的限制(如江河、湖泊、建筑、车辆等),使得聚类分析不可能都在理想的欧氏空间中进行,因此在进行相似性度量时,需要考虑障碍[15]的存在.然而现实生活中的障碍物不可能一直静止不变,空间障碍物往往会发生动态改变,障碍物的改变可能使得原有聚类结果发生改变,因此研究静态障碍空间和动态障碍空间中的不确定数据聚类问题有较大的意义.
近几年来,带有障碍的空间聚类问题受到越来越多国内外研究者的关注,曹科研等人[16]提出了一种障碍空间中的不确定数据聚类算法,分别基于R树、最近距离区域和Voronoi图的性质,设计了高效的剪枝策略,并较高程度地实现了不确定数据的聚类算法.文献[17]提出的带障碍约束空间聚类算法比遗传K-Medoids[18]具有较高的收敛速度.在聚类分析时,考虑障碍的约束,实用价值更高.
在障碍空间中,现有的数据聚类研究成果大多都是针对确定数据的聚类问题.为了解决障碍空间中的不确定数据聚类问题,利用Voronoi图对数据空间进行划分.根据障碍集合是否发生变化,提出了静态障碍环境下的不确定数据聚类算法和动态障碍环境下的不确定数据聚类算法,其中动态障碍物分3种情况处理,分别是障碍物动态增加时的不确定聚类算法DYNOC_VUBSCAN、障碍物动态减少时的不确定聚类算法DYNOR_VUBSCAN和障碍物动态移动情况下的不确定数据聚类算法DYNOM_VUBSCAN.理论研究和实验表明:所提算法具有较高的准确性.
1 定义与性质
定义1.不确定数据点集[19].不确定数据集为X={X1,X2,…,Xn},Xi表示一个不确定数据点.Xi={(x1,p1),(x2,p2),…,(xd,pd)},每个xi表示Xi的属性值,d为维度数.为每一条数据的每一维属性值生成[0,1]区间内的概率值pi,以元组的形式表示,元组由数据值和概率组成.
定义2.障碍集.一个障碍用一个多边形表示,记为Oi,其中障碍的顶点集用V={v1,v2,…,vk}表示,障碍的边集用E={e1,e2,…,ek}表示,记为Oi(V,E).障碍集用O={O1,O2,…,Om}表示.
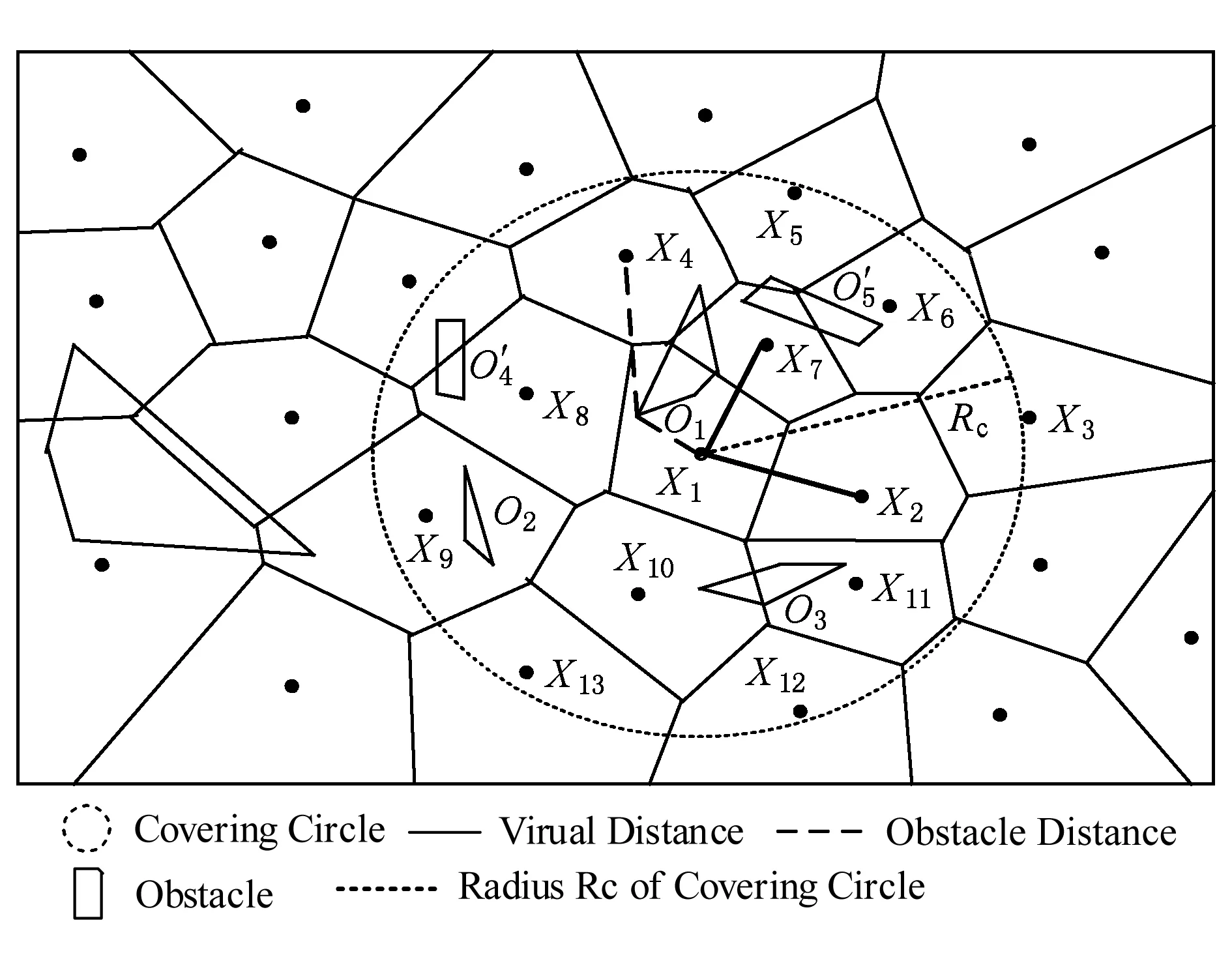
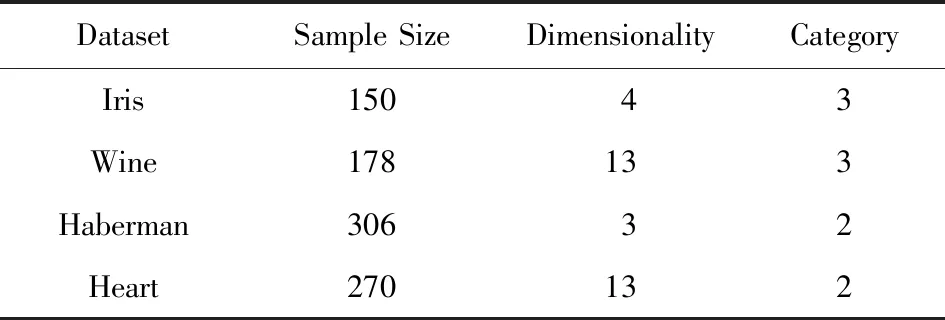
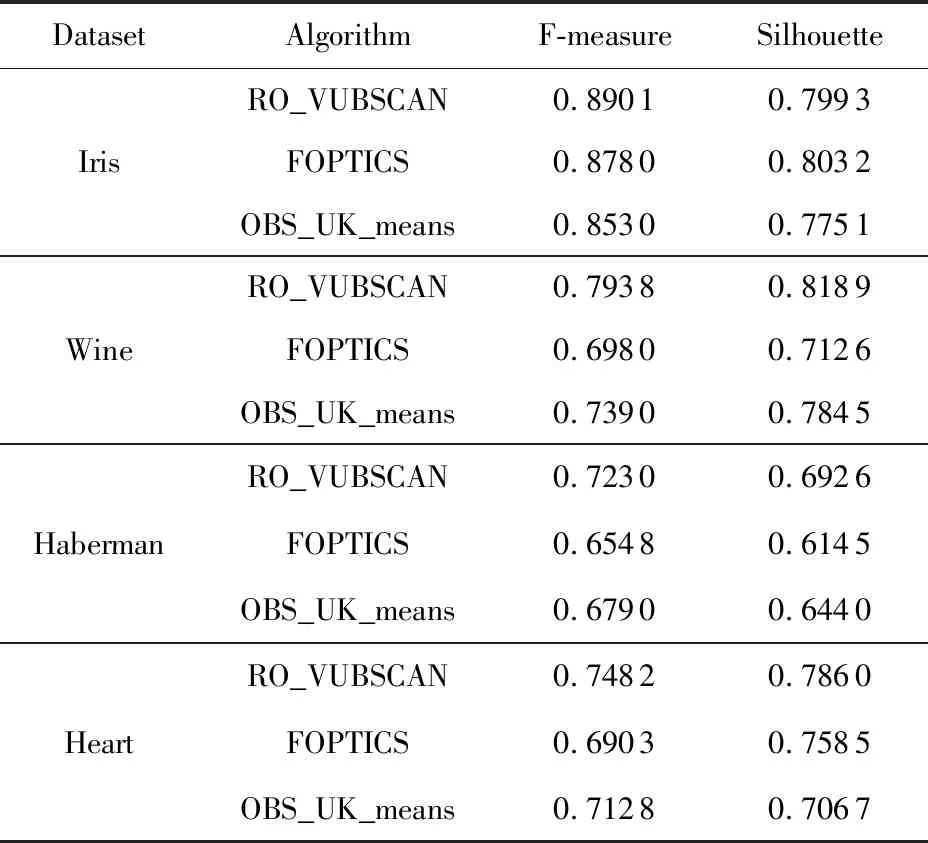
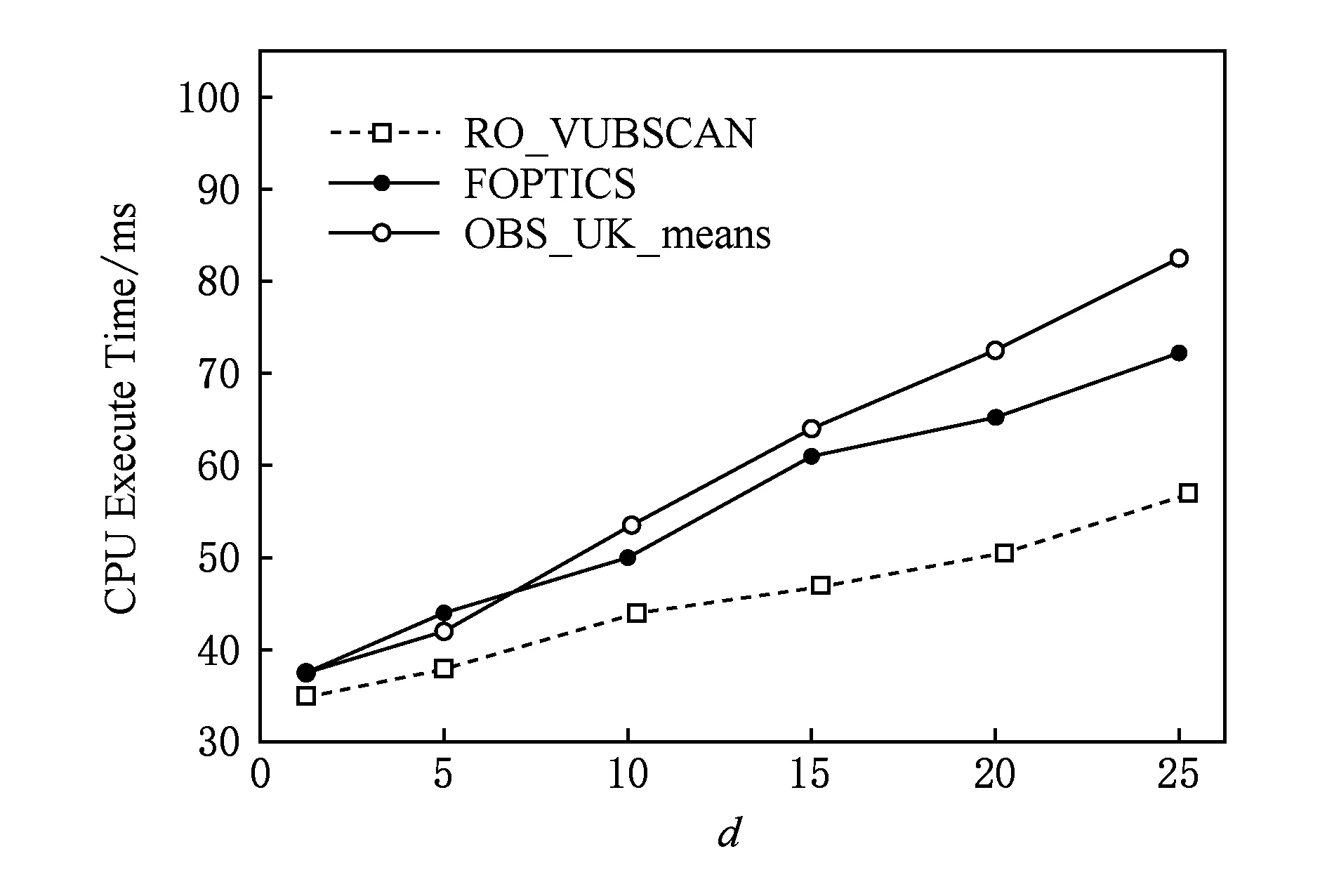
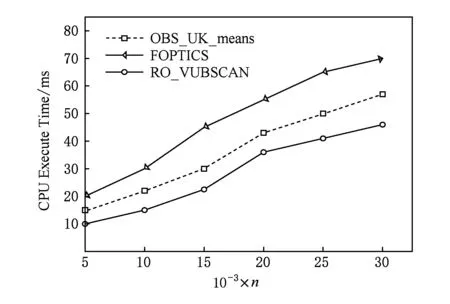
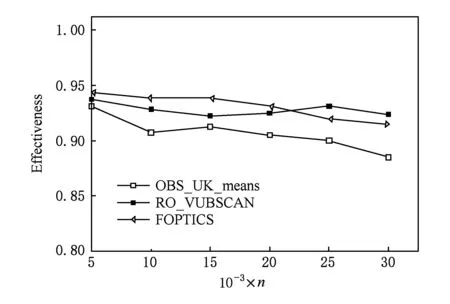
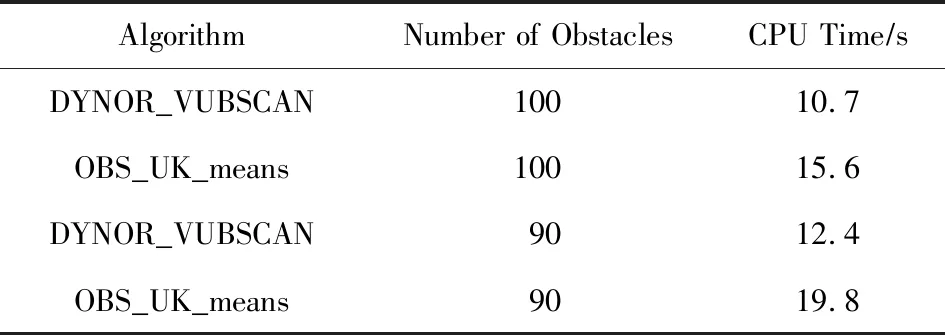
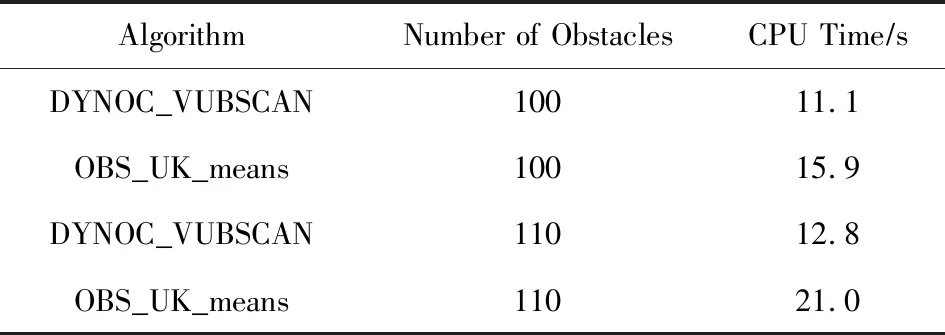
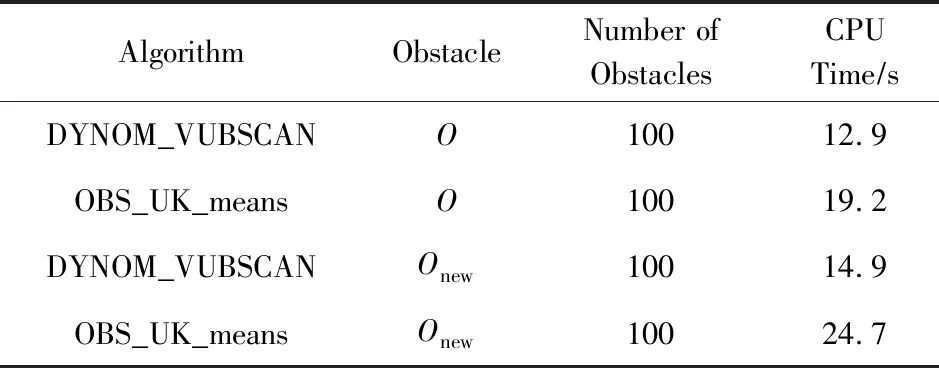
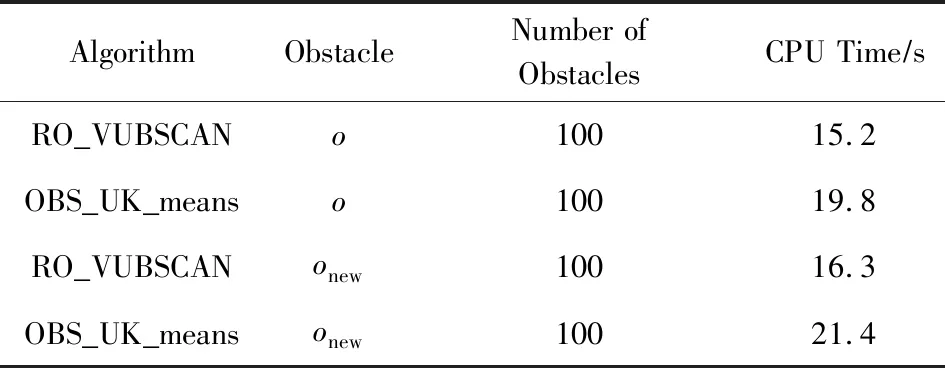
定义3.Voronoi图[20].给定一组生成点X={X1,X2,…,Xn}⊂R2,其中2 定义4.邻接多边形[21].共享相同边的Voronoi多边形称为邻接多边形,它们的生成点被称为邻接生成点.Voronoi单元中存在几条边,则就会有几个邻接多边形.如图1所示,X11的Voronoi单元中有5条边,对应的邻接生成点为X1,X2,X10,X12,X13.X11的邻接多边形为以上5个邻接生成点所在的Voronoi单元. Fig. 1 An example of obstacle distance图1 障碍距离的示例 根据Voronoi图的结构和定义可以得出2个基本性质. 性质1.任意2个多边形不存在公共区域[18].Voronoi图将不确定数据对象集合中的数据按照其最近邻特性将空间进行划分,生成互不重叠的区域. 性质2.临近特性[20].生成点Xi与邻接多边形中的邻接生成点距离最近. 定义5.Voronoi图的k级邻接生成点[20].给定一组生成点X={X1,X2,…,Xn}⊂R2.Xi的k级邻接生成点定义如下: 1) 一级邻接生成.AG1(Xi)={Xj|VX(Xi)和VX(Xj)有公共边}. 2)k(k≥2)级邻接生成点.AGk(Xi)={Xj|VX(X)和VX(Xj)有公共边,X∈AGk-1(Xi)}. 定义6.覆盖圆半径Rc.半径Rc的选取,需要考虑的是整个不确定数据空间,半径Rc过小,覆盖圆内包含的不确定数据点的个数就越少,相应的点的密度就越小,使聚类迭代次数增加.半径Rc过大,容易将孤立点包含在覆盖圆中,因此Rc的确定是重要的. 定义7.KL距离[22].KL距离也叫作相对熵,KL距离衡量的是相同事件空间里的2个概率分布的差异情况,KL距离函数表达式为 (1) 在定义域D中,将不确定对象作为一个服从一定概率分布的随机变量.在连续的定义域中,不确定数据用概率密度函数(probability density function, PDF)[23]表示,概率密度函数用高斯核密度估计: (2) 在离散的情况下,不确定数据用概率质量函数(probability mass function, pmf)表示.根据文献[22],KL距离表达式为 (3) KL距离有2个基本性质: 性质3.非对称性[22].KL距离从直观上是个度量或距离函数,但它并不是一个真正的度量或者距离,因为它不具有对称性,一般从分布P到分布Q的距离通常不一定等于分布Q到分布P的距离.即D(P‖Q)≠D(Q‖P). 性质4.非负性[22].KL距离值非负,即D(P‖Q)≥0.当且仅当2个分布相同时,D(P‖Q)=0. 定义8.聚类半径R[22].聚簇网格内所有不确定数据点与代表点Ci的KL距离的均值,即为不确定聚类半径,其中聚簇网格内所有不确定数据点集合为X={X1,X2,…,Xr}.聚类半径R表达式为 (4) 其中,r表示聚簇内不确定数据点的总个数. 定义9.不确定数据点之间的可视性[16].给定障碍集O和数据点Xi和Xj,不确定数据点Xi和Xj是可视的当且仅当Xi和Xj之间的连线不会穿过障碍集O中任何障碍的内部,也不会与任何边集相交.数据点Xi和Xj是不可视时,Xi和Xj之间的连线会穿过障碍集O的内部或有边集相交.将存在障碍的Voronoi单元标记为阻塞Voronoi单元VX′. 定义10.不确定数据点之间的障碍距离[16].给定障碍集O和数据点Xi和Xj,当Xi与Xj之间互为可视时,Xi与Xj的障碍距离为KL距离,表示为D(Xi‖Xj).当Xi与Xj之间不可视时,Xi与Xj的障碍距离表示为dist(Xi,Xj),数据点之间的障碍距离是绕过障碍的路径最小距离.Xi与Xj之间的障碍距离: dist(Xi,Xj)=min{D(Xi‖vi)+ (5) 图1给出了不确定数据点之间的障碍距离,其中图1中的虚线表示障碍距离,粗实线表示无障碍时的直接距离. 如图1所示,根据式(5)障碍距离的计算,不确定数据点X15与X16之间的障碍距离为 dist(X15,X16)=min{D(X15‖v1)+D(v1‖X16), 定义11.不确定数据点的密度[24].空间中的任意一个不确定数据点Xi,1≤i≤n.以不确定数据点Xi为中心,Rc为半径的覆盖圆区域内的不确定数据生成点个数,称为不确定数据点的密度,记作ρ(Xi). 定义12.核心对象.根据给定阈值ε,最大覆盖圆半径Rc,若不确定数据对象Xi的最大覆盖圆中包含的不确定数据对象个数ρ≥ε时,则称Xi为核心对象. 随着数据规模越来越大,使用基于密度的聚类算法能发现任意形状的聚簇,并且对孤立点数据不敏感.使用Voronoi图将数据空间划分成若干个空间单元,根据Voronoi图的邻接特性和所提出的规则对不确定数据进行聚类,使最终的聚类结果有较高的执行效率和准确性. 静态障碍环境指的是空间障碍物集合不会发生改变,包括障碍的位置、障碍的点集和边集都不发生变化.对此时的空间不确定数据实现聚类算法,并提出了STAO_VUBSCAN算法. STAO_VUBSCAN算法的主要思想:在一定距离内,可根据Voronoi单元与其邻接的Voronoi的级数大小,判定局部密度大小.找出核心对象,以不确定数据点Xi为中心,以Rc为半径形成一个覆盖圆,计算覆盖圆内所含的不确定数据点的个数ρ.若ρ>ε,则说明不确定数据点的数量较多,表示Xi所在覆盖圆内的局部密度越大.根据局部密度的中心进而判断邻接Voronoi单元的聚类情况,最终实现静态障碍环境下的不确定数据聚类. 定理1.若不确定数据点Xi在Voronoi图中的所有一级邻接生成点都被当作孤立点,则此时的不确定数据点Xi也同样的视为孤立点. 证明. 设Xj为Xi的所有一级邻接生成点,1≤j≤6[20].若Xj为孤立点,说明所有Xj所在覆盖圆的数据密度都较小,不能视为核心对象.则以Xi为中心,Rc为半径的覆盖圆内的数据密度也较小.由于Xj为孤立点被剪枝,此时所有Xj的中心Xi也必定被视为孤立点处理. 图2中,不确定数据点X1为圆心的覆盖圆中,覆盖圆内的X1最大有2级生成点,所以在进行相似性度量时,只考虑2级生成点以内的不确定数据和障碍情况,2级以外的邻接生成点和障碍物可先不作考虑,这会简化KL距离的计算以及障碍的判断.判断每个核心对象所在的覆盖圆内数据点聚类情况,使得聚类过程更加简便有效. Fig. 2 An example based on Theorem 1图2 基于定理1的示例 算法STAO_VUBSCAN的主要步骤:首先选择任一未划分的不确定数据对象,根据不确定数据点密度大小,先对密度大的生成点设置为核心对象.将核心对象根据密度从大到小降序排序,存放在Hash表L中,L={X1,X2,…,Xt},1≤i≤t.根据核心对象在Hash表中的顺序来依次聚类,将判断过的不确定数据从Hash表中删除,直到Hash表为空为止.使用KL距离作为相似性度量标准,寻找所有可能被聚到此类的不确定数据点,并将这些数据点标记为一类,并根据定理1进行部分孤立点的处理.重复以上步骤,直到所有不确定数据对象划分完毕. 基于以上讨论,进一步提出静态障碍环境下的不确定数据聚类算法STAO_VUBSCAN,如算法1所示. 算法1.STAO_VUBSCAN(X,O,ε,Rc). 输入:不确定数据点集X、障碍集合O、覆盖圆半径Rc,ε,R; 输出:障碍空间下的不确定数据聚类结果W. ① fori=1 tondo ②Calculate_den(Xi); ③ end for ④ ifρ≥ε ⑤L←Quick_Sort(Xi);*降序排序* ⑥ end if ⑦ for (i=1 tot)且L≠∅ do ⑧ ifXi与Xj可视 ⑨Calculate_KL();*式(2)或式(3)* ⑩ ifD(Xi‖Xj)≤R 首先算法1在创建Voronoi时,构建所需的时间复杂度为O(nlgn).算法执行第1个for循环,遍历不确定数据点所需的时间复杂度是O(n).由于n的个数是有限的,所以此步骤是可终止的.在对核心对象进行快速排序时所需的时间复杂度为(mlgm),其中m表示的是核心对象的个数,m≪n.算法执行第2个for循环所需的时间复杂度为O(t),因为覆盖圆内核心对象t的数量有限,所以此步骤也是可终止的.由以上算法的核心步骤的时间复杂度分析可知,算法总的时间复杂度为O(nlgn).算法1的计算代价主要受空间数据集的规模、计算无障碍情况下距离度量的计算量和存在障碍时的障碍距离计算量的影响. 算法1已经解决了静态障碍空间中的不确定数据聚类问题.但是算法1只考虑覆盖圆内不确定数据点密度,根据覆盖圆内不确定数据点密度大小,定义核心对象,而没有考虑到核心对象所在覆盖圆内的障碍的多少.针对覆盖圆内静态障碍物的分布情况,进一步提出STAO_RVUBSCAN算法,算法利用Voronoi图的邻接特性和提出的规则,设计了高效的聚类方法. 规则1.如果最大覆盖圆内不确定数据点密度较大,并且满足ρ≥ε,但存在的障碍较多时,则对应的不可视集合S2中的不确定数据点就会较多,在进行相似性度量时,计算的是障碍距离.若dist(Xi,Xj)>R,则Xi所在覆盖圆内的不确定数据点Xj不能加入到Xi所在的簇中. 只考虑核心对象的密度是不够的,还需要考虑核心对象最大覆盖圆内静态障碍的密度,障碍密度越大,说明不可视集合S2内的不确定数据个数就越多,判断集合S1中可视数据密度是否满足ρ≥ε.如果满足,执行过程跟算法1一致.否则,说明了核心对象周围的障碍较多,不可视集合S2内的不确定个数较多.在进行相似性度量时计算的是障碍距离,因为每个障碍距离都大于没有障碍时的可视距离,因此需要考虑核心对象是否被当作孤立点处理. 如图3所示,以不确定数据点X1为圆心,Rc为半径的最大覆盖圆内不确定数据集合S为{X1,X2,X4,X5,X6,X7,X8,X9,X10,X11,X12,X13},此时不确定数据点密度较大.覆盖圆内存在O1,O2,O3,O4,O5共5个障碍,障碍将不确定数据分为2个集合,分别为可视集合S1和不可视集合S2.根据分析得出,可视集合S1={X7,X8,X10,X13},不可视集合S2={X2,X4,X5,X6,X9,X11,X12}. Fig. 3 An example based on regulation 1图3 基于规则1的示例 若S1中不确定数据密度远小于ε,或者S2中不确定数据密度≥ε,说明覆盖圆内不确定数据点Xi的周围存在较多的障碍,此时Xi不能作为核心对象处理.连续域环境下,可视集合内的距离使用式(2).离散域环境下,可视集合内的距离公式使用式(3),不可视集合内的障碍距离用式(5)度量.规则1的提出,减少了障碍距离的判断,使得算法的效率较大程度地提高. 首先判断核心对象所在覆盖圆内障碍的情况,如果核心对象内的静态障碍不影响聚类结果,则聚类结果跟算法1相同.如果核心对象所在覆盖圆内障碍的密度较大,只需判断不可视集合S2中数据的聚类情况.最后根据相似性度量标准,将覆盖圆内的不确定数据划分到合适的聚簇中.基于以上分析,进一步提出了静态障碍环境下的不确定数据聚类精炼算法STAO_RVUBSCAN,如算法2所示. 算法2.STAO_RVUBSCAN(X,O,ε,Rc,L). 输入:X,O,Rc,ε,R,L; 输出:聚类结果W. ① for (i=1 tot)且L≠∅ do*规则1* ②S←Count_ρ(Xi); ③ ifCircle_R(Xi)∃Oi*覆盖圆中存在障碍时* ④S1←Visiable_X(Xi,Xj);*1≤j≤S* ⑤S2←NVisiable_X(Xi,Xj); ⑥ end if ⑦ ifCount_S1≥ε ⑧Calculate_KL();*式(2)或式(3)* ⑨ ifD(Xi‖Xj)≤R ⑩W←Xi,Xj; 算法2在创建Voronoi时,构建所需的时间复杂度为O(nlgn).算法执行只有一个for循环,所需的时间复杂度为O(t),因为覆盖圆内核心对象t的数量有限,所以此步骤也是可终止的.由以上时间复杂度分析可知,算法2总的时间复杂度为O(nlgn). 算法2的聚类效率优于算法1,由于规则1的提出,过滤了大量的不确定数据点的判断,减少了大量的计算,也使得最终的聚类结果更准确. 算法1和算法2研究的是静态障碍物环境下的不确定数据聚类算法,但是现实生活中的空间障碍物往往会发生动态改变,如空间障碍物的位置发生改变,障碍物的点集和边集发生改变,因此提出动态障碍情况下的不确定数据聚类算法.根据障碍物动态变化的不同情况,分别提出障碍物动态增加、障碍物动态减少和障碍物动态移动3种情况的不确定数据的聚类算法. Fig. 4 An example of dynamic increase in obstacles图4 障碍动态增加的示例 根据新增加的障碍物的位置分析,障碍物增加对聚类可能没有影响,也可能有影响. 规则2.首先判断新增加障碍的位置,然后计算障碍所在Voronoi图中不确定数据点的最大覆盖圆范围.如果新增加的障碍对聚类结果无影响,覆盖圆范围内不影响聚类的结果,则聚类结果与算法2 的结果相同.若新增障碍对不确定结果有影响,覆盖圆范围内的新增障碍影响了Voronoi图中不确定数据点的聚类,则对此覆盖圆内的不确定数据点重新聚类.重新聚类可能引起其他类的聚类,因此根据Voronoi图的邻接特性,需将可视性改变的不确定数据点加入到离其最近的邻接核心对象所在的聚簇中. 由以上分析可知,障碍物的增加对不确定数据聚类的影响是局部的,分情况判定处理会避免较多不必要的距离计算,因此提出规则2对动态增加的障碍进行具体分析,进一步提出了障碍物动态增加时的不确定数据聚类算法DYNOC_VUBSCAN,如算法3所示. 算法3.DYNOC_VUBSCAN(X,O,ε,Rc). 输出:聚类结果W. ② fori=1 tondo ④Calculate_R(Xi); ⑦W←STAO_RVUBSCAN();*调用算法2* ⑩ ifdist(Xi,Xj)≤R 首先算法3在创建Voronoi时,构建所需的时间复杂度为O(nlgn).算法3只有一个for循环,遍历不确定数据点所需的时间复杂度是O(n).n代表的是不确定数据的总数量,并且数量是有限的,所以算法是可终止的.当算法3满足步骤⑥所需的条件时,调用算法2.算法2的时间复杂度已经分析得出是O(nlgn).由以上分析可知,算法3总的时间复杂度为O(nlgn). 数据空间的障碍物可根据实际情况动态变化,当障碍物减少时也很有可能对原来的聚类结果产生影响. 规则3.当减少障碍物时,没有改变最后的聚类结果,此情况的聚类结果跟静态障碍环境下的不确定聚类算法结果相同,使用算法2完成聚类即可.当减少的障碍物能够引发最终的聚类结果改变,则对减少的障碍所在的Voronoi单元的最大覆盖圆内的不确定数据重新进行相似性度量计算.重新聚类可能引起其他类的聚类,因此根据Voronoi图的邻接特性,需将不可视变成可视时集合中的不确定数据点加入到离其最近的邻接核心对象所在的聚簇中. Fig. 5 An example of dynamic reduction in obstacles图5 障碍动态减少的示例 根据减少的障碍物的具体位置,减少的障碍可能对聚类影响,也可能对聚类结果没有影响,因此需要分析讨论.算法的主要思想:首先得到新的障碍集合Onew,判断减少的障碍物的位置.然后根据规则3分析减少的障碍对聚类是否有影响,最后得到障碍动态减少情况下的不确定数据聚类结果. 基于以上讨论,具体地给出动态障碍减少情况下的不确定数据聚类算法DYNOR_VUBSCAN,如算法4所示. 算法4.DYNOR_VUBSCAN(X,O,ε,Rc). 输出:聚类结果W. ② fori=1 tondo ④Calculate_R(Xi); ⑦q←Count_S′(); ⑧ ifS′=∅或q=0 ⑨W←STAO_RVUBSCAN();*调用算法2* ⑩ else ifS′≠ ∅ 首先算法4在创建Voronoi时,构建所需的时间复杂度为O(nlgn).算法执行最外层的for循环,遍历不确定数据点所需的时间复杂度是O(qn).n代表的是不确定数据的总数量,并且数量是有限的,q是障碍减少时,由不可视变成可视的数据点个数,数量也是有限的,所以算法是可终止的.当算法4满足步骤⑧所需的条件时,调用算法2.算法2的时间复杂度已经分析得出是O(nlgn).由以上分析可知,算法4总的时间复杂度为O(nlgn). 由于算法根据障碍将数据划分成可视集合与不可视集合,只需重新判断障碍减少时,由不可视变成可视的不确定数据点聚类情况.此方法大大减少了计算量,使得局部的进行相似性度量比重新划分聚类更有效. 本节研究的是障碍物动态移动情况下的不确定数据聚类,其中障碍物的动态移动指的是障碍物的点集和边集不发生改变,只是障碍物的位置发生改变. 规则4.障碍物的动态移动可以分解成障碍物动态减少和障碍物动态增加2部分,障碍物动态移动之前标记为Oi beg,障碍物移动之后标记为Oi end.假设障碍物由位置P动态移动到位置Q,在位置P时,相当于障碍物Oi beg动态减少,因此需要分析障碍物动态减少时,由不可视集合移动到可视集合中的不确定数据点的聚类情况.在位置Q时,相当于障碍物Oi end的动态增加,因此需要分析障碍物动态增加时,由可视集合移动到不可视集合的不确定数据点的聚类情况. 如图6所示,虚线箭头表示的是障碍物动态移动前后位置的变化情况,根据障碍物动态移动的前后位置,移动后的障碍可能对聚类结果有影响,也可能对聚类结果没有影响,因此可以分为4种情况分析讨论: 1) 障碍物Oi由覆盖圆内部移动到覆盖圆内部,如图6障碍物O3移动到O2的情况. 2) 障碍物Oi在核心对象Xi所在的覆盖圆内部移动到覆盖圆外部,如图6障碍物O3移动到O4的情况. 3) 障碍物Oi在核心对象Xi所在的覆盖圆外部移动到覆盖圆内部,如图6障碍物O1移动到O3的情况. 4) 障碍物Oi在覆盖圆外移动,如图6障碍O1移动到O4的情况. Fig. 6 An example of dynamic movement of obstacles图6 障碍物动态移动的示例 由于覆盖圆的圆心都为核心对象,因此不确定数据的分布是密集的.情况1中的障碍Oi在覆盖圆内移动,动态移动后的障碍集为Onew=O-Oi beg+Oi end;情况2中的障碍Oi由覆盖圆内移动到覆盖圆外,表明障碍Oi end所在区域的不确定数据较稀疏,障碍移动后的位置不影响核心对象的聚类结果,因此Onew=O-Oi beg;情况3中的障碍Oi由覆盖圆外移动到覆盖圆内,表明障碍Oi end所在区域的不确定数据分布是密集的,障碍Oi end移动后的位置会影响核心对象的聚类结果,所以Onew=O-Oi beg+Oi end;情况4中的障碍Oi在覆盖圆外移动,表明障碍Oi beg和障碍Oi end所在区域的不确定数据分布是稀疏的,障碍动态移动之后的位置不影响核心对象的聚类结果,因此Onew=O-Oi beg. 首先标记动态移动的障碍物在移动之前的位置和移动之后的位置,并判断符合以上哪种情况,进而得到Onew.根据规则4,通过调用DYNOR_VUBSCAN算法和DYNOC_VUBSCAN算法,最终实现对动态障碍物移动时的不确定数据进行聚类. 基于以上的分析,给出障碍物动态移动情况下的不确定数据聚类DYNOM_VUBSCAN算法,如算法5所示. 算法5.DYNOM_VUBSCAN(X,O,Oi). 输入:不确定数据集X、障碍集O、移动障碍Oi; 输出:聚类结果W. ①Judge_O(Oi beg,Oi end); ② ifOi beg,Oi endinCircle_R() ③Onew←O-Oi beg+Oi end; ④W1←DYNOR_VUBSCAN(); ⑤W2←DYNOC_VUBSCAN(); ⑥W←W1∪W2; ⑦ end if ⑧ ifOi endinCircle_R()且Oi begnot in Circle_R() ⑨Onew←O-Oi beg+Oi end; ⑩W←DYNOC_VUBSCAN(); Circle_R() 算法5主要通过调用算法2、算法3和算法4来实现,由于以上算法是可终止的,并且时间复杂度已经分析得出为O(nlgn),进而得出算法5的时间复杂度为O(nlgn). 通过分析定义域的情况,分别根据离散区域或者连续域对不确定数据进行聚类,离散域下的不确定数据用概率质量函数表示,连续域下的不确定数据用概率密度函数表示.采用核密度估计[20]方法得出概率密度函数,该方法不需要输入参数,它仅从数据本身对概率密度函数作出估计,并且可以估计任意形状的密度函数.由于概率质量函数在进行相似性度量计算时,比使用概率密度函数更简单,所以对数据域的情况分开处理是有意义的.对于障碍情况的判断,可以根据障碍集合是否变化,判断障碍物是静态的还是动态变化的,最终提出总算法. 根据前面提出的静态障碍物环境下和动态障碍物环境下的不确定数据聚类算法,本节提出RO_VUBSCAN算法,使得最终的算法可以高效地解决静态障碍空间环境下的不确定聚类、动态障碍物增加、减少和移动情况下的不确定聚类问题. 首先判断障碍集合是否变化,如果障碍集合不发生改变,说明解决的是静态障碍环境下的不确定数据聚类问题,可调用算法2完成聚类.若障碍集合发生变化,可根据障碍数量变化判断是障碍物动态增加、障碍物动态减少还是障碍物动态移动的,如果是障碍动态增加时,则调用算法3完成聚类.如果是障碍动态减少时,则调用算法4完成聚类.如果是障碍动态移动时,则调用算法5完成聚类.基于以上分析,进一步提出障碍空间下的不确定聚类算法RO_VUBSCAN,如算法6所示. 算法6.RO_VUBSCAN(X,O,ε,Rc). 输入:不确定数据集X、障碍集O,ε,Rc; 输出:障碍空间下的不确定数据聚类结果集W. ①Create_Vor(X); ②Add_O(O); ③ fori=1 tondo ④Calculate_den(Xi);*计算ρ(Xi)* ⑤Judge_O(O); ⑥ ifO=Onew ⑦W←STAO_RVUBSCAN(); ⑧ else ifO≠Onew ⑨ ifCount_O 如果定义域是连续的,则不确定数据用概率密度函数表示,KL距离的计算使用式(2),如果定义域是离散的,则不确定数据用概率质量函数表示,相似性度量计算使用式(3).在计算障碍距离时,则使用式(5)进行相似性度量. 算法6在创建Voronoi图所需的时间复杂度为O(nlgn).算法执行for循环时,遍历不确定数据点所需的时间复杂度是O(n).n代表的是不确定数据的总数量,并且数量是有限的,所以算法是可终止的.当算法满足步骤⑥所需的条件时,调用算法2.算法2的时间复杂度已经分析得出是O(nlgn).当算法满足步骤⑧所需的条件时,调用算法3、算法4或者算法5,以上算法的时间复杂度都为O(nlgn).由以上分析可得出,算法6总的时间复杂度为O(nlgn). 本节主要通过实验对所提出的算法进行性能分析与比较.根据已有的研究成果发现,在相似性度量方面,大多集中在几何距离的度量上,没有考虑数据间的概率分布.针对这些问题提出了STAO_RVUBSCAN,DYNOC_VUBSCAN,DYNOR_VUBSCAN,DYNOM_VUBSCAN等算法.由于现有的研究成果无法直接有效地处理动态障碍空间中的不确定数据的聚类问题,因此对文献[16]中提出的OBS_UK_means算法中动态添加障碍和动态减少障碍,进而分别与所提算法DYNOC_VUBSCAN,DYNOR_VUBSCAN,DYNOM_VUBSCAN进行实验比较与分析. 根据障碍情况,需要对OBS_UK_means算法做4种处理: 1) 障碍集O=Onew时,则与所提的静态障碍物环境下的聚类情况相同,可利用OBS_UK_means算法与STAO_RVUBSCAN算法做实验对比. 2) 障碍集O≠Onew,并且Count_O 3) 障碍集O≠Onew,并且Count_O>Count_Onew时,表示障碍动态减少,则对障碍集为Onew时的空间中所有不确定数据点重新聚类.将这种障碍动态减少时调用OBS_UK_means的算法与提出的DYNOR_ VUBSCA的方法做实验对比. 4) 障碍集O≠Onew,并且Count_O=Count_Onew时,表示障碍物动态移动.对障碍集为Onew时的所有不确定数据点重新聚类,将这种障碍动态移动时调用OBS_UK_means的算法与提出的DYNOM_ VUBSCA的方法做实验对比. 实验环境:Windows7的64位操作系统,采用Java编程.实验中计算机的硬件配置:8 GB内存,500 GB硬盘,处理器:Intel®CoreTMi3处理器(主频为2.30 GHz). 实验使用标准的UCI实验室数据集[25],详细情况如表1所示: Table 1 UCI Laboratory Datasets表1 UCI实验室数据集 UCI实验室数据集中的数据表示的是确定的数据,为便于实验,在实验过程中对实验数据集进行了适当调整,生成不确定数据的过程具体有5个步骤:1)读取原始数据集的属性;2)遍历数据集的每条数据的每个属性;3)为每一条数据的每一维的属性值随机生成一个概率值,概率值在[0,1]范围之内,最终表达的形式为:Xi={(x1,p1),(x2,p2),…,(xd,pd)},其中每个xi表示Xi的属性值,d为维度,Xi表示一个不确定数据点;4)得到每条数据概率属性值;5)输出不确定数据集. 实验主要考虑6个方面因素:数据维度d、数据基数n、障碍物数量、障碍物分布、CPU运行时间、聚类质量.利用以上6方面作为衡量算法的指标. 常用的聚类有效性评测有内部评价法、外部评价法和相关性测试评价.它们能对聚类结果进行评价,得出聚类结果是否最优.实验采用评测指标(silhouette)作为聚类内部有效性评测,实验采用F-measure熵[26]作为聚类外部评测标准. 分别对各个算法进行50次独立聚类实验,统计每次实验的结果,然后对每种算法求50次实验结果的平均值,对比算法的实验结果如表2所示.结果显示,对于以上4组数据集,RO_VUBSCAN算法的F-measure指标平均值和S指标均值均高于OBS_UK_means算法和FOPTICS算法的评测指标.通过实验可看出,RO_VUBSCAN算法表现出更好的聚类效果. Table 2 Comparison of Effectiveness of Algorithms表2 算法评测有效性对比 图7中OBS_UK_means,RO_VUBSCAN,FOPTICS这3个算法的CPU执行时间随着维度d的增加而增加,其中RO_VUBSCAN算法的CPU执行时间上升趋势较平缓.从实验结果看出,使用KL距离相似性度量方法比其他的距离度量更高效.由于考虑障碍的存在,随着维度的增加,OBS_UK_means算法需要考虑障碍的存在,因此CPU执行时间大于FOPTICS算法. Fig. 7 The effect of dimension d for CPU execution time图7 维度d对CPU执行时间的影响 如图8所示,随着维度d的不断增加,算法的有效性的变化曲线也呈下降趋势.通过实验,得出在维度大于10之后的曲线,算法的有效性变化曲线下降明显,但STAO_RVUBSCAN算法的有效性依然较高.由于DYNOR_VUBSCAN算法和DYNOR_VUBSCAN算法处理的是动态障碍的情况,因此有效性较静态障碍空间下STAO_RVUBSCAN算法的有效性略低一些. Fig. 8 The effect of dimension d on algorithmeffectiveness图8 维度d对算法有效性的影响 图9给出了3个算法的CPU执行时间随着不确定数据样本数变化的对比结果.随着不确定数据样本数的不断增大,FOPTICS算法在数据量增大时,CPU的执行时间急剧上升.但在数据量较小的时刻,因为FOPTICS算法没有障碍的约束,FOPTICS算法的CPU执行时间比RO_VUBSCAN算法的执行时间少.在相同不确定数据样本数的情况下,RO_VUBSCAN的CPU执行时间一直小于OBS_UK_means算法,因此通过实验得知RO_VUBSCAN算法更有效. Fig. 9 The effect of sample number on CPUexecution time图9 样本数对CPU执行时间的影响 图10给出了数据量从5 000增加到30 000的过程中,3个算法对应的CPU执行时间的变化情况.通过实验得出,RO_VUBSCAN算法的CPU执行时间相对于OBS_UK_means,FOPTICS更少.因此得出算法RO_VUBSCAN算法更有效. Fig. 10 The effect of data size on CPU execution time图10 数据量对CPU执行时间的影响 如图11所示,分析了数据量从5 000增加到30 000期间,随着数据量的增加,3个聚类算法的有效性.通过实验结果可看出,FOPTICS算法的曲线平稳,并且效率一直较高.相比于RO_VUBSCAN算法,由于障碍的存在,聚类的过程中,存在着一定的误差,在数据量增加到20 000期间有效性比FOPTICS略低,随着数据量的继续增加,算法的有效性比FOPTICS高.相比于OBS_UK_means算法,RO_VUBSCAN算法更有效. Fig. 11 The effect of data size on the effectivenessof algorithm图11 数据量对算法有效性的影响 表3给出了障碍物动态减少时DYNOR_VUBSCAN算法与对比算法的CPU执行时间的比较情况.结果显示,DYNOR_VUBSCAN算法的CPU执行时间均小于对比算法,当障碍物动态减少时,由于对比算法需要计算全部数据,因此CPU执行时间远大于DYNOR_VUBSCAN算法. Table 3 The Effect of the Dynamic Reduction of Obstacles on the Execution Time of CPU表3 障碍物动态减少对CPU执行时间的影响 表4给出了障碍物动态增加时DYNOC_VUBSCAN算法与对比算法的CPU执行时间的比较情况,在障碍物数量动态增加时,DYNOC_VUBSCAN算法的CPU执行时间变化不大,而对比算法的CPU执行时间变化则较大.结果表明:所提算法优于对比算法. Table 4 The Effect of the Dynamic Increase of Obstacles on the Execution Time of CPU表4 障碍物动态增加对CPU执行时间的影响 表5给出了障碍物动态移动时DYNOM_VUBSCAN算法与对比算法的CPU执行时间的比较情况.结果显示DYNOM_VUBSCAN算法的CPU执行时间远小于对比算法的CPU执行时间. Table 5 The Effect of the Dynamic Movement of Obstacles on the Execution Time of CPU表5 障碍物动态移动对CPU执行时间的影响 表6显示了障碍物数量增加时STAO_RVUBSCAN算法与对比算法的CPU执行时间的比较情况,在障碍物数量不断增加时,STAO_RVUBSCAN算法的CPU执行时间增加的趋势较缓慢,而对比算法的CPU执行时间变化较大. 表7给出了障碍物分布不同时RO_VUBSCAN算法与对比算法的CPU执行时间比较情况,障碍物的分布是随机的,结果显示RO_VUBSCAN算法的CPU执行时间变化不大,并且执行时间均小于对比算法. Table 6 The Effect of the Different Number of Obstacles on the Execution Time of CPU表6 不同数量的障碍物对CPU执行时间的影响 Table 7 The Effect of Different Location Distribution of Obstacles on the Execution Time of CPU表7 障碍物不同位置分布对CPU执行时间的影响 通过以上实验分析可知,提出的静态障碍物环境下的不确定数据聚类算法STAO_RVUBSCAN与动态障碍物环境下的DYNOC_VUBSCAN,DYNOR_VUBSCAN,DYNOM_VUBSCAN不确定聚类算法均具有较高的效率. 传统的聚类算法大多是在欧氏空间进行,没有考虑障碍的存在.由于现实生活中,不确定数据点之间可能存在障碍,因此本文根据障碍物集合是否发生变化,把障碍大致分成2种情况,分别对静态障碍空间下和动态障碍空间下的不确定数据进行聚类分析.静态障碍空间中,提出了STAO_VUBSCAN算法和精炼算法STAO_RVUBSCAN.精炼算法的提出,使得聚类结果更准确和高效.对于动态障碍,考虑了障碍物动态增加、障碍物动态减少和障碍物动态移动3种情况,分别对这3种情况进行分析,提出了DYNOC_VUBSCAN算法、DYNOR_VUBSCAN算法和DYNOM_VUBSCAN算法.理论研究和实验分析验证表明,提出的算法具有较高的性能.由于没有对确定数据进行聚类分析,未来研究的重点主要是障碍物动态情况下的确定数据聚类问题.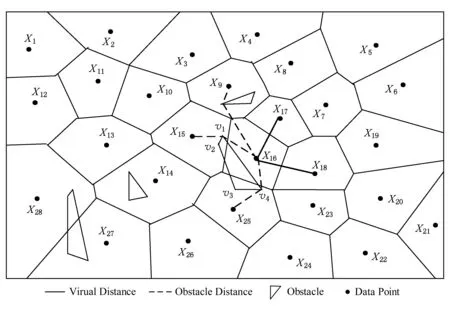

D(vi‖Xj),D(Xi‖vj)+D(vj‖Xj)}.
D(X15‖v4)+D(v4‖X16)}.2 障碍空间中的不确定数据聚类
2.1 静态障碍空间下不确定数据聚类算法
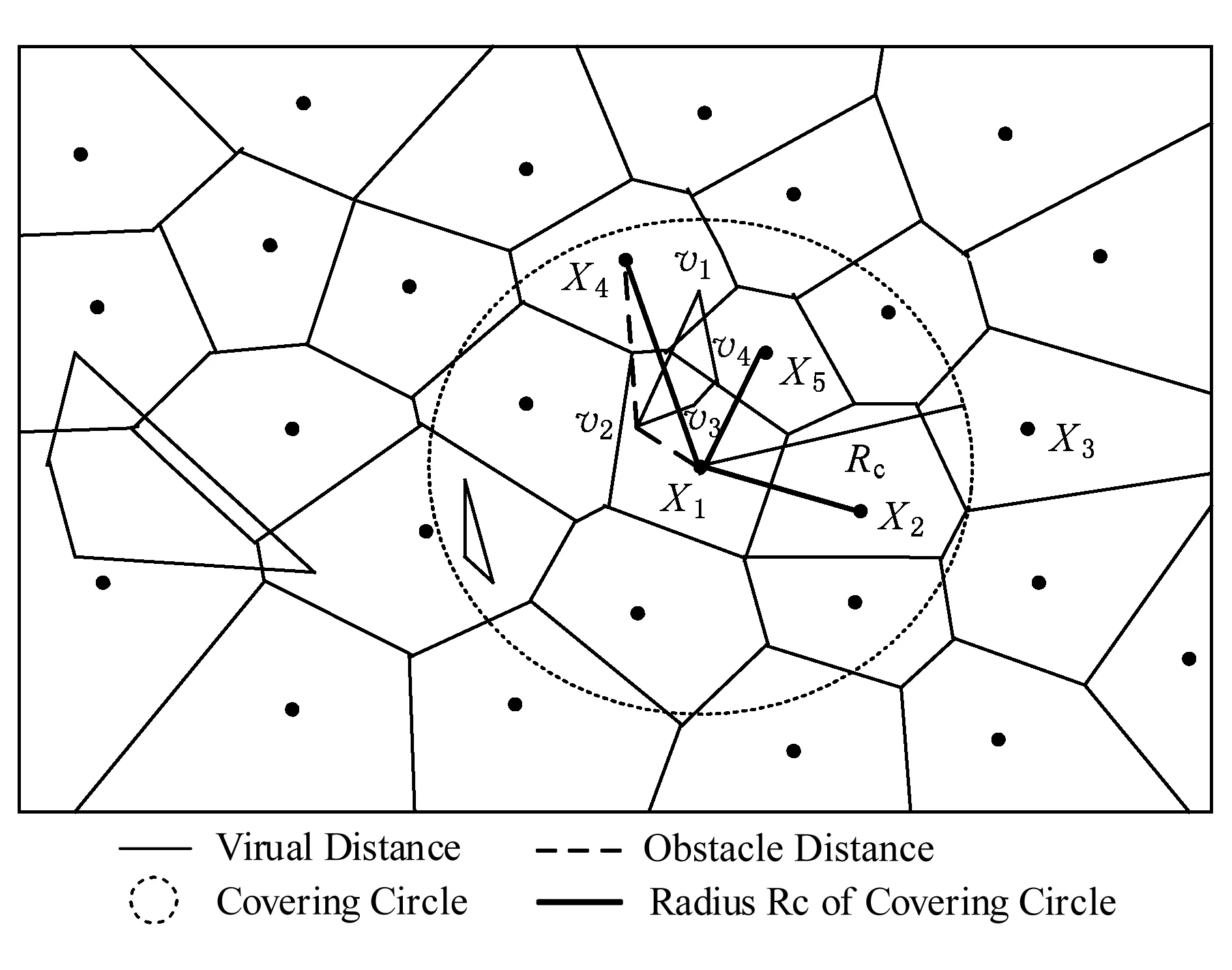
2.2 静态障碍空间中不确定数据精炼算法
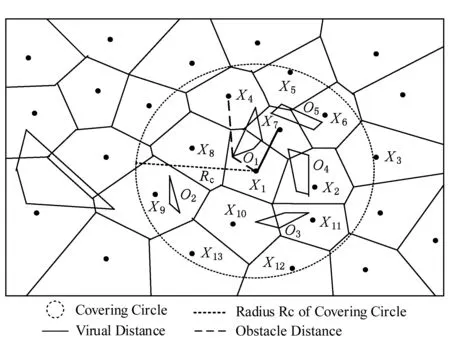
2.3 动态障碍增加情况下不确定数据聚类算法

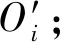
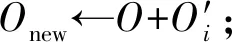




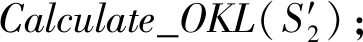
2.4 动态障碍减少情况下不确定数据聚类算法
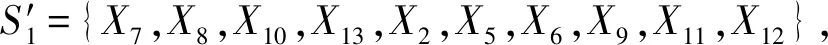

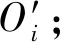
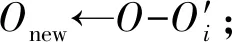


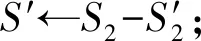
2.5 障碍物动态移动情况下的不确定数据聚类

2.6 障碍空间下的不确定数据聚类算法
3 实验比较与分析



4 结束语

