基于最小二乘配置的光学镜头畸变校正方法
何子清, 葛 超,王春阳
(中国白城兵器试验中心,吉林 白城 137001)
1 引 言
短焦大视场光学测试设备在靶场应用中具有举足轻重的地位。但是由于电荷耦合器件制造误差、镜片曲面误差、各镜片间轴向安装误差以及对中误差等,破坏了摄影中心、待检测点及其像点间的共线关系,产生了畸变[1];并随着视场的增大,畸变值随之增大,虽然不影响图像的清晰度,却严重影响设备的测角精度[2],而测角精度正是检核设备测试能力的重要技术指标,因此,不能忽视畸变对其产生的影响。为了提高光学设备的测角精度,必须采用正确合理的方法对光学镜头进行畸变校正,近些年,众多学者对此做了大量的研究工作[3-10]。
镜头畸变主要有3种:径向畸变、偏心畸变和薄棱镜畸变,靶场光学镜头受径向畸变影响较大,即离镜头中心越远,变形越大。文献[3]提出了一种无需昂贵的器材,便可完成高精度畸变校正的的方法,目前已在靶场使用,该方法以校正点附近若干已知点的畸变值作为观测值,以二次多项式的系数作为估计参数,采用最小二乘估计得到修正模型[3]。该方法虽然能一定程度上抑制畸变产生的影响,但是仍然存在一些问题。比如,校正模型仅是针对局部有效,每个校正点的修正模型均不同,没有整体连续性,无法充分利用已知数据的相关性;另外,这种模型只顾及了畸变的趋势项,而没有考虑随机项。事实上,这种随机项与概率统计意义上的随机误差不同,虽然在数值上呈随机特性,但在光学镜头制作完成后就已经固定了,它对测角精度的影响与在视场中的位置有关,因此,亦可称为似系统误差。这样称呼它是因为,它对已知校正点附近的点有系统性影响,对距离较远的点则呈随机性影响[11]。而文献[3]中的方法将畸变误差作为偶然误差处理,以距离待校正点越近的网格点对其修正值影响越大为依据,虽符合一定的逻辑,但并没有将误差系统性和随机性因素体现在模型中,这显然是不合理的。因此,需要建立一种既能顾及畸变趋势性影响,又能顾及随机性影响的修正模型,另外,由于畸变值形成的曲面较复杂,尤其视场边缘,相对起伏较大,二次多项式难以描述整个视场内畸变值的变化趋势,甚至可能出现“龙格现象”[12]。
为了提高光学设备的测角精度,本文提出一种基于多面函数的最小二乘配置光学镜头畸变校正方法,与其他校正方法不同,该方法既顾及畸变值的趋势特性,又顾及其随机特性,以多面函数代替二次多项式,能更好的反应畸变值曲面的整体连续变化情况;根据拟合残差求出协方差函数的估计参数。最后,利用本文方法和传统方法分别对靶场使用的光学镜头进行校正处理,验证了本文方法的有效性与可行性。
2 原理及数学模型
2.1 靶场畸变校正方法
目前,正在使用的修正模型如下:
Δα=ax2+by2+cxy+dx+ey+f,
(1)
其中,Δα为畸变值,x、y为编码器读数,a、b、c、d、e为系数。
将整个视场以网格的形式进行划分,网格间距根据不同的设备取不同值,选取待校正点附近4×4网格点作为拟合节点,网格点对校正点修正值的影响程度被认为是不一样的,依据到待校正点距离越近影响越大为原则,进行定权处理。由于网格点之间相互独立,因此,权阵上的元素,除对角线外,其他均为0,对角线元素值为网格点与测量点距离的倒数。
根据式(1)建立误差方程:
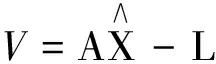
(2)
其中,A为系数矩阵。

在满足VTPV=min条件下,建立法方程:
(3)
式中,P为权矩阵,求解上述法方程,得到函数的系数估计值,模型确定以后,代入编码器读数,即可得到对应位置点的角度修正值。
2.2 基于最小二乘配置的畸变校正模型
根据光学镜头畸变的特点,建立校正模型:
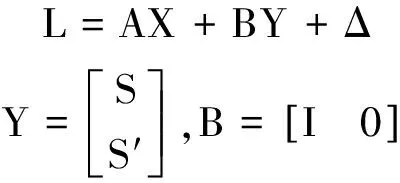
(4)
式中,L为观测向量,即网格点处的畸变值;AX为畸变值曲面连续的整体变化趋势;A为趋势项的系数矩阵;X为非随机参数;如果选二次多项式作为变化趋势项,AX与式(2)中一致;BY表示畸变值曲面不规则的随机部分;S为已测点信号向量,即网格点处畸变值;S′为未测点信号向量,即待校正点处畸变值;Δ为随机误差。
Δ和Y的随机特性为:
(5)
将式(4)改成误差方程的形式:
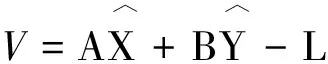
(6)
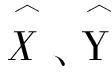
按广义最小二乘原理:
(7)
可得到:
(8)
其中:∑S为网格点的协方差矩阵,∑SS′为网格点与待校正点的互协方差矩阵,∑S′为待校正点的协方差矩阵。协方差矩阵中的元素是根据一个随位置变化的协方差函数计算得到,精确确定协方差函数是最小二乘配置的关键。
在已有的经验协方差函数中,高斯函数应用最广,其表达式如式(9)所示:
σ2(d)=σ2(0)e-K2d2,
(9)
式中:σ2(0)表示距离为0的方差,K为待定的未知参数,d为视场内两点之间的距离。
根据如下公式计算σ2(0)和σ(di):
(10)
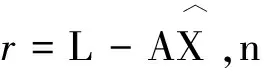
多面函数法在解决不规则的连续曲面函数逼近问题有很好的效果,因此,本文选择用多面函数代替传统的二次多项式对畸变值曲面进行拟合。
假设畸变值曲面是一个连续不规则变化的表面,利用多面函数对其进行逼近[12-13]:
(11)
式中:γi为待求系数,R为核函数,(xi,yi)为核函数的中心点。核函数表达式为:
R(x,y,xi,yi)=[(x-xi)2+(y-yi)2+δ2]ω,
(12)
式中:δ为平滑因子,它的数值大小影响核函数形状;ω为非零实数。在本文中,核函数参数取值为:δ=0.1,ω=0.5。
将式(11)转成矩阵形式,将多面函数融入最小二乘配置中,模型为:
L=Rγ+BY+Δ,
(13)
式中,Rγ表示畸变值曲面的趋势项部分;R为n×m维核函数矩阵;γ为1×m维的待定系数向量;BY为畸变值曲面的随机部分。
根据广义最小二乘原理,解得最小二乘配置解为:
(14)
待校正点的修正值为:

2.3 协方差函数拟合
协方差函数模型的准确性是最小二乘配置的关键。为避免线性化带来的模型误差,文章对高斯函数做一些处理。
对式(9)两边取对数,即可得到如下形式:
(15)
建立平差模型:
(16)
通过最小二乘求得σ2(0)和K。
3 实验数据分析与验证
选用靶场某型炸点坐标测量系统的光学经纬仪作为实验对象,对其进行畸变校正。具体实验步骤如下:图1为在实验室布设的场景图,在平行光管一端放置12W聚光照明灯,作为无穷远目标,尽量使灯光亮点在图像上仅占1到2个像素。调整经纬仪位置,使光轴尽量与平行光管主轴重叠,并将经纬仪整平,水平角置零。将整个视场划分为若干网格,转动经纬仪使光源位于网格点处,单帧采集图像,取光源的像面坐标,并代入式(18)中,得到目标相对经纬仪的方位角和垂直角[14]:
(18)
其中:α0为方位角,λ0为垂直角,f为焦距,α为目标相对经纬仪的方位角,λ为目标相对经纬仪的垂直角。


图1 实验场景图Fig.1 Map of experimental scene
由于经纬仪测角精度为0.5",远远高于设备测角精度40",因此,可假设经纬仪测角误差为零,通过式(18)和(19)联合求得畸变值:
(19)
其中:Δαi为水平方向的畸变值,Δλi为垂直方向的畸变值,αi为目标相对经纬仪的方位角,λi为目标相对经纬仪的垂直角。

(a)水平方向(a) Horizontal direction

(b)垂直方向(b) Vertical direction图2 畸变值曲面的Delaunay三角形网图Fig.2 3D mesh surface figure of distortion
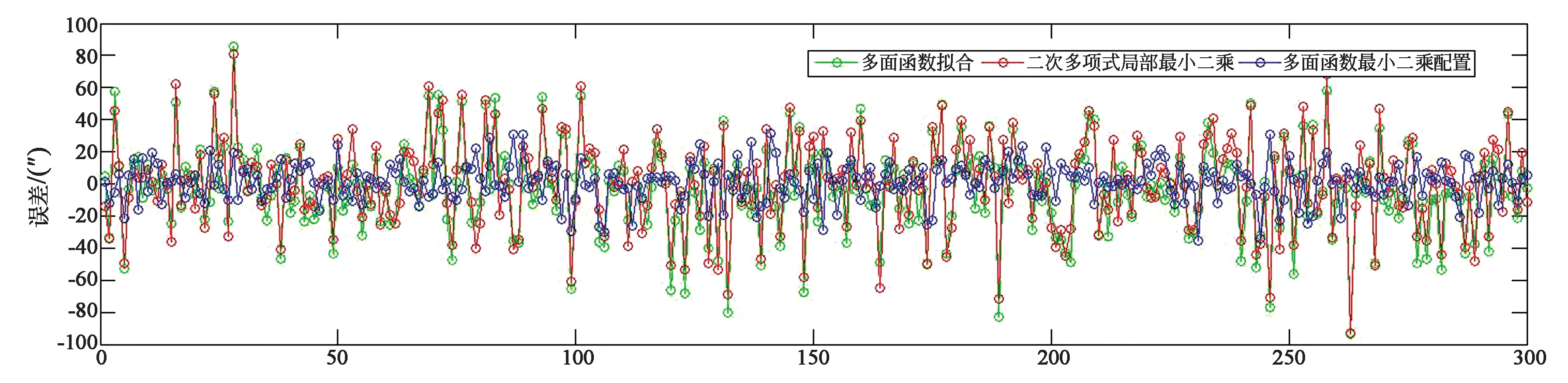
以水平角0°、垂直角90°处为原点,建立二维坐标系,水平方向为x轴,垂直方向为y轴,视场范围为-21° 图3 待校正点在视场内的分布图Fig.3 Distribution map of the points to be corrected in the field 分别用二次多项式局部最小二乘法和本文方法对光学经纬仪设备进行畸变校正。在进行最小二乘配置前,需要确定经验协方差函数,以得到准确的协方差矩阵∑S、∑SS′、∑S′。通过1.3小节介绍的协方差拟合公式(16),求得水平方向的σ2(0)和K为107、0.8,垂直方向的σ2(0)和K为109、0.78。 在镜头视场内随机选取300个点,如图3所示,图中红色“×”代表待校正点,蓝色“+”代表用于多面函数拟合的核函数中心点。 采用3种方案进行畸变校正,具体步骤如下: 方案1:基于二次多项式的局部最小二乘法,该法选取待校正点周围4×4网格点数据作为插值节点拟合趋势项,计算所有待校正点的修正值,将结果与实测畸变值进行求差,得到校正精度; 方案2:多面函数拟合法,该法选取357个网格点作为拟合点,用多面函数拟合畸变值曲面,计算所有待校正点的拟合值,将结果与实测畸变值进行求差,得到拟合精度。 方案3:基于多面函数的最小二乘配置法,该法选取357个网格点作为核函数中心点,用多面函数拟合趋势项,计算所有待校正点的修正值,将结果与实测畸变值进行求差,得到校正精度。 通过以上3种方案对设备进行校正,3种方案的各项指标如表1所示,误差统计如图4所示。 表1 3种方案处理结果统计表 从表1可以得出,方案3的各项指标均优于方案1和方案2。水平方向上,两者的RMS值分别为31.3"、23.1"和11.7",垂直方向上,分别为18.6"、11.2"和7.7"。相比于传统的方法,采用多面函数拟合畸变值曲面,精度在两个方向上分别提高8.2"和7.4",说明多面函数作为曲面的趋势项效果更好;相比于多面函数拟合,基于多面函数的最小二乘配置法的校正精度在两个方向上分别提高11.4"和3.5",说明去除趋势项之后,最小二乘配置会对剩余的不规则随机变化项进行一定的修正,使校正精度更高。以上数据证明了以多面函数拟合趋势项更能反映畸变值的整体连续变化趋势,去除趋势项后得到的随机变化部分也更为平稳。另外,从误差统计图中可以看出,基于多面函数的最小二乘配置法的误差明显小于传统方法和多面函数拟合法,进一步验证了本文方法的有效性。 (a)水平方向(a) Horizontal direction (b)垂直方向(b) Vertical direction图4 3种方案待校正点误差统计图Fig.4 Error statistical chart of the points to be corrected in three method 从实验数据的分析中可以总结出如下结论: (1)采用二次多项式局部最小二乘法,对每个待校正点在小区域内进行校正,存在无法充分利用数据之间的关联性的问题。而采用基于多面函数的最小二乘配置法可以解决上述问题,它是以多面函数的形式,从整体的角度,反映畸变值的整体连续变化趋势。 (2)传统方法只顾及观测值中的偶然误差,而基于多面函数的最小二乘配置法不但能顾及畸变值曲面的趋势项,而且也能顾及不规则变化的随机项。因此,相比于传统方法,以多面函数拟合趋势项更能反映畸变值的整体连续变化趋势,去除趋势项后得到的随机变化部分也更为平稳。 (3)与传统方法相比,基于多面函数的最小二乘配置法不但能较好的反映畸变值的整体连续变化趋势,校正精度也明显优于传统方法。 通过对光学测试设备进行畸变校正,验证了本文方法的可行性与有效性。实验结果证明:本文提出以多面函数代替传统的方法拟合畸变值曲面的变化趋势,能达到更好的效果,另外,最小二乘配置法不但能顾及畸变值曲面的趋势项,而且也能顾及不规则变化的随机项,使待校正点的推估精度更高。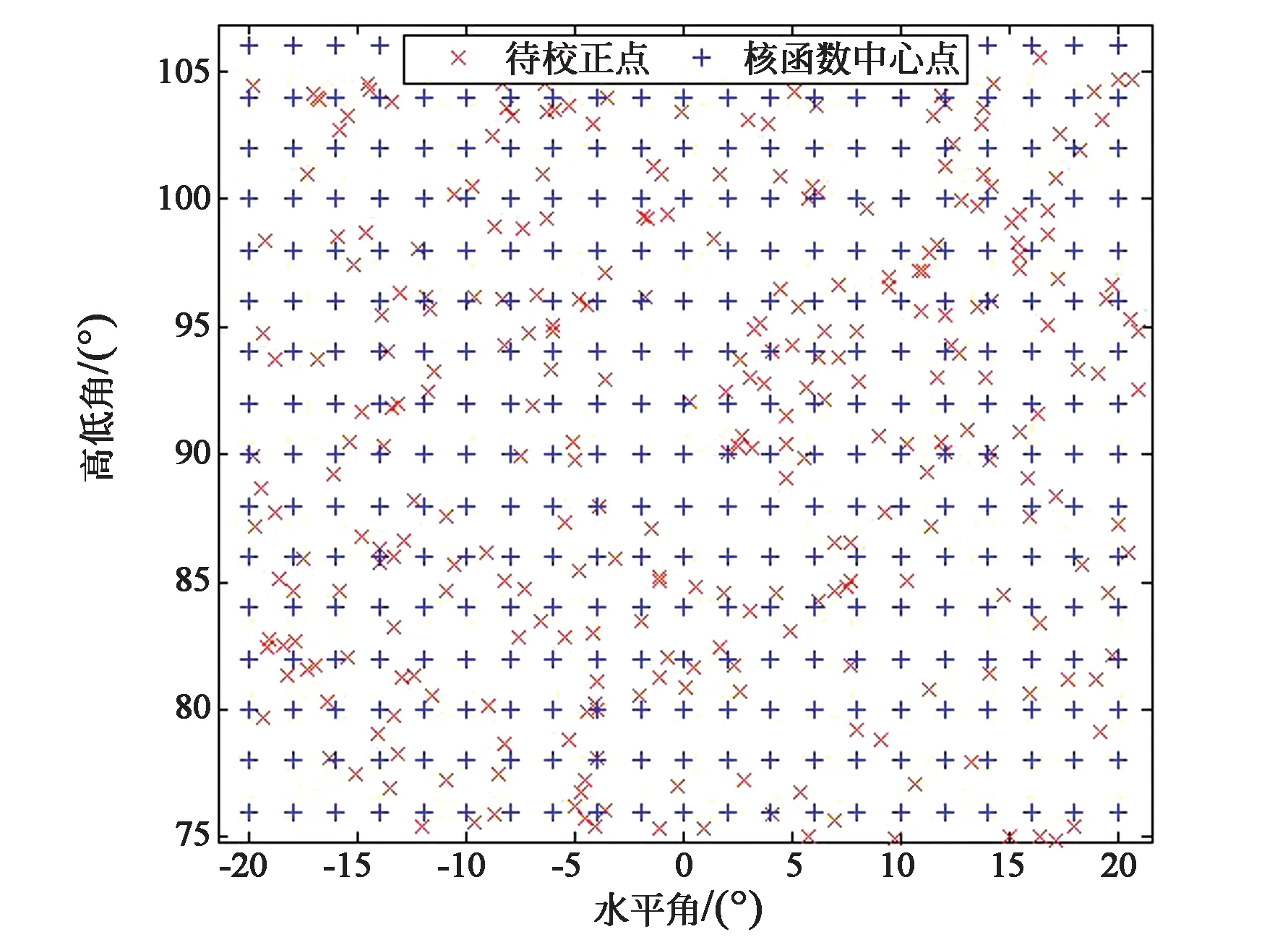

4 结 论

