波浪中过度加速度的非线性时域预报
卜淑霞,顾 民,鲁 江,魏 泽
(中国船舶科学研究中心,江苏省绿色船舶技术重点实验室,江苏 无锡214082)
0 引 言
目前,国际海事组织(IMO)正在制定包括过度加速度在内的船舶第二代完整稳性衡准[1]。过度加速度是指船体横向加速度过大的现象,过大的横向加速度也就意味着较大的横向惯性力矩,会导致货物设备损害和人员伤害。一般来说,较大的初稳性高对船舶稳性是有利的,但初稳性高过大又会导致加速度过大,从而对人员和货物产生不利影响。采用过度加速度作为一种稳性失效模式,可以对船舶的初稳性高进行约束,从而使船舶的初稳性高处于合理的范围。
由于过度加速度造成了集装箱船MV Pacific Adventurer[2],Chicago Express[3],Guayas[4]严重的甩箱和人员伤亡事故,且考虑到当初始GM 值较大时,即便中等幅度的横摇运动也可能会产生横向加速度过大的现象,造成货物的损失或者人员伤亡。另外甲板货物的损失,还会影响其它船舶的正常航行、污染环境等[5-6]。因此IMO 委员会将过度加速度也作为一种稳性失效模式[7]。
已有的事故表明:过度加速度一般发生在压载状态下,此时较大的GM 值,以及由于波浪中失速造成的横摇阻尼较小,会导致船体较高位置处的横向加速度过大;在发生过度加速度现象时,事故船都产生了超过30°的横摇幅值;由于过度的稳性以及周期较短,导致最大的横向加速度都超过了1.0 g;发生事故时船体速度都较低,据报道,当Chicago Express 以及Guayas 这两起事故发生时,航行速度特别低,仅在2~4 kns 左右[2-4]。
从上述分析可以看出,在压载或者接近压载、低航速下较容易发生过度加速度,且会伴随着较大的横摇幅值。因此,本文研究中,选取了某集装箱船的压载状态,以及横浪、零航速的工况,此时容易发生共振横摇,进而容易引起过度加速度。
由于过度加速度这一稳性失效模式提出的时间较短,所以公开的研究成果较少。过度加速度的研究涉及到对大幅横摇运动的准确预报以及对加速度衡准值的准确判断,并且目前IMO 第二代完整稳性衡准制定中,过度加速度的薄弱性衡准提案主要由中国、德国制定[8]。因此,目前急需建立一套合理、可行的直接评估方法。
本文研究目的在于针对过度加速度稳性失效模式建立一套合理、完善的稳性直接评估方法,并验证目前中国和德国联合提出的薄弱性衡准草案[9]的可行性。文中首先基于三维时域混合源法,对比分析了不同耦合方程在大幅横摇运动求解中的适用性,在此基础上,形成过度加速度的直接评估方法;其次,以4000TEU 集装箱为对象,开展波浪中加速度的模型试验,验证文中采用方法的有效性;然后,采用直接评估方法评估了目前薄弱性衡准中横向加速度简化计算方法的可行性。
1 数学模型与计算方法
1.1 三维时域混合源法
本文采用三维时域混合源法进行过度加速度的直接数值预报,该三维时域混合源法在数值求解中引入了控制面SC,将流场分为内域I 和外域II。内域I 是由船体湿表面Sb、部分自由液面Sf1和控制面SC包围的闭合区域,该区域内采用Rankine 源。外域II 由控制面、剩余自由液面Sf2和无穷边界S∞组成,该计算域内采用时域Green 函数。该方法理论上可以保留Rankine 源易于计算、可以得到近场定常速度势,以及Green 函数法仅需在物体表面进行离散,函数自动满足线性自由表面和远场辐射条件的优点,消除了两者的缺点,在计算非线性大幅运动时具有明显的优势[10-11]。
在计算中主要采用三个坐标系,一个是大地坐标系O-XYZ,一个是参考坐标系o′-x′y′z′,一个是船体坐标系G-xyz。流场分布、坐标系示意图以及船体网格分布如图1 所示。

图1 计算域划分和船体网格示意图Fig.1 Domain definitions and meshes schematic
(1)大地坐标系O-XYZ:X 轴指向船首为正,Y 轴指向左舷为正,Z 轴垂直向上为正,原点位于平均吃水线处,该坐标系不随船体运动。
(2)参考坐标系o′-x′y′z′:x′轴指向船首为正,y′轴指向左舷为正,z′轴垂直向上为正,原点位于平均吃水线处,初始时刻与大地坐标系在同一位置,随船体速度前进。
(3)船体坐标系G-xyz:x 轴指向船首为正,y 轴指向左舷为正,z 轴垂直向上为正,原点位于船舶重心,该坐标系随船运动。
假设流体无粘、无旋和不可压缩,水深为无限水深,则流场非定常的速度势可表示为:


则内域I 中Rankine 源的边界积分方程如下:

其中:ΦI是内域I 总扰动速度势;G=1/rpq为简单格林函数,p (x, y, z )为场点,q (ξ, η, ζ )为源点,rpq=是内域I 边界的外法线向量。

为了求解该定解问题,我们引入如下的时域格林函数:
外域II 中使用时域格林函数,面元分布在控制面SC上,边界积分方程如下:


其中:ΦII为内域II 总扰动速度势,w(τ)是控制面的水线面,VN是w(τ)的法向速度。
控制面随船体一起运动,因此在控制面上内外域连续,采用面元法对边界积分方程(3)和(6)进行数值离散,可以获得当前时刻船体湿表面积Sb上的ΦI,自由表面Sf1上的,以及控制面SC上的ΦI和然后就可以利用物面上的ΦI,通过伯努利方程计算船体表面的压力以及相应的水动力,利用内域I 中线性自由面获得下一时刻整个流场的扰动势和下一时刻内域的速度势ΦI。
对船体平均湿表面积Sb上的源强积分即可得到船体湿表面上的扰动速度势ΦI,且已知入射波速度势Φw,最后通过伯努利方程可得到相应的压力项:

求得每个面元控制点的压力后,对每个面元积分即可求得作用于该面元上的流体作用力F 和力矩M。

1.2 数学模型
过度加速度的直接数值预报与船舶大幅运动的求解密切相关。考虑到横浪中大幅运动的特点,文中分别采用了3DOF(垂荡—横摇—纵摇)耦合方程和4DOF(横荡—垂荡—横摇—纵摇)耦合方程进行数值预报。
3DOF 耦合方程:

4DOF 耦合方程:

其中:m 为船舶质量;Ixx为横摇惯性矩;Iyy为纵摇惯性矩;Aij、Bij为附加质量和阻尼系数;x2为横荡位移;x3为垂荡位移;θ 为纵摇;φ 为横摇;N1、N2为线性和平方的横摇阻尼系数,采用模型试验数据。FFK+H为FK 力和静水力,通过对瞬时湿表面压力积分得到;FDF为绕射力,沿船体平均湿表面积分得到。船体运动的偏微分方程利用Runge-Kutta 方法求解。
在数值模拟中规则波采用和模型试验中一致的简谐波,不规则波采用规则波线性叠加的形式。横摇方向惯性矩和附加惯性矩采用如下公式计算:
1.3 横向加速度简化计算

在IMO 最新的过度加速度薄弱性衡准提案中[9],中国和德国联合提出了采用公式(12)所示的简化公式计算船体任意位置处的加速度,该公式是将垂荡、纵摇、首摇的影响简化为某一系数。本文在研究中首先通过模型试验验证了该公式的可靠性。

其中:kL是无因次的垂向加速度和首摇运动的影响系数,与计算点的纵向位置有关,可利用公式(13)求解。

其中:x 是从船艉到计算点的纵向距离(m);L 是船长(m)。
1.4 横向加速度直接计算
过度加速度是指横向加速度较大的现象,较高位置的舷侧处加速度会比较大,因此过度加速度一般衡量驾驶室或者舰桥等位置处的加速度。加速度求解示意图如图2 所示,可以看出,横向加速度也就是图中沿甲板面的加速度,计算公式如下所示:


图2 横向加速度计算示意图Fig.2 Schematic for the calculation of lateral acceleration
其中:al和an是分别为沿甲板方向和垂直于甲板面的加速度分量;aV和aH分别为P 点沿垂直方向和水平方向的加速度分量,可根据船体重心处的运动,采用如下公式计算:

2 模型试验
2.1 试验模型
模型试验在中国船舶科学研究中心耐波性水池中进行,水池主尺度:长69 m、宽46 m、深4 m,该水池可进行任意浪向下的波浪模型试验。在水池相邻两边布置了从国外引进的三维摇板式造波机,造波机可模拟规则波、长峰不规则波和短峰波。试验采用4000TEU 集装箱船,模型缩尺比为1:63.0,模型照片如图3 所示,主要参数如表1 所示。

图3 4000TEU 集装箱船模型照片Fig.3 The model test photos of the 4000TEU containership

表1 4000TEU 集装箱船主尺度(缩尺比1/63.0)Tab.1 Principal particulars of the 4000TEU containership(Scale:1/63.0)
2.2 试验方法
过度加速度模型试验采用定点模式,在90°横浪中进行试验。由计算机实时记录船模遭遇的波浪历程,采用陀螺对模型的横摇运动进行测量,垂荡运动采用重心处的加速度积分得到。3 个测点的横向加速度通过加速度传感器进行测量,测点坐标列于表2 中。测点在模型上的布置分别为重心左舷处(P1)、驾驶室右舷处(P2)以及模型艉部0 站右舷处(P3)。

表2 三个测点的位置Tab.2 Definition for three measuring points
2.3 波浪条件
规则波中选取的试验波浪条件为11 组横浪,波长/船 长 分 别=0.2、0.3、0.4、0.6、0.8、1.0、1.2、1.4、1.6、1.8 和2.0,波陡固定为0.03。不规则波波浪条件如表3 所示。采用ITTC 双参数谱进行模拟,谱密度如下式所示:


表3 不规则波波浪条件Tab.3 Wave conditions in irregular waves
其中:H1/3为有义波高;T01为波浪特征周期;ω 为波浪圆频率。
3 结果与分析
3.1 横摇幅值计算结果与分析
基于三维时域混合源法分别在规则波和不规则波中,开展波浪中船舶大幅运动和加速度的数值模拟。图4 为规则波中不同波浪条件下的横摇幅值和垂荡幅值数值模拟结果与模型试验结果的对比。从对比结果可以看出,4DOF 数学模型整体上比3DOF 数学模型计算结果准确,但是在共振横摇位置处,4DOF 数学模型计算结果略微偏小,误差约为14.5%。分析原因主要是共振横摇位置处,横摇幅值随其它因素,如波高、横摇惯性矩等的影响较为敏感,根据模型试验测量得到的静水自由横摇衰减曲线校对横摇惯性矩,重新计算,结果如图5(左)所示(4DOF-Tune),可以看出惯性矩校对后,共振处的横摇幅值呈现较为明显的变化,横摇幅值的计算误差缩小为0.87%,并且此时发生共振的频率与模型试验基本一致;将波幅增加5%,如图5(右)所示,可以看出共振处横摇幅值的计算误差缩小为6.9%。另外,本文在线性和非线性横摇阻尼系数计算中采用初始横摇幅值15°的自由横摇衰减曲线,不同初始横摇幅值对应的横摇阻尼也会对横摇幅值产生影响。

图4 规则波中横摇和垂荡运动幅值对比Fig.4 Comparisons of the amplitudes of roll and heave motions in regular waves

图5 横摇惯性矩和波高对横摇幅值的影响(左:横摇惯性矩;右:波幅)Fig.5 Influence of roll inertia moment and wave amplitude on roll amplitudes(Left:roll inertia moment;Right:wave amplitude)

图6 不规则波中横摇和垂荡运动有义幅值对比Fig.6 Comparisons of the amplitudes of roll and heave motions in irregular waves
图6 为不规则波中不同波浪工况下的横摇有义幅值和垂荡有义幅值数值模拟结果与模型试验结果的对比,图中横坐标No.表示表3 中所示的波浪工况。从图中可以看出,4DOF 数学模型整体上比模型试验结果稍微偏小。从目前对比结果可以看出,3DOF 数学模型计算得到的结果整体上比试验值偏大,从工程评估的角度来看,安全裕度更大。
3.2 IMO 加速度简化计算方法计算结果与分析
针对IMO 薄弱性衡准提案中加速度的简化计算公式(12),本文基于上述横摇幅值的计算结果和模型试验结果验证了该公式的可靠性。考虑到对于特定的位置,简化公式(12)的计算主要取决于横摇幅值,因此文中分别基于模型试验直接测量得到的横摇幅值、基于3DOF 数学模型计算的横摇幅值、基于4DOF 数学模型计算的横摇幅值,验证了简化公式(12)计算加速度的可靠性,对比结果见图7-9。图中Exp:代表模型试验直接测量得到的横向加速度;Exp-sim:代表公式(12)中的横摇幅值由模型试验直接测量得到;3DOF-sim:代表公式(12)中的横摇幅值由3DOF 数学模型计算得到;4DOF-sim:代表公式(12)中的横摇幅值由4DOF 数学模型计算得到。

图7 位置P1 处基于简化方法的横向加速度对比(左:规则波;右:不规则波)Fig.7 Comparison of lateral accelerations by simplified method at position P1(Left:regular wave;Right:irregular wave)

图8 位置P2 处基于简化方法的横向加速度对比(左:规则波;右:不规则波)Fig.8 Comparison of lateral accelerations by simplified method at position P2(Left:regular wave;Right:irregular wave)

图9 位置P3 处基于简化方法的横向加速度对比(左:规则波;右:不规则波)Fig.9 Comparison of lateral accelerations by simplified method at position P3(Left:regular wave;Right:irregular wave)
从图中所示的结果可以看出,规则波和不规则波中基于简化公式计算的结果均比模型试验直接测量得到的加速度略微偏大,这符合过度加速度薄弱性衡准评估的要求,即在满足一定精度的前提上,也要满足一定的安全裕度,因此,目前的简化公式满足IMO 薄弱性衡准的要求。
3.3 横向加速度直接计算结果与分析
本文基于公式(14)所示的直接计算方法,分别采用3DOF 数学模型和4DOF 数学模型计算得到的船体重心处的运动、速度、加速度计算结果,结合刚体运动理论,直接对三个测点处的横向加速度进行了数值模拟。规则波中不同横向位置处的加速度数值计算结果与模型试验结果对比如图10(左)-12(左)所示。从计算结果可以看出,当校对横向惯性矩使共振位置与模型试验一致时,4DOF 数学模型可以高精度地再现模型试验结果;而3DOF 数学模型计算结果略微偏大,这主要是由于目前3DOF 计算得到的横摇幅值偏大。从图中也可以看出,三个测点在某些工况下,横向加速度可能接近7.0 m/s2,这已经超过了人员能承受的范围,处于非常危险的状态。另外,从三个测点的模型试验结果以及计算结果可以看出,P2 处的加速度最大,因为该点选取在驾驶室处,位置最高,也最有可能发生过度加速度现象。计算结果也说明船舶在压载状态下有可能发生过度加速度现象,因此,在设计阶段应该选取合理的初稳性高,以防止过度加速度发生。
考虑到过度加速度衡准是采用概率方法进行评估,也就是需要结合海浪波浪谱,评估不规则波中船舶横向加速度的特性[1]。因此,不规则波中横向加速度的数值预报精度对于衡准的制定具有重要意义。本文进一步对比了不规则波中横向加速度的有义幅值,如图10(右)-12(右)所示。从对比结果可以看出,文中所采用的三维时域混合源法可以较好地计算不规则波中的横向加速度。从目前模型试验结果可以看出,目前所示的不规则波中横向加速度的有义幅值与规则波中峰值处的横向加速度几乎一致,最大横向加速度可达到7.0 m/s2,说明在船舶设计阶段,对加速度进行有效的评估十分必要。
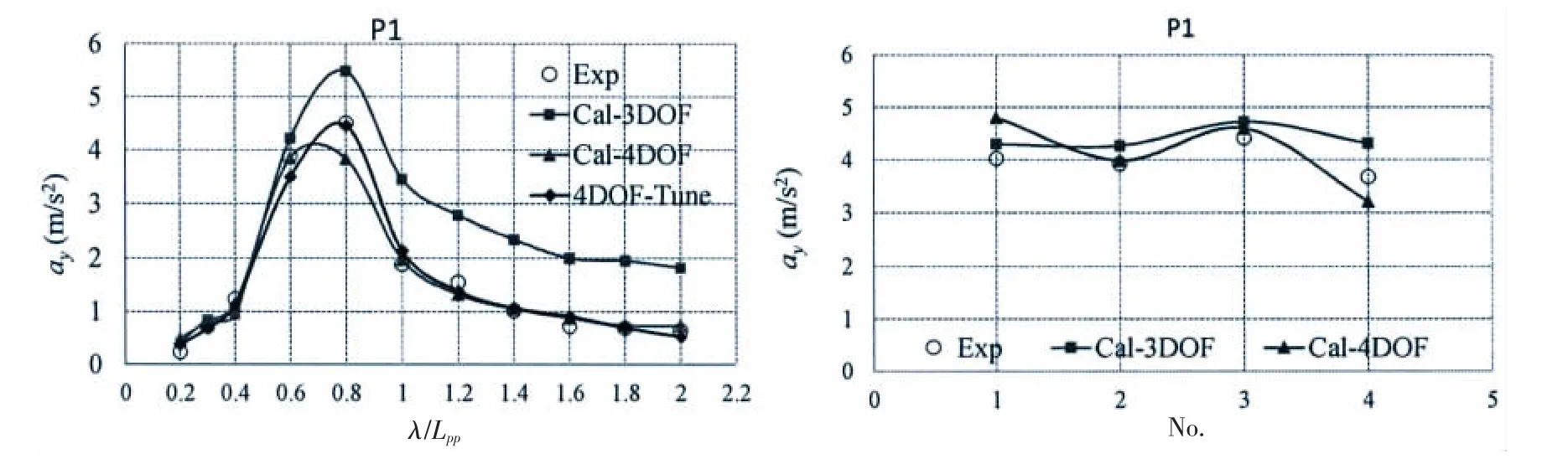
图10 位置P1 处的横向加速度对比(左:规则波;右:不规则波)Fig.10 Comparison of lateral accelerations at position P1(Left:regular wave;Right:irregular wave)

图11 位置P2 处的横向加速度对比(左:规则波;右:不规则波)Fig.11 Comparison of lateral accelerations at position P2(Left:regular wave;Right:irregular wave)

图12 位置P3 处的横向加速度对比(左:规则波;右:不规则波)Fig.12 Comparison of lateral accelerations at position P3(Left:regular wave;Right:irregular wave)
3.4 影响因素分析
横向加速度与船体横摇幅值以及计算点的位置有关。以位置P2 为基准,固定纵向和横向位置,分别选取四个高度(H1=19.87 m,H2=30.73 m,H3=45.0 m,H4=60.73 m),计算不同波浪条件下的横向加速度。从图13(左)所示的计算结果可以看出,横向加速度随计算高度的增加而不断变大。将每个高度对应的最大横向加速度(共振横摇处)取出,绘制成图13(右),可以看出,随着高度的增加,横向加速度基本呈现线性变化,与简化公式(12)中的规律一致。

图13 横向加速度随高度的变化(左:不同波浪条件;右:固定波浪条件)Fig.13 Lateral accelerations along with height(Left:different wave conditions;Right:constant wave condition)
再以位置P2 为基准,选取不同的纵向位置以及不同的横向位置,计算不同位置处横摇共振处的横向加速度,计算结果如图14 所示。图14(左)为横向加速度随纵向位置(距离尾垂线)的变化,图14(右)为横向加速度随横向位置的变化,可以看出纵向和横向位置的变化对横向加速度的影响较小。在简化公式(12)中,横向加速度的计算与横向位置无关,该简化公式中虽然有纵向位置项,但从公式(13)可以看出,与纵向位置有关的kL值基本位于1 附近,也就说明横向加速度与计算点的纵向和横向位置关系不大,与目前直接评估结果得到的规律一致。

图14 横向加速度随纵向和水平位置的变化(左:纵向位置;右:横向位置)Fig.14 Lateral accelerations along with longitudinal and horizontal positions(Left:longitudinal positions;Right:horizontal positions)
4 结 论
本文针对过度加速度稳性失效模式,提出了一种采用三维时域混合源法计算船舶在规则波和不规则波中大幅横摇运动和横向加速度的直接数值预报方法,并开展模型试验,对数值预报方法进行了验证。得出如下结论:
(1)本文采用的三维时域混合源法可以较好地预报规则波和不规则波中船舶的大幅横摇运动以及任意位置处的横向加速度,可用于波浪中过度加速度的稳性直接评估。
(2)横向加速度的准确预报取决于大幅横摇运动的预报精度,考虑横荡影响之后的4DOF 耦合方程预报精度要大于3DOF 耦合方程的预报精度。
(3)固定船舶的装载,最大横向加速度位于共振横摇位置处,且随计算点的高度基本呈线性增加,但与计算点的纵向和横向位置关系不大。
(4)中国和德国联合提出的IMO 过度加速度薄弱性衡准中采用的横向加速度简化公式,计算结果比直接评估结果和模型试验略微偏大,符合IMO 薄弱性衡准的要求,因此可用于IMO 过度加速度的薄弱性衡准计算。

