形状调配中带参数的过渡曲线设计
严兰兰,樊继秋,马 力
形状调配中带参数的过渡曲线设计
严兰兰1,樊继秋1,马 力2
(1. 东华理工大学理学院,江西 南昌 330013;2. 湖北省麻城市第一中学,湖北 麻城 438300)

曲线设计;过渡曲线;形状调配;形状调整
形状调配,又称为形状混合,也就是曲线曲面混合,是几何造型领域中的一个重要研究课题,也是曲线曲面控制设计中的一种常用技术[1],同时也是计算机关键帧动画的核心技术。形状调配一般是指在两个关键帧中插入若干中间帧,产生连续平滑的过渡[2]。在已有文献中,形状调配指的是由两条(张)给定的曲线(曲面)通过形状混合的方式生成一条(张)新的曲线(曲面),新曲线将给定曲线中一条的首端与另一条的尾端光滑地连接起来,新曲面将给定曲面沿同一参数方向的两条边界曲线光滑地连接起来,要求新曲线(曲面)在端点(边界)处与给定曲线(曲面)重合,并且在端点(边界)处满足一定的参数连续或几何连续条件[1,3],本文讨论的即是该形状调配。根据相关文献给定的曲线曲面可以称为基曲线曲面、待混合曲线曲面,或者待过渡曲线曲面,新曲线曲面则称为混合曲线曲面,或者过渡曲线曲面,本文采用基曲线和过渡曲线来指代给定曲线和新曲线。形状调配,实际上也可以通过插值的方式来实现,但是传统的插值方法,如Hermite插值、参数连续C插值和几何连续G插值等方法,往往只考虑端点处的局部几何信息,而混合方法由于可以较好地结合基曲线曲面的全局几何信息,因此得到的曲线曲面形状往往更加真实有效[4]。
在形状调配中,基曲线的类型是多种多样的。张宏鑫和王国瑾[5]给出了保持一阶、二阶几何连续的Bézier曲线形状调配条件以及改进的调配方法。刘华勇等[6-8]给出了在线性混合过程中,一阶、二阶参数拟连续的保持条件,得出了3种不同类型的Bézier-like曲线在形状调配中保持一阶、二阶参数拟连续性特征的方法。刘华勇等[9]讨论了文献[8]中的Bézier-like曲线在线性混合过程中保持一阶、二阶几何连续的条件以及方法。由于文献[6-9]中的基曲线都是带形状参数的Bézier-like曲线,因此相应的过渡曲线都可以在不改变端点处连续性的前提下调整形状。但同时注意到,如果附加一个前提条件,即基曲线形状固定,那么文献[6-8]中构造的过渡曲线实际上是不具备形状可调性的。原因在于其过渡曲线之所以形状可调,是因为基曲线形状可调,改变其形状参数,基曲线形状发生变化,进而带动过渡曲线形状的改变。然而对于文献[9]而言,即使规定基曲线形状固定,由其构造的过渡曲线形状依然可以调整,这是因为所给过渡曲线的方程中包含了不依附于基曲线的调节参数。虽然文献[9]中的过渡曲线具备相对于固定基曲线的形状调整能力,但其基曲线是指定类型的Bézier-like曲线。考虑到在实际应用中,基曲线的模型往往并非特定,因此,要想得到适用面更广的形状调配方法,必须突破对基曲线类型的限制。
李凌丰等[10]提出基于势函数与Metaball技术的过渡曲线构造方法,其采用一种6次多项式势函数来构造过渡曲线,由该方法构造的过渡曲线对基曲线的种类没有限制,所得过渡曲线形状自然,但过渡曲线在两个端点处与基曲线之间只能达到拟1连续,并且过渡曲线不具备相对于固定基曲线的形状调整能力。基于严兰兰等[11]所给带形状参数的Bézier曲线模型,李军成等[3,12]采用相同的方法构造了一种带参数的7次多项式调配函数,任给两条参数曲线作为基曲线,由该调配函数构造的过渡曲线在两个端点处与基曲线之间可以达到拟2连续,而且过渡曲线的形状还可以在不改变基曲线形状以及过渡曲线与基曲线在端点处连续性的情况下自由调整。也就是说,文献[3]和文献[12]中的过渡曲线不仅兼具了文献[9]和文献[10]中过渡曲线的优点,而且还提高了文献[10]中过渡曲线在端点处的连续性。
为了保留文献[3]和文献[12]中形状调配方法的2个优点:①对基曲线的类型不做限制;②过渡曲线形状可调,同时又进一步提升过渡曲线在端点处与基曲线之间的连续性。本文打算构造一种新的含参数的多项式调配函数,使得对于任意给定的基曲线,由该调配函数构造的过渡曲线在端点处与基曲线之间至少可以达到拟3连续,而且过渡曲线的形状还可以在不改变基曲线形状的前提下自由调整。
1 预备知识
1.1 问题描述
从形状调配的应用背景出发,过渡曲线的构造问题可以描述为:已知平面上两条参数曲线1()与2(),1()的起点记为,2()的终点记为,希望构造一条曲线(),以为起点,以为终点,如图1所示。要求曲线()的形状取决于曲线1()与2()的形状,并要求曲线()在两个端点和处分别与曲线1()、2()之间满足一定的拟连续性要求。

图1 过渡曲线的构造
称1()与2()为基曲线,称()为过渡曲线。文献[12]给出过渡曲线的方程为

式(1)表明过渡曲线为基曲线的加权组合,当基曲线给定时,过渡曲线的形状和性质完全取决于调配函数的性质。
1.2 Bernstein基函数的相关结论
定理1. Bernstein基函数具有下列性质:
(6) 端点导数。次Bernstein基函数在端点处的阶导数为


证明:性质(1)~(5)在教材[13]中可以直接找到。下面推导性质(6)。



又文献[13]中给出


对照式(5)和式(7)即可得出式(2)。将式(8)改写为

对照式(6)和式(9)即可得出式(3)。 证毕。
2 调配函数及其性质
2.1 调配函数需满足的条件
将式(1)整理成

由Leibniz公式可得

要使过渡曲线()在两个端点处与曲线1()和2()之间满足拟3连续要求,必须

其中,=0,1,2,3。
由式(10)可知,若调配函数()在两个端点处满足条件
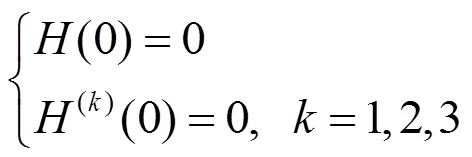
以及

则有式(11)成立。因此式(12)和式(13)给出了为使过渡曲线在端点处达到拟3连续,调配函数需满足的条件。
2.2 不含参数的调配函数
由2.1节的分析可知,为了使式(1)给出的过渡曲线在两个端点处达到拟3连续,必须要求调配函数()满足式(12)和式(13)给出的所有条件。条件一共有8个,当调配函数()为7次多项式时,其未知系数一共有8个,恰好与条件个数一致,因此将其条件转化为关于未知系数的方程组,有望得到唯一解。
多项式调配函数()既可以用幂基表达,也可以用Bernstein基函数表达。式(12)和式(13)涉及到调配函数()的导数,虽然幂基求导方便,但用幂基表示时,所得方程组的解要通过一定计算才能得出。
将调配函数()用Bernstein基函数表达,设
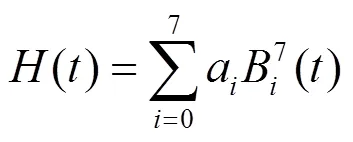
由式(2)和式(12)及式(14)可得
由此推出
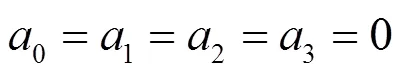
由式(3)和式(13)及式(14)可得
由此推出
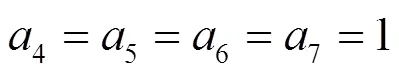
将式(15)和式(16)所得结果代入式(14),得到

定理2.由式(17)得到的调配函数()具有下列性质:
(1) 端点性。即式(12)和式(13)成立。
(2) 对称性。即()+(1-)=1。
(4) 单调性。即()关于单调递增。
证明:
(1) 由()的构造过程可知,端点性显然成立。
(2) 由Bernstein基函数的对称性可得

再由Bernstein基函数的规范性可得
(4) 由Bernstein基函数的求导公式可得


图2给出了调配函数()的图形,从图中可直观看出其端点性((0)=0与(1)=1)、中点性、单调性、有界性是成立的。

图2 调配函数H(t)的图形
2.3 含参数的调配函数
在2.2节中,从调配函数需满足的端点条件出发,得到了同时具备端点性、对称性、中点性、单调性、有界性的调配函数()。
由于()的表达式中不包含任何自由参数,因此以其作为调配函数时,按照式(1)构造的过渡曲线形状由基曲线唯一确定。为了实现在不改变基曲线的前提下,过渡曲线的形状仍然可以调整的目标,需要在调配函数中引入调节参数。
为了避免混淆,将融入了参数的调配函数记作()。在已有()的表达式中融入参数并不困难,但注意在引入参数的同时,不可以破坏调配函数已经具备的性质。
为了得到满足预期目标的调配函数(),将式(17)所给()的表达式升阶两次,得到
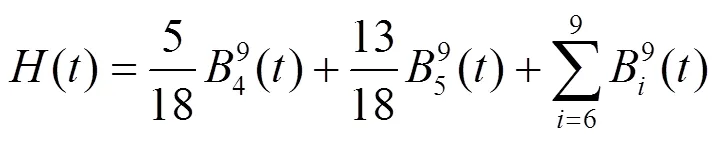
在式(18)的基础上,令
因为()已具备中点性,所使()满足中点性,必须


定理3. 由式(19)给出的调配函数()具有下列性质:

证明:
(1) 若记

则有

易知

由式(21)和式(22)及()的端点性可知,()同样满足端点性。

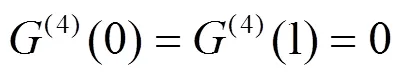
(2) 由式(20)可得

由式(20)和式(23)可得

由式(21)和式(24)及()的对称性可知,()同样满足对称性。
(3) 由()的构造过程可知,中点性显然成立。
(4) 将Bernstein基函数的求导公式用于式(19),可得

又由式(20)和式(21)可得

(5) 由(0)=0,(1)=1,以及()关于的单调性可知,有界性成立。
(6) 在式(25)所得结果的基础上再求一次导数,得到

记
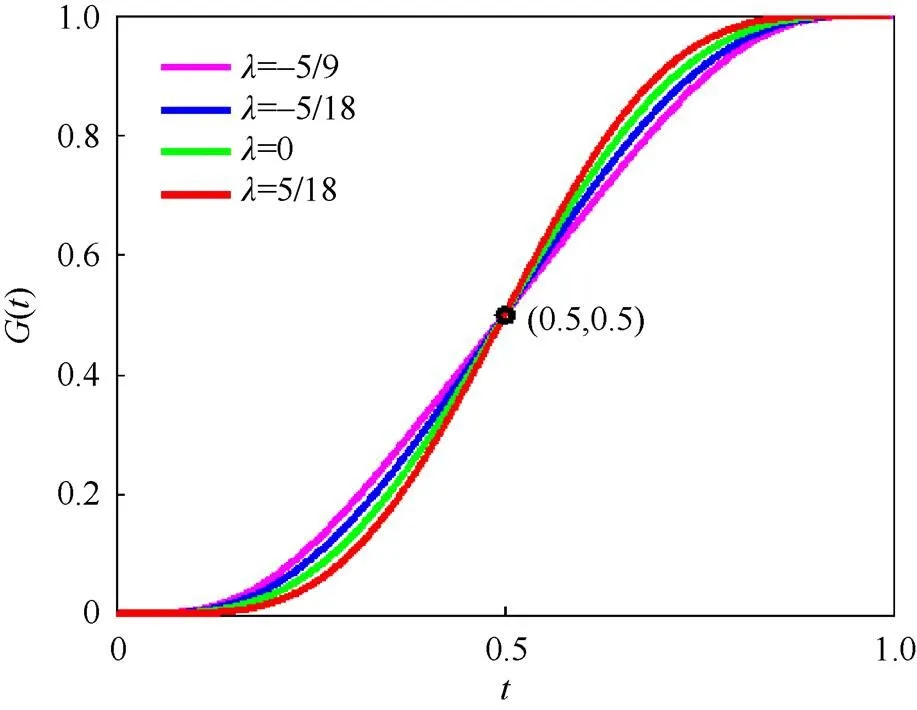
图3 拐点唯一的调配函数G(t)

图4 单调递增的调配函数G(t)
3 过渡曲线
3.1 过渡曲线的特征
任给两条基曲线1()与2(),取式(19)所给()作为式(1)中的调配函数,下面根据调配函数()的性质来分析所得过渡曲线()的特征。

(2) 由()的中点性可知



3.2 过渡曲线的图例

图5 C-形过渡曲线(基曲线上凸下凹)

图6 S-形过渡曲线(基曲线上凸下凹)

图7 C-形过渡曲线(基曲线上凸下凸)

图8 S-形过渡曲线(基曲线上凸下凸)

图9 C-形过渡曲线(基曲线上凹下凹)

图10 S-形过渡曲线(基曲线上凹下凹)


图11 本文方法与文献[3]方法的比较
4 结束语
在对现有文献优缺点进行分析的基础上,以进一步提高文献[11]和文献[12]中过渡曲线在端点处的连续性为目标,本文展开了相关研究。首先预设一个连续阶,然后采用逆向思维法,从过渡曲线的表达式出发,反推出调配函数需满足的一些最基本的性质。将调配函数表达成Bernstein基函数的线性组合,由调配函数的基本性质,结合Bernstein基函数的相关结论,得出满足预设连续阶的不含任何调节参数的调配函数初步表达式。为了在调配函数中引入参数,同时又保持调配函数已经具备的一些良好的性质,对调配函数的初步表达式进行升阶,进而引入参数,得出调配函数的最终表达式。归功于Bernstein基函数完善的理论和良好的性质,调配函数的整个构造过程未涉及复杂繁琐的计算,所得调配函数也很自然地具备一些预期的性质,因此可以说该调配函数的构造方法既简单又高效,而且还具有一般性,仿照上述步骤可以构造出能使过渡曲线在端点处达到更高连续阶的调配函数。下一步的研究工作可以从2个方面展开:①将本文的结果一般化,即探讨如何构造在端点处可以与基曲线之间达到任意C连续并且形状可调的过渡曲线;②将本文用于构造过渡曲线的方法推广至过渡曲面的构造。
[1] 李重, 金小刚, 马利庄, 等. 多项式混合曲线曲面方法构造[J]. 计算机辅助设计与图形学学报, 2009, 21(5): 579-583.
[2] SEDERBERG T W, GREENWOOD E. A physically based approach to 2-D shape blending [J]. ACM SIGGRAPH Computer Graphics, 1992, 26(2): 25-34.
[3] 李军成, 宋来忠, 刘成志. 形状调配中带参数的过渡曲线与曲面构造[J]. 计算机辅助设计与图形学学报, 2016, 28(12): 2088-2096.
[4] SONG Q Z, WANG J Z. Generating Gnparametric blending surfaces based on partial reparameterization of base surfaces [J]. Computer Aided Design, 2007, 39(11): 953-963.
[5] 张宏鑫, 王国瑾. 保持几何连续性的曲线形状调配[J]. 高校应用数学学报: A辑, 2001, 16(2): 187-194.
[6] 刘华勇, 段小娟, 张大明, 等. 基于三角Bézier-like的过渡曲线构造[J]. 浙江大学学报: 理学版, 2013, 40(1): 42-46.
[7] 刘华勇, 张大明, 李璐. 基于参数连续HC Bézier-like曲线的过渡曲线的构造[J]. 纯粹数学与应用数学, 2011, 27(1): 69-74.
[8] 刘华勇, 李璐, 王焕宝. Bézier-like曲线的形状调配[J]. 扬州大学学报: 自然科学版, 2012, 15(1): 65-68.
[9] 刘华勇, 王焕宝, 李璐, 等. 几何连续的Bézier-like曲线的形状调配[J]. 山东大学学报: 理学版, 2012, 47(3): 51-55.
[10] 李凌丰, 谭建荣, 赵海霞. 基于Metaball的过渡曲 线[J]. 中国机械工程, 2005, 16(6): 483-486.
[11] 严兰兰, 梁炯丰, 黄涛. 带形状参数的Bézier曲线[J]. 合肥工业大学学报: 自然科学版, 2009, 32(11): 1783-1788.
[12] 李军成, 宋来忠, 刘成志. 带参数的多项式调配函数与构造基于Metaball的过渡曲线[J]. 中国图象图形学报, 2016, 21(7): 893-900.
[13] FARIN G. Curves and surfaces for CAGD [M]. 5nd ed. San Francisco: Morgan Kaufmann Publishers, 2002: 66.
Design of Transition Curve with Parameters in Shape Blending
YAN Lan-lan1, FAN Ji-qiu1, MA Li2
(1. College of Science, East China University of Technology, Nanchang Jiangxi 330013, China; 2. The First Secondary School in Macheng City Hubei Province, Macheng Hubei 438300, China)
curve design; transition curve; shape blending; shape adjustment
TP 391.72
10.11996/JG.j.2095-302X.2019020379
A
2095-302X(2019)02-0379-09
2018-03-15;
2018-04-30
国家自然科学基金项目(11261003,11761008);江西省自然科学基金项目(20161BAB211028);江西省教育厅科技项目(GJJ160558)
严兰兰(1982-),女,湖北浠水人,副教授,博士,硕士生导师。主要研究方向为计算机辅助几何设计。E-mail:yxh821011@aliyun.com

