一种改进的基于微分方程的曲面求交跟踪算法

史永丰，程 婷，张育浩，徐保文，林岗山



一种改进的基于微分方程的曲面求交跟踪算法

史永丰，程 婷，张育浩，徐保文，林岗山

(金航数码科技有限责任公司，北京 100028)

参数曲面求交是计算机辅助几何设计领域中的关键技术之一。针对传统跟踪算法中曲面求交的漏交和法向共线点处难于处理的问题，提出一种改进的基于微分方程的跟踪算法。首先选择边界点和拐点作为跟踪的起点，解决了漏交问题。并采用基于交线微分形式的跟踪公式计算后继交点，解决了法向共线点处难于处理的问题。最后利用牛顿迭代得到精确交点。该算法不仅正确地跟踪到交线的每个分支，而且易于处理法向共线点处的跟踪，不遗漏关键点，解决了传统跟踪法在法向共线点处交线不连续的问题。与传统跟踪法对比，其鲁棒性和稳定性更强，精度更高且收敛略快，适用于求解任意参数曲面求交问题。

曲面求交；跟踪法；微分方程；法向共线点

参数曲面求交是CAGD/CAM中关键技术之一，被广泛应用于曲面造型(如剪裁[1]、过渡[2])、实体造型(如布尔运算)[3]、制造仿真[4]、人工智能[5]等多个领域中。

常见的求交方法主要有5种：代数法[6]、网格离散法[7-9]、分割法[10-11]、迭代法[12]以及跟踪法[13-14]。跟踪法[15-16]需从事先求出的初始交点出发，根据交线的局部几何关系相继跟踪下一个交点，最后把追踪得到的所有点按序连接起来，从而求出交线。该方法适用范围广、精度高，较为稳定，适用于任意参数曲面求交。

然而传统跟踪法也有一定的缺点，主要表现为：

(1) 尚无有效的方法求得所有交线环的初始点，容易漏交。

(2) 难以确定法向共线点处的跟踪方向，产生的交线带有间断点，不能得到连续完整的交线[17]。

(3) 边界处难于处理，收敛速度慢，不稳定。

鉴于此，本文对上述问题作进一步研究，首先选择边界点和拐点作为跟踪的起点，然后利用交线的微分形式将跟踪点投影到参数域中计算后继交点，最后利用牛顿迭代得到精确交点。

1 基于微分方程的跟踪算法原理

传统的参数曲面跟踪求交，需要先用分割法或网格法求得交线的拓扑结构和交点的估计值作为跟踪起点。因此，分析交线的拓扑结构并选择恰当的初始点成为跟踪算法首要解决的问题。

1.1 确定跟踪起点

曲面交线有两种常见的拓扑结构：交线段和闭环。而交线段和闭环上还可能存在法向共线点，两曲面在该点处的法向量是共向的，无法确定在该点处的跟踪方向。另外，当跟踪到这些法向共线点附近时，还可能存在不同分支距离很近的情况，此时若跟踪步长过大容易出现跟踪偏离或者循环。为了避免上述情况，本文通过拓扑分析找到其法向共线点，当跟踪到这些点附近时，减小步长，避免偏离和循环的发生，并通过本文的跟踪过程(2.2节)计算在法向共线点处的跟踪方向，继续跟踪。

1.1.1 法向共线点和拐点

对于两参数曲面(,)与(,)的求交。由上文可知，法向共线点在跟踪过程中扮演很重要的角色，需要求出该2曲面所有的法向共线点。由文献[17]，求解法向共线点等价于求解如下非线性方程组

为了正确地跟踪交线上的所有闭环，需找到每一闭环上的一个点作为跟踪起点。文献[15]中已证明只要找到拐点或拐点，即可开始跟踪闭环。先给出拐点的定义。

1.1.2 交线的拓扑分析

为了确保跟踪正确，有2个关键点：

(1) 跟踪起点为中的元素。

(2) 每一步跟踪时，都要检查当前点是否在法向共线点附近。若在，则减小跟踪步长，防止跟踪的偏离或循环的发生。若当前点就是法向共线点，则计算法向共线点处的跟踪方向，继续跟踪。

1.2 跟踪交线

1.2.1 交线的微分形式

设两参数曲面分别为(,)与(,)，并假设,至少是1的，则求该2曲面的交线，即

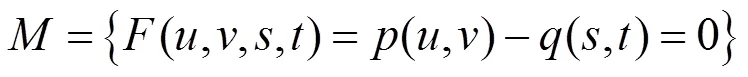
也就是说，当交点集合非空，2曲面相交，且集合包含1条或几条交线段，对于任意的参数每一条交线段均满足条件

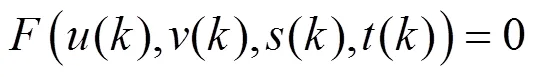
其为交线的空间曲线方程。在2个参数域上的投影分别为两平面曲线。

曲面和在交线上的一点(,,,)处的单位法矢分别为

由微分几何中交线上一点的法矢与切矢垂直可得

而由式(3)与式(4)可直接得到的微分

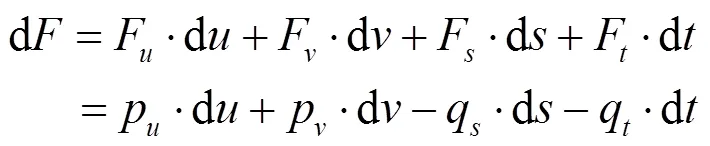
将式(7)代入式(6)可得方程组

求解上述方程组可得

其中，D1，D2为常数。若令

式(9)与式(11)都为交线式(3)的微分形式。

1.2.2 确定后继交点

传统的跟踪法确定下一个交点的过程，通常是在给定起点后，沿着交线的切矢方向前进一定的步长，跟踪需在点的三维空间中进行，想要获得点的参数坐标还需要通过牛顿迭代，并且无法确定在法向共线点处的跟踪方向。

另外，文献[15]说明了由于式(9)与(11)有两个常数D1，D2，因此在确定跟踪公式(12)中的步长时，有一定的自由度。其既能保证Euler方法是收敛的，又使交线的参数分布均匀。

1.2.3 算法关键点

上文已经比较详细地说明了跟踪算法的全过程，但在实际应用中，仍需要有几点值得注意：

令()=(,,,)=(,,,)·n(,)，将(+d)在处二阶泰勒展开得到关于的一元二次方程

其中，=p·n，=p·n，=p·n，=–2，求解上述方程得

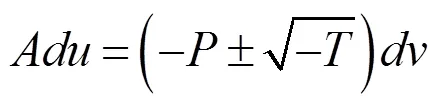
对分0；=0；0 3种情况讨论，可确定法向共线点的类型及跟踪方向[10]，解决了传统跟踪算法在法向共线点处难于处理的问题。

(2) 利用式(12)迭代地计算后继交点的终止条件为：①(,)和(,)中任意一个的参数值超出其定义域；②跟踪到起点(包括边界点和拐点)。

(3) 本文选择4参数迭代法[14]作为得到精确交点的方法，并规定迭代的最大次数及算法终止的精度阈值。事实上，在2.1节的数值实验中，一般只需要2~4次迭代即可达到精度要求。

(4) 针对跟踪过程可能会出现跟踪起点的冗余问题，即跟踪得到的某条交线可能通过跟踪起点集合里的某几个点，需对跟踪起点集合进行检查，删去该交线已经通过的跟踪起点，避免对同一条交线重复计算。本文规定一个最小距离标准，即删除与交线间距离小于给定的最小距离的点。

2 数值实验

本文数值实验根据微分方程的跟踪算法进行测试，来说明算法的处理能力。算法的控制参数如下：4参数迭代法的精度阈值=10–6，控制迭代的最大次数为10 000。对于传统的跟踪法，其跟踪起点为利用网格法求交得到的交点。本算法适用于任何光滑曲面(片)，这里选取Bézier曲面进行测试。若要选取NURBS曲面，可以根据文献[19]转化为Bézier曲面。

2.1 实验用例

充分考虑2曲面间交线的情况。交线分为2种：交线段和闭环。交线段包括只有边界点，无拐点交线段、有边界点及拐点的交线段。闭环选取有法向共线点和拐点的环，共3个实验来测试本文算法。

2.1.1 有边界点、无拐点的交线段

2个3×2次Bézier曲面相交形成如图1所示的只有边界点，无拐点的交线段。

两曲面的控制顶点如下

该交线2边界点的参数分别为(,,,)= (0.0286, 0.0968, 0.0325, 0.0973)和(,,,)= (0.9958, 0.9549, 0.7377, 0.9550)。

2.1.2 有边界点和拐点的交线段

2曲面的表达式分别为

图2为上述两曲面的交线及对应的参数域。该交线为含有2个边界点和1个u拐点的交线段，交线两边界点的参数分别为(u, v, s, t)=(0.0008, 9.5125, 0.0183, 9.5116)和(u, v, s, t)=(9.5116, 0.0183, 9.5125, 0.0008), 在(u, v)=(9.5081, 0.0814)处交线存在u拐点。

2.1.3 有法向共线点和拐点的闭环

为了验证本文算法能否正确完整地跟踪含有闭环结构的交线，还需考虑了2曲面间的交线为含有法向共线点和拐点的闭环。

2曲面的表达式分别为

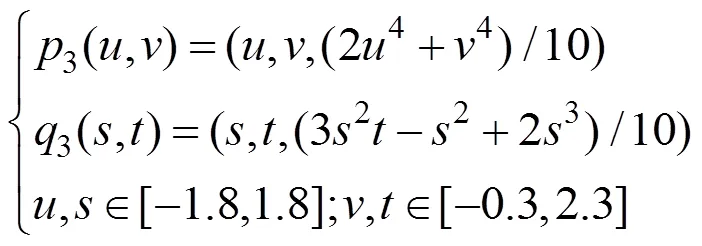
图3为利用本文算法与传统的跟踪算法计算得到的上述2曲面交线及其对应的参数域。利用本文算法计算得到，在−参数域上，交线在点(,)=(0.2084, 0.2566)和(,)=(1.5250, 1.3645)处存在法向共线点，在点(,)=(1.5608, 1.2223)，(,)=(0.1956, 0.2902)存在拐点，并且可以获得完整的不存在间断点的闭环。

最后，验证了对于任意含有法向共线点的闭环，通过微分形式的曲面求交跟踪算法，均可以得到完整的闭环，2求交曲面的表达式为

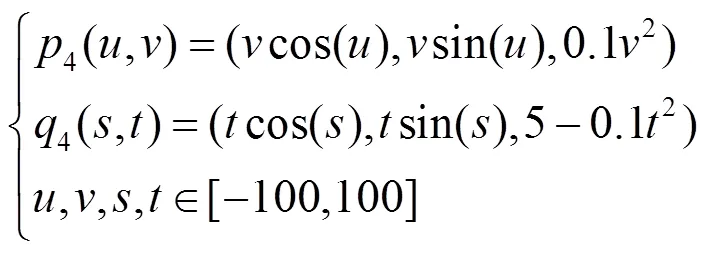
求交得出的完整闭环如图4所示。

图4 含有法向共线点的闭环验证

2.2 性能分析

对于曲面求交算法的鲁棒性，表现在2个方面：①不遗漏关键点；②保证求得的结果与实际交线拓扑一致。由上文可知，利用本文算法在以上3个实验中进行测试均能计算出与实际交线拓扑一致的交线，并且没有遗漏法向共线点和拐点这样的关键点，交线完整且连续。然而在利用传统跟踪法计算含有法向共线点和拐点的闭环交线时，由图3看出，闭环交线在2个法向共线点处存在间断点。同时，由于传统跟踪法无法处理法向共线点处的精确求解问题，因此在法向共线点(,)=(−0.0010, 0.0729)处，传统跟踪法在其附近的跟踪过程表现出明显的数值不稳定性，该点与利用式(1)精确计算得到的法向共线点有些偏离，从而计算出的交线与实际交线有所偏差。上述事实也验证了本文算法在经过精确的拓扑分析以及有效的跟踪过程后具有一定的稳定性和鲁棒性。

最后，验证算法的跟踪效率，将算法跟踪过程的时间和得到的交点数作为验证算法跟踪效率的比较指标。时间取50次跟踪交线过程所需时间的平均值。表1和表2为上述3个实例下2种算法跟踪效率的比较结果。

表1 传统跟踪法的实验数据

表2 本文算法的实验数据

由表1和表2可知，对于上述3个实例，利用本文算法计算得到的交点数略多于传统跟踪法，而计算时间却比传统跟踪法要少，说明不论是交线段还是闭环，本文算法每计算1个交点所用时间更少，也就是说其跟踪过程能够更快的收敛，克服了传统跟踪法在边界和法向共线点附近收敛慢，不稳定的缺点。综上，本文算法有效地兼顾了鲁棒性和效率2个方面。

3 结论与讨论

鉴于曲面求交难于处理的漏交和法向共线点处的跟踪问题，本文提出一种改进的基于微分方程的跟踪算法。该算法选择边界点和拐点作为跟踪的起点，解决了传统跟踪算法的漏交问题，并采用基于交线微分形式的跟踪公式计算后继交点，解决了传统跟踪算法在法向共线点处难于处理的问题，最后利用牛顿迭代得到精确交点。该算法不仅正确地跟踪到交线的每个分支，而且易于处理法向共线点处的跟踪，不遗漏关键点，能产生完整连续的交线。与传统跟踪法相比，鲁棒和稳定性更强，精度更高且收敛略快，适用于求解任意参数曲面求交问题。若初始点不在边界、拐点处，有可能导致求交失败。有效选取初始点仍是跟踪问题难点之一，有待进一步研究。

[1] 伯彭波, 袁野, 张彩明. 可展曲面的自动识别与重建[J].计算机辅助设计与图形学学报, 2016, 28(9): 1428-1435.

[2] 马翔, 康宝生, 周儒荣. 一种用NURBS表示的过渡曲面的生成方法[J]. 航空学报, 1992, 13(12): 678-681.

[3] 周建华, 琚建军, 范玉青. 高效可靠的实体造型隐藏线删除算法[J]. 工程图学学报, 1993, 14(2): 54-62.

[4] 李丹, 良辰. 高制造与仿真[J].航空制造技术, 2017, 2017(4): 32-33.

[5] 葛文武, 韩江洪, 魏臻, 等. 最小最大车辆路径问题的动态自适应蚁群优化算法[J]. 模式识别与人工智能, 2015, 28(10):930-938.

[6] PRATT M J, GEISOW A D. Surface/surface Intersection Problems. The Mathematics of Surface [M]. Oxford: Oxford University Press, 1986: 117-142.

[7] 李宁, 田震, 张立华, 等. 优化的三角网格曲面求交算法[J]. 辽宁工程技术大学学报: 自然科学版, 2013, 32(9): 1269-1273.

[8] 蒋钱平, 唐杰, 袁春风. 基于平均单元格的三角网格曲面快速求交算法[J]. 计算机工程, 2008, 34(21): 172-174.

[9] 花卫华, 邓伟萍, 刘修国, 等. 一种改进的不规则三角网格曲面切割算法[J]. 中国地质大学报, 2006, 31(5): 619-623.

[10] HONGHTON E G, EMENTT R F, FACTOR J D. Implementation of a divide-and-conquer method for intersection of parametric surfaces [J]. Computer Aided Geometric Design, 1985, 2(1-3): 173-183.

[11] 席平. 任意参数曲面的分割求交算法[J]. 北京航空航天大学学报, 1984, 3: 71-80.

[12] BARTH W, LIEGER R, SCHINDLER M. Ray tracing general parametric surfaces using interval arithmetic [J]. Visual Computer, 1994, 10(7): 363-371.

[13] BARNHILL R E, KERSEY S N. A marching method for parametric surface/surface intersection [J]. Computer Aided Geometric Design, 1990, 7(1-4): 257-280.

[14] 许晓革, 冀阳峰, 杨蕾. 曲面离散跟踪求交算法的研究[J]. 工程图学学报, 2005, 26(1): 61-64.

[15] 黄金贵, 康宝生. 任意曲面间跟踪求交的有效算法[J]. 计算机辅助设计与图形学学报, 1998, 10(6): 499-505.

[16] 杨宝光. 一种高效可靠的多项式参数曲面求交算法[D]. 杭州: 浙江大学, 2006.

[17] SHERBROOKE E C, PATRIKALAKIS N M. Computation of the solutions of nonlinear polynomial systems [J]. Computer Aided Geometric Design, 1993, 10(5): 379-405.

[18] 朱心雄. 自由曲线曲面造型技术[M]. 北京: 科学出版社, 2000: 1-391.

[19] SHEN J J, BUSÉ L, ALLIEZ P, et al. A line/trimmed NURBS surface intersection algorithm using matrix representations [J]. Computer Aided Geometric Design, 2016, 48: 1-16.

An Improved Algorithm for Tracing Surface Intersection Based on Differential Equation

SHI Yong-feng, CHENG Ting, ZHANG Yu-hao, XU Bao-wen, LIN Gang-shan

(Jinhang Digital Technology co. LTD, Beijing 100028, China)

Intersection of parametric surfaces is one of the key technologies in the field of computer aided geometric design (CAGD). In this paper, an improved tracing algorithm based on differential equation is proposed to solve the problem in traditional tracing algorithm of missing intersection line and difficulty to trace at normal collinear points. Firstly, the algorithm chooses the boundary points and the inflection points as the starting points of the tracing, so it solves the problem of missing intersection line. Then the tracing formula based on the differential form is used to calculate the successor intersection, which solves the problem of processing tracing at normal collinear points. Finally, the Newton iteration is used to get the exact intersection. The algorithm not only correctly traces each branch of the intersection line, but also is easy to deal with the tracing at normal collinear points. Without missing the key points, the algorithm solves the problem that the traditional tracing method is not continuous at the normal collinear points. Compared with the traditional tracing method, its robustness and stability are stronger characterized with higher precision and slightly faster convergence, and it is suitable for solving any parametric surface intersection problem.

surface intersection; tracing method; differential equation; normal collinear points

TP 391.41

10.11996/JG.j.2095-302X.2019020290

A

2095-302X(2019)02-0290-06

2018-08-30；

2018-09-11

史永丰(1980-)，男，湖南郴州人，高级工程师，硕士。主要研究方向为CAD、计算机图形学。E-mail：shiyf@avic-digital.com

程 婷(1988-)，女，山西晋中人，工程师，博士。主要研究方向为CAGD、CAD、计算机图形学。E-mail：chengt@avic-digital.com