基于改进SDAE算法的复杂系统故障识别
史永胜,衡慧娟
(中国民航大学航空工程学院,天津 300300)
传统的数学建模方式对复杂系统的故障识别较困难。杜玮等[1]提出基于改进BP神经网络的复杂系统故障识别方法,利用变学习速率法与共轭梯度法相结合的BP网络性能改进算法,将其用于复杂系统的故障识别。贾文其等[2]基于栈式降噪自编码神经网络对车牌字符进行识别,在复杂环境下低质量的车牌字符图像识别具有较好的鲁棒性。丁平等[3]采用径向基函数(RBF)神经网络建立发动机的故障识别模型,论述了径向基函数神经网络的结构、学习和运行,并通过该模型对发动机参数进行辨识,具有较高的故障识别率。Cho[4]提出简单稀疏化方法,从而增强稀疏去噪自编码网络去除图像噪声的高效性,且实验验证了稀疏性有助于小图像碎片和含较多碎片的较大图像的去噪。袁静等[5]提出融合梯度差信息的稀疏去噪自编码网络在异常行为检测中的应用,在稀疏去噪自编码的基础上,增加梯度差的约束条件,改进了自编码网络的解码效果。
复杂系统的故障种类多样,成因错综复杂,针对已有基于稀疏去噪编码网络(SDAE,sparse denoising autoencoder)算法在复杂系统故障识别中的故障识别率低、重构误差较明显、算法参数过多及训练过程缓慢等问题,在传统的SDAE算法中引入数据量化和故障码匹配的概念,使改进后的SDAE算法具有故障识别效率高和噪声样本数据鲁棒性强等优点。
1 稀疏去噪自编码网络
自编码网络(AE,autoencoder)自Hinton等学者在2006年首次提出后,引起学术界的广泛关注。AE是一种无监督的特征学习网络,可充分利用未标签数据通过逐层的预训练得到各层网络初始化的权值,从而使网络能更有效地提取数据特征。
AE由三层网络组成,分别是输入层、隐含层和输出层。AE要经过编码、解码阶段,编码阶段是从输入层到隐含层的压缩低维表达过程,解码阶段是从隐含层的压缩特征映射还原出输出层的近似原始数据的过程。
当原始的输入数据包含噪声时,自编码网络的性能将会降低,为避免这一现象的发生,Vicent等提出去噪自编码网络(DAE,denoising autoencoder)的概念。先对原始的输入数据添加随机噪声,然后对加噪后的数据进行编码、解码操作,最终的输出数据能够近似等于原始的输入数据[6]。
如果将稀疏性引入到自编码网络中可得到另一种稀疏自编码网络(SDAE),该网络限制每次获得的编码尽量稀疏,从而模拟人脑中神经元刺激和抑制的规律,稀疏自编码网络的优化模型如下

其中:h=WTX为编码后的信号;X为输入数据;W为层间的连接权值矩阵;hj为第j次编码后的信号;l为其权重系数;L(X,W)为稀疏自编码网络的优化函数。通过式(1)中的第2项可约束编码信号足够稀疏,获得对原始信号更加紧凑简洁的表示。
对DAE的隐含层增加稀疏约束条件[7],当隐含层神经元数大于输入数据时,自编码网络能发现输入数据的结构特征。
设X为神经网络的输入,加入稀疏约束ρ(可根据实验经验设为0.2),并在优化目标函数中增加额外的惩罚因子,即

其中:j为神经网络中的隐含层神经单元号;n为隐含层的层数;j为第 j个隐含层的平均激活值el为第j层神经网络的第l个响应值;k为第j个隐含层的神经元的个数,则损失函数为
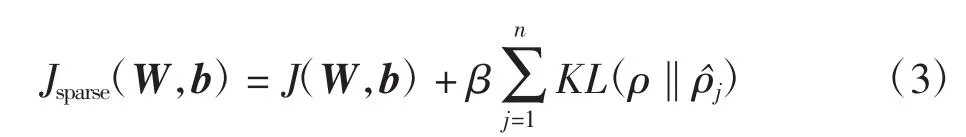
其中:β为控制稀疏性惩罚因子的权重;b为神经元Bias值向量。式(3)中第2项称为稀疏正则项,可使训练时隐含层输出趋于0,从而得到具有稀疏表示的检测特征。
2 改进稀疏去噪自编码网络
2.1 核心思想
在传统SDAE算法的基础上,引入数据量化和故障码匹配的思想。改进SDAE算法的核心思想是在隐含层添加稀疏性限制后,提取输入数据的相关特征参数向量,在此基础上对相关参数数据进行量化,经过细化后再用故障码匹配法进行匹配,然后再次输出。传统SDAE算法是学习一个恒等函数,最终的输出数据和输入数据基本相近;改进SDAE算法在此基础上最终是以0和1的形式输出,能更好地提高复杂系统故障识别度。
2.2 结构表示
改进的 SDAE 结构如图 3 所示,其中:X=(x1,x2,…,xn)为输入的原始数据;Y=(y1,y2,…,ym)为加入稀疏限制得到的特征参数数据;Z=(z1,z2,…,zn)为输出数据。
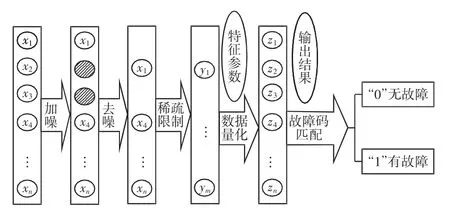
图1 改进SDAE结构图Fig.1 Improved SDAE structure
在原始输入数据X中加入随机噪声,经过去噪处理获得较纯净的输入数据;经过大量训练后得到比较适合的稀疏性参数ρ,在隐含层上加入适合的稀疏性限制,从而获取输入数据的特征参数数据;特征参数数据经过特殊的0-1数据量化后与样本进行比较,根据比较结果再利用故障码匹配方法进行匹配,从而输出0-1编码结果。在数据的重构方面都会存在一定的误差,其中,数据重构误差平方和作为一个很重要的量化指标,其表达式为

其中:xi为第i个输入数据,zi为第i个输出数据。
2.3 引入思想
2.3.1 特征参数数据量化
该方法是将原始数据经过自编码网络一系列的处理后,得到去噪后数据的特征参数Y,然后和故障样本数据的特征参数 L 进行比较,L=(l1,l2,…,lm),li为第i个故障样本数据的特征参数数据。yi与li不同时为0,相同时为1。最终输出与输入神经元数量相等,可以更小的误差来重构输出层,输出层由0-1编码的形式输出。
令 P=(p1,p2,…,pm),pi=yi⊙li,P 为量化后的数据,由一系列0-1编码表示。
特殊情况下,即输出全为0的情况下,为了进一步精确,需要进行二次量化。令Δpi=yi-li,Δpi为输入数据经处理后的第i个特征参数和故障样本数据集中第 i个特征参数之间的误差值。如果 yi>li,Δpi∈的情况下,则有故障,如果yi<li,也存在故障,量化结果均显示为1;其他量化结果显示为0。
2.3.2 输出层故障码匹配
将输出层Z的0-1编码与故障样本的编码数据以映射的方式1-1对应进行匹配,若匹配成功则有故障,反之无故障。
令故障样本数据的编码数据 M=(m1,m2,…,mn)。
如果zi⊙mi=0,表示输出数据编码与故障样本数据编码不同,则原始输入数据没问题,无故障发生;如果zi⊙mi=1,表示输出数据编码与故障样本数据编码相同,则原始输入数据有问题,有故障发生。
根据以上规则,且经过反复推算验证可得出

其中:n一般取小于14的正整数;t为编码数值范围。根据已有样本数据,t∈[0,10 000],表示和故障码匹配结果可行,在正常情况下,此式比较适用,正确率很高,但式(5)有一定缺陷,依赖于样本数据,对于新型的故障样本数据,缺乏一定的准确率。
2.4 计算过程
第1步首先向原始输入数据中加入随机噪声(使原始的输入数据在某些维度上值为0);然后将加入噪声的数据输入网络,经过编码,如果隐含层神经元数量大于输入层神经元数量,在隐含层加入稀疏性限制,发现输入数据的相关结构特征,从而得到输入数据的特征参数数据。
第2步采用数据量化方法对输入数据的特征参数进行0-1量化,从而得到P,然后重构出输出层Z。如果输入输出的误差函数值过大,则重复第1步和第2步,使误差值控制在一个可接受的范围内。
第3步用故障码匹配方法把输出层Z的编码序列与故障样本数据的编码序列进行智能化匹配,从而找出哪些数据中存在故障现象。
3 结果分析
为说明该方法的有效性,选择某型航空发动机轴承系统作为研究对象,同时选取两个案例进行分析。
案例1数据取自文献[8-9]中的航空发动机轴承故障数据。根据2.3.1节方法,数据量化结果以编码形式输出,根据数据量化条件设置参数ρ=0.05,从两组数据编码结果中各选取10个量化结果,如表1所示。
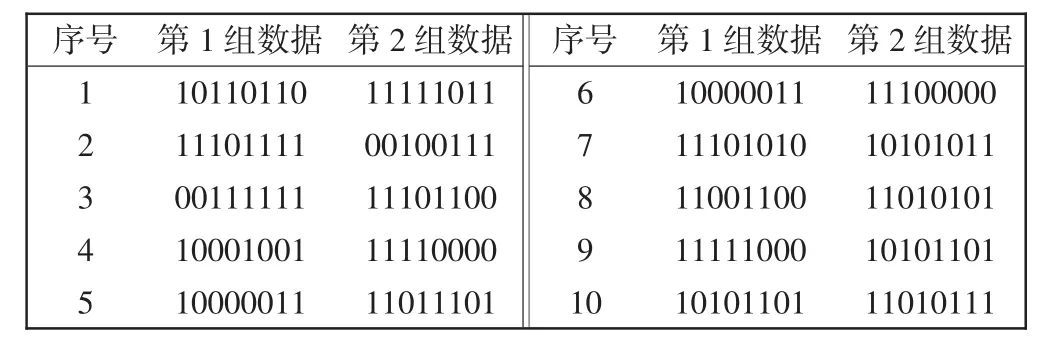
表1 数据量化结果Tab.1 Quantified data
用Matlab对两组数据进行仿真,主要从重构误差和故障识别率两个方面进行分析。由图2可看出,改进SDAE算法的重构误差比传统SDAE算法小。由表2可看出,改进算法的重构误差平均降低1.5%。

图2 传统与改进SDAE算法重构误差Fig.2 Reconstruction error comparison between traditional and improved SDAE algorithms

表2 传统与改进SDAE算法的重构误差Tab.2 Reconstruction error comparison between traditional and improved SDAE algorithms
图3为SDAE算法故障识别率随样本数的变化。开始时故障识别率随着样本数的增加而增大,样本数大概达到7×104时,识别率达到最大,之后随着样本数的增大,识别率趋于平稳。传统SDAE算法故障识别率大致变化规律和改进SDAE相同,但整体处在实线的下方,因此,改进SDAE算法的故障识别率更高。两组数据验证结果表明,改进SDAE算法的故障识别率平均提高9%。
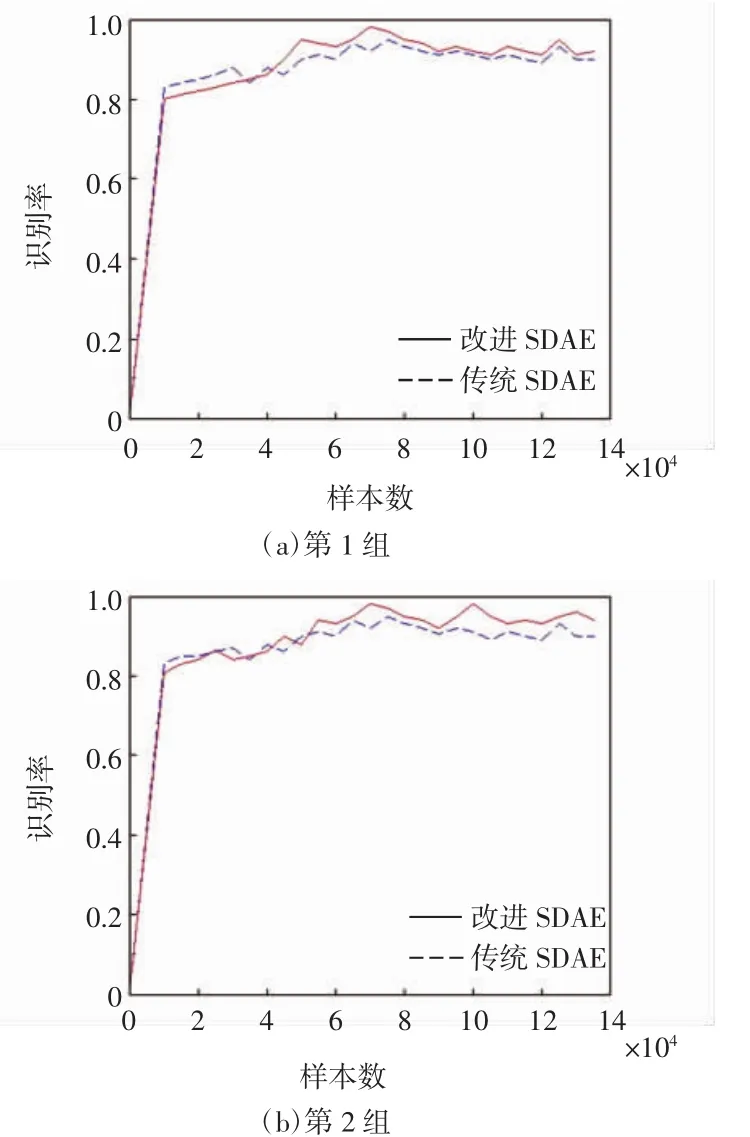
图3 传统与改进SDAE算法故障识别率Fig.3 Failure recognition rate comparison between traditional and improved SDAE algorithms
案例2 数据引自文献[10],此案例主要分析去噪自编码网络、深度降噪自编码(DDAE)、传统SDAE算法、改进SDAE算法的重构效果。本案例对这几种自编码网络采用5层的网络结构进行分析,把重构误差平方和作为数据重构的定量评价指标。
DAE、DDAE、传统 SDAE、改进 SDAE 4种自编码网络的重构误差平方和,如表3所示。
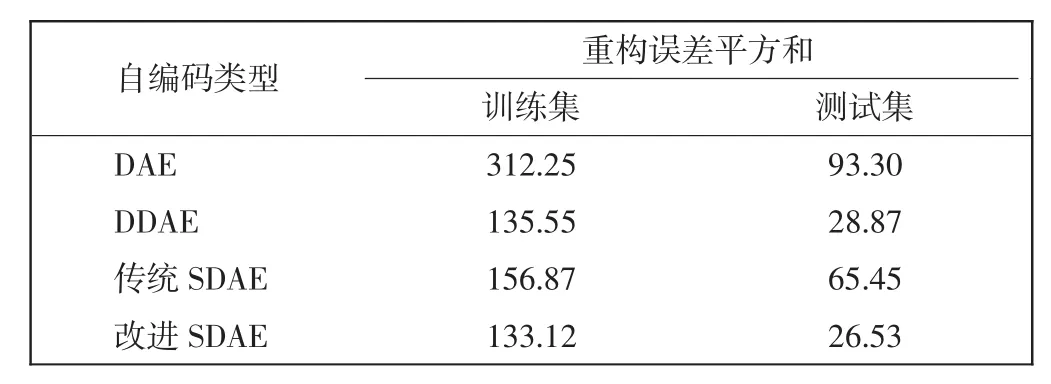
表3 各种自编码网络重构误差平方和Tab.3 Reconstruction error quadratic sum of various self-coded networks
经过对比发现,在以上几种自编码网络算法中,改进SDAE在训练集和测试集上的重构误差平方和均取得最小值,说明改进SDAE的隐含层特征提取效果最好。
4 结语
在传统SDAE算法的基础上,引入了数据量化和故障码匹配的思想,有效降低了输入输出的误差函数值,提高了复杂系统故障识别精度。不足之处是该方法过于依赖故障样本数据,对一些新型的故障类型难以做到及时识别,因此该方法的应用范围受到一定的限制,但同时也是进一步的研究方向。
——以某铅锌矿为例

