基于热力模型的发动机单元体性能研究
曹惠玲,刘乃彬,薛 鹏,于天浩
(中国民航大学a.航空工程学院;b.工程技术训练中心,天津 300300)
航空发动机单元体性能与整机性能之间有很大联系,其工作状态的好坏直接影响到飞机的可靠运行以及机组成员和乘客的生命安全,因此,准确分析单元体性能及其与整机性能的关系十分重要,可为发动机维修和故障诊断提供指导。由于发动机的部件特性和控制规律很难获得,目前主要集中在通过实际QAR数据和试车台数据进行拟合,建立各单元体效率与流量对发动机排气温度偏差值和燃油流量偏差值的贡献率模型,确定单元体性能对整机性能的影响关系。唐海龙等[1]应用蒙特卡洛概率设计方法建立涡轴发动机部件机非确定性非线性性能模型,利用发动机各部件效率和流量,研究某工况下各部件性能的非确定性对发动机性能的影响。赵琳等[2]通过辨识建模的方法先建立稳态模型,在其基础上又建立动态模型,对发动机多组试车数据进行辨识检验,研究发动机全包线、全工况的实时性能参数变化。航空发动机是一个非常复杂的热力机械系统,各单元体工作过程不同,但彼此有大量联系,其工作过程可用相应的热力方程表示,但方程存在强烈的非线性,要获得发动机性能数据,需要大量的迭代计算求解[3]。因此需要从发动机原理出发,结合实际QAR数据,将非线性方程转化为线性方程,去除迭代计算,建立反映单元体性能与整机性能关系的数学模型。Urban[4-5]于20世纪60年代提出了一种线性模型气路分析法,应用小偏差理论研究燃气轮机故障,为发动机非线性的气动热力方程转化为线性方程提供了依据。
根据发动机工作原理以及各单元体的热力方程,应用小偏差理论,建立了各单元体的小偏差模型。又根据各单元体间的流量平衡关系和压比平衡,结合上述各单元体模型,建立了发动机部件性能和整机性能参数关系的数学模型。通过此模型研究部件特性与整机性能之间的关系。
1 小偏差数学理论基础
小偏差法是一种近似计算方法,通过自变量发生的微小变化确定因变量的相应变化量[6]。设发动机系统的热力参数之间存在以下函数关系

其中:x为性能参数;y为可测参数(用于部件性能参数对整机参数的求解结果)。在基值(x10,x20,…,xm0)领域内存在n+1阶的连续偏导数,则函数y可在基值领域内按泰勒级数[7-8]展开,即

忽略上式右边的二次项及以后各项,简化得
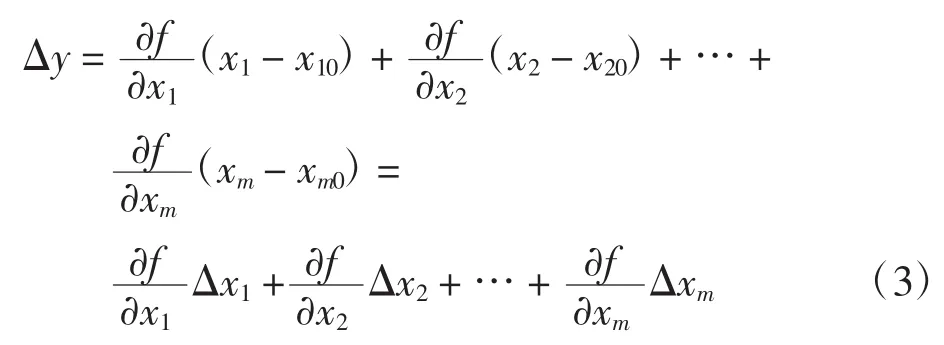
上式表示性能参数偏差和可测参数偏差之间的线性关系方程,且各参数之间保持原有的量纲单位,为简化计算,减少不同量纲之间的影响,用式(3)等号两端分别除以式(1)等号两端进行无量纲化处理,得到表达式为

其中:a1,a2,…,am为方程系数为可测参数偏差量;为性能参数偏差量。
2 发动机数学模型建立
2.1 主要部件组成及工作过程
双轴涡扇发动机目前应用较广泛,其主要部件有进气道(Inlet)、风扇(Fan)、低压压气机(LPC)、高压压气机(HPC)、燃烧室(C/C)、低压涡轮(LPT)、高压涡轮(HPT)、尾喷管(Nozzles)。将发动机工作过程理想化,忽略漏气、压气机引气的损失;不考虑外涵道影响,将发动机简化成只有1个涵道,气体的流动为一元流动;尾喷管为不可调收敛性喷管且气体完全膨胀。在此基础上根据部件工作过程建立发动机故障诊断数学模型。发动机具体站位划分如图1所示。
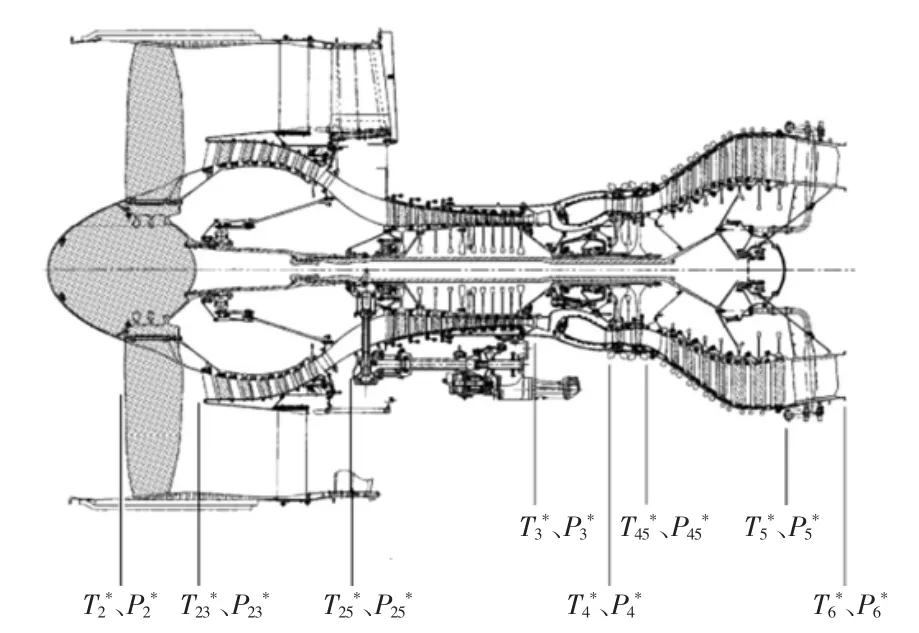
图1 发动机站位图Fig.1 Engine station diagram
2.2 单元体模型建立
应用小偏差理论对发动机各单元体的热力方程进行偏差处理,得到每个单元体的小偏差方程,如式(8)~(19)所示。其中Ki为各偏差方程系数;Ti*和Pi*分别为各单元体的截面参数温度和压力,如图1所示;π为压比,不同单元体的压比分别用不同的下角标表示;N1为低压转速;N2为高压转速。首先,风扇工作过程的热力方程如下。
耗功方程为

效率方程为

其中:T2*为风扇进口温度;T23*为风扇出口温度(低压压气机进口温度)为风扇压比;P2*为进口压力;P23*为风扇出口压力(低压压气机进口压力);γ为空气系数;R为热力学常数。
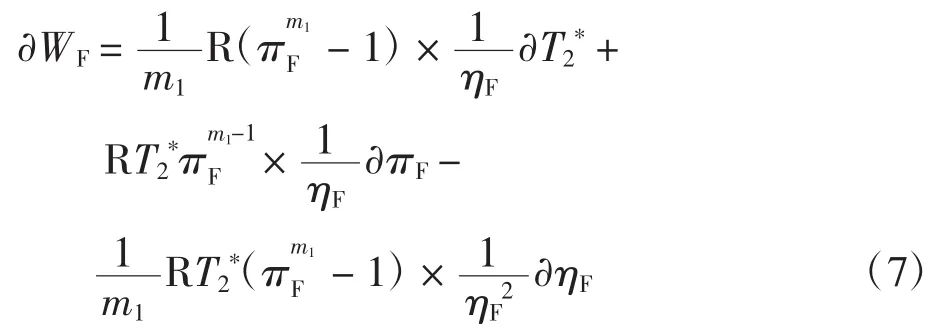
对上式进行无量纲化,得到风扇耗功小偏差方程为
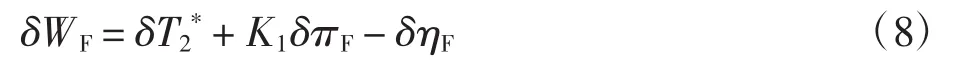
同理,可得效率的小偏差方程为

同理,可得低压压气机小偏差方程为

高压压气机小偏差方程为


低压涡轮小偏差方程为
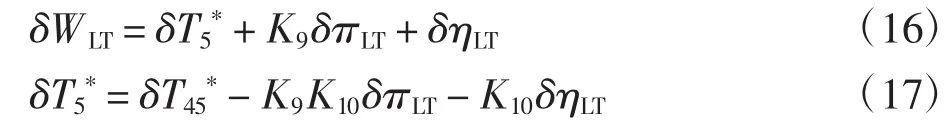
燃烧室燃烧过程能量平衡方程为
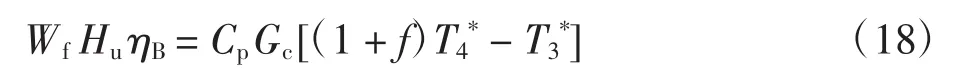
其中:Wf为燃油流量;Hu为燃油低热值;ηB为燃烧效率;Cp为空气定压比热容;Gc为发动机进气量;f为油气比。
对应的小偏差方程为
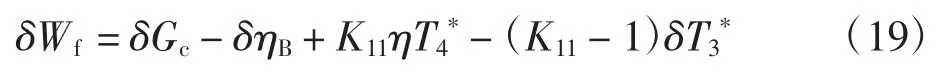
2.3 性能参数变化量分离
航空发动机发生故障时,其单元体性能参数的变化包含两方面:①各单元体的自身故障使其特性发生变化,造成各单元体效率和流量的改变,如图2~图3中的AA1过程,A为发动机发生故障前的工作点,部件故障引起特性线移动到A1,此时流量和效率的变化量为和δηF0;②发生故障后,各单元体要重新匹配达到新的平衡工作点,也会引起效率和流量的改变[9],如图2~图3中,A1A2′过程为发生故障后,部件重新匹配,满足功率与转速平衡的条件,移到了新平衡点A2′。通过单元体通用特性曲线工况点的变化可以确定发生故障时单元体性能参数的独立变化量,排除其他单元体性能参数的影响。
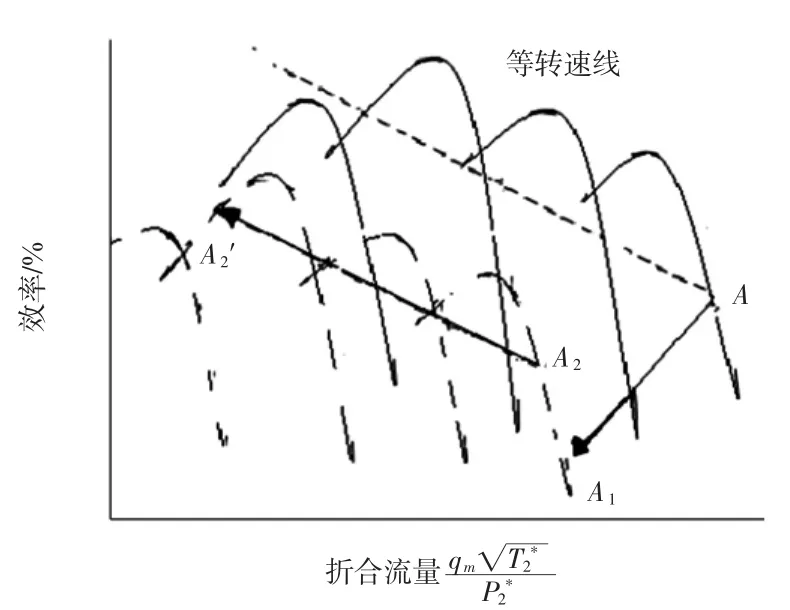
图2 发生故障时折合流量与效率和转速的工况点变化Fig.2 Change of flow rate,efficiency and rotation speed in case of failure

图3 发生故障时折合流量与压比和转速的工况点变化Fig.3 Change of flow rate,pressure ratio and rotation speed in case of failure
将A1A2′过程分为沿新的等转速线上变化的A1A2和沿平衡工作线变化的A2A2′两个过程。其中A1A2过程的流量和效率分别为GA1和ηA1,A2A2′过程的流量和效率为GA2和ηA2。所以由发生故障前的点A到新的平衡工作点A2′,部件的流量和效率变化分别由3部分组成,用小偏差方程表示为
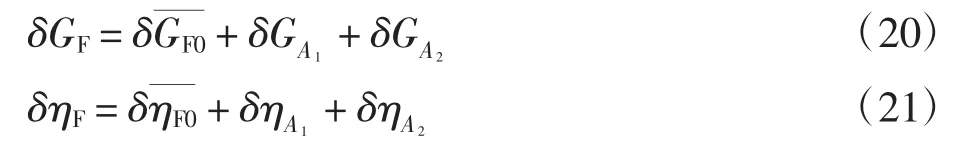
A1A2过程在等转速线上移动,转速不变,流量和效率为关于压比的方程,表示为

对应的小偏差方程为
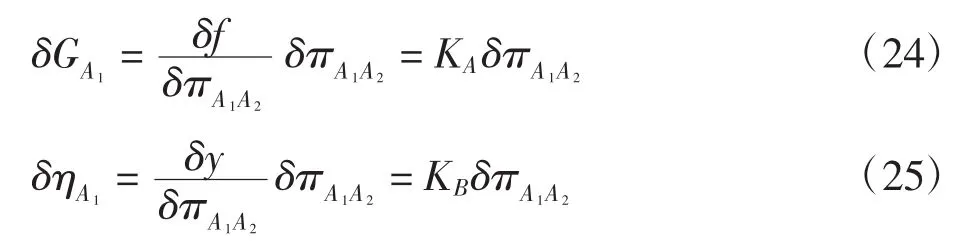
A2A2′过程关于压比的小偏差方程为

又由于此过程转速不断变化,设πA2A2′=φ(nA2A2′),其偏差方程为

将式(28)代入式(26)~(27),有

由于AA1过程为等压比过程,其变化量为0,所以风扇总压比变化量的偏差方程由两部分组成,即

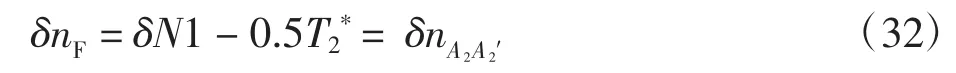
将式(24)、式(29)、式(31)~(32)代入式(20),得到风扇流量的小偏差方程为

同理得:
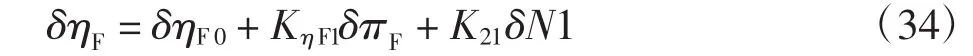
同理可得其余单元体流量和效率的分离偏差方程。将分离的性能参数偏差方程[10]代入2.2节建立的各单元体小偏差方程,得到各单元体偏差方程,如表1所示。
2.4 矩阵模型建立
发动机在工作过程中,各单元体之间存在内在联系。运用双轴燃气轮机中转子功率相等、各单元体间流量平衡、压比平衡等条件,对式(19)、式(35)~(50)进行联立求解。求解流程如图4所示。
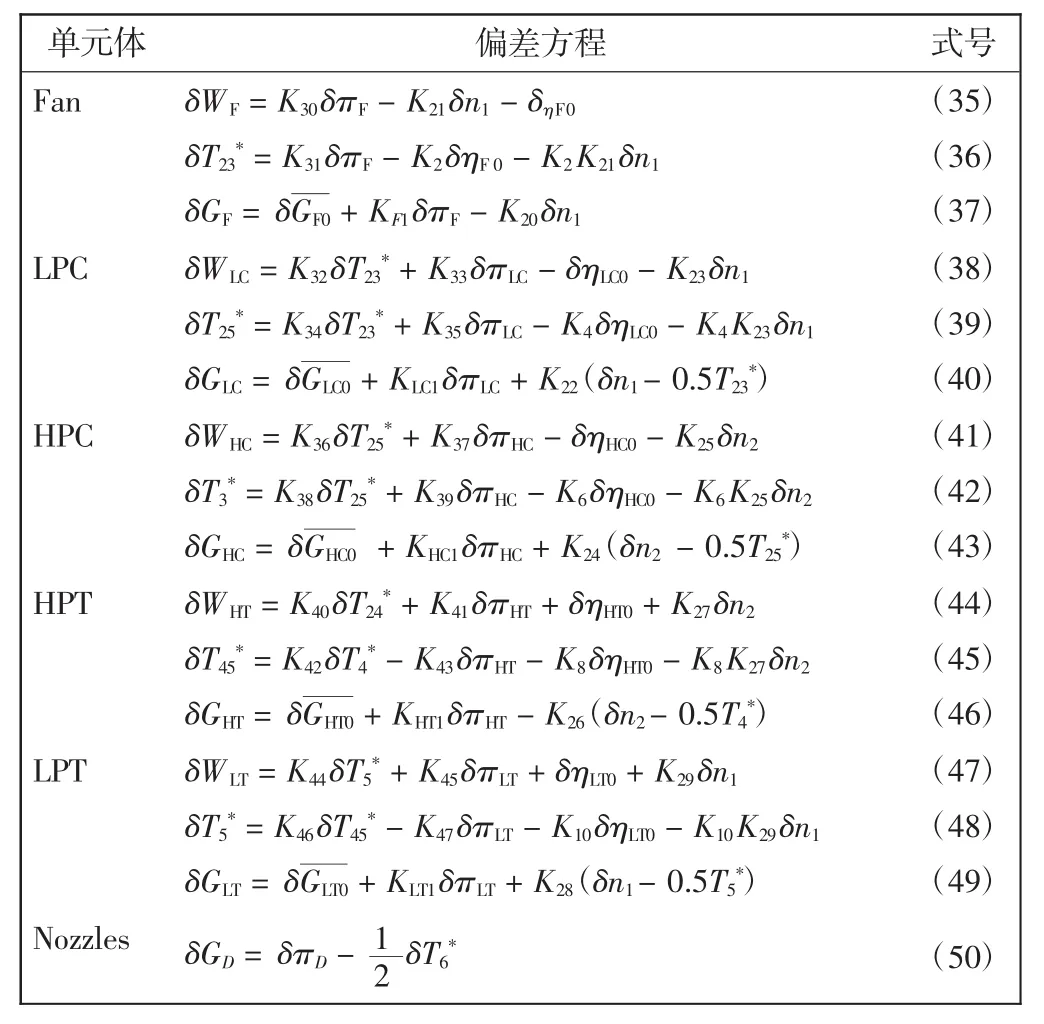
表1 单元体偏差方程Tab.1 Engine unit deviation equation
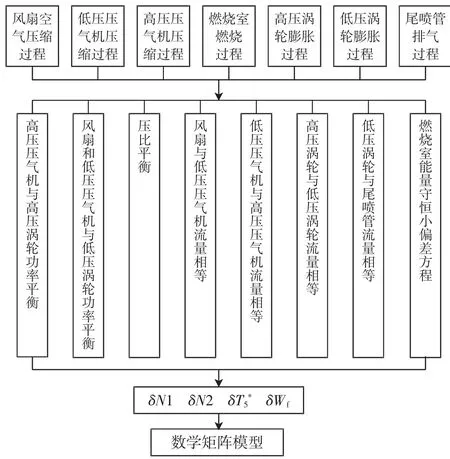
图4 矩阵模型建立过程Fig.4 Building process of matrix model
通过以上流程图的求解,得出关于低压转速(N1)、高压转速(N2)、排气温度EGT(T5*)和燃油流量(Wf)的表达式,即


将上述结果以矩阵表示,求得方程形式为y=Ax
为求解上述数学模型的系数矩阵A,需要各单元体进出口的总温和总压,虽然可以通过理论计算获得,但在部件特性未知的情况下,很多因素需要假设,导致计算结果误差很大。为了使计算结果与发动机实际工作情况相近,这些参数可通过发动机实际运行QAR数据获得。每次飞行时所记录的QAR数据都可以认为是发动机的一次正常飞行试验数据。选用PW4000系列发动机QAR记录中某一巡航状态的无故障数据,并根据参数修正公式对所选参数进行修正,结果如表2所示。

表2 修正后的QAR数据Tab.2 Corrected QAR data
各单元体的实际效率根据发动机非设计点模型计算得出[11-12]。将所选数据和计算获得的效率代入偏差方程系数Ki中,得到该巡航状态的系数矩阵A,如表3所示。

表3 数学模型矩阵Tab.3 Mathematical model matrix
3 模型验证与应用
为验证模型的有效性,采集PW4077D指印图[13]上有关单元体的性能衰退征兆量,如图5所示。采集数据如表4所示。

图5 PW4077D指印图Fig.5 PW4077D fingerprints

表4 单元体性能参数偏差Tab.4 MDL performance parameter change

表5 整机性能参数变化量及误差比较结果Tab.5 Parameter change and comparison results of whole engine
由模型计算的参数变化与采集的性能参数变化可知,模型计算的结果与采集的数据较接近,大部分相对误差小于10%,个别误差不超过15%。误差产生的原因可能为没有考虑压气机的引气损失、各单元体的机械效率以及假设了气体在喷管内完全膨胀,喷管为单一涵道,忽略了内外涵道之分。虽然这些会对模型的计算结果造成一定的误差,但通过此方法建立的模型具有可行性。根据此模型结合单元体发生不同故障或同一故障严重程度不同时性能的衰退量可以计算整机性能参数的变化量。建立了单元体性能与整机性能之间的联系。
4 结语
1)在热力计算基础上结合实际QAR数据建立了数学模型,并通过模型得到了转速、EGT(T5*)、燃油流量等性能参数的偏差值,偏差值误差大部分小于10%,表明计算结果比较准确,从而通过模型确定了单元体性能与整机性能参数之间的变化规律。通过模型得到EGT(T5*)、FF的变化值,可以确定单元体对整机性能影响的大小,决定拆发时间,为发动机以单元体为单位的重点维修提供依据。
2)应用小偏差理论,对非线性方程进行线性化处理,相较于传统部件级建模方法利用非线性方程组对性能参数变化的求解,减少了大量的迭代计算,提高了计算速度,节省了计算时间。

