一种基于局部线性嵌入的SVM增量学习方法
(浙江工业大学 信息工程学院,浙江 杭州310023)
随着当今互联网的飞速发展,与此相关的数据也在不断增长并表现出新的特点[1]。支持向量机(Support vector machine)对数据分类有着明显优势,通过对收集的数据(包括有标签样本数据和无标签样本数据)进行学习和分类,发现数据样本中的内在信息,根据这些信息实现对未知样本的预测。
支持向量机(SVM)分类方法因其对简单样本分类精度高、速度快而受到广泛的关注。而对高维样本进行直接分类则存在分类较为困难的情况,因此利用PCA算法对SVM进行改进的方法也层出不穷。在PCA-SVM的基础之上,提出了一种基于局部线性嵌入的SVM增量学习算法。通过流形降维方法,对高维数据进行特征提取,以简化分类器训练的复杂度,在读入数据之后首先对数据进行降维处理,随后再以降维后得到的低维空间数据作为训练数据送入SVM分类器以实现初次训练,在后续增量学习的过程,对新增数据利用流形方法降维后,先获取新增数据降维之后在低维空间上的对应数据,随后利用低维空间的SV集寻找SV集附近的新增数据,其他距离SV集较远的新增数据,即可视为对本次增量训练过程的新SV影响很小的新增数据,因此仅将本次增量学习需要参与训练的新增数据与SV集进行增量学习过程训练得到新的SV集。
1 算法实现
1.1 算法描述
降低数据维数的方法主要分为线性降维和非线性降维,其共同特点是从已知样本数据中学习到一个映射矩阵,然后通过与映射矩阵的线性运算将样本降维到低维特征空间之中。线性降维计算方法较为简便,降维方法主要包括主成分分析(PCA)[2]、多尺度分析(MDS)[3]和线性判别分析(LDA)[4]。非线性降维主要以等距映射算法(ISOMAP)[5]、局部线性嵌入算法(LLE)[6]为代表。
因PCA降维方法与SVM分类器结合的过程快速准确,被广泛应用于SVM分类过程,而基于PCA的改进算法也层出不穷。非线性降维方法就是一种可行的方法,可分为全局降维和局部降维两种,经典的全局算法为等距映射(ISOMAP),而局部线性嵌入(LLE)、拉普拉斯映射(LM)[7]、局部切空间对准(LTSA)[8]和黑森特征映射(HE)[9]等都是经典的局部算法。
基于PCA-SVM分类过程的特性研究,提出了支持向量机的LLE-ISVM的增量学习方法,并在此基础上提出了一种利用SV集选取附近新增训练样本进行增量训练的方法。该算法首先对每一轮当前增量训练的训练样本进行LLE降维得到低维特征向量,并在增量训练之前利用低维特征空间SV集对新增训练样本进行筛选和约减,保留了最有可能成为支持向量的训练样本集进行增量训练,随后以SV集与筛选后的新增样本进行训练,保证了算法的准确率以及速率。算法大体流程如图1所示。
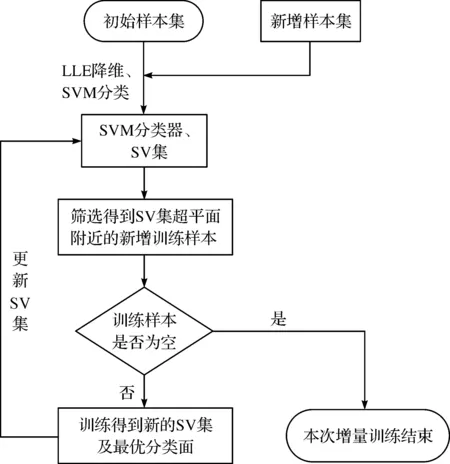
图1 LLE-ISVM算法流程Fig.1 The algorithm of LLE-ISVM
1.2 支持向量机(SVM)原理
支持向量机[10-11]可以理解为是一个二分类器,它对于给定的包含正负样本的训练样本集,寻找出一个分类超平面,如图2所示,使得分开的两个类别具有最大的分类间隔,即使得分类超平面H和两类的支持向量H1,H2所组成的超平面距离最大,这样就得到了一个对于给定数据样本的分类超平面H。对于线性可分问题,可直接利用现有数据进行分类。而对于线性不可分问题,则需将数据集利用核函数映射,得到线性可分数据后再进行分类。
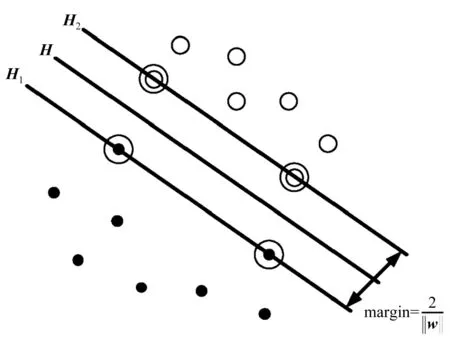
图2 支持向量机分类超平面Fig.2 Thehyperplane of SVM classifier
假设现有数据集T={(xi,yi)},i为初始训练集的数据点个数,xi为数据的特征,yi为对应数据的标签,取值正样本为+1,负样本为-1。对于分类超平面而言,其表达式为
H:g(x)=wTx+b=0
(1)
H1:y=wTx+b=1
(2)
H2:y=wTx+b=-1
(3)
其中:w为分类超平面的法向量;b为分类超平面的偏置[12]。
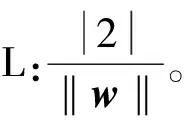
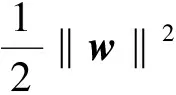
wTxi+b≥+1,yi=+1
wTxi+b≤-1,yi=-1
因此,最大分类间隔的求解便转化为求取以下最优化问题。对以下问题求解得到最优的(w,b),可得到对于该训练样本的分类超平面,即
Subject towTxi+b≥+1yi=+1
wTxi+b≤-1yi=-1
1.3 局部线性嵌入(LLE)
局部线性嵌入和传统的PCA,LDA等关注样本方差的降维方法相比,更关注降维时保持样本局部的线性特征,由于LLE在降维时保持了样本的局部特征,它广泛地被用于图像识别、高维数据可视化等领域。
LLE算法大致可分为如下步骤:每个样本点的k个近邻点选择[13]、构造局部重建权值矩阵、低维嵌入向量计算。假设有训练集T={(xi,yi)},i为初始训练集的数据点个数,xi为数据的特征,yi为对应数据的标签,低维空间为d维,计算步骤为
近邻点选择。算法的第一步是计算出每个样本点的k个近邻点。把相对于所求样本点距离最近的k个样本点规定为所求样本点的k个近邻点。
构造局部权值矩阵W。对每个样本点xi与其k个近邻点的局部重建权值矩阵,求出局部协方差矩阵,即
Zi=(xi-xj)T(xi-xj)
(4)
定义重构误差,即
(5)

低维嵌入向量计算。利用局部权值矩阵将样本降至低维,通过求解使得降维损失函数最小化的过程,通常特征值按从小到大排列,选取第2个到(d+1)个特征值所对应的特征向量作为输出结果。
1.4 算法步骤
假设初始训练样本集为A0,新增样本集为B0,SV集的原数据样本为S01,对初始样本降维之后训练得到的SV集为S11,增量学习后得到的SV集为S12,新增样本B0与S01降维后得到B0在低维空间中的对应数据集为B1,并将B1与S11比对筛选之后获取到低维样本集T1和对应原样本集T0。LLE-ISVM算法的详细描述为
1) 利用LLE对A0降维后进行SVM训练,得到一个分类超平面H,原始数据SV集S01,低维数据SV集为S11。
2) 将S01与新增样本集B0一同进行LLE降维,得到新的低维空间中的原SV集的低维表达S11(此处已经对S11进行更新)和新增样本的低维表达B1。
3) 计算B1到两个SV集对应的两个超平面H1,H2的距离L1,L2,将保留下列不等式的样本记为B1t,式中K为一给定的实数,即
4) 如果B1t为空集,则本次增量学习过程结束,SV集保持不变,最优分类面保持不变,否则,继续下一步骤。
5) 将S11和B1t合为一个训练集进行SVM的分类器训练过程,得到新的分类面和新的SV集。
6) 更新支持向量集S01,得到新的分类超平面。
2 实验数据及结论
2.1 测试数据
实验测试分别在手写数字数据集MNIST和标准数据集Steel,Waveform上进行。主要以MNIST数据库来说明,因为算法主要是针对较大规模数据,一般为非线性,所以采用核函数(RBF)的SVM分类器,以tic和toc对测试过程进行计时。实验所使用的PC机主频为2.4 GHz,内存为4 G,处理器为i5-2430M,所用的软件为Matlab R2012a。实验将样本数据集随机分成初始样本集、增量样本集和测试集。数据集个数、特征个数和增量详情如表1所示。
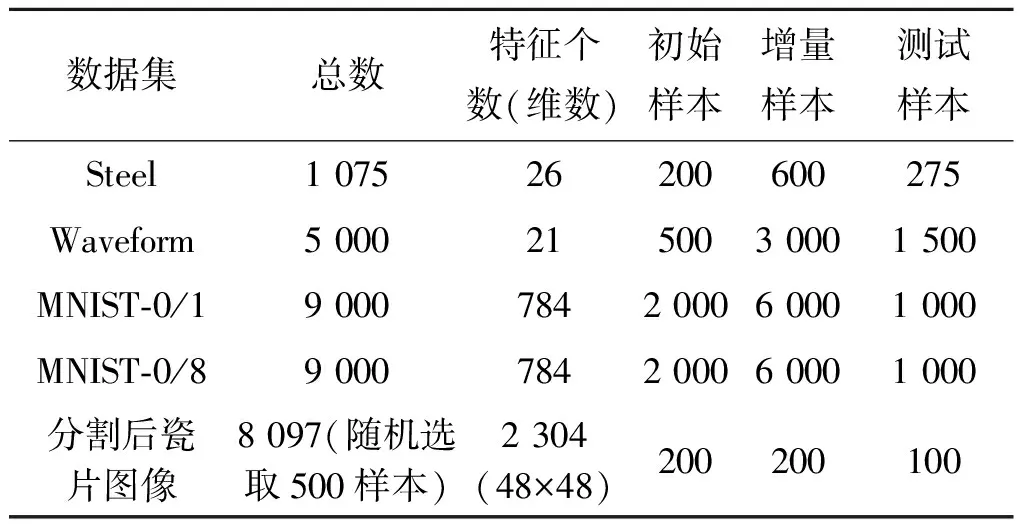
表1 数据集和增量参数Table 1 Dataset and incremental parameters 个
以MNIST手写数据库为例作为测试,选取了其中两组手写数字为“0”和“1”以及“0”和“8”的两类图片为例实现二分类过程,主要以“0”“1”二分类来描述,如图3所示。

图3 手写数据库的“0”和“1”Fig.3 The number “0”and “1” of MNIST dataset
将手写数字“0”标签为“-1”,手写数字“1”标签为“+1”。一共获取到9 000张手写数字“0”“1”的28×28图片,将其中2 000张图像作为初始训练样本,6 000张作为增量样本,每次增量选取其中2 000张图像作为新增样本集,1 000张用于测试。图4为对所获取的其中各200张“0”“1”图像使用LLE降至2维的分布效果图,圆形与菱形则代表两类不同的数据的低维表示。
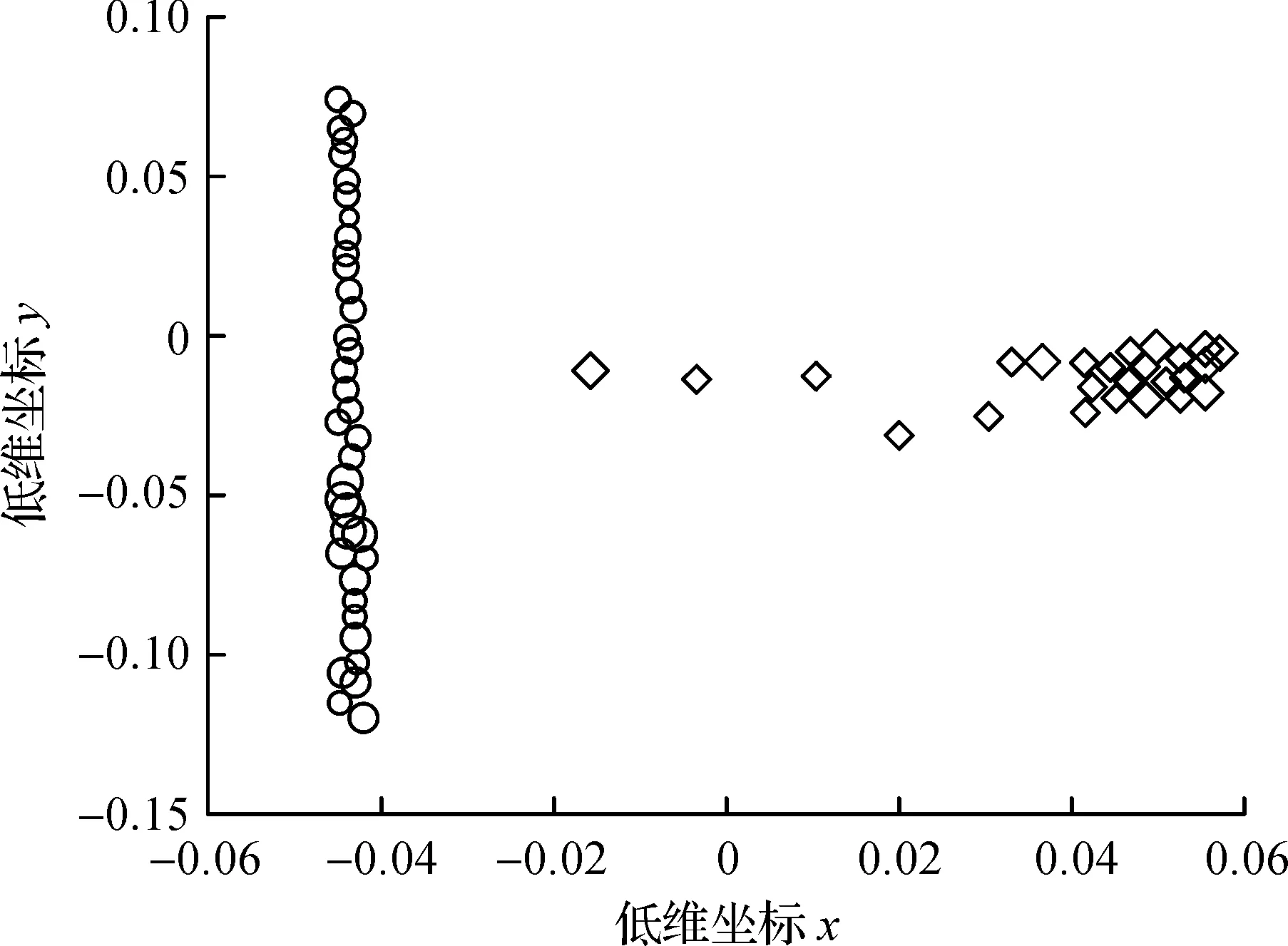
图4 图像“0”“1”的LLE降维的低维空间分布Fig.4 Low dimensional subspace distribution of LLE
在精度方面,主要将LLE-ISVM方法与其他两个方法进行比较:一个是传统的非增量的支持向量机(SVM),另一个是利用PCA降维的增量SVM方法。对于MNIST手写数据库,利用LIBSVM,选取RBF高斯核函数,多项式核函数的参数为3,惩罚函数为0.5,对手写数字“0”“1”进行二分类。对于纯SVM的分类方法,直接对获取到的二值化图像像素值进行归一化,随后将28×28矩阵按行展开成1×784维的行向量,即以一行作为一个样本,将获取到的8 000张训练样本转换成8 000×784维的矩阵形式送入SVM进行分类。对于PCA-ISVM而言,利用主成分分析降低至20维,获取到其前20个特征值所对应的特征向量,随后在20维空间上获取其在该低维空间上的映射,以1×20维的行向量作为一个样本数据,选取2 000×20维的矩阵作为初次分类训练样本,随后将6 000个增量样本分3 次进行增量训练。对于LLE-ISVM而言,在LLE降维过程需要选取k个近邻点,k设置为10,同样降低至20维空间。选取20维作为特征空间得到初始训练集数据在20维空间上的LLE映射,对2 000×20维初始样本集进行初次分类,随后将6 000×20维的增量训练集进行新的LLE映射,与前一次训练所得的SV集进行比对筛选之后,将所得新增训练集与SV集进行新的SVM分类器训练。由表2可知:增量学习过程能够提升分类算法的精度。
表2 增量学习后的精度对比
Table 2 The comparison of accuracy after incremental learning
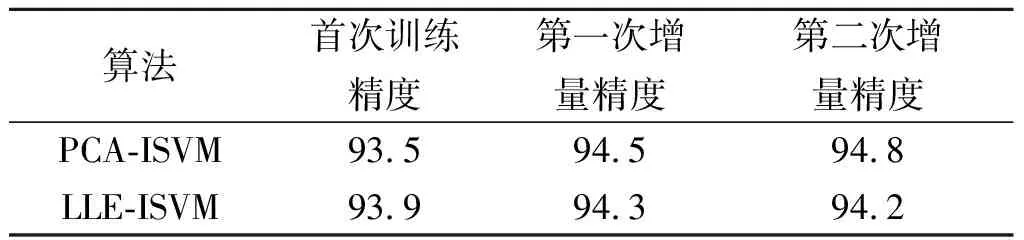
%
为便于对同一组数据分类进行对比,对MNIST的“0”“1”分类以及“0”“8”分类计时,同时也包括对图像的读取、归一化、展开成行向量的过程。得到的最终精度和时间如表3,4所示。
从表3,4可知:由于所选取的测试数据分布规律较为简单,因此LLE-ISVM方法和SVM训练方法在精度上差异不大,但LLE-ISVM方法能有效地提高训练的速率。对比PCA-ISVM过程可以发现:MNIST数据库的二分类过程中两种算法训练精度较为接近,速度上LLE-ISVM方法较PCA-ISVM有小幅提升。实验数据表明:LLE-ISVM作为一种类比PCA-ISVM的方法,能较好地适应MNIST数据的分类,相比SVM有较大提升,同时在参数(分类模型、k近邻个数、新增样本距离SV集的距离等)选取恰当时,在保证训练精度的前提下,LLE-ISVM在训练速度上相比PCA-ISVM有小幅提升。
表3 不同算法分类精度
Table 3 The comparison of different algorithm classification accuracy
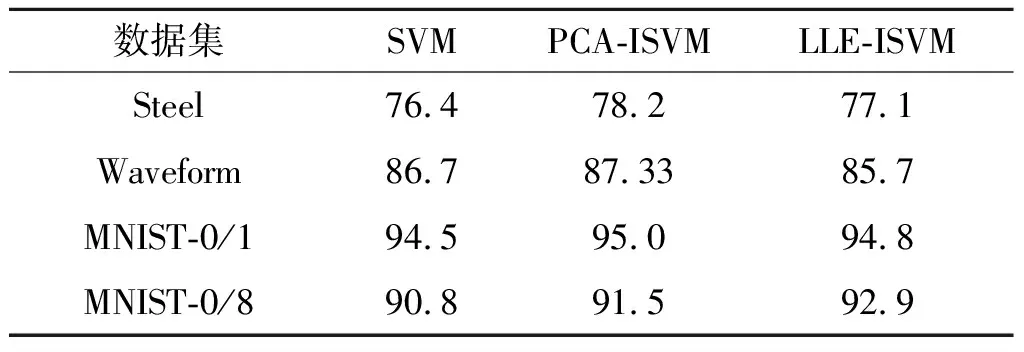
%
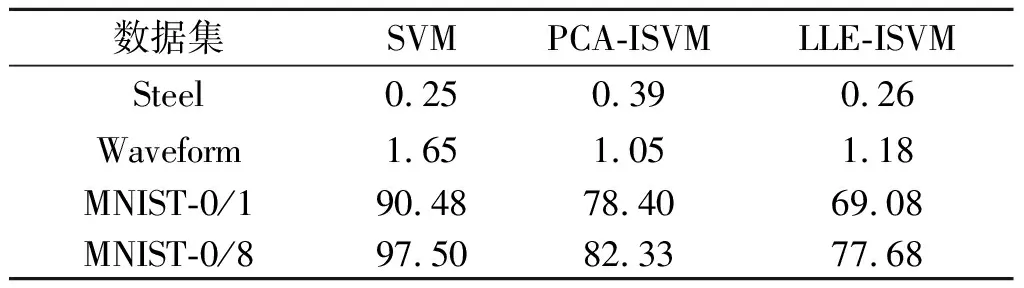
表4 不同算法训练总时间Table 4 The time of different algorithms training process s
2.2 测试结果
将LLE-ISVM算法应用于瓷片表面缺陷检测过程,由于所获得的原始图像维数较高,因此首先对图像进行分割后得到48×48维的分割图像,选取其中500张图像进行测试。部分样例图片见图5。

图5 缺角瓷片和完好瓷片Fig.5 The defective pictures and normal pictures
最终以其中200张图像进行首次训练,200张图像分4次进行增量学习过程,其中100张作为测试图像。最终得到PCA-ISVM方法正确率为71%,LLE-ISVM方法正确率为75%,虽然LLE方法相对于PCA降维算法复杂度较高,但由于该方法对新增样本进行筛选而非全部样本进行计算,因此时间消耗差异不大。但由于LLE分类方法应用于瓷片缺陷检测过程中时准确率较低,目前该算法并不适应当前环境的瓷片缺陷检测过程,后续需对算法进行修正并加以提升后才可运用于实际过程。
2.3 实验结果分析
1) 通过对比MNIST数据库的“0”“1”降维效果,PCA与LLE均能对MNIST数据库的“0”“1”图像进行较好的分离,但LLE的分类效果要优于PCA降维。
2) 对SVM引入增量过程,可以有效地降低训练时间,同时对分类精度有一定的提升。
3) 对“0”“1”分类和“0”“8”分类进行对比,由于LLE降维过程复杂度高于PCA,若以新增分类样本直接进行LLE-ISVM训练,训练时间会明显高于PCA-ISVM过程。与PCA降维算法相比,由于LLE降维过程比PCA降维复杂度高,因此直接使用LLE降维会使训练时间变长,而LLE-ISVM选用的对新增样本进行筛选的策略能有效地提升运算速度,因此总体上来看LLE-ISVM对运算速率是有一定提升的。同时LLE算法对高维图像进行降维时能更好地保留图像的原始特征,因此也能有足够高的判别准确率。综上所述,在维数较低时PCA-ISVM与LLE-ISVM大体上均有较好的分类准确率与速率。
4) 当利用LLE-ISVM算法对较高维度的瓷片图像进行测试时,该算法的准确率比PCA-ISVM要高出4%。在训练时间基本一致的前提下,LLE-ISVM能较好地处理高维数据的分类。由于LLE-ISVM并没有对图像进行特征提取,因此所得到的准确率整体偏低,仍存在训练时间较长的问题,在对实际瓷片缺陷检测过程中实用性较低。因此利用LLE-ISVM对瓷片图像进行分类的应用仍需要改进。
3 结 论
通过对比实验数据可以发现:LLE降维方法对手写图像的简单降维分类效果要优于PCA降维方法,而LLE在计算复杂度上相对于PCA较高,如果对全部样本进行降维后分类,会存在耗时较长的问题,因此引入对SVM分类器的增量学习过程。可以发现LLE-ISVM增量算法对新增样本的筛选能有效地降低算法的运算时间,在完成分类过程的同时有较高的准确度和速度,能实现完整增量学习过程。由于对新增样本点筛选对算法速度的提升较为有限,其本质是由于LLE的计算复杂度比PCA高,因此未来计划对LLE降维算法进行改进,以提升LLE算法的分类精度和计算速度。由于LLE降维过程能更好地获取和保留数据的原有流形结构,在保证速度的同时,LLE-ISVM相较于PCA-ISVM方法能更为准确地实现磁片表面的缺陷检测分类过程。但在实际的瓷片缺陷分类过程中,由于所获取数据的分类精度较低,暂时不能用于瓷片缺陷检测,算法还待改进,笔者所使用的SVM方法是传统的监督学习过程,该算法的泛化能力较弱,同时实际应用之中,更多的是少部分有标签、大部分无标签的数据,监督学习过程是较为低效的,后续需要采用LLE降维方法对样本进行筛选,对样本进行半监督学习过程,以更好地提升该算法,使之能更好地应用于瓷片表面缺陷检测过程。

