基于分层控制结构的迭代学习城市交通信号控制
(浙江工业大学 计算机科学与技术学院,浙江 杭州 310023)
由于城市交通网络规模庞大、结构复杂,国内外交通研究人员对大规模城市交通网络的分层控制进行了研究。其中澳大利亚的SCATS[1]是典型的具有3 层结构的交通自适应协调控制系统。Ramezani等[2]提出了一种基于宏观交通模型的分层交通控制结构,通过预测控制方法和边界控制器调节边界控制信号以最大化相邻区域的车辆输出。沈国江等[3-4]基于分层结构计算子区公共信号周期、上下行相位差和各路口的绿信比。Zhou等[5]针对大规模的城市交通网络提出了2 层的模型预测控制框架,实现子区间的交通需求平衡。此外,还有一些城市交通分层和管理控制方法在文献[6-8]中提出。
上述提出的大多数交通分层结构的控制方法都需要车辆空间分布矩阵OD(Origin-Destination)以及精确的交通模型信息。然而,城市路网交通系统是一个不确定的复杂系统,其车辆分布以及模型参数难以确定。宏观基本图(MFD)[9-12]和迭代学习控制(ILC)[13-17]仅利用实测交通数据和少量的模型信息即可解决路网信号控制问题。因而笔者提出一种基于分层结构的迭代学习交通信号控制策略。上层基于交通数据,获得路网各子区对应的MFD,进而设计各子区理想的道路占有率,下层基于简化的道路交通流模型,采用开闭环ILC控制方法获得子区内各路口的信号配时,使子区内的道路占有率达到上层的要求,从而使路网内车辆密度达到均衡分布的效果,并提高了路网的整体通行能力。
1 分层结构的交通模型及问题描述
1.1 上层MFD模型
选取1 个包含3 个子区的城市路网作为分层控制的对象。定义各个子区为R1,R2,R3,如图1所示。
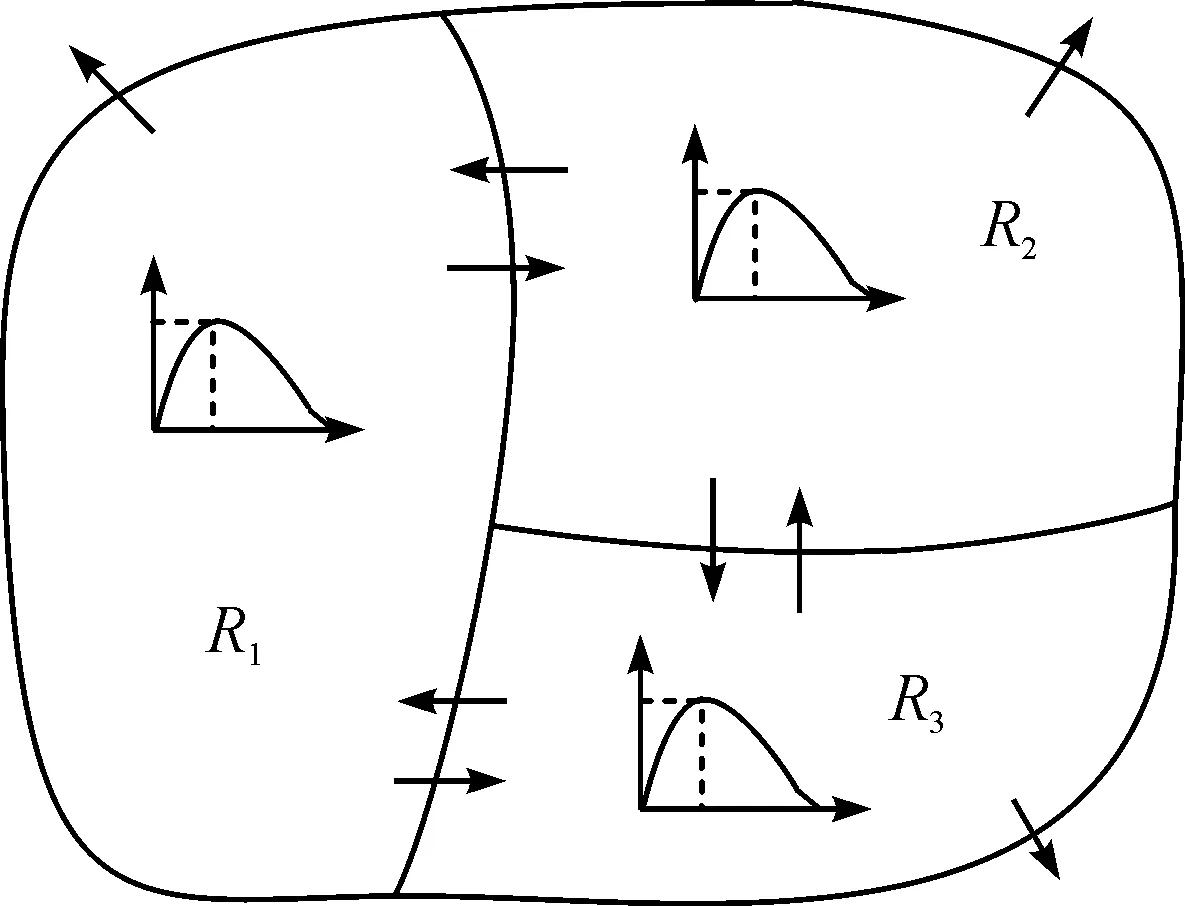
图1 路网结构图Fig.1 Structure of the network
根据Geroliminis等[12]的研究,路网内各子区对应的加权流量和该子区内的累积车辆数呈一种非线性关系,可用MFD曲线描述。对于图1路网中的任意子区Ri,i∈{1,2,3},其加权流量为
(1)

(2)


图2 路网的宏观基本图Fig.2 Macroscopic fundamental diagram
在0~n1阶段,路网的车辆较少,路网整体相对自由,但是驶离路网的车辆数也较少。此时路网处于欠饱和的状态,路网对绿灯信号的利用率也较低,存在大量绿灯空放等现象。在这个阶段,通过调整交通信号的参数(绿信比、周期、相位差),路网的绿灯利用率可以得到一定的增加。
在n2之后,路网达到过饱和状态时,路网内部开始回溢并且严重拥堵,驶离路网的车辆急剧减小,最终形成锁死状态。路网将进入一个车辆累积数巨大但实际流量为0的状况。
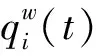
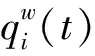
(3)

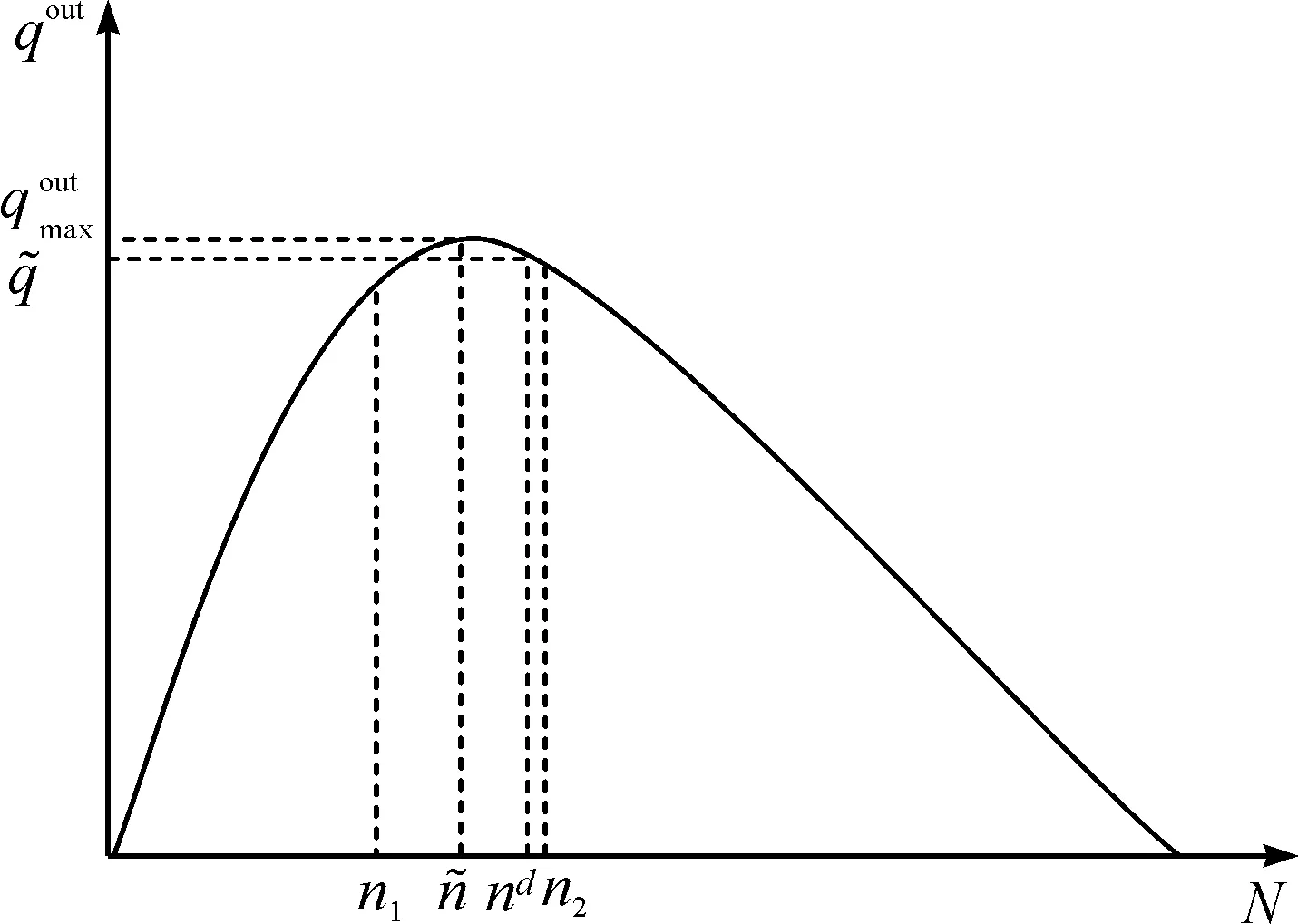
图3 理想累积车辆数Fig.3 Desired numbers of vehicles
由此得到的理想道路占有率od作为下层迭代控制的理想值,使区域内的占有率相对均衡,各子区处于最佳运行状态,获得较大的区域流出量,进而提高路网的通行量。
1.2 下层改进的交通流模型
由于交通路网的结构过于复杂,难以得到精确模型,下层采用一类简化的交通流模型对城市交通路网进行建模,如图4所示。
图4 交通流模型Fig.4 Model of traffic flow
图4中展示了城市路网中交叉口和道路的基本情况。定义路网中的交叉口集合J,图4中两相邻路口{j1,j2}∈J,连接2 个交叉口的路段为zo根据道路中车辆守恒这一规律,路段z中的动态交通特性可以描述为

(4)

路段z的输出流率满足
(5)
式中:gj2,p(k)为交叉口j2的相位p的绿灯时间;Sz为路段z的饱和流率;T为周期时间;Fj2为交叉口j2可选相位集合。
路段z的输入流率满足
(6)
式中:Iw为j1相邻上游路段w的集合;τw,z为路段w经过交叉口j1进入z路段的转向比。对于同一路段上的转向比,满足
(7)
根据式(5,6),输入流率又可转换为
(8)
根据式(4,5,8),受控路段z交通流的动态平衡方程为

(9)
对于每一个交叉口j,其相位绿灯时间为gj,p,则损失时间Lj和周期时间T必须满足
(10)
路网的状态空间方程可表示为
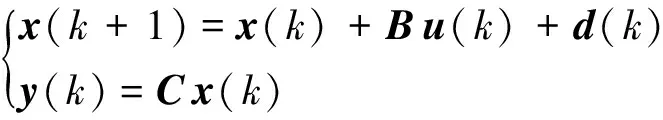
(11)
式中:x(k)=[x1(k),…,xN(k)]T为状态向量,表示路网中各路段包含的车辆数;u(k)=[g1(k),…,gN(k)]T为控制向量,表示路网中所有相位的绿灯时间;d(k)为状态扰动向量,表示各路段的扰动;y(k)=[o1(k),…,oN(k)]T为系统输出,反映路网中各路段的占有率;B为输入矩阵,反映了路网的相位、周期、饱和流量等特征;C为输出矩阵,表示道路容量和车辆长度的特征。
由于在交通系统中,考虑到车辆的启动、紧急制动、行人的过街时间以及驾驶员的心理,绿灯时间既不能太大也不能太小,必须设置在一个合理的范围内,因此在模型中必须对控制变量进行限制为
(12)
式中:umin为最小绿灯时间;umax为最大绿灯时间。得到受限情况下的状态空间方程为
(13)
2 控制目标
3 控制方法
3.1 上层子区MFD拟合
如1.1节所示,描述路网累积车辆数与车流率之间的MFD特性函数可用拟合的方式得到。由于输入流量不影响路网内MFD的特性,但是控制信号的改变会影响MFD特性,因此采用多组信号配时对路网进行仿真,获取路网的车辆累积数和流量数据,将多种不同信号控制情况下的流量和车辆累积点画在同1 张图上,以获得更合理的MFD拟合曲线。
采用最小二乘法对各个子区Ri进行MFD拟合,拟合结果用3 阶多项式形式表示为
(14)
式中:a1,a2,a3为拟合系数;ni为子区的累积车辆数,由实际路网测量数据或者仿真数据验证得到。根据偏差平方和最小的条件来确定经验公式中的常数项为
(15)
式中:i∈{1,2,3};ni为子区Ri的累积车辆数;yi为子区Ri的实际输出流量值;G(ni)为子区Ri输出流量的近似拟合曲线。式(15)的目标是最小化数据偏差平方和,从而得到MFD多项式的近似表达式。
3.2 下层开闭环ILC方法
对于1.2节得到的式(13)描述交通路网的状态空间方程,采用迭代学习控制的方法。但是考虑到城市干道交通系统的日重复特性存在波动,单一的前馈控制很难达到令人满意的效果,因而引入反馈控制来解决迭代过程中扰动的影响。开闭环迭代学习控制同时包括前馈和反馈控制,能够有效利用在离线交通数据,获得理想的控制效果。开闭环迭代学习控制的系统结构图如图5所示。
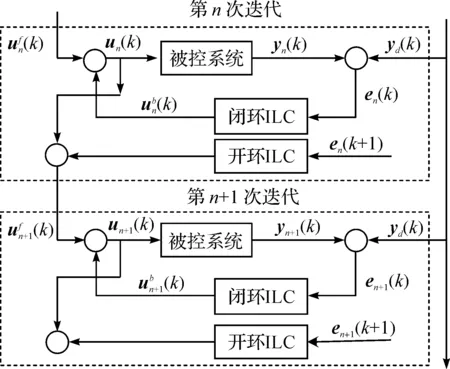
图5 开闭环迭代学习控制Fig.5 Open and closeloop ILC
开闭环迭代学习控制的结构可以表示为
(16)

对于交通系统,各个路口的绿灯时间作为开闭环迭代学习的控制输入un(k),各路段的道路车辆占有率作为输出yn(k)。通过设定合适的迭代学习控制律,调整交通路网内的绿灯配时信号,追踪上层MFD设定的理想道路占有率的目标。
4 交通仿真应用
为了有效评价控制算法的效果,在本节中将通过Matlab和Vissim仿真软件对路网进行仿真控制。测试路网采用图6所示的结构,由34 个交叉口和154 条道路组成。为了得到具有多子区的路网结构,现按文献[18]将路网中划分为包括R1,R2,R3的子区,结构如图6所示。
参数设置如下:周期时间T为60 s,采样周期为60 s,仿真时长为5 400 s,车辆的平均长度为6.7 m,由外围节点s1~s21提供输入流量,迭代学习控制的开环学习率选择为ko=-1,闭环学习率选择为kc=-1。
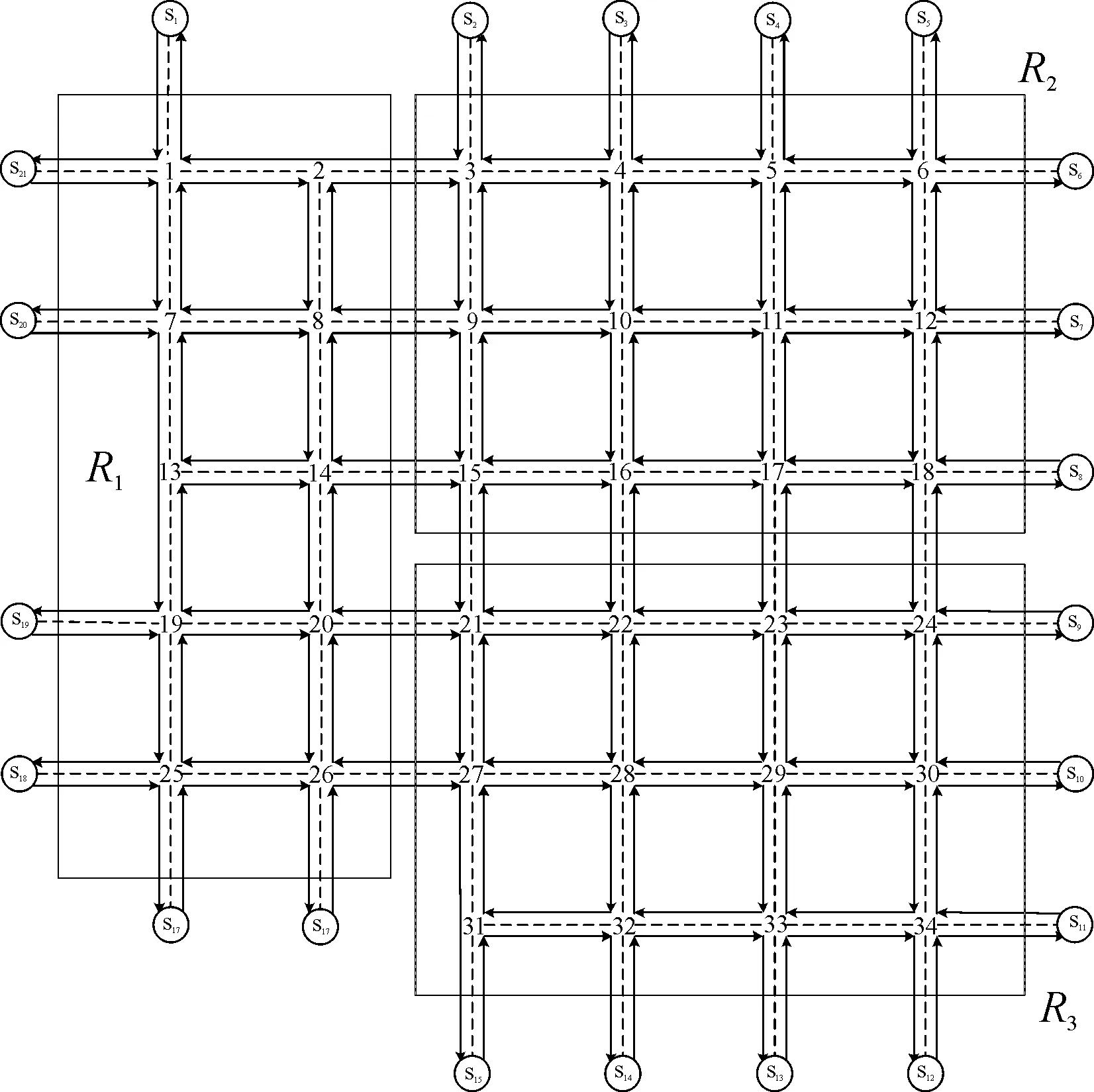
图6 测试路网Fig.6 Urban traffic network
3个子区R1,R2,R3的MFD特性曲线的拟合函数分别为
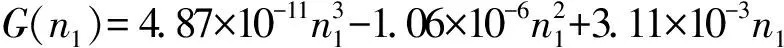
拟合曲线结果如图7所示。
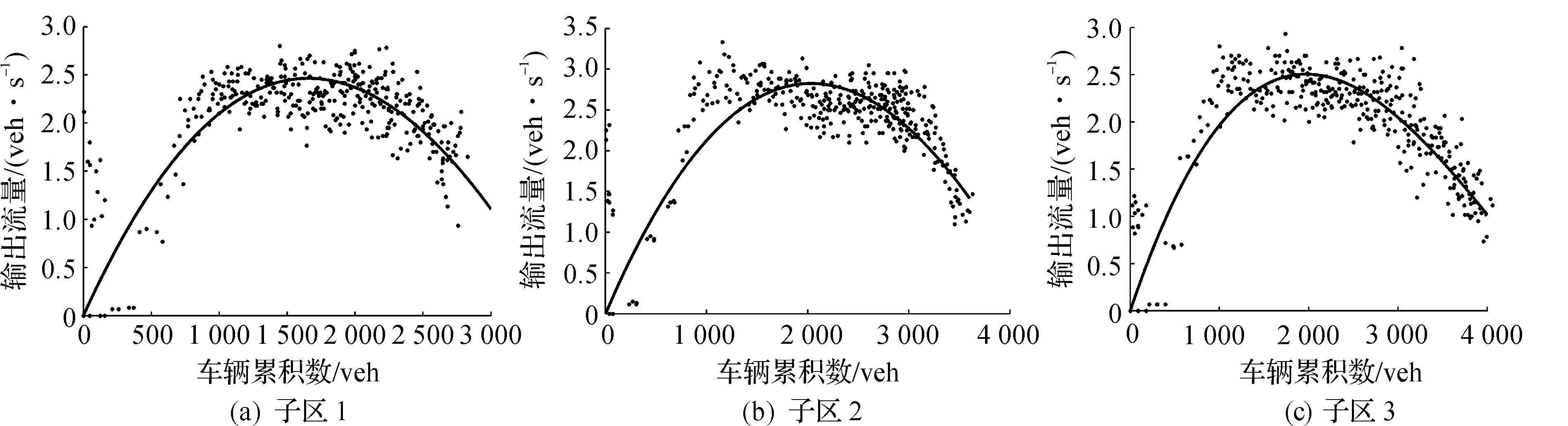
图7 各个子区的MFD拟合曲线Fig.7 MFD fitting curve of each network
根据拟合结果得到各子区理想的道路占有率od作为下层迭代学习的参考,得到各个子区内的信号配时方案,并与经典的Webster定时方案作对比。Webster定时方案是定时信号控制中应用最广泛的控制算法之一[19-20]。现考虑两种场景分别采用笔者提出的分层控制算法和Webster定时方案对路网进行仿真测试。如表1所示,场景1中的输入流量保持不变,场景2中的输入流量随着仿真时间的增加而递增。
图8展示各子区在不同输入流量场景两种控制方法下的子区输出流量情况。实线表示笔者提出的分层迭代学习控制策略(ILC-based),虚线表示Webster定时方案(Fixed-Time)。其中图8(a~c)为场景1中各子区输出流量变化,图8(d~f)为场景2中各子区输出流量变化。可以看出:随着仿真时间的推移,Webster定时方案的输出流量下降得更剧烈,分层迭代学习的控制下使各子区的输出流量保持较高水平。

表1 路网周期输入流量Table 1 Input flow of network

图8 两种场景下的各子区输出流量Fig.8 Outflows of subnetworks in scenario 1&2
图9(a,b)分别展示了场景1中Webster定时方案下的道路密度情况和分层迭代学习控制策略下的道路密度情况,其中横坐标表示控制周期,纵坐标表示道路。颜色越深表示密度大。可以看出:分层迭代学习控制策略相较于Webster方案,道路整体车辆密度更加均衡,拥堵程度减小。图9(c,d)分别展示两种控制算法在场景2下道路密度情况,分层迭代学习控制依然比Webster固定配时的效果好,路网的密度更加均衡。
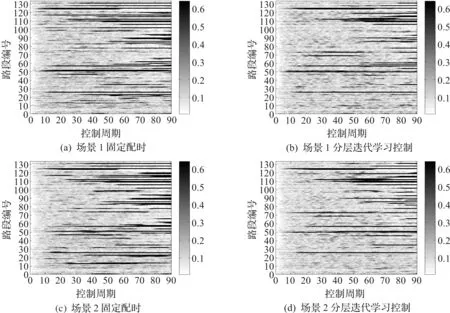
图9 两种场景下的道路密度Fig.9 Density of network in scenario 1&2
另外,通过Vissim的评价文件,得到路网的行程时间和延误时间这两种指标,如表2所示。

表2 不同输入流量下的路网性能比较Table 2 Comparison of road network performance
在场景1中,Webster定时方案下,路网中的平均延误时间为583.9 s,在使用笔者提出的分层迭代学习控制方法时,平均延误降低到459.2 s,整体的延误时间下降了21.36%,同时路网的行程时间也从836.0 s下降到了702.8 s,性能提升了15.93%。同样的,在场景2的变流量输入的情况下,路网的行程时间下降了6.42%,平均延时时间下降了12.43%。结果显示两种情况都大大提高了路网的通行效率。
5 结 论
针对城市路网的特点,提出了一种基于分层结构的迭代学习控制策略。上层对多子区路网进行MFD的多项式拟合,并利用路网均衡的思想对车辆累积数进行分配,进而得到下层的理想道路占有率。下层通过迭代学习控制,获得各个交叉口信号配时方案,使子区内部占有率达到上层设计的理想占有率。通过Vissim对城市路网进行仿真,在两种不同输入流量的情况下对路网分别采用Webster固定配时和分层迭代学习信号控制策略,对比显示分层迭代学习信号控制策略使路网车辆更加均衡,提高了路网整体通行能力。

