经验积累与方法内化——一般三角形面积公式探索

□汪 杰

【课前思考】

“一般三角形的面积”一课，在面积公式推导序列中处于承前启后的地位。在本课教学之前学生学习了直角三角形的面积公式，在本课教学之后将继续探究其他平面图形的面积公式，需要学生具备比较熟练的图形转化技能，积累相应的公式推导经验。而这些经验与方法的储备，都需要借助本课中“图形转化”与“公式推导”两项活动来进行。围绕这两项活动，笔者重点思考了以下两方面问题。

1.图形转化方法有几种？按照学生现有的认知基础，一般会出现三种方法。第一种是“倍拼法”，即将三角形沿高线分割成两个直角三角形，通过翻倍旋转拼成一个大长方形。第二种是“剪拼法”，即将三角形沿高线中点并垂直于高剪开后旋转拼成一个长方形。第三种是“分割法”，即把三角形沿高线分割成两个直角三角形，求出面积和。

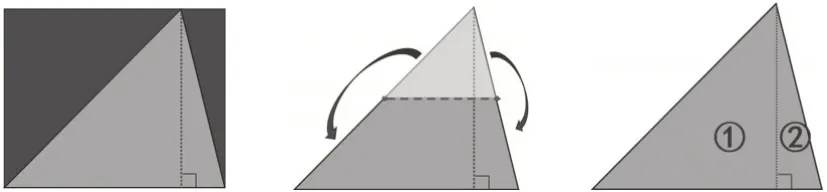
面积=底×高÷2面积=底×（高÷2） 面积=（底①＋底②）×高÷2

倍拼法与剪拼法依托的是直觉思维，通过直观操作来实现转化，不管是两次倍拼，还是利用中位线实现双向剪拼，都有助于发展学生的想象能力与创造思维。而分割法蕴含着化繁为简的思想，适用范围最广，但在公式推导时需运用乘法分配律进行公式合并，对学生的学习能力要求较高。

2.公式推导路径是怎样的？在图形转化后，首先进行新旧图形关系判断，其中“倍拼法”属于非等积转化，其形成的长方形面积是三角形的2 倍。其次进行公式的演绎推理，把新图形公式中的元素替换成与之对应的三角形中的元素，从而得到新的公式。例如，“三角形的面积=长方形的面积÷2=长×宽÷2=底×高÷2”，整个过程就是一种等量代换。最后，由一个三角形的研究结论推广到所有的三角形，渗透从特殊到一般的论证思路，感受数学结论的科学性与严密性。

【课堂实践】

环节一：回顾旧知，激活经验

（板贴一个锐角三角形图）

师：这节课我们继续来研究三角形的面积，这是一个锐角三角形，你认为它的面积与哪些知识有关呢？

生：与它的底和高有关系。因为我们已学的直角三角形与长方形的面积都跟底和高有关。（呈现上述图形面积公式）

师：有道理，那锐角三角形的面积公式该怎样研究呢？

生：想办法把锐角三角形转化成长方形或者直角三角形。（板书：转化）

（设计意图：引导学生回顾相关已有知识和方法，激活经验，明确目标。）

环节二：探究一个锐角三角形的面积计算方法

1.呈现任务：锐角三角形的面积计算。

（1）想一想：把锐角三角形转化成什么图形呢？把想法画出来。

（2）说一说：锐角三角形面积与新图形面积之间的关系。

（3）写一写:锐角三角形的面积如何计算呢？

2.学生独立探究，教师巡视指导。

3.个体汇报，全班交流。

反馈一：倍拼法。

师：（指着高）为什么要沿着这条线分呢？它是三角形的哪部分？

生：它是高，这样分就有两个直角三角形了，翻倍就能形成长方形。

师：哦，你们懂他的方法吗？试着说说是如何倍拼的。

（全班同学自由说后，继续汇报学习单）

生：我发现：锐角三角形的面积=大长方形的面积。算式是5×4÷2=10。

生：不对，翻倍才得到长方形，三角形的面积应该是它的一半。（学生认同后，增添“的一半”三字）

师：那5×4÷2每个数字表示的是什么意思呢？

组织学生说理达成共识：“5×4”表示长方形的面积，“÷2”表示一半，并在下面标注为“底×高÷2”。

反馈二：剪拼法。

（1）观察剪拼的过程，辨析：为什么要沿着高的一半剪开？

得出：只有将一半处剪下来的三角形与缺的部分才能完全重合。

（2）讨论：算式“5×2”中每个数到底表示什么？

重点理解“2”其实是高的一半得来的，把算式修改为“5×（4÷2）”，并在下面标注为“底×（高÷2）”。

4.比较分析。

（同一张PPT 出示2 种方法的图、算式及文字标注）

师：同学们，想一想这些方法之间有什么共同的地方？

生：都把三角形转化为我们学过的图形。这样就可以用已有的公式计算了。

生：每种转化方法都画了高。

师：高有什么用呢？

生：高是垂直于底的线段，它有直角，这样才能变成长方形或直角三角形。

生：每种方法都有÷2，还有底×高。

（设计意图：本环节首先让学生亲历转化过程，获得直接的操作经验；其次再组织观察、辨析、想象等活动，积累丰富的替代性经验；再依托算式进行说理，建立图形间的联结，为公式的推导埋下伏笔；最后通过比较分析，体会高作为三角形基本要素的关键作用。）

环节三：推导所有锐角三角形与钝角三角形的面积公式

（课件呈现不同的锐角三角形与钝角三角形图）

师：那是不是任意一个锐角三角形面积都是“底×高÷2”呢？如果是钝角三角形呢？是不是所有的三角形面积都是“底×高÷2”？让我们打开学习单，同桌合作来展开证明。

1.同桌合作完成学习单。

2.集体反馈。

（1）展示倍拼法作品，教师追问：所有三角形都可以倍拼成大长方形吗？

生：是的，每个三角形都有底和高，只要沿着高分开，左右翻倍都可以。

课件动态旋转上述三个图形后，教师追问：这样斜放置的三角形也行？

学生演示说明：以这条边做底，它可以分成两个直角三角形，倍拼后的长方形是这样的！（课件呈现对应的长方形图）

（2）师生合作借助递等式完成推理后，组织全体学生修正自己的推理过程。

（3）解释：“底×高”指的是什么？为什么一定要“÷2”呢？

（4）展示剪拼法作品，学生互相解释，完成推理过程，讲清“高÷2”是什么。

（5）总结公式。

3.回顾过程，整理结论。

师：下面我们来回顾三角形面积公式的推导过程。

根据学生回答板书：图形转化—关系判断—公式推导—结论推广。

（设计意图：借助多个不同类型、不同长度、不同位置的三角形进行图形转化与公式推导，锤炼学生的推理能力，形成完整的公式探究程序。）

环节四：应用公式解决问题

1.锐角三角形的底是7cm，高是4cm，求面积。

2.直角三角形三条边分别是3 cm，4 cm，5 cm，求面积。

3.等腰三角形三条边分别是5 cm，5 cm，6 cm，求面积。

讨论（1）：“7×4”表示什么？能在你所说的图形上指一指吗？为什么“÷2”？

讨论（2）：有同学列式：“7×（4÷2）”，你看得懂吗？能来讲给大家听吗？

讨论（3）：第2题为什么不选择数据5 cm？

讨论（4）：第3 题为什么不能用所学公式求出面积？

（设计意图：做习题的目的不仅是为了公式的应用，更是为了挖掘知识背后更深层次的内容，引导学生建立图示、算式、公式之间的意义联结，体会对应的底与高是求面积的关键。）

【课后思考】

一、合理使用载体，让经验生长有迹可循

数学活动经验需要在“做”中积淀，它是一个逐步积累的过程。在初次探究锐角三角形面积时，教师提供方格背景，让隐藏的高线与中位线显性化，从而降低操作与验证难度，使学生获得丰厚的图形转化经验。在得到多种算法后，借助算式辨析含义，让学生寻找数与形的对应，沟通形与形的联结，充分感悟公式背后的几何意义。最后完成公式推导，让学生经历观察、模仿、修正等过程，在不断的等量代换中，形成严密而又简洁的书写格式，为后续的公式推导提供实践经验。

二、精心设计问题，让数学理解入木三分

数学深度理解是对数学知识、数学对象的本质的理解。例如在交流图形转化方法后，教师设问：“为什么都用到了高？”引导学生把视角聚焦于高的本质是垂直线段，从而感悟到转化前要思考新旧图形间的特征；又如在公式推广的过程中，动态旋转图形后设问：“这样斜放置的三角形也行？”打破底在水平位置的定式，发现实现转化的本质是能割成两个直角三角形。