DR-RDC:基于校准否定约束集的数据修复方法
卢 菁,党延领,刘 丛
(上海理工大学 光电信息与计算机工程学院,上海 200093)
1 引 言
随着数据的爆炸性增长,劣质数据随之而来,极大降低了数据的可用性.国际著名科技咨询机构Gartner的调查显示,全球财富1000强企业中超过25%的企业信息数据存在不一致性问题[1].如何提升数据质量成为当前研究的热点,各种数据清洗模型应运而生.其中包括:
1)最优化修复模型.文献[2]查找一个既满足预定义函数依赖,又满足修复代价最小的方案来修复数据.文献[3]使用统计方法抽取一个样本,域专家对此样本进行检查和编辑,并重复调用自动修复或增量修复方法,直到所得修复结果的精确度符合预定界限.文献[2,3]基于一种或多种目标约束条件,不增加或删除任何记录,通过修改某些字段,使数据集符合预设的一致性要求,产生单一的最优化修复方案,然而不一致数据的可能修复方案往往不唯一,只根据修复代价最小来判断会忽略具有相似、甚至是相同修复代价的其它修复方案.
2)抽样修复模型.文献[4,5]基于等价类的思想,不局限于单一的最优修复方案,使用抽样方法从所有可能的修复空间中随机产生一种修复,解决修复单一化问题,但因样本集的随机性导致了修复方案的不确定性.
3)按序修复模型.文献[6]考虑修复代价和时序关系,使用关联规则为定位错误数据提供参考,提高了修复错误数据的精度.文献[7]从修复代价和属性值相关性两个方面量化各候选修复方案的可信程度,并最终找出最佳的修复方案.文献[6,7]有效的解决了修复方案随机性问题,但都是通过放宽某些约束条件来计算属性值的优先级,不可避免地影响了修复结果的准确度.
4)融合函数依赖、条件函数依赖和否定约束的整体修复模型.文献[8,9]将不同类型的约束规则融入冲突数据集中,综合考虑各类约束规则之间的交互性,采用整体修复的思想对数据进行清洗.该方法既解决了文献[2-7]所考虑的约束规则不能包含大于或小于的语义约束问题,又解决了单纯将各类约束规则以线性方式或交错方式作用于数据集的问题,但其忽视了约束规则之间可能存在的冲突及对数据集的符合程度.
目前,数据不一致性修复研究中,仅有少量文献考虑约束规则的检测.文献[10]基于统计的置信度方法,假定数据中仅存在很小一部分错误,则违反函数依赖的数据越少,其成立的可能性越大.该方法没有考虑数据语义,检测结果通常含有大量无效的函数依赖.文献[11]基于数据语义置信度的方法,使用条件概率求出给定函数依赖的置信度.该方法只考虑错误元组对函数依赖置信度的影响,根据置信度的大小来判断函数依赖对数据集的符合程度,并未涉及函数依赖之间的冲突检测.文献[12]通过扩展阿姆斯壮定理,开发规则推理系统来分析条件函数依赖之间存在的冲突及其对数据集的符合程度.该方法认为,如果元组与条件函数依赖中的常量相匹配,则支持该条件函数依赖,但否定约束中可能不含常量,所以该方法不适合否定约束之间的冲突检测.
综上,我们提出了基于校准否定约束集的数据修复方法,DR-RDC(Data Repair Approach based on Revised Denial Constraint Sets),主要贡献包括:
1)我们利用否定约束发现算法挖掘出所有约束规则,提出符合度记分函数的概念,计算出每个否定约束对数据集的符合程度,剔除符合度小于阈值λ的否定约束.
2)我们提出关联矩阵,用来检测否定约束之间存在的冲突及类型,并进行冲突消除,得到校准否定约束集.
3)我们将校准否定约束集作用于原始数据集,得出证据规则集及对应的冲突元组集.
4)我们提出DR-RDC方法,以修改最少元组为目标,根据每个证据规则的符合度分数,从高到低地选取证据规则修复检测出的冲突元组集,始终选取条件概率最大的属性值作为冲突属性的修复值,直到冲突元组集不违反任一否定约束.
5)实验表明DR-RDC方法在精确度上优于数据语义置信度方法;对比分析校准否定约束集与原始否定约束集的数据修复效果,发现DR-RDC方法在数据错误检测率和修复率方面具有显著的提升.
2 DR-RDC处理流程
DR-RDC处理流程如图1,输入是原始关系数据集,输出是干净数据集,具体操作步骤如下:
1)利用文献[13]的方法挖掘出所有否定约束.
2)使用符合度记分函数计算出否定约束对数据集的符合程度,剔除小于符合度阈值λ的否定约束,得到高符合度否定约束集.
3)将高符合度否定约束集转化为描述其所包含谓词表达式的关联矩阵.
4)根据关联矩阵检测否定约束之间存在的冲突及类型,进行冲突消除,得到校准否定约束集.
5)使用校准否定约束集对待测数据集进行检测,得出证据规则集及其对应的冲突元组集.

图1 DR-RDC处理流程Fig.1 Processing flow of DR-RDC
6)根据证据规则集中否定约束的符合度分数,从高到低修复检测出的冲突元组集,选取条件概率最大的属性值作为冲突属性的修复值,直到每个否定约束都没有对应的冲突元组集,进而得到干净数据集.
3 否定约束集校准
3.1 否定约束定义
利用约束规则进行数据修复是常用方法,文献[14]对函数依赖和属性蕴含的关系进行了统一建模,旨在分析两者的共性和差异性,并未涉及具体的应用.本文扩展了约束规则的范围,使用一阶逻辑表达式,将约束规则与属性蕴含的关系统一为否定约束,并在此基础上对数据进行检测和修复.否定约束的定义如下.
定义1.否定约束是一种能够表达数据之间各种约束规则的实体约束语言,其一阶逻辑表达式如下:
φ:∀Tα,Tβ,Tγ,…∈R,(p1∧p2∧…∧pm)
其中,R是关系模式,Tx是任一元组,x∈{α,β,γ,…},pi是否定约束所包含的谓词表达式,其形式是ν1φν2或者ν1φc,ν1,ν2∈Tx.A,A是任一属性,φ是谓词表达式所包含的关系运算符,包括{=,≠,>,<},c是常量.

3.2 符合度计算
如果一对元组不符合给定的否定约束φ,称该元组对为冲突元组对,反之为无冲突元组对.否定约束对数据集的符合程度,既与冲突元组集对其的负支持度有关,又与无冲突元组集对其的正支持度有关.接下来将分别引入负支持度和正支持度这两个质量维度的概念.
3.2.1 负支持度
设一个否定约束φ包含的谓词表达式个数为|φ.predicates|,根据φ所表达的约束语义,如果一对元组满足的谓词表达式个数为|φ.predicates|,则该对元组存在冲突.冲突元组集对否定约束的支持度既与φ所包含的谓词表达式个数有关,又与违反φ的冲突元组对的数量有关.|φ.predicates|越大,则表明φ中假设的谓词表达式越多,从而导致否定约束的各谓词表达式之间可能存在冗余问题.另外,待测数据集的正确元组数往往远大于错误元组数,如果违反φ的元组对数较多,则表明φ对数据集的符合度程度较小.将否定约束形成的字母表标识为L={Tα,Tβ,A,OP,C},其中Tα,Tβ为一对元组,A是所有属性的集合,OP是算术运算符和逻辑运算符的集合,C是常量,Len(φ)为L中出现在φ中的不同元素个数,如(Tα.SL<5000)包含、Tα、SL、<和5000这五种不同元素,故其Len(φ)=5.因违反同一否定约束φ的冲突元组对可能有多个,所以将冲突元组集对给定否定约束的违反度定义为:
(1)
其中,kcp是违反φ的元组对数,|V|表示违反φ的冲突元组数,可得冲突元组集对φ的负支持度表达式为:
NS(φ)=1-Denial(φ)
(2)
例1.以表1中的税务记录为例,每条记录描述具有7个属性的个人地址和税务信息:姓名(NE),区号(AC),城市(CT),区(DT),邮编(ZIP),工资(SL),税率(TR).
表1 税务数据记录
Table 1 Tax data record

TIDNEACCTDTZIPSLTRT1刘德010北京朝阳区10000050003T2陈超021上海黄浦区200001600004.6T3盎司010北京东城区10000050003T4陈敏022天津和平区300000850007.2T5赵军023重庆万州区404100150002.4T6李伟021上海闵行区201100600004.5T7王宝024沈阳和平区110001700007T8张丽010南京崇文区100000100004T9孙强010北京丰台区10000050003T10李帅020广州黄埔区510700400006
假设存在以下否定约束:
c1:(Tα.ZIP=Tβ.ZIP∧Tα.CT≠Tβ.CT)
c2:(Tα.AC=Tβ.AC∧Tα.CT≠Tβ.CT)
c3:(Tα.CT=Tβ.CT∧Tα.SL
c4:(Tα.CT=Tβ.CT∧Tα.SL=Tβ.SL∧Tα.TR≠Tβ.TR)
c5:(Tα.ZIP=Tβ.ZIP∧Tα.SL
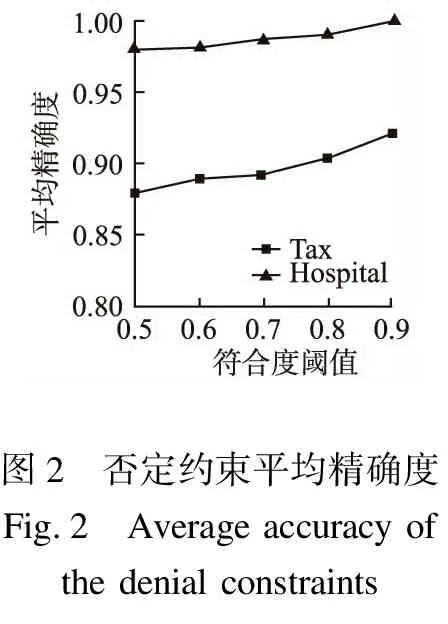
c6:(Tα.CT=Tβ.CT∧Tα.SL>Tβ.SL∧Tα.TR 考虑例1中的数据集及给定的否定约束c1和c4,其中,|c1.predicates|=2,Len(c1)=8,违反c1的元组对为〈T1,T8〉,〈T3,T8〉和〈T8,T9〉,所涉及的冲突元组为T1,T3,T8和T9,即kcp=3,|V|=4,可得NS(c1)=0.8125.|c4.predicates|=3,Len(c4)=9,违反c4的元组对为〈T2,T6〉,即kcp=1,|V|=2,可得NS(c4)=0.8333. 如果仅考虑负支持度,由计算结果可知c4对数据集的符合程度优于c1,但通常情况下,无冲突元组对的数量要远大于冲突元组对的数量,所以必须考虑无冲突元组集对给定否定约束的正支持度.接下来引入正支持度的概念. 3.2.2 正支持度 一个否定约束φ能够成立的证据是存在不违反φ的元组对,即无冲突元组对.满足φ的无冲突元组对往往不唯一,但匹配φ中的谓词表达式个数可能不同,因此我们将满足k个谓词表达式的元组对称为k-Evidence,简写为kE.kE中满足的谓词表达式数越多,它对φ的支持度就越大.为了反映这一特性,我们为kE引入一个权重w(k),其值从0到1变化,并且随k的增大而增大,表达式如下: (3) 基于这样的证据,将无冲突元组集对φ的正支持度表达式PS(φ)定义为: (4) 其中,|kE|是各类证据所对应的无冲突元组对个数,k=0,1,…,|φ.predicates|-1. 如果仅考虑正支持度,由计算结果可知c1对数据集符合程度优于c4,这与仅考虑负支持度的计算结果相反,所以必须综合考虑正、负支持度这两个质量维度,为此我们接下来引入符合度记分函数的概念. 3.2.3 符合度记分函数 否定约束对数据集的符合程度既与负支持度有关,又与正支持度有关,仅考虑一种支持度具有片面性.为了准确计算出否定约束对数据集的符合程度,我们引入记分函数来计算每个否定约束的符合度分数.对于给定的φ,将符合度记分函数定义为两个质量维度的线性加权组合. Conf(φ)=α*PS(φ)+(1-α)*NS(φ) (5) 其中,Conf(φ)在0到1之间取值,值越大,表明φ对数据集的符合程度越好.α是两个质量维度的平衡因子,其值在0到1之间,表示无冲突元组对在给定数据集的所有元组对中所占的比例,即正支持度的比例因子,则1-α就为负支持度的比例因子,α的表达式定义如下: (6) 通过引入平衡因子α可以消除仅考虑一种支持度的片面性,使符合度的计算结果更准确. 为提高否定约束对数据集的符合程度,我们使用Conf(φ)计算每个否定约束的符合度分数,并与符合度阈值λ进行比较,剔除小于λ的否定约束,从而得到满足符合度阈值的否定约束集Σλ.算法1是否定约束符合度校准算法. 算法1.否定约束符合度校准算法. 输入:数据实例I,待测否定约束集Σ,符合度阈值λ 输出:满足符合度阈值的否定约束集Σλ 1.Σλ的初值是待测否定约束集Σ; 2.for eachφin Σ 3.for each 〈Tα,Tβ〉 inI 4. while(k≤|φ.predicates|) 5. if(k=|φ.predicates|) 6.φ的冲突元组对数加1; 7. 统计φ对应的各类证据个数,并计算出证据总数; 8. 由公式(3)计算各类证据对应的权重; 9.k++; 10.由公式(1)、(2)求出φ的负支持度分数NS(φ); 11.由公式(4)求出φ的正支持度分数PS(φ); 12.由公式(6)求出平衡因子α的值; 13.由公式(5)求出φ的符合度分数Conf(φ); 14.if(Conf(φ)<λ) 15. Σλ=Σλ-φ; 16.return Σλ; 其中k表示元组对〈Tα,Tβ〉满足φ所包含的谓词表达式个数,初值为0.通过算法1我们得到了满足符合度阈值的否定约束集. 定义2.对称冲突是指作用于同一组属性上的两个否定约束,其所包含的谓词表达式相同或相反. 定义3.冗余冲突是指给定两个或多个否定约束,其中某个否定约束可由其它否定约束推导得出. 本文考虑的谓词表达式包含{=,≠,>,<}这四种运算符,每个否定约束包含不同的谓词表达式.为了便于分析否定约束之间存在的冲突,我们用{1,-1,2,-2}这四个关联因子分别对应四种运算符所构成的谓词表达式,则否定约束所包含的谓词表达式可以通过一个关联矩阵来表示.我们用行标代表各否定约束,列标代表各元组属性,0代表否定约束与属性之间没有约束关系.算法2为关联矩阵构建算法. 算法2.关联矩阵构建算法. 输入:满足符合度阈值的否定约束集Σλ,元组属性集ΣA 输出:关联矩阵Matrix(Σλ,ΣA) 1.for eachφin Σλ 2.for eachAin ΣA 3. if(Ainφ) 4. if(Tα.A=Tβ.Ainφ) 5.Matrix(Σλ,ΣA)中属性A所对应的位置为1; 6. else if(Tα.A≠Tβ.Ainφ) 7.Matrix(Σλ,ΣA)中属性A所对应的位置为-1; 8. else if(Tα.A>Tβ.Ainφ) 9.Matrix(Σλ,ΣA)中属性A所对应的位置为2; 10. else if(Tα.A 11.Matrix(Σλ,ΣA)中属性A所对应的位置为-2; 12. else 13.Matrix(Σλ,ΣA)中属性A所对应的位置为0; 14.returnMatrix(Σλ,ΣA); 其中Tα,Tβ是否定约束中谓词表达式所包含的元组,A是任一属性.考虑例1中给出的否定约束,其对应的关联矩阵如下: 对例1中的否定约束进行分析可得,c3和c6只有一个谓词表达式相同,其余均相反,两约束之间存在对称冲突;c5表达的语义与c1和c3共同表达的语义相同,三个约束之间出现了冗余冲突.作用于同一数据集的否定约束数量往往比较大,少则几十个,多则几百个.不论出现以上哪种情况,都会影响数据清洗质量,因此,必须采用有效的机制,在对数据进行清洗之前,先消除否定约束之间可能存在的冲突,以提高否定约束的精确度. 基于符合度记分函数和关联矩阵的分析,我们设计出算法3对否定约束集进行校准. 算法3.否定约束集校准算法. 输入:关联矩阵Matrix(Σλ,ΣA) 输出:校准否定约束集Σ′ 1.Σ′的初值为满足符合度阈值的否定约束集Σλ; 2.for eachφi,φjinMatrix(Σλ,ΣA) 3. if (φi,φjsatisfy 对称冲突) 4. 删除φi,φj中符合度分数较低的那一个; 5. if (φi⊃φj) 6. 删除φj; 7.for eachφi,φj,φkinMatrix(Σλ,ΣA) 8. if (φi+φj⊃φk) 9. 删除φk; 10.return Σ′; 通过算法3我们得到了校准否定约束集,下面可以利用它进行数据检测与修复. 证据规则是指在数据检测过程中发现冲突元组对的否定约束.数据检测阶段是针对算法3返回的校准否定约束集,检测出其中的证据规则集Σe及对应的冲突元组集Tc.算法4是数据检测算法. 算法4.数据检测算法. 输入:数据实例I,校准否定约束集Σ′ 输出:证据规则集Σe,冲突元组集Tc 1.Σe,Tc的初值均为空; 2.for eachφin Σ′ 3.for each 〈Tα,Tβ〉 inI 4. if (〈Tα,Tβ〉 satisfyφ.predicates) 5.φ添加到Σe中; 6. 〈Tα,Tβ〉添加到φ对应的冲突元组集Tc中; 7. 记录φ冲突元组对数的指针加1; 8.return Σe,Tc; 其中,φ.predicates表示φ中的谓词表达式集.通过算法4我们得到了证据规则集及对应的冲突元组集,接下来对原始数据集进行修复. 定义4.条件概率是指在同一个样本空间Ω中的事件或者子集A与B,如果随机从Ω中选出的一个元素属于A,那么下一个随机选择的元素属于B的概率.其表达式如下: (7) 数据修复阶段是针对算法4返回的证据规则集Σe,修复其对应的冲突元组集Tc,但不同的证据规则选取顺序可能产生不同的修复结果.因此,我们根据每个证据规则的符合度分数,从高到低修复检测出的冲突元组集,直到每个否定约束都没有对应的冲突元组集.每个冲突属性的候选取值可能有多个,我们总是选取使条件概率达到最大值的属性值作为冲突属性的修复值.算法5是冲突元组修复算法. 算法5.冲突元组修复算法. 输入:数据实例I,证据规则集Σe,冲突元组集Tc 输出:修复结果I′ 1.repeat 2.for eachφin Σe 3. 根据Conf(φ),从高到低选取φ及对应的Tc; 4. for each conflictAinTc 5. 统计A取每一个可能值的个数及所有可能值的总数; 6. 由公式(7)求出A取每一个可能值的条件概率P; 7. 选取P最大的属性值作为A的修复值; 8.until(Σe=φ); 实验运行在使用Intel酷睿i5-2.5GHz的CPU,4GB内存,64位Windows 10操作系统的计算机上.本文使用文献[15]中的税务数据Tax作为模拟数据集,每条记录描述具有15个属性的个人地址和税务信息,使用从Web数据源[注]http://data.medicare.gov/data/hospital-compare获取的由美国政府统计的,包含160k条记录的Hospital数据作为真实数据集. 实验假定所选取的数据集都是正确的,通过某种错误率e人为地引入噪声数据. 5.2.1 符合度阈值λ的确定 λ的选取对否定约束的检测精确度具有较大影响.取值太小,满足条件的否定约束就比较多,从而可能引入无效的否定约束,取值太大,满足条件的否定约束又比较少,从而可能丢失符合条件的否定约束.λ的取值与α紧密相关,由公式(5)和公式(6)可知0.5≤λ≤1.实验使用平均精确度这一指标来确定λ的取值,将平均精确度定义为满足λ的否定约束中真实成立的否定约束所占的比例. 图2显示了λ取不同值时否定约束检测的平均精确度,从图中可以看出: 1)平均精确度随着λ的增大而增大,且增幅波动较小.这是因为λ取值越大,返回的否定约束就越少,而真实成立的否定约束相对增多,所以平均精确度随着λ的增大而增大. 2)当λ=0.9时,平均精确度达到最优,但这只是局部最优,并不能将λ的值设定为0.9.因为λ值越小,候选的否定约束数量就越多,可能冲突的否定约束数量也随之增多,致使所求比例的分子相对减小,所以平均精确度随λ的减小而降低.但只要平均精确度大于0,就说明可能存在真实成立的否定约束,而否定约束精确度检测实验中要引入噪声数据,可能会降低部分否定约束的符合度分数,为避免丢失符合条件的否定约束,本文选取λ=0.5. 图2 否定约束平均精确度Fig.2 Average accuracy of the denial constraints 5.2.2 约束规则检测精确度评估 实验使用精确度这一指标来评估DR-RDC对约束规则的检测效果.同时,为了在相同条件下比较DR-RDC与最新研究文献[11]采用的数据语义置信度(Data Semantic Confidence,简称DSC)方法,我们使用文献[16]中提出的函数依赖挖掘算法得到待测函数依赖集,这保证了DR-RDC和DSC方法针对同一约束规则集进行检测.基于top-k算法的思想,将精确度定义为返回的前k(实验中按照百分比计算)个候选中真实成立的函数依赖所占的比例.图3是DR-RDC与DSC的实验效果对比分析图. 图3 DR-RDC与DSC精确度对比分析Fig.3 Comparison between DR-RDC and DSC in accuracy 从图中可以得到: 1)不同错误率下,DR-RDC的检测精确度明显优于DSC,且DSC情况下函数依赖的检测精确度波动比较大.这是因为DR-RDC既考虑了函数依赖对数据集的符合程度,又考虑了函数依赖之间可能存在的冲突,其计算精确度的针对目标是所有满足符合度阈值λ的函数依赖,根据函数依赖之间的冲突数量来判断检测精确度,而DSC只考虑函数依赖置信度的大小,其计算精确度的针对目标是所有函数依赖,且仅根据置信度的大小来判断函数依赖的检测精确度.这既可能引入无效的函数依赖,又可能丢失成立的函数依赖,所以精确度的检测结果波动比较大. 2)当横坐标的取值大于0.6时,DSC情况下横纵坐标的乘积在减小.这是因为当横坐标取值为0.6时,DSC方法已经挖掘了所有满足置信度阈值的函数依赖,在余下的部分没有满足条件的函数依赖,所以横纵坐标的乘积在逐渐减小.由实验结果可得,DR-RDC优于DSC. 5.2.3 数据检测与修复效果评估 为验证我们算法所得的校准否定约束集对数据修复的性能,本文使用错误检测率和错误修复率这两个指标对DR-RDC方法和使用原始否定约束集的数据修复效果进行对比分析.错误检测率Dr和修复率Rr的表达式定义如下: (8) (9) 图4是DR-RDC与原始否定约束集的实验效果对比分析图. 图4 DR-RDC与原始否定约束集对比分析Fig.4 Comparison between DR-RDC and raw denial constraint sets 图4中x轴表示数据集中噪声数据的比例,y轴是对应的检测指标.从图4可以看出: 1)DR-RDC对数据集的错误检测率和修复率均在90%上,这说明本文所提出的方法具有显著的清洗效果. 2)相同条件下,原始否定约束集对数据集的错误检测率整体上略高于DR-RDC的实验结果,但错误修复率明显低于DR-RDC的实验结果,且原始否定约束集对数据集的错误检测率和修复率相差较大.这是因为原始否定约束集未考虑其对数据集的符合程度,及否定约束之间可能存在的冲突,致使原始否定约束集中包含一些无效的否定约束,在对数据集进行检测时,会将一些正确的数据误判为错误数据,导致其错误检测率偏高,而数据修复过程中,可能将原本正确的数据修改为错误数据,导致其错误修复率降低,所以产生错误检测率与修复率相差较大的结果. 综上分析可得,本文提出的DR-RDC方法正确可行,能够有效的解决数据中的不一致问题,且相对于原始约束规则,数据修复效果有显著的提升. 数据质量规则是解决数据不一致问题的有效方法,然而含冲突的、符合度较低的约束规则却会极大的降低数据清洗效果.本文首先利用符合度记分函数和关联矩阵对否定约束集进行校准,得出高符合度的校准否定约束集,将其作用于待测数据集,得出证据规则集及对应的冲突元组集,根据证据规则的符合度分数,从高到低地修复其对应的冲突元组集,选取使条件概率最大的属性值作为冲突属性修复值,直到冲突元组集不违反任一否定约束.通过实验验证了DR-RDC方法的可行性和高效性.未来的工作中,我们将致力于提高符合度阈值λ准确度的同时优化算法,进一步提高约束规则的检测精确度,提升数据修复的质量和效率.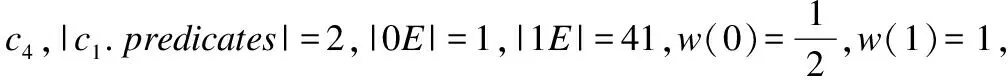
3.3 校准步骤1:符合度校准
3.4 校准步骤2:冲突消除

4 数据检测与修复
4.1 数据检测
4.2 数据修复
5 实验及结果
5.1 实验配置与数据集
5.2 实验结果及分析


6 总结与展望

