基于典型工况的电力推进系统优化设计

熊留青， 高海波， 郑锐聪， 卢炳岐， 杜康立

(1. 武汉理工大学 能源与动力工程学院， 武汉 430063；2. 广州海工船舶设备有限公司， 广州 511495)

船舶动力系统是船舶的“心脏”，直接关系到船舶的主要性能，寻求优化的动力系统设计方法是船舶设计的热点。[1-2]系统设备的选型受多方面的制约，普通的设计方法很难选定设备的最佳型号，许多学者探讨将智能优化算法应用在船舶设计中。常用的智能优化算法是将多目标问题转化为单目标问题求解，事先设定偏好信息，因此将不可避免地遗漏更好的可行解。[3]

针对上述问题，部分学者尝试将多目标优化算法和智能优化算法相结合。文献[4]提出基于Pareto占优的多目标粒子群算法来优化船舶主尺度的设计。文献[5]采用非支配排序遗传算法优化混合动力系统的选型设计。文献[6]系统地研究5种智能优化算法，并将其应用于船舶设计过程中的3类不同问题。文献[7]将多目标粒子群算法和其他几种典型的多目标优化算法进行对比分析。但面向典型工况的智能优化设计方法还鲜有文献论述。

本文根据广州海工船舶设备有限公司诱鱼艇的典型工况，为其设计电力推进系统方案，提出以阈值法为核心的能量管理策略，在选型优化设计中引入多目标粒子群优化(Multi-Objective Particle Swarm Optimization, MOPSO)算法，并对其加以改进，运用逼近理想解的排序方法对Pareto非劣解集做出排序，达到辅助决策的目的。

1 诱鱼艇动力系统结构设计

以广州海工船舶设备有限公司生产的诱鱼艇为研究对象，其采用柴油发电机组供电给电机推进船舶，艇体尺寸为8.0 m×2.4 m×1.5 m，排水量为4.6 t，柴油发电机组功率为70 kW，电机功率为40 kW，经济航速为8 kn，最高航速为10 kn。

根据诱鱼艇典型作业工况数据，可得到一个作业周期内的柴油发电机组功率图谱(见图1)。诱鱼艇共有3种作业模式。

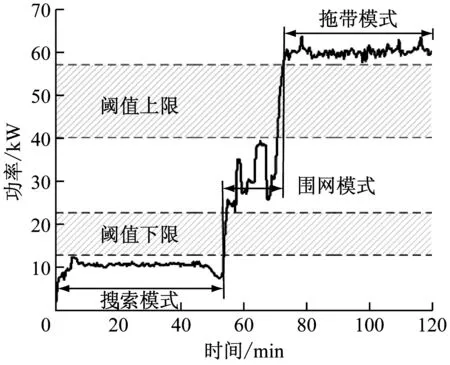
图1 诱鱼艇1个作业周期内柴发机组功率图谱

1) 第一阶段为搜索模式，渔船到达渔场后放下诱鱼艇，诱鱼艇微速搜索鱼群，探测到鱼群后开启诱鱼灯，当诱集到足够鱼群后，逐渐靠近主船，同时调暗灯光，此过程约60 min，功率需求约为10 kW。

2) 第二阶段为围网模式，诱鱼艇在网圈内控制鱼群，拖带网头，调整网形，这一阶段工况复杂多变，约20 min，功率需求为20～40 kW。

3) 第三阶段为拖带模式，诱鱼艇拖带网船或运输船，使之保持一定距离，此过程大约40 min，功率需求约为60 kW。[8]

从图1可知：诱鱼艇作业模式相对固定，在搜索模式和围网模式下，柴油机负荷较低，偏离最佳工况点，油耗率高，排放特性差。本文为诱鱼艇设计一种电力推进系统方案，并提出一种智能优化设计方法为系统进行优化选型(见图2)。该方案采用柴油发电机组为主、蓄电池组为辅的供电方式，以变频器直流母线作为公共母线。蓄电池组不仅可作为能量源，还可作为储能装置，从而使柴油机发电机组始终运行在最佳工况点附近，既能延长其使用寿命，减少柴电机组装机容量，又能达到节能减排降噪的效果。[9-10]

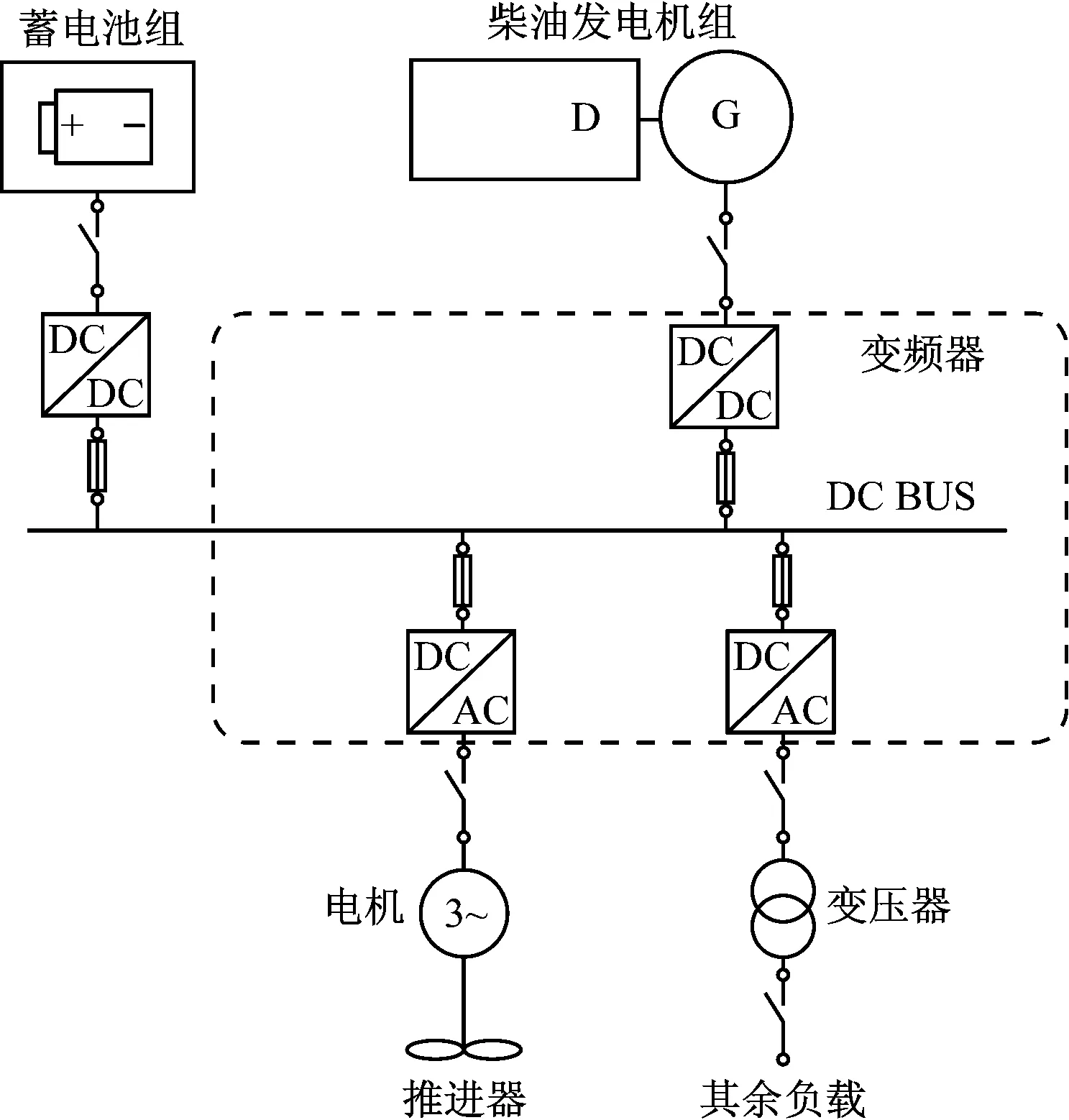
图2 电力推进系统方案结构

2 动力系统能量管理策略

能量管理策略是本文所设计的电力推进系统方案的关键技术之一，从技术难点和开发成本的角度来考虑，选用基于阈值法的能量管理策略。[11-12]能量管理系统通过监测船舶需求功率和蓄电池荷电状态(State Of Charge, SOC)，从而自动切换工作模式，调整柴油发电机组和蓄电池组的工作状态。本文根据诱鱼艇的典型工况设计4种供电模式。

1) 模式一为蓄电池组通过DC/DC变换器为变频器和推进电机及其他辅助负载供电，柴油发电机组不工作。

2) 模式二为柴油发电机组供电，同时通过变频器的直流母线，经DC/DC变换器为蓄电池组充电。

3) 模式三为柴油发电机组单独供电。

4) 模式四为柴油发电机组和蓄电池组联合供电。

能量管理策略的输入是实际负载需求Pload以及电池SOC值，输出为柴油发电机组输出功率Pd、蓄电池组放电功率Pb_dis以及充电功率Pb_char。阈值控制规则见表1，其制定原则是合理分配柴油发电机组的输出功率和蓄电池组的充放电功率，使柴油发电机组始终运行在最佳工况点附近。Pmax、Pmin分别为设定的柴油发电机组功率阈值上限和下限，本设计中Pmax、Pmin分别为柴油发电机组100%和40%的额定功率，其阈值上下限应处于模式之间的过渡阶段见表1。

3 诱鱼艇动力系统仿真设计

从系统成本、设备质量和燃油消耗多角度综合考虑设备选型问题，其中燃油消耗量的计算涉及到实际工况，因此，在MATLAB/SIMULINK中搭建系统能量管理模型、蓄电池充放电模型、油耗模型等来模拟诱鱼艇一个工作周期内的实际油耗。[13-14]

表1 阈值控制规则表

电力推进系统仿真模型见图3，主要由能量管理系统模型、油耗模型和蓄电池组充放电模型等3部分组成。能量管理系统模型根据表1，由负荷需求和蓄电池SOC值选择供电模式，同时通过设置relay模块避免蓄电池组SOC值较低时连续地充放电，relay模块相当于滞环比较器，设置开关开启设定值45%，输出值60%，开关关闭设定值40%，输出值30%，能量管理系统仿真模型见图4。

1) 当relay模块输出60%时，表示蓄电池组不处于低电量状态，既可充电又可放电。

2) 当relay模块输出30%时，表示蓄电池组处于低电量状态，此时只能充电。

3) 当充电到45%时，relay模块开启开关，输出60%，此时可充电可放电。

4) 当放电到40%时，关闭开关，输出30%，此时只能充电。避免了蓄电池组SOC值在40%左右连续地充放电。油耗模型根据柴油发电组额定功率及负荷百分比插值得出油耗速率，再通过积分运算得出一个工作周期内的柴油机燃油消耗量，其计算结果作为选型目标之一，油耗仿真模型见图5。蓄电池组充放电通过对双向DC/DC的控制来实现蓄电池组的充放电，其仿真模型见图6。

图3 电力推进系统仿真模型

4 诱鱼艇动力系统设备选型设计

4.1 选型方法优化设计

针对电力推进系统方案主要设备优化选型问题，利用MOPSO算法求解出成本、质量、油耗及排放目标下的Pareto最优解集。在MOPSO算法中，粒子群在超微空间搜索Pareto解集[15-16]，粒子在空间飞行的速度和位置更新公式为

图4 能量管理系统仿真模型图5 油耗仿真模型

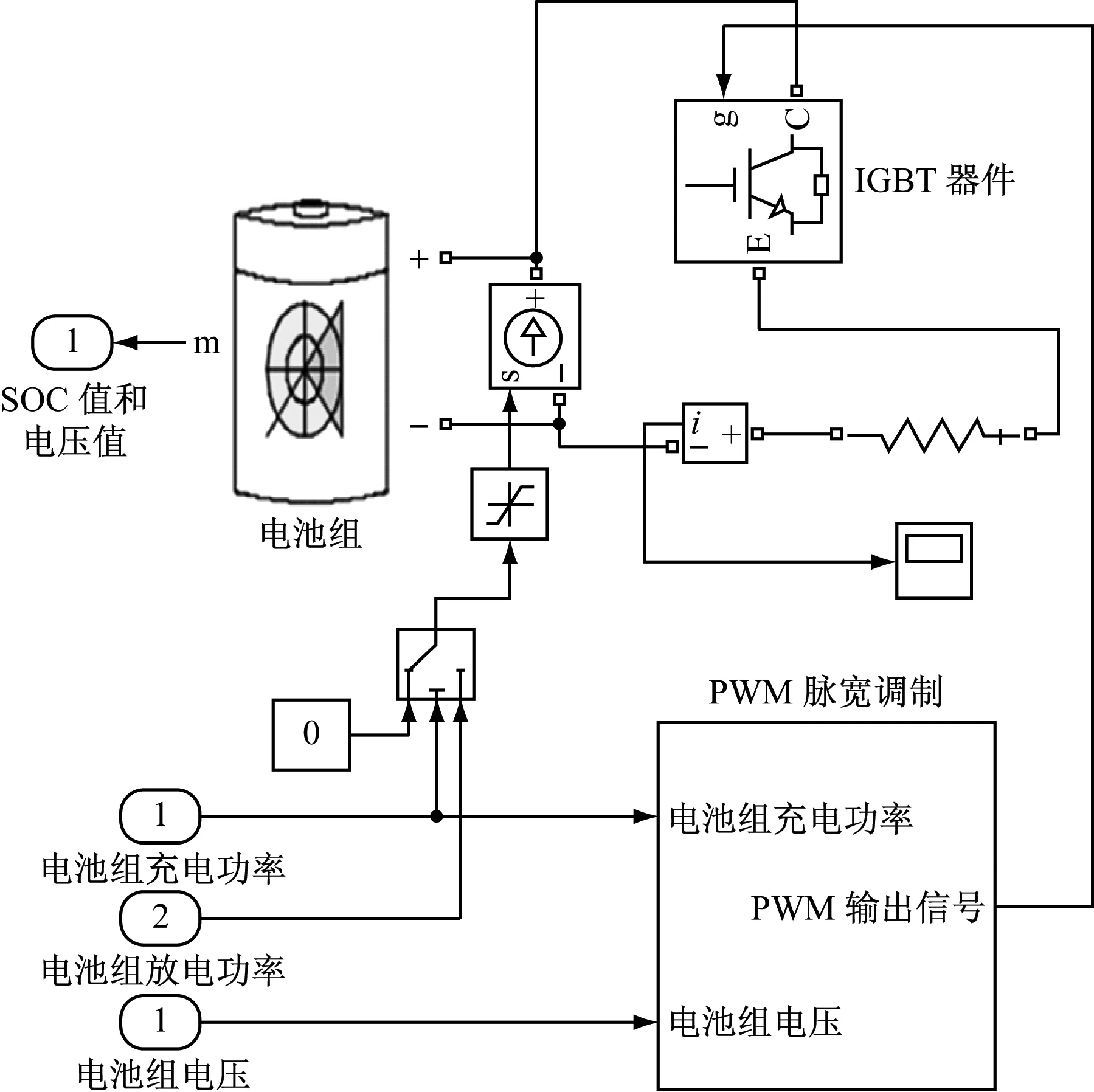
图6 蓄电池充放电仿真模型

vi(t+1)=w×vi(t)+C1×r1(pi-xi(t))+

C2×r2(pg-xi(t))

(1)

xi(t+1)=xi(t)+vi(t+1)

(2)

式(1)和式(2)中：pi和pg分别为个体极值和全局极值；vi(t)和vi(t+1)分别为第t次迭代和第t+1次迭代时的粒子速度；xi(t)和xi(t+1)分别为第t次迭代和第t+1次迭代时的粒子位置；w为惯性因子；C1和C2为认知学习因子和社会学习因子，r1,r2∈[0, 1]，是服从均匀分布的随机变量。

在MOPSO评价和非劣解选择阶段，引入非支配排序评价思想和循环拥挤距离思想。

1) 非支配排序评价思想是根据多目标函数值，将所有不被其余解支配的解作为前沿1，在剩余解中将所有不被其余解支配的解作为前沿2，重复上述操作，直至得到所有的非支配解。

2) 循环拥挤距离思想是当非支配解的总数量大于所规定的数量时，对该前沿上的解计算拥挤距离，并剔除拥挤距离最小的解，再对该前沿上剩余的解计算拥挤距离，并剔除拥挤距离最小的解，重复上述操作，直至所剩的解正好能满足所要求的数量。

MOPSO算法收敛速度快，调试参数少，在优化前期容易向最优值靠近，但因缺乏种群多样性而在最优值附近收敛速度较慢。针对该问题提出多目标动态惯性权重的概念，定义多目标动态惯性权重的计算式为

(3)

wt=eαt/αt-1

(4)

式(4)中：N为粒子个数；n为目标个数；fj(xt，i)为第t次迭代时第i个粒子的第j个目标函数值；fj(xt，min)为第t次迭代时最优粒子的第j个目标函数值，fk(xt，min)为第t次迭代时最优粒子的第k个目标函数值；αt和αt-1分别为第t次和第t-1次迭代粒子群平均加权距离；wt为第t次迭代时惯性因子。

为避免算法早熟，将混沌运动引入到MOPSO算法中，即混沌初始化和全局极值混沌干扰。利用混沌运动的遍历性，根据粒子间欧氏距离，从中提取大量分布均匀的初始粒子，构成初始种群，在进化过程中对粒子的全局极值进行混沌局部搜索，从而提高MOPSO算法的寻优能力。改进后的MOPSO算法为

1) 混沌初始化。随机产生一个D维向量z，然后根据式(5)的Logistic方程得到n个分量z1,z2, …,zn，构成混沌区间，各分量取值范围为[0,1]。再根据式(6)将混沌区间映射到优化变量的取值范围，构成初始粒子种群。

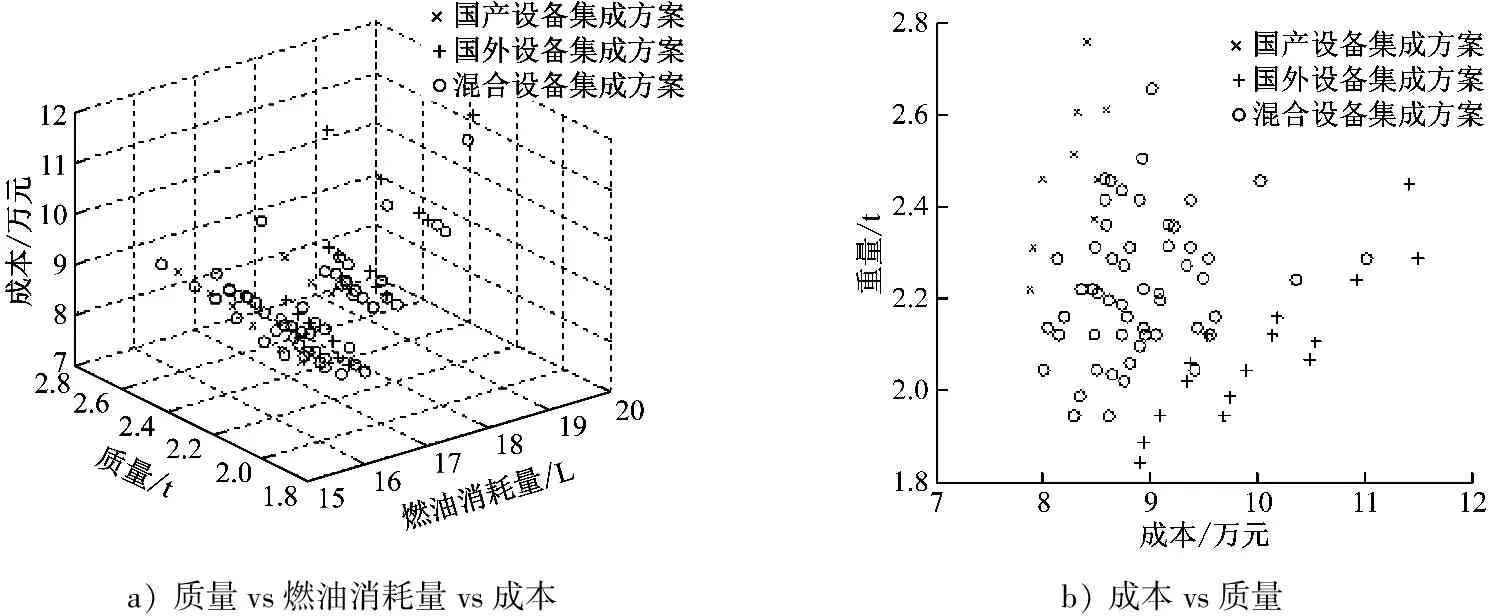
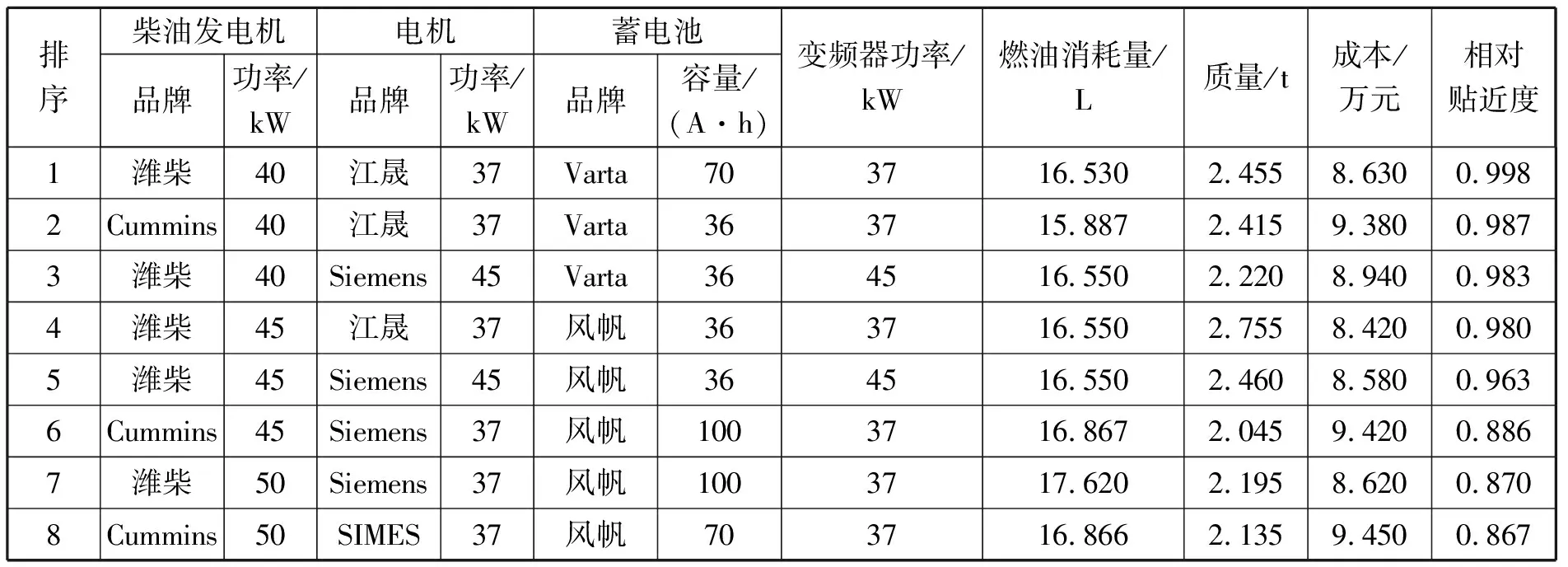
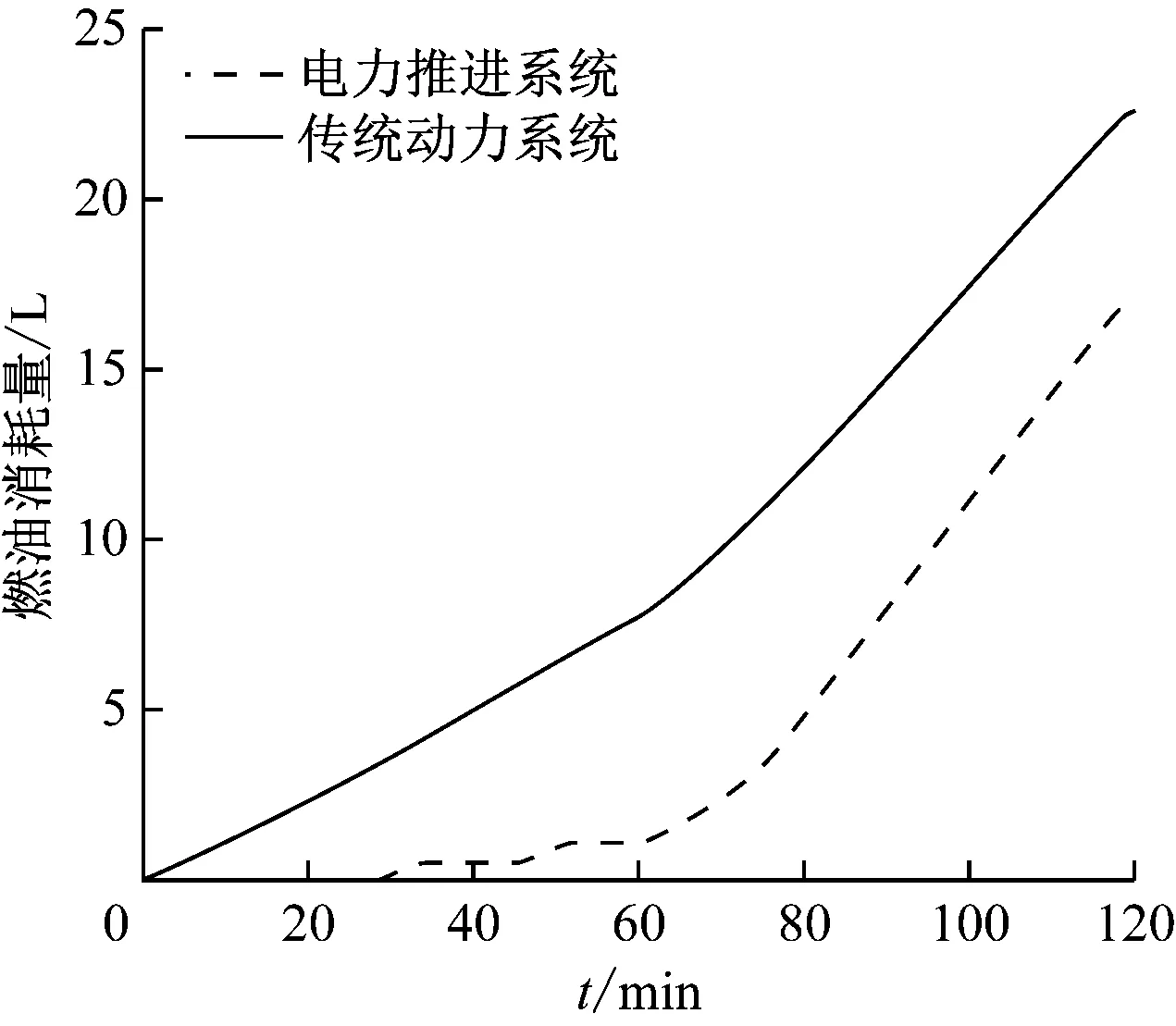
zn+1=μzn1-zn，n=0,1,2,…;0

μ∈0,4

(5)

xij=aj+bj-ajzij，i=1,2,…,N;j=1,2,…,D

(6)

式(5)和式(6)中：bj和aj分别为优化变量的上下限。

2) 初始个体极值和全局极值。定义粒子当前位置为个体极值Pi，随机产生初始粒子群的速度，采用非支配评价思想得到第1代解集，随机选取其中一个解，定义为全局极值Pg。

3) 种群迭代。根据式(1)和式(2)更新粒子群的速度和位置，将更新后的粒子群与当代解集组合，采用非支配评价以及循环拥挤距离思想，得到当代解集以及当代个体极值Pi和全局极值Pg。

(7)

5) 返回步骤3)，直到迭代次数结束或满足终止条件，输出计算结果。

4.2 决策方法设计

设备优化选型涉及多目标决策问题，采用上节所述的智能优化算法可得到一系列可行的选型方案，但最终的方案仍由决策者决定。本文引入逼近理想解排序方法(Technique for Order Preference by Similarity to an Ideal Solution, TOPSIS)作为决策方法，根据评价目标与理想目标之间的接近程度来进行排序，能够科学地辅助决策者做出选择。

TOPSIS算法的评价目标为Pareto选型方案解集, 理想目标分为正理想解和负理想解，其取值应根据决策者对多目标的要求来选取。设定评价目标为Si，正理想解为S+，负理想解为S-。

(8)

(9)

(10)

式(8)和式(9)分别为评价目标Si与正负理想解之间的距离，记为di+和di—；式(10)为方案Si相对贴近度Ci的计算公式，Ci值越大表示评价目标Si越接近正理想解，更符合决策者的要求。

5 案例分析

为保持选型样本的多样性和合理性，以国内外品牌知名度较高的设备为选型对象，选用40 kW、45 kW、50 kW和55 kW的国外Cummins与国产潍柴柴油发电机组各一组，12 V/36 A·h、12 V/70 A·h和12 V/100 A·h的国外Varta和国内风帆蓄电池各一组，37 kW、45 kW和55 kW的国外Siemens和国产江晟电机各一组，以及适配电机功率的37 kW、45 kW和55 kW的英威腾变频器作为研究对象，即选型优化变量。

选择系统成本、设备质量和燃油消耗量作为选型优化目标，设置MOPSO空间维数为3，混沌初始化粒子数量为50，最大迭代次数为100，惯性权重初始值为0.4，学习认知因子C1为2.0，社会认知因子C2为2.0，计算精度为0.001。结合系统油耗模型以及改进的MOPSO算法，得到79个Pareto最优解，MOPSO优化选型Pareto解集分布见图7。

由图7a可知：Pareto解集分布是比较均匀的，国外设备集成方案指电力推进系统集成时全采用国外设备，国产设备集成方案指系统集成时全采用国产设备，混合设备集成方案指国外设备和国产设备均有采用。理论上来说，这79个解都可作为选型方案，决策者拥有很大的选择空间。由图7b可知：国产设备集成方案分布于左上角，国外设备集成方案分布于右下角，混合设备集成方案居中，说明国产设备较国外设备成本较低，质量较大。由图7c可知：在柴油发电机组功率等级差不多的情况下，国产设备集成方案油耗较高，成本较低。由图7d)可知：国产设备集成方案重量较大，油耗较高。Pareto最优解集的分布符合实际情况，同时也说明寻优结果合理可信。

本文研究中系统成本为首要考虑因素，燃油消耗为第2考虑因素，设备质量只要在合理范围内即可。采用TOPSIS排序方法对图7中的Pareto最优解集排序，根据相对贴近度依次选取前8种方案，设置典型工况下正理想解为燃油消耗量17 L，质量为2.6 t，成本8万元，负理想解为燃油消耗量19.5 L，质量3.0 t，成本11.5万元。得到的TOPSIS排序结果见表2。选取表2中第1个方案作为最终优选方案，由图7可知：该方案燃油消耗量及成本较低，质量虽然较大，但仍可接受，符合设计要求。本文是从设计者的角度出发给出最终方案，实际决策过程中，不同用户可能产生不同的满意解。

本文根据典型工况下的如图5所示的油耗仿真模型来验证电力推进系统优化方案的节能效果，改进前后油耗对比见图8，初始时蓄电池SOC值为100%，所储电能折算为油耗约8 L，终止时SOC值为60%，折合燃油量约4.2 L，则一个工作周期内，电力推进优化方案比传统方案节省了9.3%的油耗，节能效果显著。

a) 质量vs燃油消耗量vs成本b) 成本vs质量

c) 成本vs燃油消耗量d) 质量vs燃油消耗量

图7 MOPSO优化选型Pareto解集分布图

图8 改进前后油耗对比图

6 结束语

本文提出基于多目标惯性权重和混沌运动的MOPSO算法，应用在广州海工诱鱼艇电力推进系统优化设计中，引入TOPSIS排序方法为用户的科学决策提供支持。仿真结果表明：采用智能优化算法设计出的电力推进方案能达到节能减排的效果。本文的研究为船舶电力推进系统设计提供了一种新的设计算法及决策方法和实船案例，具有一定的推广价值。