基于四维离散数值方法的岩石圆环试样动态破坏及耗能规律

张奔，赵高峰

(天津大学 建筑工程学院，天津 300072)

近年来,地下空间不断得到新的拓展和开发，许多重大基础设施,如地铁、人防工程、核废料处置库等在地下相继修建。长期以来，人们对地下工程的抗震性能都持较为乐观的态度，认为地下工程抗震能力要远优于地上结构，然而，最近一些地震活动导致的地下工程严重破坏乃至坍塌的案例[1]使人们开始对地下工程在地震作用下的稳定性进行更深入的研究。与地面建筑以抗震设计为主不同，地下重大基础设施多采用更为有效的隔震手段[2]。地震属于振动形式的一种，隔振技术主要通过有效的防护措施将建筑物和振动环境进行适当隔离，通过降低能量的输入保证建筑结构在载荷冲击过程中尽量保持正常状态[3]。实际工程中,常采用在重要地下硐室旁开挖辅助硐室的方式来隔离动力灾害，通过钻孔的方式来改变岩体的动力学阻抗也是一种可行的隔震方式。

作为一种新型多功能材料,孔隙材料在能量吸收方面展现了良好的性能[4-8]，近年来备受关注。其中，类岩石孔隙材料由于质量轻、耗能好、耐久性高等特点而被用于土建工程中，其吸能减振的机理受到了科研工作者的广泛重视。王智等[9]对多孔混凝土的制备方法进行探究，在保证孔隙率的条件下有效提高了混凝土的强度。黄胜等[10]、赵武胜等[11]将自制的泡沫混凝土作为西藏扎墨公路嘎隆拉隧道的隔震层进行模拟计算，破坏区的范围得到有效缩小，证明了孔隙材料保护隧道免遭地震波冲击的良好性能。王代华等[12]对含有泡沫混凝土层的复合结构在爆破中的能量状态进行模拟，结果显示，孔隙结构对于改变复合结构中的能量分布效果明显，能量穿过孔隙结构后明显衰减。刘海燕等[13]对泡沫混凝土高应变率状态下的吸能特征进行了实验探究，总结了泡沫混凝土在抗冲击过程中的变形规律。叶燕华等[14]在空心砌块墙体中分别注入、不注入泡沫混凝土,并反复加、卸压，对比发现，前者在载荷作用下抗剪强度和极限承载力得到提高，墙体破坏时裂纹扩展分散、速度慢，显示了优良的抗倒塌性能。

岩石类材料以脆性为主，具有较高的强度，但抗变形能力很小。孔隙的引入对岩石类材料特性改变非常大，能提高其隔振能力，但动力学数值模拟中对刚性转角大变形的分析一直比较困难，因为数学上需要进行近似处理。最近提出的四维离散弹簧元法(4D-LSM)通过四维空间的相互作用，一定程度上解决了这个问题[15]，该方法可以较好地处理动态大变形问题。笔者先对4D-LSM用于单个岩石圆环模型的适用性进行了验证；研究了单个岩环模型在不同条件下的破裂形态以及动态变形和能量抵抗能力；对含有随机孔隙结构的岩环阵列模型的动态能量吸收特性和尺寸效应进行了分析。

1 四维离散数值方法4D-LSM

1.1 模型简介

4D-LSM是在三维离散弹簧元法(DLSM)的基础上发展的。在DLSM[16]中，模型由弹簧和离散球形颗粒连接构成，颗粒之间的连接弹簧包括法向和切向两个方向。DLSM使用相同的颗粒模型可以产生不同的晶格结构，从而表征不同的宏观力学行为。与传统离散方法相比，DLSM无需宏观参数校准，自由度是离散单元法(DEM)的一半，且容易进行并行处理。DLSM中切向弹簧根据局部应变进行计算，具有旋转不变性。4D-LSM[15]基于平行世界的概念，在DLSM的基础上引入第四维度构造“四维超薄膜”，通过三维模型与平行世界中的模型建立相互作用关系，有效解决了传统LSM方法中的泊松比限制问题，4D-LSM的原理图见文献[15]。相对于经典连续介质力学，4D-LSM的离散性使其更适合模拟岩石或类岩石等非均质材料的破坏问题。

1.2 理论公式

与DLSM相比，4D-LSM的力和法向矢量具有4个分量。在4D-LSM中，代表三维相互作用的弹簧刚度(k3D)全部相同，而代表四维相互作用的弹簧刚度出现差异，差异特征由四维刚度比λ4D表征。为了获得弹性的各向同性，四维相互作用中弹簧刚度通过式(1)进行调整。

kα=kβ=4/3kγ=λ4Dk3D

(1)

式中：kα、kβ、kγ是特定的第四维刚度。组成模型的颗粒运动状态满足牛顿第二定律

(2)

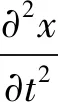
Fij=kunnij

(3)

式中：Fij为从颗粒i到颗粒j的力；nij为从颗粒i到颗粒j的法向量；k为弹簧的刚度，un为弹簧的变形量，其计算式为

(4)

式中：x为颗粒当前位置，x0为颗粒初始位置，|•|为获取矢量的法线。法线方向计算式为

(5)

1.3 参数选取

四维离散弹簧模型被视为虚拟固体，其特征由两个参数表征：弹簧刚度k和四维刚度比λ4D。对于λ4D，有式(6)所列多项式方程。

λ4D=-211.134 937 79v3+162.846 558 51v2-

55.424 497 19v+6.929 022 00

(6)

式中：v为泊松比。弹簧刚度k计算公式为

(7)

式中：V为模型的三维体积；E为弹性模量；li为第i个弹簧的长度；η为泊松刚度比率，其计算式为

1.003 692 23

(8)

2 岩石圆环模型计算验证

2.1 计算模型

建立半径R为50 mm、厚度T为50 mm的圆盘，组成圆盘的球形颗粒直径为1 mm。探究4D-LSM对于研究圆环劈裂的适用性，以10 mm为一个梯度，在圆盘模型中分别挖去半径为10、20、30 mm的同心圆孔，如图1所示。用参数δ来表征内外径之比，即δ=r/R(δ=0、0.2、0.4、0.6)。模型弹性模量、泊松比、密度的设置参考卡拉拉大理石，系统具体输入参数如表1所示。

图1 不同孔径比的圆环模型和破坏模式Fig.1 Rock ring models with different hole- diameter ratios and failure

弹性模量/GPa泊松比密度/(kg·m-3)弹簧抗拉伸长量/μm时间步长/s阻尼490.193 0000.1411×10-70.3

因巴西圆盘劈裂实验中加载端存在应力集中问题，有学者对试样进行改进[17]，将加载端打磨成两个相互平行的平面，使线载荷转化为面载荷，有效地保证了圆盘试样的中间起裂。对于4D-LSM模拟劈裂问题，模型采用速度控制的加载方式，速度作用在模型最上层颗粒面和最底层颗粒面，加载角度φ为16.1°。对所有模型最上层的颗粒面设置大小为4 mm/s的垂直向下速度；最底层颗粒面沿垂直方向速度设为0，表示对模型的底端的固定。

2.2 验证

将δ=0时的圆盘模型考虑成圆环模型的特殊情况。由图1可知，当δ值为0、0.2时，模型表现出单一的纵向拉伸破坏，试样破坏成两部分；δ值等于0.4、0.6时，模型同时表现出纵向和横向拉伸破坏，模型破坏成4部分。这表明，随着δ值的增大，模型破坏裂纹数量表现出增多的趋势。由图1可知，通过4D-LSM模拟岩石圆环模型的加载，得到的破坏形态与前人[18-19]得出的物理实验结果相吻合。

将模型加载峰值载荷除去πRL进行标准化处理，即抗拉强度σt=Pmax/πRL。为对4D-LSM求解的圆环模型的抗拉强度与现有文献中的结果进行对比，将各试样的σt除去δ=0时的σt，进行归一化处理。图2为归一化处理后的实验数据[18]、FEM/DEM模拟数据[20]以及4D-LSM模拟数据和拟合曲线，由图2可知数据相差不大。4D-LSM数据拟合曲线的公式为

σt=1.022 7e-3.924 0δ，R2=0.998 2

(9)

岩环模型随着孔径比δ的增加抗拉强度呈指数下降的趋势，δ对模型抗拉强度的影响随着δ的增加逐渐减弱。拟合曲线有效验证了尤明庆等[21]指出的岩环劈裂载荷随内径增加而呈现出指数下降的结论。通过破坏形态、模拟数据两方面证实了4D-LSM对于研究岩石圆环力学特性的可行性。

图2 抗拉强度与孔径比拟合曲线图 (实验和FEM/DEM模拟数据来源于文献[18，20])Fig.2 Fitting curve of tensile strength and hole-diameter ratio(Experimental and FEM/DEM simulation

3 岩石圆环的耗能规律

3.1 厚度与外直径之比

将模型厚度T与外直径D的比值定义为w，即w=T/D，选取δ=0.6的模型，通过设置不同厚度值，探究w(w=0.25、0.50、0.75、1.00)对模拟结果的影响，如图3所示。对孔隙率n、均质度m、颗粒间弹簧抗拉伸长量u3个因素以δ=0.6、w=0.50的圆环模型为基础进行研究。

圆环破坏的载荷-加载点位移曲线中,峰值载荷对应的位移值为模型的动态变形抵抗能力；在动态载荷的作用下，破坏后吸收的能量为模型的动态能量抵抗能力，数值等于载荷-加载点位移曲线中开始加载到峰值载荷的曲线段与横坐标轴围成图形的面积。因该曲线段接近直线，图形近似看成三角形，则模型的动态能量抵抗能力计算式为

Q=Pmax×z/2

(10)

式中：Q为动态能量抵抗能力；z为动态变形抵抗能力。

图3 不同厚径比的计算模型和破坏模式Fig.3 Computational models with different thickness- diameter ratios and failure

由图4(a)可知，不同w值模型的峰值载荷差异较大，但整理数据后发现，圆环模型抗拉强度并未因为模型厚度不同而出现太大变化，均值为0.230 0 MPa。这表明厚度的增加对于抗拉强度不会带来较大的影响。模型的峰值载荷与模型厚度在一定范围内成正比例关系，可以通过调节厚度的大小对模型峰值载荷进行调整。随着w值的改变，动态变形抵抗能力在均值13.360 0 μm上下波动，而能量抵抗能力与w值呈正比例关系，函数表达式分别为

z=13.360 0

(11)

Q=24.251 0w，R2=0.999 9

(12)

图4 不同厚径比计算模型的数值计算结果Fig.4 Numerical simulation results of computational models with different thickness-diameter

3.2 孔隙率

岩石中各类孔洞、裂隙的总体积与岩石总体积的比值称为岩石的孔隙率[22]。分别生成孔隙率为0.05、0.10、0.15、0.20的模型，研究孔隙率对圆环劈裂的影响，如图5所示。从图6(b)中可知，随着孔隙率的增加，抗拉强度呈二次函数下降，拟合曲线为

σt=1.574 1n2-0.869 5n+0.238 5，

R2=0.999 8

(13)

对圆环模型的动态变形抵抗能力和动态能量抵抗能力与孔隙率的关系进行拟合，如图6(c)、(d)所示，圆环模型抵抗变形的能力与动态能量抵抗能力随着孔隙率的增加分别呈幂函数和对数关系下降，表达式分别为

z=9.211 4n-0.086 0，R2=0.997 4

(14)

Q=-2.908 0lnn+0.622 9，R2=0.999 9

(15)

图5 不同孔隙率的计算模型和破坏模式Fig.5 Computational models with different porosities

图6 不同孔隙率计算模型的数值计算结果Fig.6 Numerical simulation results of computational

3.3 非均质性

由于岩石矿物组成成分、粒径以及分布方式的不同，再加上裂隙、节理、孔隙等结构的存在，导致自然界中岩石具有非均质的特性。在4D-LSM系统中，模型材料的均质性符合韦布尔分布函数，用参数m表征材料的均质度，m值越大均质度越高。对圆环模型m值分别设置为5、10、20、30进行圆环劈裂实验，如图7所示。载荷-加载点位移曲线如图8(a)所示，峰值载荷随均质度的增加逐渐增大。抗拉强度与均质度的拟合式为

σt=0.024 1lnm+0.135 5，R2=0.976 9

(16)

模型的动态变形抵抗能力和动态能量抵抗能力随着m值的增加分别呈对数关系增加，表达式分别为

z=1.561 7lnm+7.205 0，R2=0.981 4

(17)

Q=2.244 4 lnm+2.998 9，R2=0.980 0

(18)

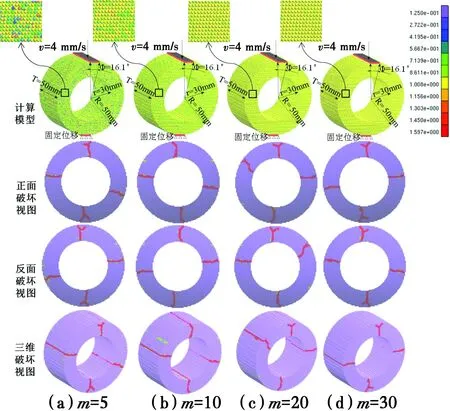
图7 不同均质度的计算模型和破坏模式Fig.7 Computational models with different homogeneity

图8 不同均质度计算模型的数值计算结果Fig.8 Numerical simulation results of computational models with different homogeneity

3.4 脆性小变形破坏

将圆环模型颗粒间弹簧抗拉伸长量u分别设为0.10、0.15、0.20、0.30 μm，进一步探究脆性阶段圆环破坏与u的关系。圆环模型载荷-加载点位移曲线如图9(a)所示，4条曲线表现出了极高的相似性，说明颗粒间弹簧抗拉伸长量的改变对载荷-加载点位移曲线的走势影响不大。抗拉强度与颗粒间弹簧抗拉伸长量的拟合线如图9(b)所示，直线方程为

σt=16.555 0u，R2=0.998 9

(19)

模型的动态变形抵抗能力和动态能量抵抗能力随着u值的增加分别呈正比例函数和二次函数关系增加，表达式分别为

z=95.046 0u，R2=1.000 0

(20)

Q=571.800 0u2+16.453 0u-1.214 8，

R2=0.999 9

(21)

图9 不同弹簧抗拉伸长量的计算模型数 值计算结果(小变形阶段)Fig.9 Numerical simulation results of computational models with different spring tensile elongations (the stage of small deformation)

3.5 大变形破坏

将u分别设为0.04、0.08、0.12、0.16 mm，对圆环模型大变形阶段的破坏模式和耗能特征进行研究，如图10所示。结果表明，大变形阶段圆环模型抗拉强度拟合曲线区别于小变形阶段的正比例函数，更接近二次函数，函数关系式为

σt=-2 050.900 0u2+1 776.800 0u-4.222 2，

R2=0.999 8

(22)

大变形阶段圆环模型动态变形抵抗能力与小变形阶段正比例函数相比也转化为幂函数关系，拟合公式为

z=114.430 0u1.048 0，R2=0.999 9

(23)

与小变形阶段相比大变形阶段圆环模型的动态能量抵抗能力表现出了相同的二次函数规律，函数表达式为

Q=481.670 0u2+20.356 0u-0.648 5，

R2=0.999 6

(24)

图11为大变形阶段(u=0.16 mm)圆环模型破坏过程图。通过对u的设置提高模型变形量，以对圆环的大变形破坏过程进行模拟，研究发现，与脆性小变形阶段相比，不仅圆环模型动态变形抵抗能力和动态能量抵抗能力增加，圆环模型的破坏模式也发生根本转变：从小变形阶段破坏成4部分，演变成仅纵向发生拉伸破坏。

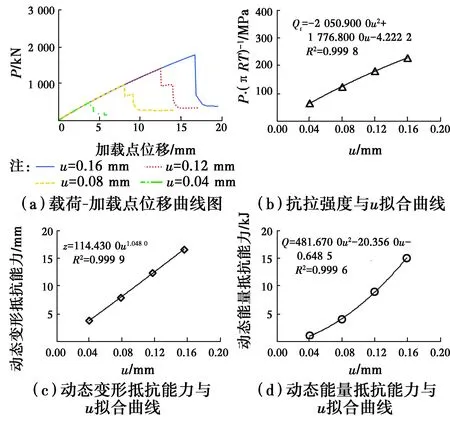
图10 不同弹簧抗拉伸长量的计算模型数值 计算结果(大变形阶段)Fig.10 Numerical simulation results of computational models with different spring tensile elongations (the stage of large deformation)

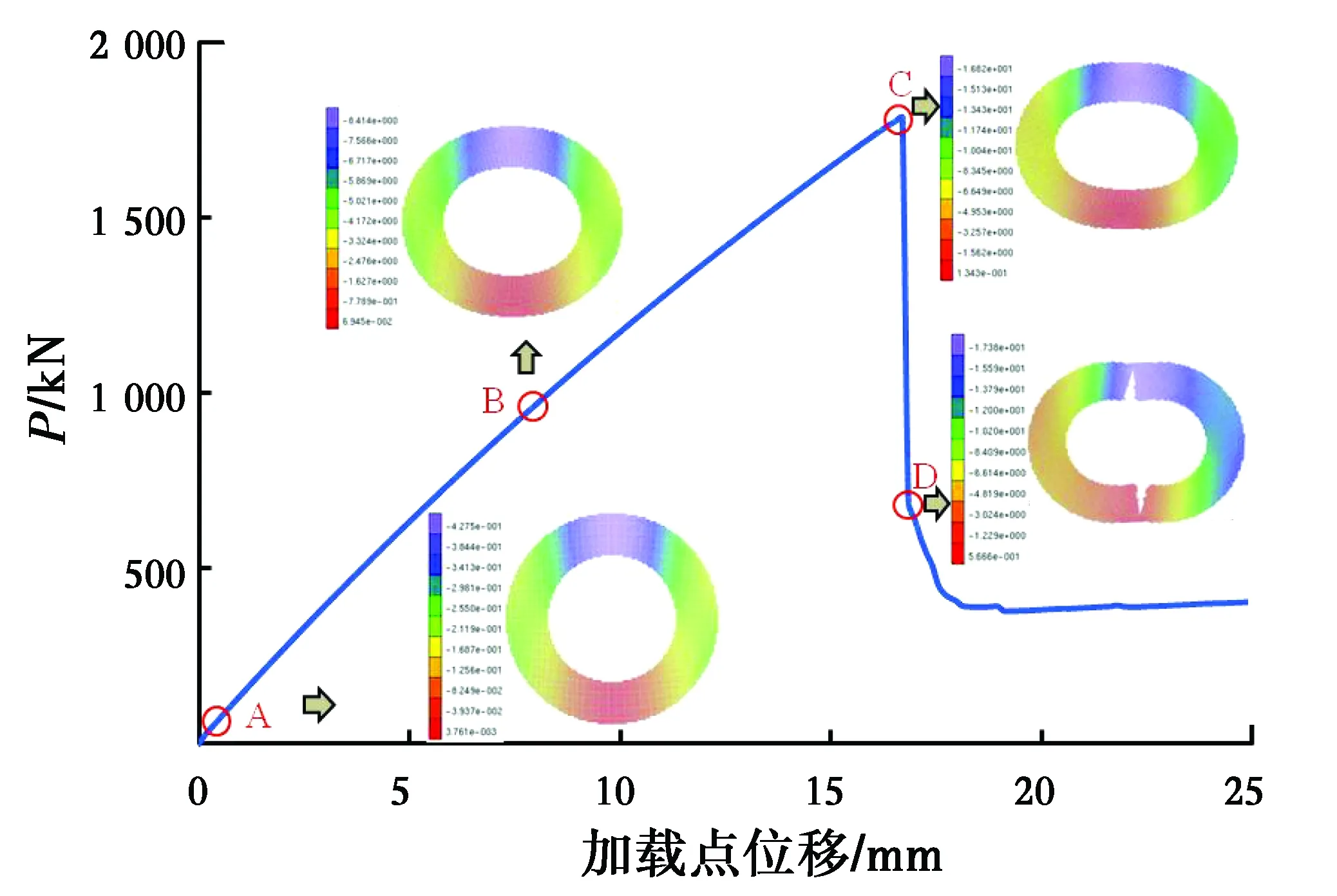
图11 大变形破坏过程图Fig.11 The failure process of model in large

3.6 岩环组合体

以δ=0.6、w=0.5、n=0.15的圆环模型为单元，分别建立N×N(N=1、2、3、4)的圆环阵列模型，如图12所示，通过N对组合体模型尺度进行表征。对模型抗变形能力进行研究，对比不同组合体模型的载荷-加载点位移曲线发现，随着N的增加，圆环阵列模型的峰值载荷也逐渐变大，但第2峰值载荷与第1峰值载荷相比逐渐弱化。圆环阵列模型的第1峰值载荷Pmax与N呈正比例函数关系，表达式为

Pmax=1.135 6N，R2=0.999 9

(25)

对岩环组合体模型的动态变形抵抗能力和动态能量抵抗能力进行分析，如图13(c)、(d)所示，发现岩环组合体的变形抵抗能力随着N的增加呈正比例增加，而动态变形抵抗能力与N呈幂函数关系。函数表达式分别为

z=10.748 0N，R2=0.999 8

(26)

Q=6.176 9N1.990 2，R2=1.000 0

(27)

对组成阵列材料圆环单元的动态变形抵抗能力和动态能量抵抗能力进行分析，如图13(e)、(f)所示。圆环单元的动态变形抵抗能力和动态能量抵抗能力随着N的变化基本没有改变。单位圆环的变形抵抗能力均值为10.799 0 μm，能量抵抗能力均值为6.129 3×10-3J,可知圆环单元在能量吸收方面几乎不受阵列模型尺度的影响。

图12 不同尺度的岩环组合体计算模型和破坏模式Fig.12 Rock ring combined computational models with different scales failure

图13 不同尺度岩环组合体计算模型的数值计算结果Fig.13 Numerical simulation results of rock ring combined computational models with different

4 讨论

根据不同因素下岩石圆环模型的破裂形态可知，孔隙率、非均质度均能引起圆环模型裂纹扩展形态的改变，但总体来说竖向裂纹差异较小，横向裂纹大体在圆环腰部水平线附近上下浮动；厚径比对裂纹扩展有一定影响，主要表现为横向次生裂纹的数量差异。通过对孔隙度或均质度设置合理的参数，圆环模型破坏形态表现出了较规则的“四扇叶形”，如图5、图7所示，与前人实验中所得破坏形式吻合[18-19，23]。由此可见，通过对圆环模型的均质度或孔隙率设置合理的参数，4D-LSM可以对岩石圆环模型的破坏模式进行良好的再现。

圆环模型厚度的增加并不会带来抗拉强度和变形抵抗能力的增加，但能量抵抗能力随着w值呈正比例增长。孔隙率的增加会导致圆环模型抗拉强度、变形抵抗能力与能量抵抗能力的不同规律下降，但总体而言，对变形抵抗能力影响幅值较小，抗拉强度、能量抵抗能力降低幅值较大。抗拉强度、变形抵抗能力、能量抵抗能力随着模型均质度的增加而出现不同规律增大，由此可知，非均质性是影响岩石强度的一个重要因素，通过均质度的提高可以有效改善圆环模型的隔振性能。与小变形阶段抗拉强度与变形抵抗能力的线性增长相比，大变形阶段得到了非线性的规律和不同于现有实验和数值的破坏结果。由此可知，当对类岩石材料(如混凝土等)通过加强材料韧性如添加纳米材料进行改性时，其对应圆环模型的耗能与抗变形能力将会有大的提升，破坏模式与脆性阶段相比也将表现出较大差异。

岩环组合体模型破坏形式主要表现为45°斜向破坏带贯穿模型，导致模型丧失承载能力。组合体模型虽然总体上承受压力，但本质上仍表现出圆环单元的受拉破坏，圆环单元破坏成4部分。不同尺度组合体模型中，各圆环单元表现出不同的破坏形态，但圆环单元的变形特征和耗能规律却与单个圆环受载荷作用时表现一致。由此可见，对岩环组合体的耗能规律可以通过单个圆环进行较好的表征。基于以上特点，当通过增加孔隙对隔振超材料进行设计时，可先对单个圆环着手研究。

5 结论

1)4D-LSM用于分析岩石圆环破坏的适用性得到验证。模拟结果表明，圆环试样的的破坏形态由多个因素相互耦合共同作用而成。非均质性、孔隙率对圆环模型的破坏形式有着重要影响。

2)分别拟合得出了抗拉强度、动态变形抵抗能力、动态能量抵抗能力与厚径比、孔隙率、非均质度、颗粒间弹簧抗拉伸长量的函数关系式。总结了圆环模型不同因素的抗变形特征和耗能规律。

3)N×N岩石圆环阵列模型的承载强度与N呈正比例关系，组合体模型中圆环单元的动态变形抵抗能力与动态能量抵抗能力不受阵列模型尺度的影响。