结合美国国际数学建模竞赛提升文科生学术能力的研究与实践

陈德强

【摘要】针对文科高等院校学生数学课程教学的实际情况，积极探索将数学建模与教学改革相结合的教学模式，通过改进教学方法和教学模式，不断提高文科生数学建模的应用能力与学术创新能力，试点并实践了文科大学本科生参与美国国际数学建模竞赛的组织、教学、培训、参赛等整个流程并取得了阶段性的成果.

【关键词】美国国际数学建模竞赛;文科院校;教学方法改革

【基金项目】2017年度华东政法大学校级教改项目（A-0316-17-00304），文伯书院《高等数学》通识课项目（A-0312-18-174796）.

一、文科院校大学数学课程的现状及改革的必要性

一直以来，虽然笔者所在学校作为一个以文科为主的大学，但依然有大量的数学文化基础课程，这些课程的考核如果仅以试卷上的数学试题作为评价学生的主要依据是片面的，这不利于培养本科生对数学的实际应用以及学术能力还远远不够.这些课程包括各学院开展的“高等数学”“线性代数”“离散数学”“概率统计”“数理逻辑”等课程，很多学生仅仅为了考个高分，通过大量刷题的方式应付数学考试，却无法将所学的数学知识真正融会贯通，应用于具体的学术研究中.

针对这个问题，美国的韦恩州立大学表示，大学就是要培养大学生在实践中的定量推理能力和批判性思维能力.不仅仅是培养理工科学生具有这种能力，更要让艺术、人文、法学和社会科学领域专业的学生在数学学习上获得同等能力.他们通过鼓励学生参与对数学模型和数学问题的定量和定性分析提高相关能力.美国的密歇根州立大学也积极鼓励学生用公式、图形、表格和图表的形式解释数学模型：比如，能够通过不同的方式（如视觉的、文字的、数字的等）呈现数学信息;可以通过运用概率、代数、几何和统计方法去解决问题;能够借助定量数据分析，清晰地表达自己对一个社会科学问题的观点和认知等.在相关的课程中，鼓励大学生探索具体环境下的人口爆炸式增长统计（包括婴儿出生率、家庭收入、教育程度等）、病毒的传播、医学检验中的贝叶斯模型、经济中的博弈等.这让数学不再只是课上简单的“公式”，而是成为可以在现实世界中真真正正应用的优秀工具.

为了建设中国的双一流高校和专业，国内的文科院校也不能驻足不前，一直停留在老套的教学大纲里，美国国际大学生数学建模竞赛就是一个很好的契机，它给我们更新文科的数学课程的教学大纲提供了一个很好的范例[1].因此，应该加快推进文科院校数学课程的改革，结合国际数学建模竞赛，使得学生在充分学习课程的基础上，参与国际大赛，设计数学模型，应用算法和编程解决实际问题，撰写学术论文，这个机遇为教学改革提供了一条崭新的途径.

二、文科院校大学数学课程提升学生学术能力的措施和方法

大学生运用数学建模解决实际问题的能力提升，不是一朝一夕的事情.这需要把数学建模的意识始终贯穿于数学教学过程之中，也就是要不断地引导大学生用数学思维的观点和眼光去观察、分析和解释各种对象之间的关系，从复杂纷繁的具体问题出发，逐步抽象出一些课程中介绍的数学模型，进而逐步达到利用数学模型来解决实际的数学问题，使得数学模型的观念成为文科大学生定量思考问题的第一方法和习惯[2].

（一）以数学基础课程为平台，在教学过程中增强学生的数学建模意识

在“高等数学”的教学中，有很多可以和数学建模相结合的知识点展开[3]，在讲课的过程中，注意延展学生的思维和拓展举例的广泛性.不要拘泥于教材上的几个例题，可以以课外阅读或者书写读书笔记的形式培养学生数学建模意识.例如，高数课上有一章专门学习微分方程的求解，但是课内所学的一阶线性微分方程，伯努利方程可以求解的范围都十分有限.在课堂拓展中首先介绍如何将一个连续的函数离散化，以便于取点分析.常见的利用Taylor多项式近似离散的方法不但可以得出数值解还便于进行误差分析.进一步可以介绍欧拉方法求解微分方程并利用泰勒展開式进行2阶精度的误差分析，为提高精度，继续研究欧拉方法的改进，通过积分的梯形公式进一步缩小误差，最终得出改进二阶法.就这样一步步引导学生的思路，逐步深入，并演示如何用MATLAB软件求解微分方程.

（二）分小组进行讨论，在解决数学建模问题过程中增强学生的学术写作水平

文科院校的数学课程的许多知识点和建模大赛等结合紧密，因此，需要选好教学内容，提高学生学习和参与竞赛的积极性.我们根据教学情况，选取一些实际问题让学生讨论，既能结合学生自身的文科专业背景提高学生的问题分析能力，又能反映最新的科学技术思想.通过采用启发式和讨论式相结合的教学方法，通过提出一些实际问题，让学生充分思考、展开讨论，甚至让他们上讲台展示自己的处理方法、见解，既活跃了课堂气氛，又达到了引导学生学习运用工具分析、解决实际问题的目的.在课程讲授过程中，除了正常的作业外，还适当给出一些实际问题让学生自己建立数学模型，并根据建立模型的基本步骤，要求完成包括建模假设、建模过程、模型求解、模型优缺点及局限性的讨论等，最后形成小论文[4].例如，“概率统计”课程有一些内容涉及预测模型，我们引导介绍马尔可夫链通常用来解决排队理论和统计学中的问题.我们试图让学生根据这个模型进行创新性思维，解决一个实际问题：

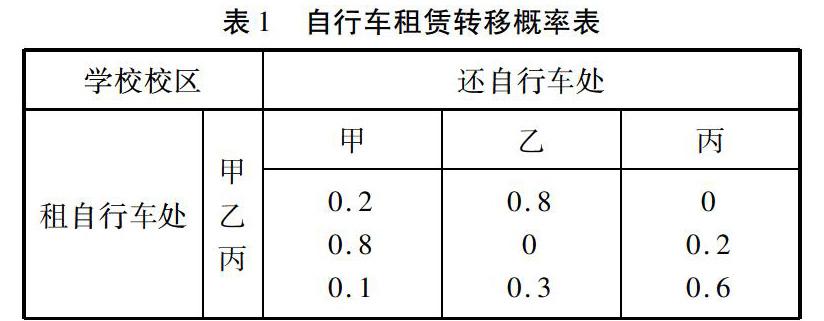
为适应日益扩大的社会共享经济发展的需要，大学城的甲、乙、丙三个高校校区成立了一个自行车租赁联合项目，联合租赁大学生骑行自行车的业务.大学生可由甲、乙、丙三处任何一处租出自行车，用完后在三处中任意一处进行归还即可.估计其转移概率如表1所示.今欲选择其中之一开设自行车维修点，问该维修点设在哪一个学校校区最好？

经过引导学生计算马尔可夫链模型，得出结论.由于还到甲校区的自行车较多，因此，维修点设在甲校区较好.但由于还到乙校区的自行车与还到甲校区的相差不多，若是乙校区的其他因素更为便利，如交通比甲校区更方便，便于自行车零配件的运输，电力供应稳定便于充气等等，亦可考虑设在乙校区.

这就激发了学生学习知识的动力，并且用于解决实际问题，为以后进行毕业设计或者学术论文研究打下坚实的数学模型基础.

（三）积极开展大学数学实验第二课堂，将数学建模与实验有机结合

在实验实践中，我们就在创新实验室安装相应环境，引导学生通过实验，开展模型计算和优化活动.

例如，在介绍电脑鼠走迷宫搜索算法模型的时候，一位文科的本科学生在查阅走迷宫算法的基本资料后写下读后感：“阅读完本算法，我发现想要分析这个算法不是很容易.小小的电脑鼠走迷宫需要那么多算法的步骤，首先从电脑鼠方向确立、迷宫坐标以及墙壁的建立，随后再进行迷宫路径的搜索.在搜索完毕之后，再对迷宫的地图做一次最优路径的选择并且制作等高图，最后对电脑鼠整个进行软件构架.而整个算法中最难、最复杂的是等高图的制作算法，这张图是电脑鼠最快走完迷宫的保障，若是等高图的制作算法有微小的差异，那将会给电脑鼠搜索迷宫最优路径的选择造成很大的影响，可谓相当艰难.在了解了本算法之后，深深感觉自己的算法功底还是很薄弱的，在以后的学习中，加强对算法的研究，毕竟算法是所有程序的基础.程序没有了算法，就没有了灵魂”.

三、文科院校建模实践小组如何组织、筛选、培训活动及参加比赛

第一阶段：人员筛选，图书和实验室配备.

初选队员：来自历届参赛老队员、高数竞赛获奖学生、任课教师推荐的优秀学生，考虑到中途会有参加培训队员中途退出或加入，为保证最终参赛队员质量，初选队员规模控制在20人左右.通过QQ群召集初选的队员，对数学建模竞赛培训进行动员，并由参加历年数学建模竞赛获奖的同学为大家介绍经验.在确定总的参加人员后，将参赛学生分组，三人一组，根据以往经验，每组最好一名负责计算机算法的学生，一人负责翻译和论文排版，另外一人负责数据收集和模型分析，三人选出一个组长.由于培训的人数较多，纪律方面必须严格，管理需有序安排，为此制订了相关的实验室守则，并配置好实验环境.

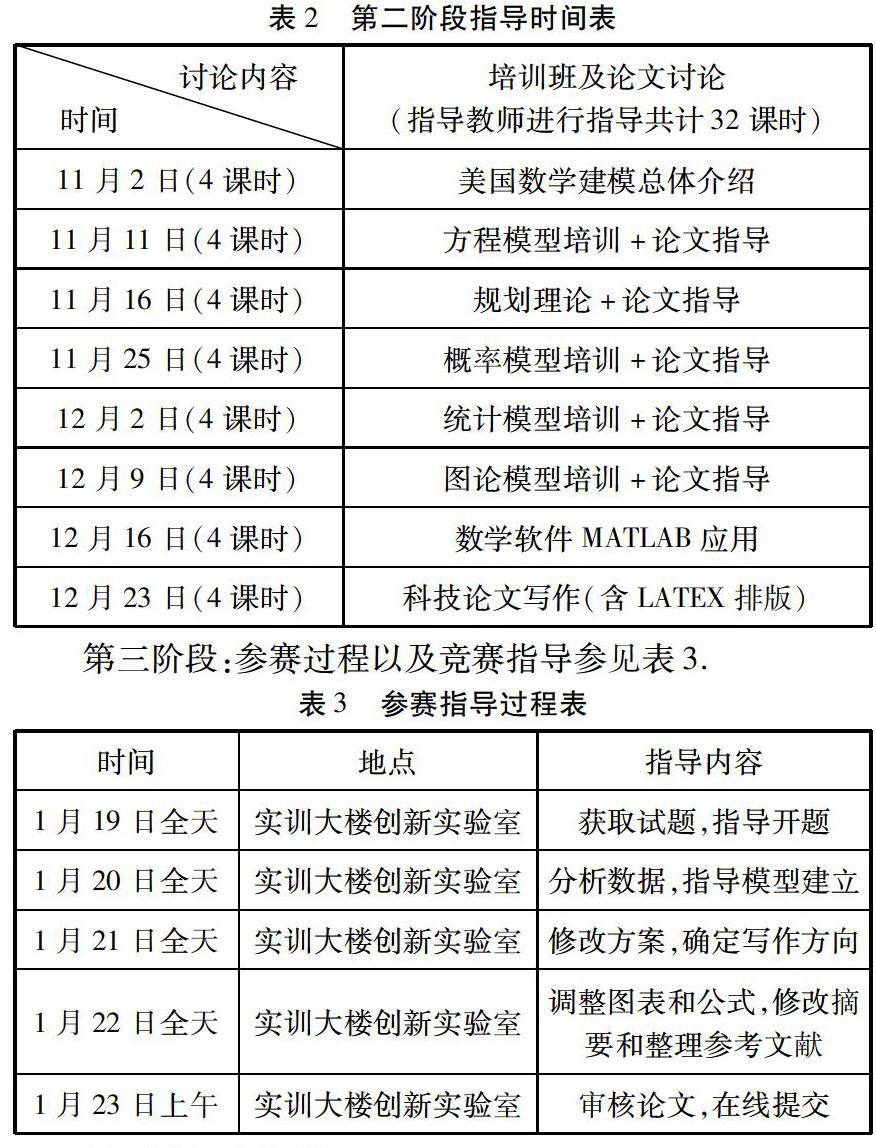
第二阶段：中期培训指导和优秀论文讨论[5].每周讲座时间要保证4个学时，然后分组讨论一对一指导参见表2.

四、总结以及展望

经过全组教师同学的不懈努力，历时96小时.笔者所在学校6支代表队伍、共18名学生参加比赛.笔者所在学校本科生在去年获奖的基础上，今年再次获得1个二等奖，5个三等奖.其中获得二等奖的同学挑战了难度较大的E题，建立了一个城市可持续发展和智能评价指标体系模型，并进行了模拟仿真评估，给出了城市未来几十年内的可行性增长计划.通过比赛，提升了文科大学本科生运用所学数学知识，结合自己的文科背景特长，解决学科交叉领域前沿实际问题的能力，激励与提高了学生应用所学的数学模型和计算机算法解决实际问题的科研能力，促进了本科生学术水平和创新能力的提高.我们将不断总结经验，为培养更多的高层次的文理兼备的复合型人才而努力.

【参考文献】

[1]王茂芝，郭科，徐文皙，等.数学建模中的创新意识培养[J].大学数学，2009（1）：126-129.

[2]樂励华，戴立辉，刘龙章.数学建模教学模式的研究与实践[J].工科数学，2002（6）：9-12.

[3]张勇，黄廷祝，傅英定.数学建模思想融入微积分课程教学初探[J].大学数学，2010（2）：158-160.

[4]姜启源.数学实验与数学建模[J].数学的实践与认识，2001（5）：613-617.

[5]王茂芝，徐文皙，郭科.数学建模培训课程体系设计探讨[J].数学教育学报，2005（1）：79-81.