基于流固耦合理论的关机水击特性

张凯宏，江 欣，肖明杰，梁树强 ，胡 伟，冀 鹏

(1.西安航天动力研究所，液体火箭发动机重点实验室，陕西 西安 710100;2.航天推进技术研究院，陕西 西安 710100)

0 引言

随着航天技术的发展，航天器对其推进系统的技术指标要求也越来越高。特别是对于起轨道机动功能的轨控动力系统，其推力越来越大、室压越来越高、响应时间越来越短[1-3]，导致管路系统流量大、压力高，关机时形成的管路水击压力急剧增加，严重时引起管路的泄漏和破坏。因此，了解管路系统水击特性，采取措施减小水击峰值压力成为轨控发动机管路系统设计中需解决的突出问题。

水击[4-6]也称液压冲击或“水锤”现象，是由于液体局部加速度过大所致的管内压强急剧变化的一种动态现象，这种现象经常出现在液体火箭发动机的起动、关机以及转工况过程中。尤其在关机过程中出现的水击峰值压力可以达到管路正常工作压力的几倍甚至几十倍，这种突然的压力大幅升高会导致管路系统破裂、推进剂泄漏，进而导致推进系统工作异常。水击的数值计算方法主要包括特征线法和有限体积法等。特征线法[7-8]理论比较完善，且不受管道系统复杂程度的限制，但不利于解决多特征插值与非积分项误差的问题。有限体积法[9-10]能较好地反映水击压强，同时克服了特征线法计算的水击压强波动幅度较大、衰减较慢的问题。

水击波在沿管道运动的过程中，会诱发管路结构振动，这一振动又影响压力的波动过程和流体的流动过程，形成以流体的瞬时流动、流体波动以及结构振动为一体的振动系统。3种运动形式间的相互作用称为流固耦合[11-13]。流固耦合效应会影响水击的峰值压力和衰减速率，基于流固耦合对水击特性进行分析能得到更准确的结果。对于水击压力比较高的环境，忽略结构变形对水击的影响，将会对水击仿真带来较大误差。近年来，国内外学者开始利用流固耦合对水击等问题进行仿真。2014，Cesana等[14]对两根同轴管路的水锤响应进行了流固耦合分析，并验证了基于流固耦合模拟水击压强的准确性。2015年，朱雨[15]将入口设置为脉冲流体速度入口边界条件，研究了管路水击压力脉动诱导结构振动的流固耦合相互作用机理和结构动力学响应规律。

为了验证考虑流固耦合的水击仿真适用性，本文基于Workbench协同仿真环境[16-17]，分别在Fluent仿真软件和Transient Structural软件内设置流体和固体相对应的作用面，并在System Coupling内实现数据的相互传递。

1 物理模型和计算方法

1.1 流体控制方程

阀门关闭过程是一个动态过程，管道中流体为非稳态湍流流动，控制方程如下：

1)连续方程

(1)

2)动量方程

根据运动守恒定律，管路流体的运动方程的基本形式可写成：

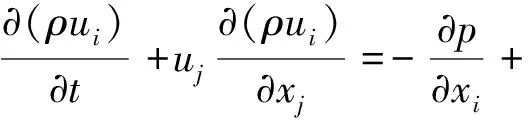
(2)

3)湍流模型

采用标准k-ε湍流模型来使上述方程封闭。

k方程：

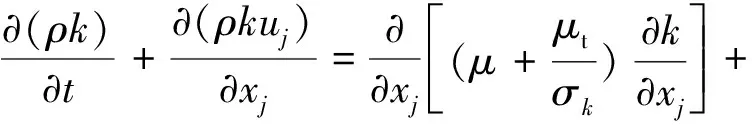
(3)

ε方程：

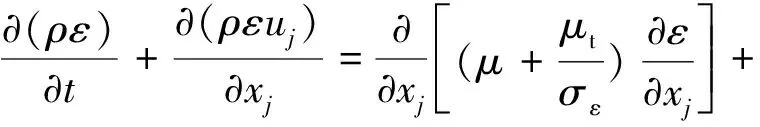
(4)

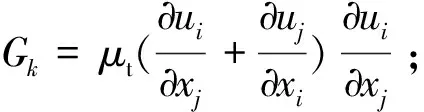
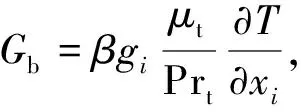
1.2 固体控制方程

管路结构动力学控制方程如下：

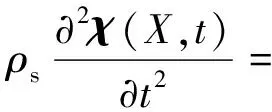
(5)

σ=FST

(6)

(7)

S=λsTr(E)I+2μsE

(8)

式中:σ为应力张量；F为变形梯度；S为二阶Piola应力；E为格林-拉格朗日应变；I为单位矩阵；λs和μs为Lame常数；ρs为管路材料的密度，kg/m3；fs为体积力。

1.3 流固耦合方程

流固耦合遵循力和位移的守恒原则，所以在流固耦合交界面处，应该保证流体与固体结构的应力、位移等基本参数数值相等。即满足如下2个方程：

(9)

式中：下标f为流体；s为固体。

2 算例验证

2.1 算例验证模型

本文基于文献[18]中的管路在阀门关闭时所产生的水击过程进行基于流固耦合的数值研究。试验管道内径10 cm，壁δ=7 mm，长度L=24.47 m,沿程损失系数由试验测得λ=0.033 1，文献中没有说明阀门的具体形式，在此选择比较常见的球阀。如图1所示取球阀阀芯及前后直管段中全部流体为计算区域。靠近管壁处的网格用边界层网格加密，如图2所示。

图1 模型及球阀结构Fig.1 Model and structure of ball valve

图2 管横截面网格Fig.2 Mesh of profile of pipe

2.2 仿真环境及设置

为了实现数值模拟管路水击双向流固耦合作用过程，本文在研究中利用 Workbench15.0 平台，通过联立 Fluent + Transient Structural + System Coupling三部分分析模块构建双向流固耦合分析系统。流固耦合仿真平台如图3所示。

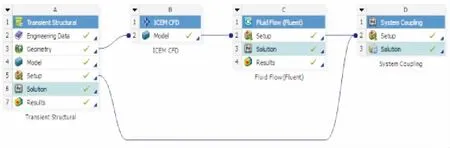
图3 流固耦合仿真平台Fig.3 The simulation platform of FSI

阀门的开关过程采用Fluent中的滑移网格技术实现，将球阀与左右管路流体部分的接触面定义为interface交界面。在阀芯的转动过程中，两个交界面互相接触的部分为interior内部面，流体可以通过该面进行流动，不接触的部分设置为不可流通的固体壁面(wall)，没有流体通过。当两个交界面完全脱离时，全部交界面成为壁面，以此来模拟阀门完全关闭时的状态。阀门的转动规律使用UDF控制，阀门从0.2 s开始作动，以1.75 rad/s的角速度绕中心轴匀速旋转0.77 s，从而实现阀门关闭过程。

根据试验数据，管道进口截面压力保持恒定，定义为压力入口，总压16.4 kPa。出口截面定义为压力出口，静压0 Pa。管壁粗糙度设置为0.000 6，流体为可压缩液体水，设置管壁为动网格，动网格类型为system coupling。

结构计算中，设置管内壁为流固耦合面。system coupling设置中，设置流体与固体的耦合面实现力与位移的数据传递。

2.3 计算结果分析

水击过程的试验与仿真的压强变化如图4所示，为了评估仿真结果与试验结果的吻合程度，利用峰值压力、衰减速率、水击频率的误差来进行评估。

峰值压力误差：

(10)

衰减速率误差：

(11)

水击频率误差：

(12)

式中：下标1为试验值；下标2为仿真值；pm为峰值压力，定义为水击最大压力与水击前初始压力之差；t为衰减时间，由于稳态压力相对于峰值压力较小，认为当压力在稳态压力的±20%之间达到稳态，衰减时间为阀门开始作动到达到稳态所用的时间；f为水击频率，用峰值压力到第二个波谷的时间(1.5个周期)来计算水击频率。

从图4中可以看出，基于流固耦合的水击仿真可以较好的模拟水击压力第一次上升和下降的过程，与试验曲线吻合度较高。表1为仿真结果与试验的误差值。从表1中看出，仿真值与试验值的峰值压力误差和衰减速率误差分别为7.47%，5.56%。基于流固耦合的水击仿真可以较好地模拟水击的峰值压力和衰减过程。仿真值与试验值的水击频率误差为27.47%，虽然误差超过20%，但依然可以看出水击过程中的振荡趋势。因此，基于流固耦合的水击仿真，可以得出较为一致的水击特性。

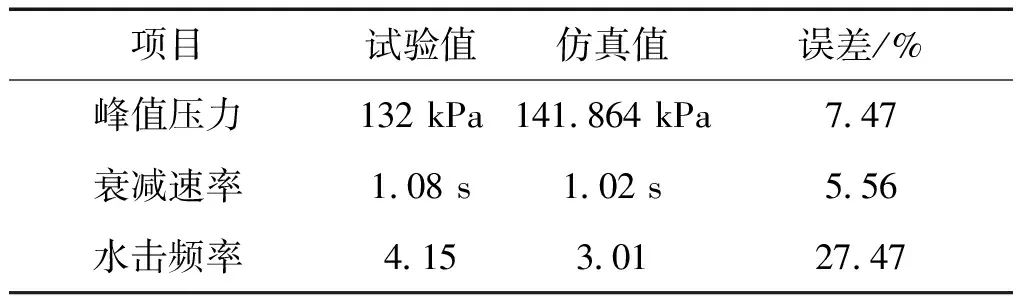
表1 仿真值与试验值误差

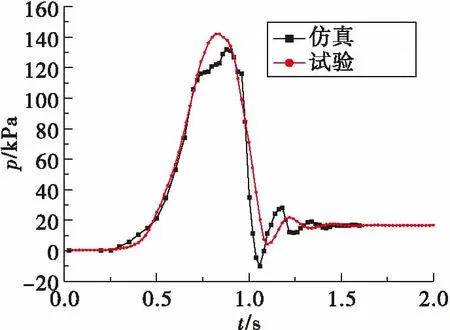
图4 仿真与试验水击压强变化曲线Fig.4 Water hammer pressure of simulation and experiment

3 水击特性

3.1 模型及边界条件设置

根据轨控发动机管路短、半径小的结构特点与压力高、流量大、响应时间短工作特点，对研究管路的尺寸和工作条件作如下更改：减小管路直径、壁厚和管路长度，直径为0.028 m，壁厚为0.001 m，管路长度为0.5 m；增加出口背压和流量，背压设置为1 MPa，4 MPa，6 MPa，流量设置为7.1±0.1 kg/s，7.55±0.1 kg/s，8.0±0.1 kg/s，8.45±0.1 kg/s；缩短阀门关闭时间，阀门关闭时间为0.02 s，0.04 s，0.06 s。研究共设置8个工况，具体设置如表2所示。

仿真环境设置分为结构组件设置、流体组件设置、耦合组件设置，时间步长均为0.001 s，结束时间0.2 s。结构组件设置：选择workbench中Transient Structural计算结构，设置管路内壁面为流固耦合面。流体组件设置：选择workbench中Fluid Flow(Fluent)计算流体，type选择Pressure-Based，time选择Transient，model选择Standardk-ε湍流模型，Materials设置为water-liquid (compressible-liquid)，阀门关闭使用udf控制阀芯运动，阀芯从0.05 s开始作动；进口为pressure-inlet，总压根据流量要求设置，出口为pressure-outlet，静压根据要求设置，温度均设置为298 K；使用interface实现不同域之间数据的连通，将管壁设置为system-coupling动网格；Solution Method设置为Coupled Second Order；时间步长0.001 s，计算时间步数200，每时间步计算200步。耦合组件设置：将结构域的内壁和流体域的管壁创建数据传递，实现位移与压力的数据传递。

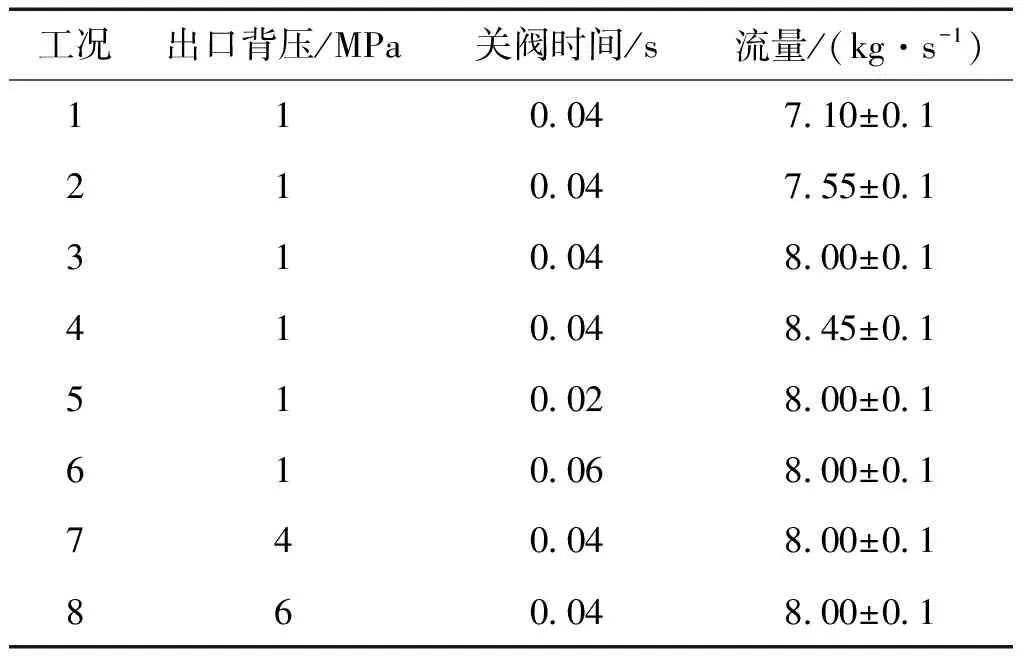
表2 不同工况工作条件

3.2 水击特性分析

图5为工况1不同时刻压力和流线分布图。0.05 s时，阀芯开始转动，此时压力分布均匀，流动趋于稳定。0.06 s时，阀芯转动25%，此时阀门处压力升高，压力波向入口处传播。0.07 s时，阀芯转动50%，压力急剧上升，阀芯前管路出现涡，但涡流较小，压力波已经传播到入口处，入口处压力升高。0.08 s时，阀门转动75%，阀芯前管路涡增大，压力波继续向入口处传递，压力继续升高，此时贴近壁面处未出现逆流。0.085 s时，阀芯转动87.5%，压力波开始向阀门处传递，压力开始降低，阀芯前管路涡增大，在管路中间区域，在壁面位置存在逆流，在壁面位置首次出现细长涡流。0.09 s时，阀门完全关闭，压力波继续向阀门处传递，压力继续降低，壁面位置涡继续增加。通过压力分布的变化可以看出压力波的传播过程，先从阀芯处传递至入口处，此时压力升高；之后压力波从入口处传递至阀芯处，此时压力降低。从图中可以看出，在水击发生过程中，管路中心位置为正向流动，贴近壁面的流动为逆向流动，因此形成涡流。

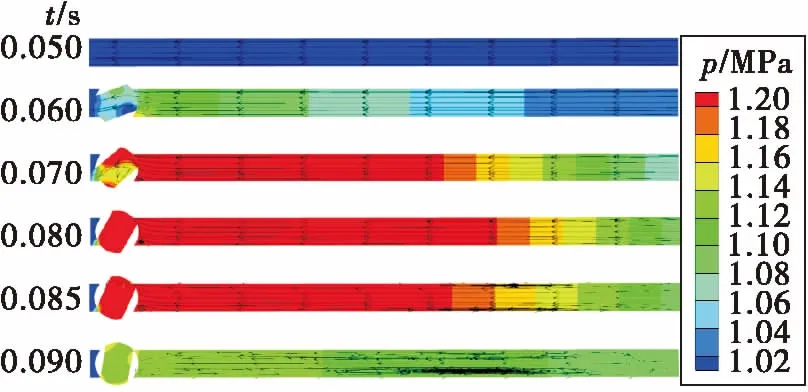
图5 不同时刻压力和流线分布图Fig.5 Pressure and streamline at different time

图6为0.05 s时入口压力分布图，此时流动速度较高。图7为阀门关闭后入口压力分布图。0.085 s时，中心处速度约为0.2 m/s，边界层为逆流，与流线分布图吻合。0.09 s时，入口处全部为逆流，最大速度达到-0.4 m/s，且边界层处逆流速度更大。0.1 s时，入口中心处流动变为正向流动，边界层依然为逆流。0.115 s时，中心处流动为逆向流动。0.125 s时，中心处流动为正向流动。0.2 s时，入口处流动速度趋于0。分析可知，中心处流动出现正向流动和逆向流动交替出现的现象，这和压力波的传递有关。中心处速度的绝对值在逐渐减小，到0.2 s时，流动速度趋于0。从0.085 s开始，边界层流动一直为逆向流动，流动速度与中心处流动速度和方向有关，中心处正向流动时，边界层流速较小，中心处速度越大，边界层流速越小；中心处逆向流动时，边界层流速较大，中心处逆流速度越大，边界层流速越大。

图6 0.05 s时入口速度分布图Fig.6 Velocity distribution of inlet at 0.05 s

图8为工况1条件下，考虑流固耦合的水击仿真和不考虑流固耦合的CFD水击仿真水击压强变化曲线。从图中可以看出，考虑流固耦合仿真结果的峰值压力比不考虑流固耦合的水击峰值压力小3.1%。这是因为在水击发生过程中，由于流体压力的增加，管路截面积变大，管壁变形吸收了一部分水击能量，使得水击峰值压力减小。

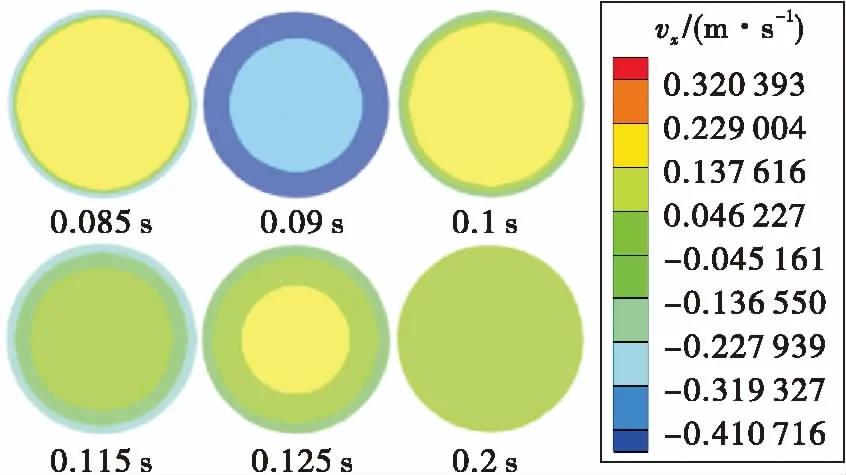
图7 不同时刻入口速度分布图Fig.7 Velocity distribution of inlet at different time

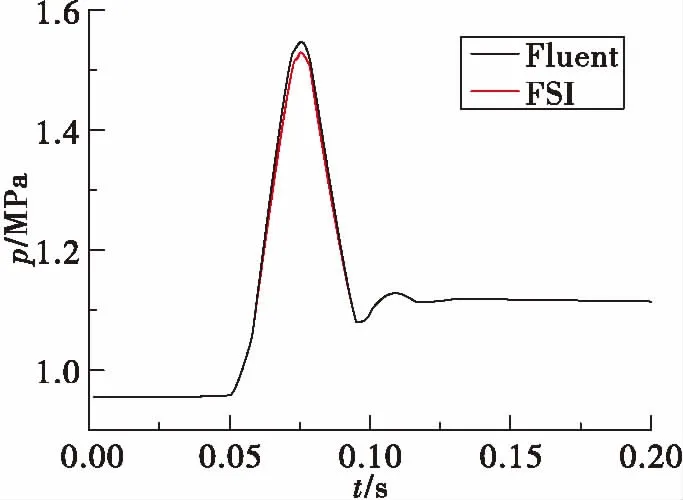
图8 CFD和FSI计算方法水击压强变化曲线Fig.8 Water hammer pressure at CFD and FSI

综合上述分析，水击的能量耗散主要有以下几种：通过动能和压力能的方式从入口逆流出管路；流体的粘性损失；通过结构的变形吸收能量。由图5、图7中可知，入口处压力一直处于较低水平，且入口处逆流速度很小，因此只有很少一部分水击能量通过动能和压力能的方式从入口逆流出管路。而结构吸收的能量使水击压力减小了3.1%，因此可以认为大部分水击能量的耗散是由于流体的粘性损失。从图5、图7可以看出：在压力下降过程中，管内出现了涡流，且压力下降到最低时，涡流最大；管壁附近一直为逆流，且逆流速度相对中心处较高。因此，通过涡流和壁面处摩擦导致的黏性损失较大，是水击能量耗散的主要原因。

图9为不同流量下水击压强变化曲线，从0.05 s阀芯作动开始，压强开始急剧增加，在0.075 s时压力达到峰值压力，0.096 s时压力达到最低值，经过两次的振荡达到稳态。不同流量的水击变化趋势一致，衰减速率和频率一致，水击的峰值压力随流量的增大而增大。

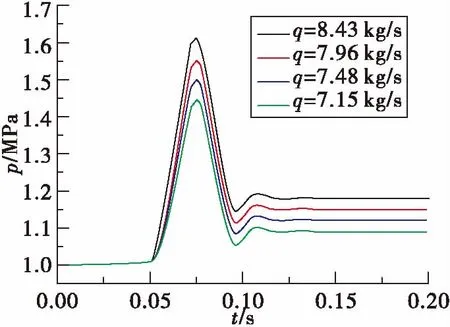
图9 不同流量下水击压强变化曲线Fig.9 Water hammer pressure at different mass flow rate

水击的峰值压力与流量的关系图如图10所示，峰值压力的变化和流量呈一次函数关系。水击峰值压力计算公式为：

(13)

式中：ρ为液体密度；a为声速；u为流动速度；T为水击周期；t为阀门关闭时间。

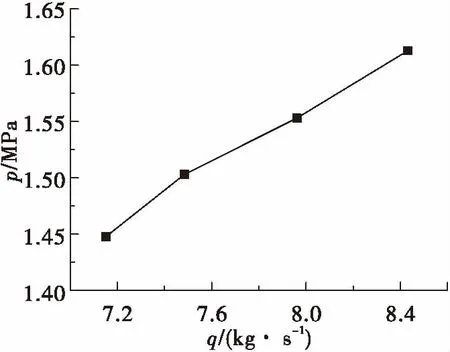
图10 峰值压力与流量关系图Fig.10 Relationship between pressure and mass flow rate

水击峰值压力与流速成正比，与仿真结果一致。

阀门关闭时间是影响水击特性的关键因素，图11为不同阀门关闭时间下水击压强变化曲线。在阀门关闭时间为0.02 s条件下，0.05 s时阀芯开始作动，0.065 s时压力达到峰值压力，之后阀门压力急剧降低，0.078 s时压力达到最小值，经过2.5个周期后压力趋于稳态值。在阀门关闭时间为0.04 s条件下， 0.075 s时压力达到峰值压力，之后阀门压力急剧降低，0.098 s时压力达到最小值，经过2个周期后压力趋于稳态值。在阀门关闭时间为0.06 s条件下， 0.085 s时压力达到峰值压力，之后阀门压力急剧降低，0.122 s时压力达到最小值，经过1个周期后压力趋于稳态值。阀门关闭时间的缩短增加了峰值压力和水击频率，增加了衰减时间，对管路造成恶劣的影响。阀门关闭时间短，会使水击峰值压力急剧增加，水击频率增大，衰减速率变慢。图12表示峰值压力p与关阀时间的倒数1/t的关系，从图中可以看出，p与1/t呈一次函数关系，与式(13)相吻合。

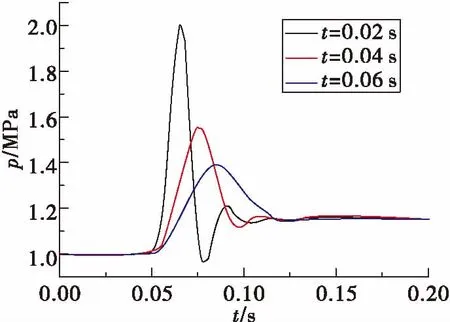
图11 不同关阀时间下水击压强变化曲线Fig.11 Water hammer pressure at different valve closure time

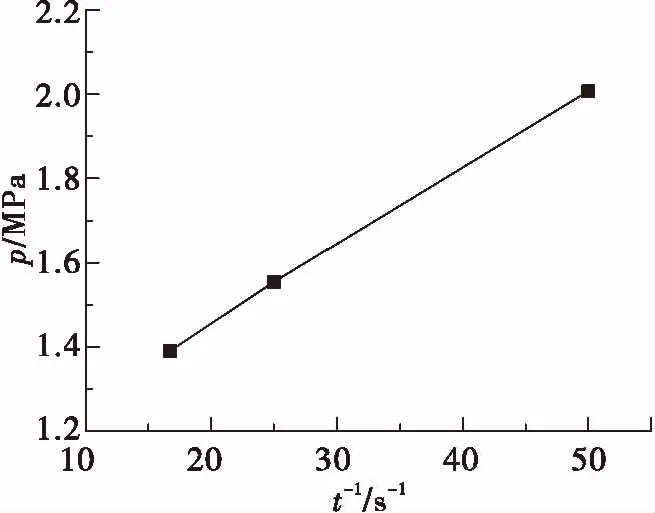
图12 峰值压力与关阀时间关系图Fig.12 Relationship between pressure and valve closure time

图13为不同背压对水击特性的影响，在流量、关阀时间等其他条件相同、背压不同的情况下，峰值压力、水击频率、衰减速率误差低于2%。因此，在进行轨控发动机高室压水力试验时，可以在保证流量和关阀时间情况下，减小出口背压，可以得出与高背压一致的水击压力变化曲线。

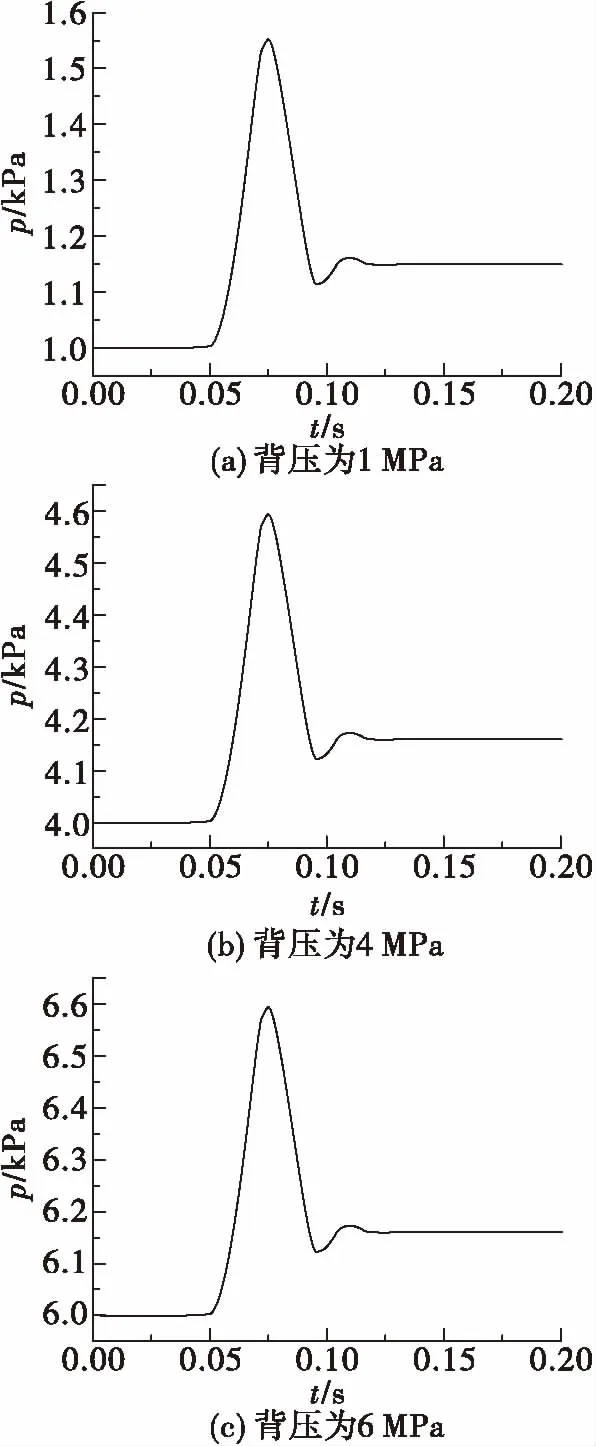
图13 不同背压下水击压强变化曲线Fig.13 Water hammer pressure at different backpressure

4 结论

利用基于流固耦合的数值模拟方法，对算例进行仿真。验证了使用Workbench15.0 平台构建双向流固耦合分析系统仿真的可行性。基于轨控发动机高室压、大流量、快响应的发展趋势，设计8组计算工况，分析了背压、流量、关阀时间对水击特性的影响，得到了以下结论：

1)Workbench15.0平台构建双向流固耦合分析系统不仅可以模拟水击发生过程中压力变化，还可以通过压力和流线的分布图分析压力波的传播过程和能量的耗散过程。

2)水击的能量只有很少一部分通过动能和压力能的方式从入口逆流出管路和通过结构的变形吸收能量这两种方式耗散。大部分水击能量的耗散是由于流体的粘性损失。粘性损失主要有涡流和壁面处摩擦两种方式。

3)流量是影响水击峰值压力关键因素，在管路截面积不变的情况下，流量越大，水击峰值压力越大，且流量与水击峰值压力呈一次函数关系。流量对水击频率和衰减速率没有影响。阀门关闭时间的缩短增加了峰值压力和水击频率，增加了衰减时间，对管路造成恶劣的影响。峰值压力p与关阀时间的倒数1/t呈一次函数关系。

4)在流量、关阀时间等其他条件相同、背压不同的情况下，峰值压力、水击频率、衰减速率误差低于2%。因此，在进行轨控发动机高室压水力试验时，在保证流量和关阀时间情况下，减小出口背压，可以得出与高背压较为一致的水击压力变化曲线。

对于更为复杂的轨控发动机管路系统，基于流固耦合的三维水击数值仿真不仅可以得出水击压力的变化，还可以得出水击发生过程中流动过程和水击波的传递过程。同时，三维仿真不需要对分支管路、弯管、变截面管路、异型截面管路进行简化，更加保证了仿真的准确性。本文作为前期工作，为基于流固耦合的水击仿真方法在复杂管路系统中的应用提供了参考。